BAB 4 HASIL DAN PEMBAHASAN. mahasiswa lulusan yang berasal dari School of Computer Science BINUS. datanya adalah seperti yang tertera pada Tabel 4.1.

(1)

BAB 4

HASIL DAN PEMBAHASAN 4.1 Hasil Analisis Data dan Pembahasan

Jumlah keseluruhan data yang peneliti peroleh adalah sebanyak 718 data

mahasiswa lulusan yang berasal dari School of Computer Science BINUS

UNIVERSITY. Dari 718 mahasiswa yang lulus pada tahun 2011 tersebut,

seluruhnya akan peneliti gunakan di dalam penelitian ini. Adapun bentuk

datanya adalah seperti yang tertera pada Tabel 4.1.

Tabel 4.1 Data Mahasiswa Lulusan

No. Jenis Kelamin Usia IPK Status Bekerja

1 L 21 2.77 0 2 P 21 2.78 0 3 L 21 3.03 0 : : : : : : : : : : : : : : : 716 L 23 3.04 1 717 L 23 3.21 1 718 P 25 3.68 1

Sebagai keterangan, untuk data jenis kelamin, ‘L’ mewakili laki-laki, dan

‘P’ mewakili perempuan. Untuk data usia menggunakan satuan tahun. Untuk

data status bekerja, ‘0’ mewakili belum bekerja, dan ‘1’ mewakili sudah bekerja.

(2)

Beberapa deskriptif data dari data-data yang telah diperoleh pada

penelitian ini ditunjukkan dalam Tabel 4.2 dan penyajian dalam bentuk

diagramnya diberikan dalam Gambar 4.1.

Tabel 4.2 Deskriptif Data Penelitian

Data Status Jumlah

Laki-laki Bekerja 126

Tidak Bekerja 60

Perempuan Bekerja 386

Tidak Bekerja 146

Usia ≤ 23 Tahun Bekerja 478 Tidak Bekerja 188

Usia > 23 Tahun Bekerja 34 Tidak Bekerja 18 IPK < 3.00 Bekerja 105 Tidak Bekerja 75 IPK ≥ 3.00 Bekerja 407 Tidak Bekerja 131

(3)

Data-data mahasiswa lulusan dalam bentuk variabel-variabel yang akan

digunakan di dalam pembentukan persamaan regresi logistik adalah seperti yang

ditunjukkan pada Tabel 4.3.

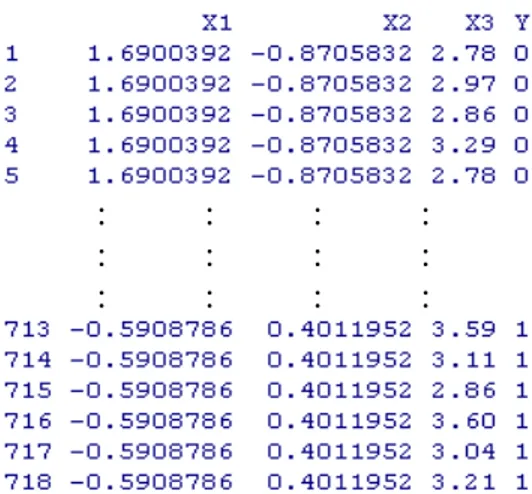
Tabel 4.3 Data Mahasiswa Lulusan Dalam Bentuk Variabel No. X1 X2 X3 Y 1 0 21 2.77 0 2 1 21 2.78 0 3 0 21 3.03 0 : : : : : : : : : : : : : : : 716 0 23 3.04 1 717 0 23 3.21 1 718 1 25 3.68 1

Variabel-variabel X1, X2, dan X3 merupakan variabel bebas, yang

berturut-turut mewakili jenis kelamin, usia, dan IPK dari setiap mahasiswa

lulusan. Dalam hal ini, nilai dari variabel X1 harus diubah agar dapat diproses di

dalam perhitungan, yaitu menjadi ‘0’ untuk laki-laki, dan ‘1’ untuk perempuan.

Variabel Y merupakan variabel tak bebas, yang mewakili status bekerja dari

setiap mahasiswa lulusan.

Adapun data yang diperoleh peneliti disimpan di dalam program

Microsoft Excel, dengan nama Data.xls. Agar dapat diproses menggunakan

Bahasa R, terlebih dahulu data tersebut harus dikonversikan ke dalam bentuk file

(4)

program R data tersebut harus diimpor terlebih dahulu dan dimasukkan ke dalam

sebuah variabel bernama data, menggunakan sintaks berikut ini.

data <- read.delim("Direktori Data")

Setelah direktori data ditentukan, maka sintaks tersebut akan menjadi seperti

sintaks di bawah ini.

data <- read.delim("d:/My Documents/Data.txt")

Pada saat mengimpor data ke dalam program R, sintaks read.delim yang

digunakan, karena data-data yang terdapat di dalam Data.txt dipisahkan oleh

spasi. Adapun isi dari variabel data setelah data-data selesai diimpor adalah

sebagaimana yang ditunjukkan di dalam Gambar 4.2.

: : : : : :

Gambar 4.2 Isi Variabel data

Call:

glm(formula = Y ~ X1 + X2 + X3, family = binomial)

Deviance Residuals:

Min 1Q Median 3Q Max -2.0077 -1.3491 0.7111 0.8618 1.2422

(5)

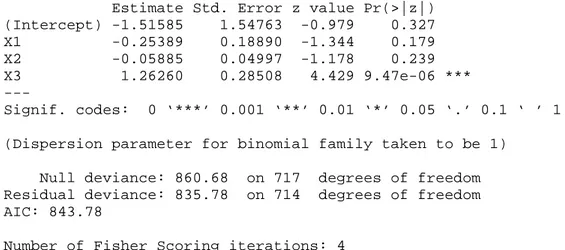
Estimate Std. Error z value Pr(>|z|) (Intercept) -1.51585 1.54763 -0.979 0.327 X1 -0.25389 0.18890 -1.344 0.179 X2 -0.05885 0.04997 -1.178 0.239 X3 1.26260 0.28508 4.429 9.47e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

Null deviance: 860.68 on 717 degrees of freedom Residual deviance: 835.78 on 714 degrees of freedom AIC: 843.78

Number of Fisher Scoring iterations: 4

Gambar 4.3Output Model Regresi Logistik Dengan Program R

Gambar 4.3 menunjukkan bahwa sesuai dengan nilai Pr(>|z|) yang dimiliki oleh

setiap variabel, maka variabel IPK (X3) signifikan, sedangkan kedua variabel

bebas lainnya, yaitu jenis kelamin (X1) dan usia (X2), tidak signifikan. Untuk

mengatasi masalah yang terjadi, maka peneliti mencoba untuk melakukan

standarisasi/normalisasi terhadap variabel jenis kelamin (X1) dan usia (X2). Adapun metode normalisasi yang peneliti gunakan adalah dengan menggantikan

nilai setiap pengamatan pada kedua variabel tersebut dengan sebuah nilai yang

baru, mengikuti Persamaan 4.1.

' x x μ σ − = (4.1)

Adapun x merupakan nilai pengamatan yang lama, μ merupakan nilai rata-rata, dan σ merupakan nilai simpangan baku dari populasi suatu variabel. Tampilan data setelah dilakukan normalisasi dan diimpor ke dalam program R adalah

(6)

: : : : : : : : : : : :

Gambar 4.4 Isi Variabel data Setelah Dilakukan Normalisasi

Selanjutnya, kembali peneliti akan melakukan pengolahan data untuk

memperoleh model regresi logistik dari data-data yang telah dinormalisasi

tersebut.

Call:

Deviance Residuals:

Min 1Q Median 3Q Max -2.0077 -1.3491 0.7111 0.8618 1.2422

Coefficients:

Estimate Std. Error z value Pr(>|z|) (Intercept) -3.15186 0.91476 -3.446 0.00057 *** X1 -0.11131 0.08282 -1.344 0.17893 X2 -0.09254 0.07858 -1.178 0.23891 X3 1.26260 0.28508 4.429 9.47e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(7)

Gambar 4.5 menunjukkan, bahwa setelah dilakukan normalisasi pun kedua

variabel tersebut (jenis kelamin dan usia) masih juga tidak signifikan. Pada

akhirnya, peneliti memutuskan untuk membuang dan tidak lagi

mengikutsertakan variabel jenis kelamin (X1) dan usia (X2) di dalam

proses-proses analisis selanjutnya. Hal ini menyisakan hanya satu buah variabel bebas,

yaitu IPK (X3), yang akan digunakan di dalam persamaan logit.

Call:

glm(formula = Y ~ X3, family = binomial)

Deviance Residuals:

Min 1Q Median 3Q Max -1.9770 -1.3650 0.7133 0.8687 1.0471

Coefficients:

Estimate Std. Error z value Pr(>|z|) (Intercept) -3.2540 0.9091 -3.579 0.000344 *** X3 1.2930 0.2834 4.562 5.06e-06 *** ---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Gambar 4.6Output Model Regresi Logistik Dengan Satu Variabel Bebas

Menurut Gambar 4.6, dikarenakan seluruh nilai variabel regresi logistik sudah

signifikan, maka dapat ditentukan persamaan logit (Persamaan 4.2) yang akan

peneliti gunakan di dalam proses analisis selanjutnya, sebagai berikut.

3 ( ) 3.2540 1.2930

g x = − + ⋅X

(8)

Kita juga dapat mengetahui odds ratios dari variabel IPK (X3), yaitu dengan

mengeksponenkan nilai koefisien X3, sehingga diperoleh hasil e1.293 =3.6437. Ini berarti, untuk setiap kenaikan satu unit nilai IPK, diharapkan kesempatan

(odds) untuk memperoleh pekerjaan akan meningkat sebesar 3.6437 kali

(264.37%). Dengan demikian, nilai peluang seorang mahasiswa lulusan baru untuk dapat memperoleh pekerjaan pun telah dapat ditentukan, yaitu dengan

menggunakan Persamaan 4.3. 3 3 3.2540 1.2930 3.2540 1.2930

( )

1

X X

e

x

e

π

=

− ₋ + ₊ ⋅ _⋅

+

_(4.3)

Sebagai analisis tambahan, peneliti juga hendak meneliti besarnya

peluang seorang mahasiswa lulusan baru untuk memperoleh gaji di atas empat

juta rupiah pada saat bekerja, apabila diketahui data-data jenis kelamin, usia, dan

IPK dari mahasiswa tersebut. Dalam hal ini, variabel tak bebas (Y)

dikelompokkan ke dalam dua kategori, yaitu gaji di bawah empat juta (0) dan

gaji di atas empat juta (1). Untuk variabel bebas, di antaranya adalah jenis

kelamin (X1), usia (X2), dan IPK (X3). Data-data dari 497 mahasiswa lulusan setelah diimpor ke dalam program R, tampak seperti Gambar 4.7.

(9)

: : : : : : : : :

Gambar 4.7 Data Mahasiswa Lulusan

Proses untuk memperoleh model regresi logistik sama persis dengan yang telah

dilakukan sebelumnya. Hasil analisis data ditunjukkan oleh Gambar 4.8.

Call:

Deviance Residuals:

Min 1Q Median 3Q Max -1.1668 -0.7009 -0.5521 -0.4107 2.4251

Coefficients:

Estimate Std. Error z value Pr(>|z|) (Intercept) -3.1440 3.1517 -0.998 0.3185 X1 -0.6173 0.2964 -2.082 0.0373 * X2 -0.1492 0.1250 -1.194 0.2324 X3 1.7525 0.3774 4.644 3.42e-06 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Gambar 4.8Output Model Regresi Logistik Dengan Program R

Gambar 4.8 menunjukkan bahwa sesuai dengan nilai Pr(>|z|) yang

(10)

signifikan, sedangkan variabel bebas lainnya, yaitu usia (X2), tidak signifikan.

Untuk mengatasi masalah ini, maka peneliti memutuskan untuk membuang dan

tidak lagi mengikutsertakan variabel usia (X2) di dalam proses-proses analisis selanjutnya. Hal ini menyisakan dua buah variabel bebas, yaitu jenis kelamin

(X1) dan IPK (X3), yang akan digunakan di dalam persamaan logit.

Call:

glm(formula = Y ~ factor(X1) + X3, family = binomial)

Deviance Residuals:

Min 1Q Median 3Q Max -1.1462 -0.6924 -0.5470 -0.4342 2.3758

Coefficients:

Estimate Std. Error z value Pr(>|z|) (Intercept) -7.1999 1.2763 -5.641 1.69e-08 *** X1 -0.5796 0.2948 -1.966 0.0493 * X3 1.7860 0.3763 4.746 2.07e-06 *** ---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Null deviance: 499.06 on 496 degrees of freedom Residual deviance: 471.00 on 494 degrees of freedom AIC: 477

Gambar 4.9Output Model Regresi Logistik Dengan Dua Variabel Bebas

Menurut Gambar 4.9, dikarenakan seluruh nilai variabel regresi logistik sudah

signifikan, maka dapat ditentukan persamaan logit (Persamaan 4.4) yang akan

peneliti gunakan di dalam proses analisis selanjutnya, sebagai berikut.

1 3

( ) 7.1999 0.5796 1.7860

g x = − − ⋅X + ⋅X

(4.4)

Untuk mengetahui odds ratio dari variabel jenis kelamin (X1), terlebih dahulu

(11)

Tabel 4.4 Tabel Kontingensi Antara Besarnya Gaji dan Jenis Kelamin Laki-laki Perempuan

Gaji < 4 Juta 291 106

Gaji ≥ 4 Juta 83 17

Dari tabel di atas dapat ditentukan odds ratio antara laki-laki dan perempuan,

yaitu 83 17 1.7785

291 106= . Ini berarti, mahasiswa lulusan yang berjenis kelamin laki-laki memiliki kesempatan (odds) untuk memperoleh gaji di atas empat juta

rupiah 1.7785 kali (77.85%) lebih besar dibandingkan mahasiswa lulusan yang berjenis kelamin perempuan. Untuk variabel IPK (X3), dengan mengeksponenkan koesifiennya, maka akan diperoleh 1.786

5.9655

e = . Ini berarti, jika variabel jenis kelamin dibiarkan tetap, maka untuk setiap kenaikan satu unit

nilai IPK, diharapkan kesempatan (odds) untuk memperoleh gaji di atas empat

juta rupiah akan meningkat sebesar 5.9655 kali (496.55%). Dengan demikian, nilai peluang seorang mahasiswa lulusan baru untuk dapat memperoleh gaji di

atas empat juta rupiah pun telah dapat ditentukan, yaitu dengan menggunakan

Persamaan 4.5. 1 3 1 3 7.1999 0.5796 1.7860 7.1999 0.5796 1.7860

( )

1

X X X X

e

x

e

π

=

− ₋ − ₋ ⋅ +_{⋅ +} ⋅ _⋅

+

_(4.5)

4.2 Uji Coba Program Aplikasi

Seperti yang telah peneliti utarakan sebelumnya, dikarenakan hanya

(12)

dirancang, peluang memperoleh pekerjaan hanya akan ditentukan oleh besarnya

IPK yang dimiliki oleh seorang mahasiswa, sedangkan peluang memperoleh gaji

di atas empat juta rupiah akan ditentukan oleh besarnya IPK dan jenis kelamin

dari mahasiswa tersebut.

Gambar 4.10 Tampilan Halaman Awal

Gambar 4.11 Tampilan Submenu “File”

Gambar 4.10 dan 4.11 merupakan tampilan halaman awal program, yang berada

(13)

“Open”, yang dapat digunakan oleh pengguna untuk memasukkan data dari file

teks yang diinginkan.

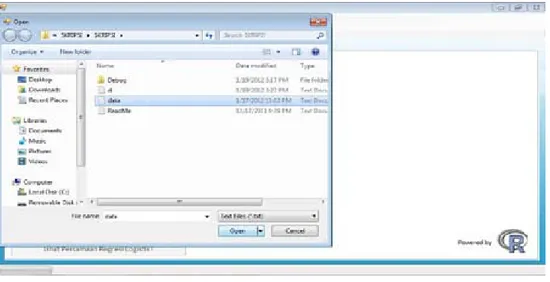
Gambar 4.12 Tampilan Saat Pengguna Memilih File Yang Akan Dimasukkan

Gambar 4.12 merupakan tampilan kotak dialog yang muncul pada saat pengguna

hendak memilih file yang akan dimasukkan. File yang dapat dimasukkan

hanyalah file berjenis teks yang berekstensi “.txt”.

(14)

Gambar 4.13 menunjukkan hasil analisis yang dilakukan terhadap data yang

telah dimasukkan. Hasil yang ditampilkan adalah nilai koefisien dan

nilai-nilai Z bagi variabel konstan (intercept), jenis kelamin (X1), dan IPK (X2).

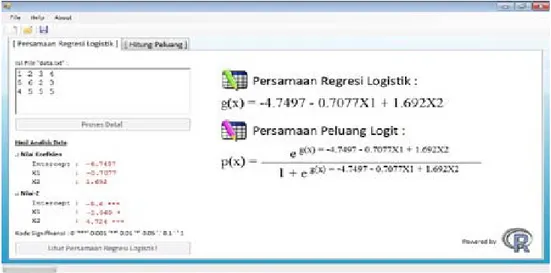
Gambar 4.14 Tampilan Setelah Tombol “Lihat Persamaan Regresi Logistik!” Ditekan

Setelah tombol “Lihat Persamaan Regresi Logistik!” ditekan, maka akan muncul

Persamaan Regresi Logistik dan Persamaan Peluang Logit, seperti yang dapat

dilihat pada Gambar 4.14 di atas.

(15)

Gambar 4.15 merupakan tampilan halaman menu “Hitung Peluang”. Pengguna

diminta untuk memasukkan besarnya IPK dan memilih jenis kelamin yang

dikehendaki.

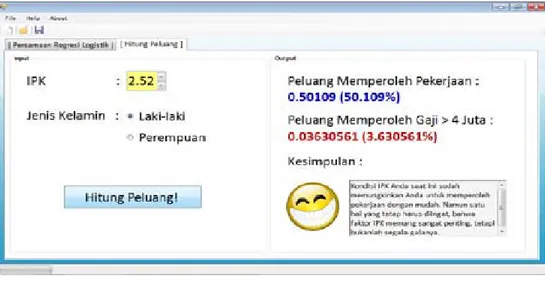
Gambar 4.16 Tampilan Setelah Tombol “Hitung Peluang!” Ditekan

Setelah tombol “Hitung Peluang!” ditekan, maka akan muncul nilai Peluang

Memperoleh Pekerjaan, nilai Peluang Memperoleh Gaji > 4 juta, dan

kesimpulan mengenai kondisi peluang dari mahasiswa yang bersangkutan.

Adapun kesimpulan yang diberikan dibedakan menjadi dua bagian, yaitu untuk

presentase Peluang Memperoleh Pekerjaan kurang dari 50% dan untuk

(16)

Gambar 4.17 Tampilan Setelah Tombol “Hitung Peluang!” Ditekan

Gambar 4.17 merupakan tampilan halaman menu “Hitung Peluang”, ketika

presentase Peluang Memperoleh Pekerjaan lebih dari atau sama dengan 50%.

Adapun hasil-hasil tersebut dapat diinterpretasikan sebagai berikut.

Apabila seorang mahasiswa laki-laki lulus dengan IPK sebesar 2.52, maka diperkirakan peluang mahasiswa tersebut untuk dapat memperoleh pekerjaan adalah sebesar 0.5011 atau 50.11%, dan peluangnya untuk memperoleh gaji di atas empat juta rupiah pada saat bekerja adalah sebesar 0.0363 atau 3.63%.

(17)

Gambar 4.18 Tampilan Saat Pengguna Menyimpan Hasil Analisis Data

Pengguna juga dapat menyimpan hasil analisis data yang telah dilakukan.

Program akan menuliskan dan menyimpan seluruh hasil analisis data ke dalam

sebuah file teks yang diinginkan oleh pengguna, sebagaimana ditunjukkan pada

Gambar 4.18 di atas.

4.3 Usulan/Kondisi Yang Mendukung Hipotesis

Hipotesis atau jawaban sementara dari perumusan masalah yang

ditetapkan oleh peneliti, adalah sebagai berikut.

H0 : Besarnya peluang memperoleh pekerjaan tidak dipengaruhi oleh

seluruh atau sebagian dari ketiga faktor IPK, jenis kelamin, dan usia.

H1: Besarnya peluang memperoleh pekerjaan dipengaruhi oleh

seluruh atau sebagian dari ketiga faktor IPK, jenis kelamin, dan usia.

(18)

Dari hasil analisis data yang telah peneliti lakukan dan paparkan pada bagian

sebelumnya, dapat diketahui bahwa peluang seorang mahasiswa lulusan baru

dalam memperoleh pekerjaan dipengaruhi oleh sebuah faktor, yaitu IPK. Hal ini

menjadikan hipotesis nol di atas harus ditolak, dan dapat disimpulkan bahwa

besarnya peluang memperoleh pekerjaan dipengaruhi oleh faktor IPK dari seorang mahasiswa lulusan baru.

Sesuai dengan manfaat penelitian ini (bagi mahasiswa aktif), yang telah

peneliti sampaikan sebelumnya, dan bagi pihak manapun yang membaca hasil

penelitian ini, telah dapat dipastikan bahwa nilai Indeks Prestasi Kumulatif

(IPK) merupakan sebuah faktor yang paling berpengaruh di dalam menentukan

besar-kecilnya peluang seorang mahasiswa baru di dalam memperoleh

pekerjaan. Meskipun pada kenyataannya IPK bukanlah segala-galanya dan

bukan satu-satunya faktor yang menentukan keberhasilan seseorang di dalam

memperoleh pekerjaan, namun tidak dapat dipungkiri bahwa IPK tetap

memegang peranan yang terpenting jika menyangkut masalah pencarian

pekerjaan, karena hal tersebut telah teruji dan terbukti dengan pasti secara

statistik di dalam penelitian ini.

Menurut data mahasiswa lulusan yang peneliti peroleh, dari keseluruhan

mahasiswa lulusan yang memiliki gaji dengan nominal tertinggi (lebih dari atau

sama dengan enam juta rupiah), 58.82% atau lebih dari setengahnya berprofesi sebagai wirausahawan/wati (entrepreneur). Maka, sangatlah baik apabila

seorang mahasiswa aktif memiliki rencana untuk memulai kegiatan wirausaha.

(19)

dijalankan, tidak hanya pada saat telah lulus dari bangku kuliah, tetapi juga