INTERFERENSI DAN DIFRAKSI
Mata Kuliah: Gelombang & Optik
Dosen: Andhy Setiawan
DIFRAKSI
CELAH TUNGGAL DAN KISI
B. Difraksi
•
Difraksi
merupakan
gejala
pembelokan
(penyebaran) gelombang
ketika menjalar
melalui celah sempit atau tepi tajam suatu
Benda.
Benda.
•
Difraksi terjadi bila ukuran celah lebih kecil dari
panjang gelombang yang melaluinya.
Teori yang mendasari gejala difraksi
Prinsip Huygens-Fresnel:
Dalam proses perambatan gelombang bebas,
setiap titik pada suatu muka gelombang
berfungsi sebagai sumber sekunder sferis
berfungsi sebagai sumber sekunder sferis
untuk anak gelombang (wavelet), dengan
frekuensi yang sama dengan gelombang
primernya.
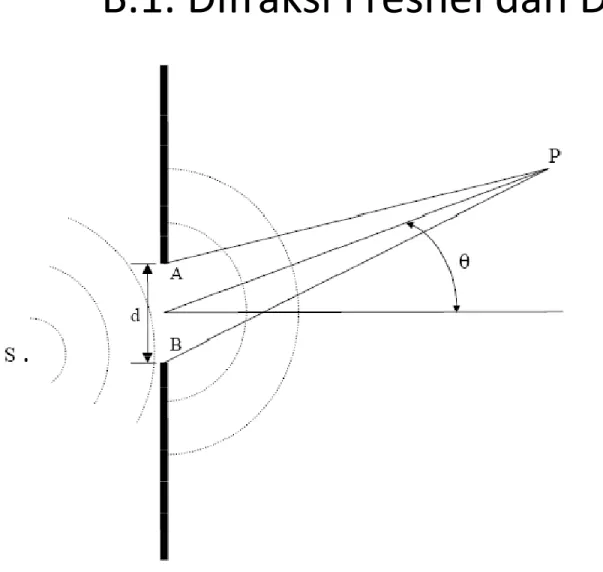
B.1. Difraksi Fresnel dan Difraksi Fraunhofer
•Menurut prinsip Huygens-Fresnel titik A dan B pada tepi celah,
merupakan sumber sekunder dengan fase yang sama.
•Efek difraksi diamati pada sutu titik P pada arah θ terhadap sumbu celah. Difraksi Fresnel: jika titik P dan
sumber gelombang datang tidak sumber gelombang datang tidak begitu jauh dari celah, sehingga gelombang datang tidak dapat
dianggap sebagai gelombang datar. •Difraksi Fraunhofer: jika titik P dan sumber gelombang datang cukup jauh dari celah, sehingga gelombang datang dapat dianggap sebagai
gelombang datar. Gambar gejala difraksi dari suatu gelombang datar
Difraksi Celah Tunggal: Difraksi Fraunhofer
•
gelombang datang berupa gelombang datar
•
jartak titik P ke celah, jauh lebih besar dari
lebar celah, r >> d .
lebar celah, r >> d .
Difraksi gelombang datang berupa gelombang datar
•Titik-titik pada celah antara A dan B, dapat dipandang sebagai sumber-sumber gelombang sekunder.
•Jadi Pola difraksi celah ini, dapat didekati sebagai pola interferensi sistim banyak celah sempit, masing-masing berjarak a.
Apabila fungsi gelombang yang berasal dari celah sempit pertama (celah sempit paling atas dititk A) adalah:
Misalkan:
E
=
E
e
−iωt 0 1(
)
(
ω 1 sinθ)
0 a n k t i nE
e
E
=
− − −Sehingga di titik P akan terjadi superposisi dari
E
1,
E
2,
E
3,...,
E
n∑
=
+
+
+
+
=
E
E
E
E
nE
E
...
=
−∑
( )
− N n ika t ie
e
E
E
0 ω 1 sinθ∑
==
+
+
+
+
=
n n nE
E
E
E
E
E
1 3 2 1...
t ie
E
E
=
0 − ω+
E
0e
−i(
ωt−kasinθ)
+
E
0e
−i(
ωt−2kasinθ)
+
...
+
E
0e
−i(
ωt−k(
N−1)
asinθ)
(
)
(
θ θ θ)
ω sin 2 sin 1 sin
0
1
...
− −+
+
+
+
=
i t ika ia ika Ne
e
e
e
E
E
∑
==
ne
e
E
E
1 01
1
1
1
sin sin−
−
=
−
−
=
n ikaNika θθ Ne
e
r
r
S
− − −
−
=
θ θθ
θ
θ
θ
sin 2 sin 2 sin 2 sin 2 sin 2 sin 2 ka i ka i e e ka i N ika N ika N ika Ne
e
e
e
S
θ
sin
sin
2
i
ka
N
kae
(
)
(
)
=
=
− −θ
θ
θ
θ
θ θsin
2
sin
sin
2
sin
sin
2
sin
2
sin
2
sin
2
sin 1 2 sin 1 2ka
N
ka
e
ka
i
ka
i
e
S
N ka i N ka i NMaka persamaan ..1 berubah menjadi:
(
)
=
− −θ
θ
θ ωsin
2
sin
sin
2
sin
sin 1 2 0ka
N
ka
e
e
E
E
N ka i t i(
)
=
− + −θ
θ
θ
ω
sin
2
1
sin
sin
2
1
sin
sin 1 2 1 0ka
kaN
e
E
E
i t ika NKemudian bila jumlah sempit N diperbanyak sehingga menuju tak hingga, maka
N
ka
N
kb
e
E
E
i t ikb
=
− +θ
θ
θ ωsin
1
sin
sin
2
1
sin
sin 2 1 0(
N
−
1
)
a
=
b
misalnya(
N
−
1
)
a
≅
Na
=
b
ka
N
θ
sin
2
1
sin
θ
θ
sin
2
1
sin
2
1
sin
ka
≈
ka
karenaN
kb
kb
e
E
E
i t ikb
=
− +θ
θ
θ ωsin
2
1
sin
2
1
sin
sin 2 1 0θ
sin
2
1
b
r
=
misal( )
[
]
N
kr
kr
e
E
E
=
0 −iωt+ikr
sin
N
kb
kb
e
E
E
i t ikb
=
− +θ
θ
θ ωsin
2
1
sin
2
1
sin
sin 2 1 0kr
0θ
β
=
kr
=
21kb
sin
Jika Maka :(
)
N
e
E
E
i t
=
− −β
β
β ωsin
0(
)
N
e
E
E
i t kr
=
− −β
β
ωsin
0Superposisi gelombang di titik P
Maka pola difraksinya dapat diperoleh melalui Intensitas gelombang dititik P 2 2 0
sin
N
I
I
=
β
β
Untuk θ = 0 diperoleh pucak intensitas maksimum sebesar ,
I
0 jadi intensitas maksimum terletak pada arah sumbu celah0
I
R
r
r
r
r
r
.
0=
xr
PUntuk bukaan (aperture) yang tidak berbentuk celah, misalnya bebentuk lingkaran dengan jari-jari R, maka :
(
sin
θ
,
0
.
cos
θ
)
0=
r
r
(
R
cos
ϕ
,
R
sin
ϕ
,.
0
)
R
=
r
R z yθ
ϕ
R0 0r
(
)
θ
π
R
e
ϕ θ ωRdRd
E
dE
=
02 −i kR cos sin − tθ
RdRd
dS
=
RdR
d
e
e
R
E
E
d ikR t i∫ ∫
=
− 0 2 0 cos sin 2 02
1
2
ω π θ ϕϕ
π
θ
ρ
=
kR
sin
Misal :θ
ρ
sin
k
R
=
dR
k
d
ρ
=
sin
θ
θ
ρ
sin
k
d
dR
=
θ
sin
k
(
)
2sin
θ
ρ
ρ
k
d
RdR
=
Subtitusikan ke persamaan …1 akan diperoleh persamaan
RdR
d
e
e
R
E
E
d i t i∫ ∫
=
− 0 2 0 cos 2 02
1
2
ω π ρ ϕϕ
π
(
)
∫ ∫
=
−ω θ π ρ ϕθ
ρ
ρ
ϕ
π
sin 0 2 2 0 cos 2 0sin
2
1
2
i t kd ik
d
d
e
e
R
E
E
(
)
∫
−=
ωρ
θρ
ρ
θ
sin 0 2 2 0)
(
sin
1
2
i t kdd
J
k
e
R
E
E
(
θ
)
ϕ
ρ
ρ
π
θ π ϕ ρ ωd
d
e
k
e
R
E
E
kd i t i∫ ∫
=
− sin 0 2 0 cos 2 2 0sin
1
2
1
2
(
θ
)
∫
0 0 2 2sin
k
R
Dengan menggunakan fungsi Bessel
( )
ϕ
π
ρ
π ρ ϕd
e
J
=
∫
i 2 0 cos 02
1
( )
θ
ρ
d
=
kd
sin
( )
ρ
=
1
2∫
π(
ϕ+ρ ϕ)
ϕ
(
)
∫
( )
−
=
ω
ρ
θ
ρ
ρ
θ
sin
0
0
2
2
0
sin
1
2
i
t
dk
d
J
k
e
R
E
E
θ
sin
Rk
u
=
( )
u
( )
J
( )
u
d
ρ
J
d u∫
=
0 0(
θ
)
( )
ρ
ρ
ρ
θ ωd
J
e
Rk
E
E
kd t i∫
−=
sin 0 0 2 0sin
1
2
( )
( )
ρ
ρ
θ ωud
J
e
u
E
E
kd t i∫
−=
2
01
2 sin 0∫
0( )
u
u
J
e
E
E
=
2
0 −iωtIntensitas pada arah θ adalah
( )
2 02
=
u
u
J
I
I
( )
u
e
J
( )
ρ
ud
ρ
E
E
=
∫
0 0 2 02
( )
u
J
e
u
E
E
=
2
01
−iωtKisi Difraksi
Kisi Difraksi merupakan sistem N buah celah, dengan lebar celah yang teratur. Diraksi oleh kisi seferti ini akan
menghasilkan pola difraksi tunggal tak sempit dengan pola interferensi N buah sumber yang sinkron.
r0 P b a θ
(
n
−
1 a
)
sin
( )
θ
rGambar 6.13 memperlihatkan difraksi oleh sebuah kisi, lebar celah dan jarak antara celah masing-masing b dan a. Bila kisi ini disinari cahaya monokromatik, osilasi listrik di titik P yang
ditimbulkan oleh celah ke nomor ke n adalah:
( )
=
− − −β
β
ωsin
0 t u kr i nE
e
E
β
0 n Dimana =−
+
=
−
=
∆
+
∆
=
−
=
∆
o o o or
a
n
r
r
a
n
r
r
r
r
r
r
r
θ
θ
sin
)
1
(
sin
)
1
(
n
E
E
E
E
E
=
1+
2+
3+
...
+
Yang memberikan hasil:)
(
1θ
∑
==
N n nE
E
) 0 ( 01sin
i kro u te
E
E
ωβ
β
− + − −
=
( ( ( 1) sin ) 01 ) sin ( ( 01sin
sin
i k ro a u t i k ro n a u te
E
e
E
θ ω θ ωβ
β
β
β
− + − − − + − − −
+
+
+
L
[
]
β
sin
ω[
θ θ]
β
β
( ) sin ( 1) sin 011
...
sin
i u t ikr ika i n kae
e
e
e
E
E
− − − o+
+
+
−
=
…..
1Dengan
e
ika sin ϑ1
1
sin sin−
−
=
−
−
=
r
ne
ikaNika θθS
………2
−
−
−
−
=
θ θθ
θ
θ
θ
sin 2 sin 2sin
2
sin
2
sin
2
sin
2
ka i ka ie
e
ka
i
N
ika
N
ika
N
ika
e
e
e
e
S
2
e
( )
=
−θ
θ
θsin
2
1
sin
sin
2
1
sin
sin 1 2 1ka
kaN
e
S
ika NUntuk lebar celah sempit a mendekati nol. Maka
(
N
−
1
)
a
=
Na
=
Nb
(
)
=
− − −β
β
ωsin
01 t u kr i oe
E
E
θ
θ
θsin
1
sin
sin
2
1
sin
sin 2 1kb
Nkb
e
ika
β
(
)
=
− − −β
β
ωsin
01 t u kr i oe
E
E
θ
sin
2
1
sin
kb
θ
θ
θsin
2
1
sin
sin
2
1
sin
sin 2 1kb
Nkb
e
ikbmisal
δ
=
kb
sin
θ
=
β
β
sin
01E
E
− −2
sin
2
sin
) (δ
δ
ω δN
e
i k t…..
2 sehingga 2 2
sin
=
NE
β
I
2sin
N
δ
2 1sin
=
β
β
oNE
I
2
sin
2
sin
δ
N
2 0sin
=
β
β
I
I
22
sin
2
sin
δ
δ
N
N
Intensitas maksimum utama (primer) dicapai bila
δ
=
m
π
2
m
m
kb
m
π
θ
π
θ
π
δ
=
=
=
2
sin
sin
2
1
2
dengan m bilangan bulat
b
m
b
m
kb
λ
θ
λ
π
π
θ
θ
=
=
=
sin
2
2
sin
sin
Maksimum tambahan (sekunder) dicapai apabila
π
δ
2
)
1
2
(
2
−
=
m
N
dengan2
,
1
±
±
=
m
Nb
m
m
kNb
π
θ
π
θ
)
1
2
(
sin
2
)
1
2
(
sin
2
1
+
=
+
=
Nb
Minimum (titik nol) terjadi bila
π
δ
m
N
=
2
denganm
=
±
1
,
±
2
Nb
m
m
kNb
λ
θ
π
θ
=
=
sin
sin
2
1
andhysetiawanApabila cahaya yang datang terdiri dari dua panjang gelombang yang
berbeda, maka kedudukan maksimum utama dari kedua panjang gelombang tersebut pada orde m yang sama akan terpisah bila