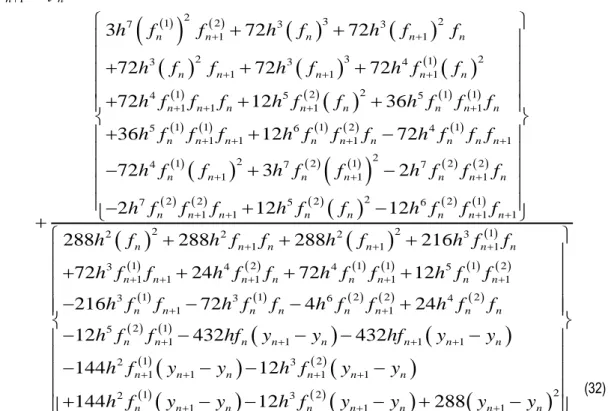La Zakaria dan Machudor Yusman

(1)

KONTRUKSI SKEMA IMPLISIT APROKSIMASI RASIONAL BERPENYEBUT

KUADRATIK UNTUK MENYELESAIKAN MASALAH NILAI AWAL SUATU

PERSAMAAN DIFERENSIAL BIASA ORDE PERTAMA

La Zakaria dan Machudor Yusman

Jurusan Matematika FMIPA, Universitas Lampung Jl. Prof. S. Brojonegoro No. 1 Bandar Lampung 35145

Email : airakaz_2k7@yahoo.com

Diterima 6 Juni 2007, perbaikan 24 September 2007, disetujui untuk diterbitkan 28 September 2007

ABSTRACT

For efficient and effective reasons, we use numerical method to solve an initial value problem (IVP) that given in the form of the first order differential equation. There are some schemes was constructed based on a rational or polynomial function form. Using the method of undetermined coefficients, it is easy to show that not only Euler’s method and Taylor’s method can be derived from a polynomial function but also the explicit rational approximation schemes. In this article we describe how to obtain an implicit rational approximation scheme to solve an IVP.

Keywords: Initial Value Problem, Implicit or Explicit Rational Approximation Scheme, The Method of Undetermined Coefficients

1. PENDAHULUAN

Dalam menyelesaikan suatu Masalah Nilai Awal suatu Persamaan Diferensial Biasa (MNAPDB) orde satu secara numerik tersedia banyak skema standar baik bentuk eksplisit maupun implisit1)_{. Beberapa diantaranya}

diturunkan dari asumsi solusi MNAPDB orde satu berbentuk fungsi polinomial (metode Euler dan metode Taylor, misalnya). Dalam asumsi fungsi solusi berbentuk fungsi rasional, Lambert dan Shawn telah memulainya2)_{. Keakuratan skema yang diturunkan}

Lambert dan Shawn memberikan hasil integrasi terhadap sebuah MNAPDB yang memiliki titik singularitas memberikan hasil berbeda signifikan dibandingkan dengan menggunakan metode Euler atau Taylor. Sungguhpun demikian, integrator-integrator yang dihasilkan dari asumsi fungsi solusi berbentuk fungsi polinomial atau rasional belum mampu mengatasi MNAPDB yang memiliki sifat kualitatif. Dengan kondisi ini, bermunculanlah sejumlah integrator-integrator geometris3,4,5)_{. Terlepas dari keakuratan dan efesiensi}

waktu proses integrasi, dalam artikel ini dipaparkan teknis menurunkan beberapa skema implisit untuk menyelesaikan MNAPDB orde satu dengan asumsi bentuk fungsi solusi MNAPDB yang dimaksud adalah fungsi rasional berpenyebut kuadratik. Sedangkan metode yang digunakan dalam mendapatkan skema yang dimaksud adalah dengan menggunakan eliminasi koefisien yang tak diketahui1,2,6)_{. Adapun alat yang}

digunakan untuk membantu mengeliminasi koefisien

1.1. MNAPDB Orde Pertama

Masalah Nilai Awal (MNA) dalam konteks persamaan diferensial biasa adalah sebuah masalah yang melibatkan satu fungsi

y





f

 

x

yang tidak diketahui beserta turunan-turunanya dalam sebuah persamaan yang memenuhi syarat awal yang diberikan. Bentuk umum MNA persamaan diferensial orde pertama adalah :

 

x

y

f

y





,

(1)

dengan syarat awal

 

x

0

y

0

y



(2)

dengan

y



= Turunan pertama dari fungsi real

y

 

x

 

x

y

f

,

= Suatu fungsi bernilai real dengan peubah x dan y

0

x

= Nilai awal x

0

y

= Nilai fungsi y(x) untuk

x



x

₀

Menyelesaikan MNA (1) – (2) dilakukan dengan mencari suatu fungsi

y

 

x

yang memenuhi persamaan diferensial biasa (1) beserta syarat awal (2). Dalam upaya menyelesaikan Persamaan (1) secara numerik umumnya hanya dilakukan dengan mencari nilai-nilai fungsi

y

_r yang mendekati solusi eksak

y

 

x

pada

(2)

1.2. Prinsip Polinomial Oskulasi

Polinomial oskulasi (Osculating Polynomial) adalah suatu fungsi pendekatan berbentuk polinomial yang nilai-nilainya tidak hanya cocok nilainya dengan sebuah fungsi yang diberikan pada titik-titik tertentu, tetapi juga pada titik-titik tertentu itupun turunan-turunan fungsi pendekatan polinomial hingga berderajat tertentu akan cocok dengan turunan-turunan fungsi yang diberikan7)_.

Dengan demikian, bila

p

 

x

merupakan suatu fungsi polinomial dan

y

 

x

merupakan fungsi sebenarnya maka polinomial oskulasi mengharuskan:

   

x

k

y

x

k

p



 

k

 

k

p x





y x





 n

_{ }

 n

_{ }

k k

p

x



y

x

dimana :

 

x

k

p

= Polinomial p(x) di x = xk

 

x

k

p

' = Turunan pertama dari p(x) di x = xk

 n

_{ }

k

p

x

= Turunan ke-n dari p(x) di x = xk

 

x

k

y

= Fungsi y(x) di x = xk

 

x

k

y

' = Turunan pertama dari y(x) di x = xk

 n

_{ }

k

y

x

= Turunan ke-n dari y(x) di x = xk 1.3. Bentuk Umum Fungsi Rasional

Fungsi Rasional adalah fungsi hasil bagi polinomial dengan polinomial. Misalkan

P

p

 

x

merupakan

polinomial berderajat p dan

Q

q

 

x

merupakan

polinomial berderajat q, maka fungsi

R

_pq

 

x

dinotasikan dengan

 

_{ }



    _q t t t p r r r q p pq x b x a x Q x P x R 0 0 (3) atau

 

_q q p p pq

x

b

x

b

x

b

x

a

x

a

x

a

x

R





...

2 2 1 0 2 2 1 0 dengan

Q

q

 

x



0

untuk

x



R

Persamaan (3) mempunyai koefisien-koefisien q

p

b

a

0

,

1

,...,

,

0

,

1

,...,

yang tidak diketahui

sebanyak

(p + q + 2) koefisien (4)

1.4. Metode Eliminasi Koefisien-koefisien yang Tak Diketahui

Metode eliminasi koefisien-koefisien yang tak diketahui digunakan untuk mendapatkan rumus selisih implisit yang digunakan untuk menyelesaikan persamaan diferensial.

Asumsikan solusi persamaan diferensial orde pertama

 

x

y

f

y





,

dengan syarat awal

 

x

0

y

0

y



Rumus pendekatan polinomial dapat diperoleh dari fungsi polinomial yang diberikan oleh Lambert & Shaw2)_,

 

_



4 0 s s s

x

a

x

F

,

x





x

n

,

x

n_₁



(5) Asumsikan bahwa

F

 

x

melalui titik



x

_n

,

y

_n



dan



x

n1

,

y

n1



dan asumsikan juga

 

_{ }

x

F

1 dan

 

_{ }

x

F

2 masing-masing melalui



x

_n

,

y

_n



dan



x

n1

,

y

n1



.

Dengan demikian

F

 

x

memenuhi persamaan berikut :

 

x

n j

y

n j

F

_



_  

 

j n j n

f

x

F

1 _



_  2

 

 1 j n j n

f

x

F

_



_ dimana :

1 ,

0 

j

j n

x



_  





j n j n j n

F

x

y

f

_



1 _

,

_    





j n j n n

F

x

y

f

_11



2 _

,

_ atau 4 4 3 3 2 2 1 0 n n n n n

a

x

a

x

a

x

a

x

y





(6) 4 1 4 3 1 3 2 1 2 1 1 0 1        n  n  n  n n a ax a x a x a x y (7) 3 4 2 3 2 1

2

n

3

n

4

n n

a

x

a

x

a

x

f





(8) 3 1 4 2 1 3 1 2 1 1

2



3



4

 





n



n



n n

a

x

a

x

a

x

f

(9)   2 4 3 2 1

12

6

2

_n _n n

a

x

a

x

f





(10)   2 1 4 1 3 2 1 1

2

6



12

 





n



n n

a

x

a

x

f

(11)

Dari keenam persamaan tersebut lima koefisien as, s =

0, 1, 2, 3, dan 4 yang tak diketahui, dieliminasi dengan cara sebagai berikut :

Persamaan (6) dan (7) dieliminasi koefisien

a

₀

(3)





_

_



 





1



2 1 2 4 1 2 1 2 3 1 2 1 1                 n n n n n n n n n n n n x x x x a x x x x a x x a a h y y (12) dimana :

h



x

_n_1



x

_n

a

₁

diperoleh :





_

_



1



2 1 2 4 1 3 2 2 1

2

3

2

   







n n n n n n n n n

x

a

x

a

h

f

h

y

(13 )

a

₁

diperoleh :





_

_



1



2 1 2 4 1 3 2 1 2 1 2 3 2               n n n n n n n n n x x x x a x x a a h f h y y (14) Persamaan (8) dan (9) dieliminasi koefisien

a

₁

diperoleh :





_

_



1



2 1 2 4 1 3 2 1

4

3

2

   







n n n n n n n n

x

a

x

a

h

f

(15) Persamaan (13) dan (15) dieliminasi koefisien

a

₂

diperoleh :



 





1



4 3 2 1 3 1

2

  









n n n n n n

x

a

h

f

h

y

(16) Persamaan (10) dan (11) dieliminasi koefisien

a

₂

diperoleh :    





_

_

1 4 3 1 1 1

12

6

_ 



_

_

n n n n

x

a

h

f

(17) Pada persamaan (16) dan (17) eliminasi koefisien

a

₃

dan

a

₄ diperoleh :



 





   



0 6 12 1 1 1 2 1 3 1       _ _ _ h f f h f f h y y_n _n _n _n _n _n ₍₁₈₎ atau







 1  1



1 2 1 1

12

2

n n n n n n

f

h

f

h

y

_





_





_



(19)

Persamaan (19) merupakan sebuah integrator bentuk implisit guna menyelesaikan masalah Nilai Awal (1) – (2).

2. METODE PENELITIAN

Guna mencapai tujuan penelitian ini telah digunakan pendekatan studi literatur dan praktik komputer. Adapun

sebagai berikut. Pertama dimulai dengan mendapatkan beberapa skema aproksimasi bentuk implisit berdasarkan fungsi berbentuk fungsi rasional dalam menyelesaikan MNA

y





f

 

x

,

y

dengan syarat awal

y

 

x

₀



y

₀. Kemudian mengimplementasi skema aproksimasi yang diperoleh untuk beberapa kasus MNA (1) – (2). Selanjutnya langkah terakhir, mengamati pertumbuhan galat yang dihasilkan oleh suatu metode terhadap penyelesaian MNA untuk kemudian dibandingkan.

3. HASIL DAN PEMBAHASAN

Pembentukan Skema Pendekatan Rasional Bentuk Implisit untuk Menyelesaikan MNAPDB Orde Pertama 3.1. Pendekatan Rasional Dengan Penyebut Fungsi Linier

Rumus pendekatan rasional yang dibentuk dengan cara pengeliminasian adalah skema pendekatan rasional dari fungsi rasional yang dikemukakan oleh Lambert & Shawn2)_{, sebagai berikut:}

 

x

b

x

a

x

R

P s s s







 0 0 ₍₂₀₎ dengan 0

b

x





p

a

dan

b

₀ adalah koefisien yang belum diketahui nilai-nilainya



0 ,

1 ,

2 ,

3 ,...

p



s

,

a

_s





,

1





x

n

x

n

x

, n = 0,1,2,3,…,N

Persamaan (20) memiliki koefisien yang tidak diketahui sebanyak

(p+3) koefisien (21) Dengan menggunakan prinsip polinomial oskulasi pada R(x)dalam interval



x

_n

,

x

_n_₁



maka dari persamaan (20) dengan mengambil

x



x

_n dan

x



x

_n_₁ pada R(x) dan turunan-turunannya diperoleh sistem persamaan berikut :





_

   





p s s n s n n

b

x

a

x

y

0 1 1 0 1





_





p s s n s n n

b

x

a

x

y

0 0





1 1 1 1 1 0 1        



 n p s s n s n n b x sa x y f





n p s s n s n n

b

x

sa

x

y

f









  1 1 0

(4)









1 2 2 1 1 0 ) 1 ( 1

1

2

     









n p s s n s n n

b

x

s

a

x

f









n p s s n s n n

b

x

s

a

x

f

1

2

2 2 0 ) 1 (









 











(1) 1 3 3 1 1 0 ) 2 ( 1 1 2 3        



   n p s s n s n n b x s s s a x f f











(1) 3 3 0 ) 2 ( ₁ ₂ ₃ n p s s n s n n b x s s s a x f f  



    





( 1) 1 1 0 ) ( 1

(

1 )

   



n







np p n

b

x

p

f





( 1) 0 ) (

)

1 (









p n n p n

b

x

p

f

(22) dengan 0 0

b

x





,...

3 ,

2 ,

1 

p

n

f

= nilai fungsi

y

'



f

 

x

,

y

di

x



x

_n dan

y



y

 

x

_n 1 n

f

_ = nilai fungsi

y

'



f

 

x

,

y

di

x



x

_n_₁ dan

y



y

 

x

_n_₁  p n

f

= turunan ke-p fungsi

f

 

x

,

y

di

x



x

_n

dan

y



y

 

x

_n  p

1 n

f

_ = turunan ke-p fungsi

f

 

x

,

y

di

x



x

_n_₁

dan

y



y

 

x

_n_₁

n

y

= nilai fungsi y(x) di

x



x

_n 1



n

y

x



x

_n_₁

n = 0,1,2,3,…

Untuk p = 1 pada persamaan (22) menjadi :



0 1



0 1 1 1     n   n n b x a a x y



n



n n

b

x

a

x

y

₀





₀



₁ (23)



0 1



1 1 1   



n





n n

b

x

a

y

f



n



n n b x a y f ₀   ₁

Pengeliminasian koefisien

a

0

,

a

1

,

dan

b

0 pada (23)

menghasilkan: n n n n n n

y

f

y







   1 1 1 (24)

Untuk p = 3, persamaan (22) menjadi :





3 1 3 2 1 2 1 1 0 1 0 1       n   n  n  n n b x a a x a x a x y





3 3 2 2 1 0 0 n n n n n

b

x

a

x

a

x

a

x

y











1 2 1 3 1 2 1 1 0 1 

2



3

  



n





n



n



n n

b

x

a

x

a

x

y

f

(25)



n



n n n n

b

x

a

x

a

x

y

f

₀





₁



2

₂



3

₃ 2



 

_

_

1 1 3 2 1 0 1 1 

2

6



2

 



n





n



n n

b

x

a

x

f

 





n n n n

b

x

a

x

f

0

2

6

3

2

1









Pengeliminasian koefisien-koefisien

a

₀

,

a

₁

,

a

₂

,

a

₃ dan

0

b

menghasilkan Persamaan (26) di bawah.: 3.2. Pendekatan Rasional Berpenyebut Fungsi Kuadrat

Misalkan Fungsi Rasional dibentuk dalam bentuk sebagai berikut :

 

₂ n n 1 0 P 0 s s s

x

b

x

a

x

R







 ₍₂₇₎ dengan

0

2 1 0



b

x

n



x

n



b

0

a

hingga

a

_p serta

b

₀,b1adalah koefisien yang

belum diketahui nilai-nilainya R bernilai Riil



,

1





x

n

x

n

x

, n = 0,1,2,3,…,N

Persamaan (27) memiliki koefisien yang tidak diketahui sebanyak

(p + 4) koefisien (28)

Dengan menggunakan prinsip polinomial oskulasi pada (27)dalam interval



x

_n

,

x

_n_₁



diperoleh sistem persamaan berikut :





_

        p s s n s n n n b bx x a x y 0 1 2 1 1 1 0 1





_





p s s n s n n n

b

x

a

x

y

0 2 1 0

 





           

_

_

1 2 2 1 1 1 1 4 2 2 3 4 3 1 1 1 1 1 1 1 2 2 1 1 1

4

2

12

2

12

n n n n n n n n n n n n n n n n n n

y

h

f

h

f

h f f

h f

f

h f

f

h f

f

hf

h f

y

        















……….. (26)

(5)





1



1 1



1 1 1 2 1 1 1 0 1  2          



 n  n p s s n s n n n b bx x sa x y b x f





n



n



p s s n s n n n

b

x

sa

x

y

b

x

f

1

2

1 1 2 1 0











 









1



1 1



1 2 2 1 2 1 1 1 0 ) 1 ( 1

1

2



2



2

      









n



n



n p s s n s n n n

b

x

s

a

x

f

b

x

y

f









n



n



n p s s n s n n n

b

x

s

a

x

f

b

x

y

f

1

2

1

2

2 2 2 1 0 ) 1 (













 













1 1



1 ) 1 ( 1 3 3 1 2 1 1 1 0 ) 2 ( 1

1

2

3



2



6

      









n



n



n p s s n s n n n

b

x

s

a

x

f

b

x

f











n



n



n p s s n s n n n

b

x

s

a

x

f

b

x

f

1

2

3

(1) ₁

2

6

3 3 2 1 0 ) 2 (













  .













 2 1 1 1 ) 1 ( 1 2 1 1 1 0 ) ( 1

(

1 )

2

1

       









n





np p n n n p n

b

x

ap

p

f

b

x

p

f













 2 1 ) 1 ( 2 1 0 ) (

1

2 )

1 (

















p n n p n n n p n

b

x

ap

p

f

b

x

p

f

………. (29) dengan p = 1,2,3,… n

f

= nilai fungsi

y

'



f

 

x

,

y

_di n

x



dan

y



y

 

x

_n 1 n

f

_ = nilai fungsi

y

'



f

 

x

,

y

di

x



x

_n_₁ dan

y



y

 

x

_n_₁  p

n

f

= turunan ke-p fungsi

f

 

x

,

y

di

x



x

_n dan

y



y

 

x

_n  p

1 n

f

_ = turunan ke-p fungsi

f

 

x

,

y

di

x



x

_n_₁ dan

y



y

 

x

_n_₁

n

y

x



x

_n 1



n

y

x



x

_n_₁

n = 0,1,2,3,…

0

2 2 1 0



b

x



b

x



b

,

x



x

_n

,

x

_n_₁

Untuk p = 2 persamaan (29) menjadi :





2 1 2 1 1 0 2 1 1 1 0 1     



n



n





n



n n

b

x

a

x

a

x

y





2 2 1 0 2 1 0 n n n n n

b

x

a

x

a

x

y











1 2 1 1



1 1



2 1 1 1 0 1  

2

 

2

 



n



n





n



n



n n

b

x

a

x

y

b

x

f

(30)



n n



n n



n



n

b

x

a

x

y

b

x

f

₀



₁



2



₁



2

₂



₁



2 



2 1



1 1



1 2 1 1 1 0 ) 1 ( 1  

2



2



2

 



n



n





n



n



n n

b

x

a

f

b

x

y

f



n n



n



n



n n

b

x

a

f

b

x

y

f

(1) ₀



₁



2



2

₂



2

₁



2 

2

Pengeliminasian koefisien

a

₀

,

a

₁

,

a

₂,

b

₀ dan b1 menghasilkan:

 

_

_

_{ }

_

_

 

_{ }

       

_

_

2 1 1 1 3 1 2 1 1 3 1 1 1 4 2 1 1 4 2 1 3 1 2 3 2 1 1 4 1

4

2

12

2

4

2

         















n n n n n n n n n n n n n n n n n n n n

y

f

h

f

h

f

h

f

h

f

h

f

h

f

h

f

h

y

…….. (31)

Untuk p = 4 persamaan (29) menjadi :

(6)





4 4 3 3 2 2 1 0 2 1 0 n n n n n n n

b

x

a

x

a

x

a

x

a

x

y











1



1 1



3 1 4 2 1 3 1 2 1 2 1 1 1 0 1  

2



3



4

 

2

 



n



n





n



n



n



n



n n

b

x

a

x

a

x

a

x

y

b

x

f



n n



n n n n



n



n

b

x

a

x

a

x

a

x

y

b

x

f

₀



₁



2



₁



2

₂



3

₃ 2



4

₄ 3



₁



2 



1



1 1



1 2 1 4 1 3 2 2 1 1 1 0 ) 1 ( 1  

2

6



12



2



2



2

 



n



n





n



n



n



n



n n

b

x

a

x

a

x

f

b

x

y

f



n n



n n n



n



n n

b

x

a

x

a

x

f

b

x

y

f

(1) ₀



₁



2



2

₂



6

₃



12

₄ 2



2

₁



2 

2 



3 4 1 1



1 1



1 2 1 1 1 0 ) 2 ( 1  

6

24



3

1



2



6

 



n



n





n



n



n



n n

b

x

a

x

d

f

b

x

f



n n



n n



n



n n

b

x

a

x

d

f

b

x

f

6

3

24

4

3

1

2

6

2 1 0 ) 2 (













Pengeliminasian koefisien-koefisien

a a a a a

₀

, ,

₁ ₂

,

₃

,

₄,

b

₀ dan

b

₁ menghasilkan :

 

_{ }

_

_

 





 

_{ }

   

_{ }

               

_

_

 

    1 2 ₃ ₂ 1 2 7 3 3 1 1 2 3 1 2 3 3 4 1 1 1 2 1 2 1 1 4 5 5 1 1 1 1 1 1 1 2 1 5 6 4 1 1 1 1 2 2 1 2 1 2 4 7 7 1 1

3

72

12

36

12

72

3

2

n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n n

y

h

f

h

f

h

f

h

f

h

f

h f

f

h f

f

h f

f

h f

f

h f

f

h f

f

h f

f f

h f

f

h f

f

h f

f

               













       

_{ }

   

 





                  2 1 2 2 2 2 2 1 7 5 6 1 1 1 1 2 2 1 2 2 2 3 1 1 1 1 2 1 1 1 2 3 4 4 5 1 1 1 1 1 1 1 3 3 6 1

2

12

288

216

72

24

72

12

216

72

4

n n n n n n n n n n n n n n n n n n n n n n n n n n n n

f

h f

f

h f

f

h f

f

h

f

h f

f

h

f

h f

f

h f

f

h f

f

h f

f

h f

f

h f

f

h f

f

h f

             













_

_

_











         

_

_

_

_

 

_

_

 

_

_

 

_

_

 

_

_

_

_

2 2 4 2 1 2 1 5 1 1 1 1 1 2 2 3 1 1 1 1 2 1 2 2 3 1 1 1

24

12

432

144

12

144

12

288

n n n n n n n n n n n n n n n n n n n n n n n n n

f

h f

f

h f

f

hf

y

hf

y

h f

y

h f

y

h f

y

h f

y

           



















_



_

_

_

_







(32)

Contoh Numerik : Penggunaan Skema Aproksimasi Rasional

Diberikan suatu masalah nilai awal orde pertama dengan bentuk :

2

1 y

y







(33)

dengan syarat awal

 

0 

1 y

(34)

Solusi eksak dari persamaan diferensial (33) dengan syarat (34) adalah











 



4 

x

tg

y

(35)

Dengan menggunakan skema (24), (26), (31) dan (32) untuk h = 0.01 dalam interval [0,0.7], diperoleh hasil integrasi numerik sebagaimana diberikan dalam Table 2 hingga Tabel 5.

Tabel 1. Solusi eksak untuk

x



0

hingga

x



0 ,

7

dengan

h



0 ,

1 x





4 





tg

x

y

0 1.000000000 0.1 1.223048881 0.2 1.508497647 0.3 1.895765123 0.4 2.464962757 0.5 3.408223443 0.6 5.331855244 0.7 11.68137380

(7)

Tabel 2. Nilai aproksimasi dan galat fungsi solusi MNA (33) dengan syarat(34) menggunakan skema (24) untuk h = 0.01 n

x

_n

y

_n Rasional

 

y

_R₁

y

_n eksak

 

y

_nE

y

_R₁



y

_nE 0 0.000000000 1.0000000000 1.000000000 0.0000000000 1 0.100000000 1.2230530404 1.223048881 0.0000041594 2 0.200000000 1.5085085662 1.508497647 0.0000009192 3 0.300000000 1.8957880934 1.895765123 0.0000229704 4 0.400000000 2.4650099324 2.464962757 0.0000471754 5 0.500000000 3.4083285818 3.408223443 0.0001051388 6 0.600000000 5.3321495352 5.331855244 0.0002942912 7 0.700000000 11.6829777080 11.68137380 0.0016039080

Tabel 3. Nilai aproksimasi dan galat fungsi solusi MNA (33) dengan syarat (34) menggunakan skema (26) untuk h = 0.01 n

x

_n

y

_n Rasional

 

y

_R₁

y

_n eksak

 

y

_nE

y

R1



y

nE 0 0.000000000 1.0000000000 1.000000000 0.0000000000 1 0.100000000 1.2230488454 1.223048881 0.0000000346 2 0.200000000 1.5084975746 1.508497647 0,0000000724 3 0.300000000 1.8957650021 1.895765123 0.0000001209 4 0.400000000 2.4649625480 2.464962757 0.0000002090 5 0.500000000 3.4082230535 3.408223443 0.0000003895 6 0.600000000 5.3318543020 5.331855244 0.0000009420 7 0.700000000 11.6813694820 11.68137380 0.0000043180

Tabel 4. Nilai aproksimasi dan galat fungsi solusi MNA (33) dengan syarat (34) menggunakan skema (31) untuk h = 0.01 N n

x

y

_n Rasional

 

y

_R₁

y

_n eksak

 

y

_nE

y

_R₁



y

_nE 0 0.000000000 1.0000000000 1.000000000 0.0000000000 1 0.100000000 1.2230487743 1.223048881 0.0000001057 2 0.200000000 1.5084973956 1.508497647 0.0000002514 3 0.300000000 1.8957646513 1.895765123 0.0000004717 4 0.400000000 2.4649618134 2.464962757 0.0000009436 5 0.500000000 3.4082214783 3.408223443 0.0000019647 6 0.600000000 5.3318501259 5.331855244 0.0000051181 7 0.700000000 11.6813481170 11.68137380 0.0000256830

Tabel 5. Nilai aproksimasi dan galat fungsi solusi MNA (33) dengan syarat (34) menggunakan skema (32) untuk h = 0.01 n n

x

y

_n Rasional

 

y

_R₁

y

_n eksak

 

y

_nE

y

_R₁



y

_nE 0 0.000000000 1.0000000000 1.000000000 0.0000000000 1 0.100000000 1.2227673264 1.223048881 0.0002815546 2 0.200000000 1.5076272351 1.508497647 0.0008704119 3 0.300000000 1.8936294529 1.895765123 0.0021356701 4 0.400000000 2.4598124210 2.464962757 0.0051503360 5 0.500000000 3.3944252449 3.408223443 0.0137981981 6 0.600000000 5.2829904289 5.331855244 0.0488648151 7 0.700000000 11.302789129 11.68137380 0.3785846710

(8)

4. KESIMPULAN

Dari uraian pembahasan dapat diambil kesimpulan berikut. Sejumlah skema pendekatan rasional bentuk implisit telah diperoleh dengan menggunakan metode eliminasi koefesien yang tidak diketahui nilainya pada pendekatan rasional dengan penyebut fungsi linier dan pendekatan rasional dengan penyebut fungsi kuadrat. Selanjutnya, dalam contoh kasus Masalah Nilai Awal yang diberikan, diperoleh bahwa pendekatan menggunakan skema (24),(26) dan (31) memberikan hasil yang lebih akurat dibandingkan dengan skema (32), hal ini dapat dilihat dari galat yang diperoleh dari masing-masing skema aproksimasi tersebut.

DAFTAR PUSTAKA

1. Lapidus L., & Seinfeld, J.H. 1971. Numerical Solution of Ordinary Differential Equations. Academic Press, New York.

2. Lambert, J.D. & Shawn, B. 1964. On The Numerical Solution of

y

'



f

 

x

,

y

By A class Formulae Based of Rasional Approximation. J. Comp. 98-105.

3. Feng, K. and Shang, Z.-J. 1995 Volume-preserving algorithms for source-free dynamical systems. Numer. Math. 71: 451-463

4. Quispel, G. R W. and Dyt, C. 1998 Volume-preserving integrators have linear error growth. Physics Letters A. 242; pp 25-30.

5. Suharsono S. 2005. Integrasi Sistem Kepler dengan Dua First Integral. Jurnal Matematika Murni dan Terapan, 3 (1) 8-12.

6. Zakaria L. dan Gina R. 2000. Penyelesaian secara

Numerik Masalah Nilai

Awal

y





f



x

,

y

,

y





Berdasarkan Pendekatan Rasional. J. Sains Tek., 3 ( 5) 75-85. 7. Zakaria, L. 2005. Studi Interpolasi Polinom Dalam

Pembaruan Tabel Data Berjarak Sama (Studi Kasus : Interpolasi Pada Nilai Fungsi Rasional), Jurnal Matematika Murni dan Terapan, Vol: 1 ( 2): 33-40.