A Research about Frequent Contextual Termset
Tubagus M. Akhriza
School of Communication and Information System Shanghai Jiao Tong University
Shanghai, P.R. China akhriza@sjtu.edu.cn
Yinghua MA, Jianhua LI
School of Information Security Engineering Shanghai Jiao Tong University
Shanghai, P.R. China
Abstract – One of problems in frequent pattern (FP) mining is how to reduce the number of pattern in collection which usually in huge numbers. To solve the problem, two classes of approximate frequent pattern i.e. closed frequent pattern and maximal frequent pattern have been proposed. In fact, the number of closed frequent pattern is still very huge and leads to ineffectiveness and inefficiency when exploring the pattern. In contrast, the number of maximal frequent termset (MFT) in collection is usually smaller than CFT. MFT is able to represent the long or specific termset in dataset. Unfortunately, it doesn’t represent the support of its subset. Meanwhile, our previous work has introduced a novel notion about frequent contextual termset (FCT). The number of FCT’s pattern in collection is much smaller than CFT’s and this is an advantage of using FCT. However, the further study about FCT has not been reported yet. In this paper we present our further investigation about FCT compared to CFT and MFT. The investigation is aimed to figure out the position of FCT amongst those two classes of frequent termset. Experimental work and mathematical approach are developed for this investigation. One of the results shows that FCT is able to represent both CFT and MFT.
Keywords–Frequent Contextual Termset, Approximate Frequent Pattern, Document Intersection
I. INTRODUCTION
The approximate frequent patterns (AFP) of dataset are the patterns which are not presenting the entire frequent pattern but acceptable representing the fact of the given dataset. AFP is proposed to solve FP problem particularly in reducing the number of pattern in collection which usually in huge number [1, 2]. It is happened when very small interestingness threshold called minimum support (minsupp) is applied to mine the frequent pattern, since the sub-patterns of frequent patterns are also frequent. Two approaches have been proposed to solve such problem i.e. closed frequent pattern and maximal frequent pattern.
Experimental fact shows that the number of closed frequent pattern is also still very huge, particularly in mining the dataset containing linguistic context such as news, paper abstracts or search engine results. The number of closed frequent termset (CFT) pattern in collection can reach hundred thousands to millions pattern and leads to ineffectiveness and inefficiency when exploring the patterns. It happened because such dataset is unstructured and the number of term is unpredictable. In contrast, the number of maximal frequent termset (MFT) generated from the same dataset is smaller than CFT. Maximal frequent termset is
also able to represent the specificity amongst documents of dataset; but many papers explain the weakness point of maximal pattern is that it doesn’t represent the support of its subset.
Meanwhile, the notion about Frequent Contextual Termset (FCT) has been introduced firstly in our previous work [3]. The FCT is produced by a concept called document interestingness, which works based on document intersection. The document intersection works similar with transaction intersection which has been implemented to mine closed frequent itemset [4, 5, 6]. The main different point between our approach with the traditional one is that we only enumerate the pair of document in combination C(N,2) (N=number of document) while the traditional enumerates 2N document combination. Mathematically, our approach is faster than the traditional methods and the number of pattern is also much smaller than CFT. Moreover, the exact maximal number of FCT is clearly predictable i.e. C(N,2)=N(N-1)/2, while the traditional approaches is unpredictable since it depends on the terms composition inside.
Such facts show some benefit of using FCT particularly in providing a very compacted or compressed AFP. However, there are some questions arises for FCT, particularly in order to declare that FCT is acceptable as good AFP: first, is FCT able to represent at least one of the CFT or MFT? Second, because of the small number of pattern, does FCT loss much information? And third, since in FCT algorithm there is no computation of support thus, how to provide the approximation support of termset? To answer the first question, firstly from dataset samples we generate the collection of CFT using well-known algorithms i.e. ChARM, and Carpenter; and MFT using MAFIA, while FCT is generated using our proposed algorithm: FACTA. Next step is to formulate and testify some set relations amongst collections. More detail of the relation is explained in section 4, experimental framework. To answer second question, we investigate the terms composition between such collections. Intuitively, if there is no significantly different in term composition, then we can conclude that there is not much loss of information in FCT. And for the third question: In this paper we propose a novel approach to approximate the support by calculating the document identifier (docid) which is saved in the same time with mining FCT. Such approach is named as On-demand Approximate Support Calculation.
II. CLOSED AND MAXIMAL FREQUENT ITEMSET
There are two approaches can be used to mine the closed frequent itemset (CFI) [6]: the first is item’s based
enumeration method which is implemented in most known approaches such as ChARM [7]. Basically, the items’ enumeration approach enumerates 2|I| term’s combination to generate the termset, where |I|=number of item. In item’s enumeration based mining, CFI is defined as any frequent itemset x in collection which frequent and has no proper superset having the same support with x. Besides the item’s enumeration based mining, an alternative algorithmic scheme to mine the closed frequent itemset is by intersecting the transaction [4, 5, 6]. Such approach enumerates 2|D| transaction combination to mine the termset, where |D|=number of document. The items’ enumeration methods are effective when |I|<|D|, and vice versa the transaction enumeration is effective when |D|<|I|. In transaction intersection approach, Meilikainen [6] defines the closed set as follows:
According to [4], there are (still) three approaches have been proposed to utilize transaction intersection to mine CFI. An algorithm called CARPENTER is proposed in [5], the cumulative scheme [6] and the improvement of cumulative scheme in [4] proposed by Borgalt et al.
Maximal frequent itemset (MFI) is any frequent itemset x in collection which has no proper superset. Through this definition, we understand that MFI doesn’t represent support of its subset. But it is important to represent long or specific itemset inside of dataset. The study about mining MFI is firstly done by Bayardo [8]. Burdick et al. in [9] propose an efficient algorithm for mining MFI called MAFIA.
III. THE FREQUENT CONTEXTUAL TERMSET
A. Formalization of FCT
This section provides some definitions of FCT which some of them have been introduced in [3]. Supposed D is a document set and Di (i=1,.., n) are the documents of D. Ti is
the terms set of Di ∈ D. For each pair Di, Dj ∈D, production
function P is defined as Equation (1)
Definition 2. A Termset Production Function P of pair of
documents (Di, Dj) which produces termset T is defined as equation (1) × is binary operator which is defined as interestingness of a pair of document Di and Dj as definition 2. The product of P is T ∈ (Di ∩ Dj) i.e. the termset which is named as the Contextual Termset (CT). T is the longest termset taken from pair of documents which produce it, thus the equation (1) can be re-written as equation (2)
(
)
Definition 3. (Document Interestingness) A pair of
document Di, Dj ∈ D is interesting if satisfies specificity coefficient α such as equation (3)
0 Dj. In the other word, two documents are interesting if they posses common terms which satisfy α. To record the number of document producing the CT, we propose the Production Support PSupp as following definition.
Definition 4. A Set of Documents which produce
contextual termset T is denoted as DP(T)={< i, j>| T ∈ (Di∩Dj), i, j=1,..,n} or simplified as DP(T) = { i, j, …, n }
For example: DP(T) = {<0,1>, <0,4>} means that T is produced by docid’s pair (0,1) and (0,4) or exists in document with docid 0, 1 and 4; or simply written as DP(T) = {0, 1, 4}. Definition 4 is useful to give more information about the termset, i.e. the documents containing the termset.
Definition 5. The Production Support (PSupp) of
contextual termset is determined by the number of document produce the termset using definition 4. Supposed DP is a set of Documents which produce termset T then Psupp is defined as equation (4)
Psupp(T) = |DP(T)| (4)
Definition 6. (Frequent Contextual Termset) Frequent
Contextual Termset (FCT) is contextual termset which PSupp satisfies given minimum support MinPsupp.
Psupp(CT) ≥ MinPsupp (5)
In this section, the term minsupp is also used to denote minimum support threshold which is defined in association rule based mining [8]. The Cov(T) is a notation for the Cover of T i.e. the set of documents containing termset T.
Definition 7. The support of a Contextual Termset T is the number of documents containing T.
Supp(T)=|Cov(T)| (6)
Property 1. |DP(T)| ≤|Cov(T)|, T∈ F.
Proof: Cov(T) is calculated from enumeration in 2N combination, while DP(T) is in C(N,2). Since C(N,2) ≤ 2N
then it is possible that member of Cov(T) doesn’t exist in DP(T); thus |DP(T)|≤|Cov(T)|.
B. FACTA: an Algorithm for Mining FCT
In this paper, we introduce FACTA as an algorithm for mining FCT which has improved the previous one proposed in [3]. Hashtable is implemented to provide fast, dynamic computation and storage of found termset T. Notation <i, j> on line 5f expresses the pair of docids producing T. On line 5e, notation <i, j>++ means string concatenation i.e. to add current <i, j> to previous existing <i, j>.
Algorithm 1. FACTA : FCT mining Algorithm
Prepare FCTDict Å a hashtable for FCT
Input: DocÅDocuments of Dataset D, alphaÅminimum specificity coefficient
Output: FCTDict
1. For i= 0 to D.size‐1 2. For j = I + 1 to D.size
a) T = Doc(i)∩Doc(j) b) If |T|>= alpha Then
c) If FCTDIct.contains(T) then d) FCTDictc.Key(T)= <I,j>++ e) Else
f) FCTDict.add(T,<I,j>)
g) End if
h) Endif
3. Next
4. Next
IV. EXPERIMENTAL WORK
A. Dataset Samples
25 dataset samples are generated from some datasets i.e. Web-KB (shorted as Web), 20 News Group (20NG) and Mushroom. Each sample contains 100 documents and from those samples, the FCT, CFT and MFT are mined. 20NG provides 20 classes and from each class we generate one sample. Thus from 20NG we have 20 sample. From Web which has 4 classes, we generate 4 samples. Particularly from mushroom, we only generate 1 sample. Thus, we have total 25 samples. Web and 20NG are dataset containing linguistic context. Mushroom is not containing linguistic context but we would like to inspect the FP produced from it. B. Experimental Framework
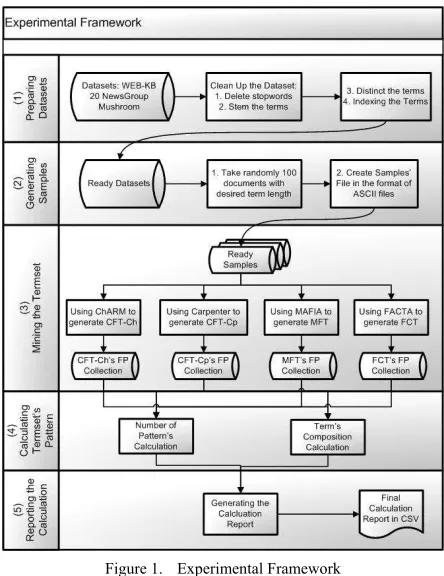
Fig. 1 shows the experimental framework used in our work. The overall experiment framework is explained as follows:
(1) Preparing the datasets – Following steps are applied
to each datasets: (a) Deleting stop-words (b) Stemming the terms into their root-form, except terms in mushroom is no need to stem. (c) Distinct the terms, except the mushroom (d) Indexing the terms. Above steps produce ready datasets.
(2) Generating the samples – For each dataset, following
steps are applied to generate the 25 samples: (a) Take randomly 100 documents with desired term length (b) For each classes, create ASCII text file in following format: <listid> <docid> <terms‐number> <the terms
in indexed form>. ChARM and MAFIA use such format, while in FACTA and CARPENTER we simply put <the terms in indexed form> on each line.
(3) Mining the termset – We use ChARM and
CARPENTER to mine CFT-Ch and CFT-Cp respectively; and MAFIA to mine MFT. The minsupp is set to 0.02 or 2/100, since FACTA automatically produces the FCT with minsupp 2. It is because all termset are produced by pairs of documents. The specificity coefficient α is set to 1.
(4) Calculating the Termset’s Pattern– This process
contains some steps: (a) Each termset in output files of CFT-Ch, CFT-Cp, MFT and FCT are loaded into a sorted set. Each term in termset is split and sorted ascending to make them accurate for the following set’s operation process (b) Number of pattern analysis: In this step we utilize some set’s operation to have following relation: (FCT∩CFT-Ch), (FCT∩CFT-Cp), (FCT∩MFT). (MFT⊂CFT) to get the status whether the MFT is proper set of FCT, analogically for (FCT⊂CFT-Cp) and (FCT⊂CFT-Ch). (c) Terms composition analysis: for this analysis, from each sample we collect all existing terms; collect them into a sorted set to guarantee that there is no redundant term is saved. Above set relations are used to inspect the terms composition in each collection.
Figure 1. Experimental Framework
(5) Reporting the Calculation– a process to generate the
report of termset analyzing process.
V. EXPERIMENTAL RESULT AND ANALYSIS
A. Experimental Results
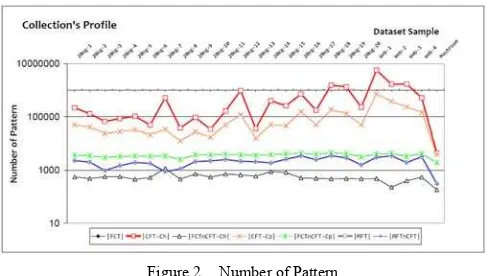
Fig. 2 shows the graph of number of pattern in 25 samples. Obviously, the number of FCT’s pattern is much less than CFT-Ch (the highest line) and CFT-Cp (below the CFT-Ch), while MFT’s line is relatively close to FCT. Some extreme results are shown by CFT-Ch with millions patterns. Such in Web1, CFT-Ch contains more than 5 millions pattern and CFT-Cp about 700 thousands, while in FCT is only 4084 which not more than C(N,2) = 100*99/2 = 4950 patterns. The MFT contains 3073 pattern.
Figure 2. Number of Pattern
As the summary, the relation of number of pattern in collection is |MFT| < |FCT| < |CFT-Cp| < |CFT-Ch| and the relation between the collection is MFT ⊆ FCT ⊆ CFT-Cp; MFT ⊄ CFT-Ch; FCT ⊄ CFT-Ch. It is shown that FCT is closed frequent termset and contains MFT.
Figure 3. Terms Composition
Fig. 3 shows the graph of terms composition. All of line is very tight, which shows that there is no different between the terms in all patterns. A surprising result is discovered here. Although the number of FCT’s pattern is much smaller than CFT’s, but the term composition is not different. It shows that CFT saves too much repeating terms which is not necessary in exploring pattern from dataset with linguistic context, since the short termset can be absorbed by the longer without loss any information about the termset; and the common people still could understand the meaning of the termset. Such pattern is named as common understandable context pattern. The red line on 20Ng-3 sample shows that some termsets in FCT and CFT-Cp do not exist in CFT-Ch. B. Mathematical Analysis
Some mathematical proofs have been derived, but here we explain three important ones: firstly, the proof that FCT is proper subset of CFT is clear because the approach of document interestingness (DI) is basically the same with transaction intersection (definition 1), and because DI takes the longest pattern amongst documents thus FCT is also the proper superset of MFT (Equation 2). Secondly, any member of FCT is guaranteed supported by very small minsupp i.e. 2/N (Definition 2–3) which in current approaches it is too small to be implemented because will generate a huge number of patterns, whereas for discovering more surprising
knowledge, there shouldn’t be any limitation of “interestingness” threshold. At this point of view, FCT also shows the benefit. Thirdly is an approach for approximating the support of termset in following definition:
Definition 9. The approximation of support of termset T
can be calculated by using on-demand calculation function f(T) as following equation:
{ }
U
i n DPi T Tf
..
1 ( *) )
(
∈
= (7)
With i is the number of DP i.e. set of document which producing T* = T and T’s supersets. By this function, if we can get the approximation support of termset T by calculating some pairs of docids of termsets containing T (see definition 4 and property 1).
VI. CONCLUSION AND FUTURE WORK
Several advantages of using FCT have been described. Both results in number of pattern and terms composition show that FCT is acceptable to summarize or approximate the contextual facts in dataset. FCT can be mined directly from dataset using FACTA which is also able to provide useful information about the docids producing the termset. Moreover, FCT also opens the way to discover more surprising knowledge without limitation of interestingness threshold. A notion about inspecting the terms composition to compress the pattern is indirectly proposed in this paper as well. For the future work, we plan to develop a framework for frequent pattern mine-engine based on FCT.
ACKNOWLEDGMENT
REFERENCES
[1] J. Han · H. Cheng · D. Xin · XF. Yan. 2007. Frequent pattern mining: current status and future directions. Data Min Knowl Disc (2007) 15:55–86. Springer. DOI 10.1007/s10618-006-0059-1.
[2] M. Hasan. 2009. Summarization in Pattern Mining. Citeseerx. doi=10.1.1.153.7803
[3] Tb. M. Akhriza, Y. MA and J. LI. 2011. Text Clustering using Frequent Contextual Termset. Accepted for publication in IEEE 2011 ICIII. 26th-27th November 2011. Shenzhen. China.
[4] C. Borgelt, X. Yang, R.N. Cadenas, P.C. Saez and A.P. Montano. 2011. Finding Closed Frequent Item Sets by Intersecting Transactions. EDBT 2011, March 22–24, 2011, Uppsala, Sweden. ACM
[5] T. Mielikäinen. 2003. Intersecting Data to Closed Sets with Constraints. Citeseerx. doi=10.1.1.2.1644
[6] F. Pan, G. Cong, J. Yang, M.J. Zaki. Anthony K and H. Tung. 2003. CARPENTER: Finding Closed Patterns in Long Biological Datasets. SIGKDD ’03, August 2427, 2003, Washington, DC, USA.
[7] M.J. Zaki and Hsiao. 1999. CHARM: An Efficient Algorithm for Closed Association Rule Mining
[8] Bayardo R.J. 1998. Efficiently mining long patterns from databases. In: Proceeding of the 1998 ACM-SIGMOD, Seattle,WA, pp 85–93 [9] Burdick D, Calimlim M, Gehrke J. 2001. MAFIA: a maximal
frequent itemset algorithm for transactional databases. In: Proceeding of the 2001 ICDE’01, Heidelberg, Germany, pp 443–452