PENYELESAIAN PERSAMAAN GELOMBANG ELASTIS MENGGUNAKAN METODE BEDA HINGGA GRID SELANG- SELING: ASPEK MATEMATIKA DAN ASPEK PENDIDIKANNYA

(1)

i TESIS

PENYELESAIAN PERSAMAAN GELOMBANG ELASTIS

MENGGUNAKAN METODE BEDA HINGGA GRID

SELANG-SELING: ASPEK MATEMATIKA DAN ASPEK

PENDIDIKANNYA

MARIA YULIANI DANGGO 161442014

PROGRAM STUDI PENDIDIKAN MATEMATIKA PROGRAM MAGISTER JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS SANATA DHARMA

YOGYAKARTA 2018

(2)

ii

THESIS

SOLUTION TO THE ELASTIC WAVE EQUATION USING A

STAGGERED GRID FINITE DIFFERENCE METHOD:

MATHEMATICAL ASPECTS AND ITS EDUCATIONAL

ASPECTS

MASTER OF MATHEMATICS EDUCATION PROGRAM MATHEMATICS AND SCIENCE EDUCATION DEPARTMENT

FACULTY OF TEACHER TRAINING AND EDUCATION SANATA DHARMA UNIVERSITY

(3)

iii TESIS

PENYELESAIAN PERSAMAAN GELOMBANG ELASTIS

MENGGUNAKAN METODE BEDA HINGGA GRID

SELANG-SELING: ASPEK MATEMATIKA DAN ASPEK

PENDIDIKANNYA

Diajukan untuk memenuhi salah satu syarat memperoleh derajat Magister Pendidikan pada Program Magister Pendidikan Matematika

PROGRAM STUDI PENDIDIKAN MATEMATIKA PROGRAM MAGISTER JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS SANATA DHARMA

(4)

(5)

(6)

vi

HALAMAN MOTTO

I see and I forget. I hear and I remember.

I do and I understand.

- Confucius –

(7)

vii

HALAMAN PERSEMBAHAN

Tesis ini saya persembahkan untuk

Bapa Iu, Mama In, kakak Nobing, Uchan, Yoan, Yayan dan Deden yang selalu mendoakan dan mendukung saya.

(8)

viii

PERNYATAAN

Dengan ini saya menyatakan bahwa Tesis ini tidak terdapat karya yang pernah diajukan untuk memperoleh gelar akademik di suatu Perguruan Tinggi, dan sepanjang pengetahuan saya juga tidak terdapat karya atau pendapat yang pernah ditulis atau diterbitkan oleh orang lain, kecuali yang secara tertulis diacu dalam naskah ini dan disebutkan dalam daftar pustaka.

Yogyakarta, 30 Juli 2018

(9)

ix

ABSTRAK

Maria Yuliani Danggo, 2018. Penyelesaian Persamaan Gelombang Elastis Menggunakan Metode Beda Hingga Grid Selang-Seling: Aspek Matematika dan Aspek Pendidikannya. Tesis. Program Studi Magister Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.

Beberapa masalah dalam kehidupan sehari-hari dapat dimodelkan secara matematis. Pemodelan masalah ini bertujuan untuk mempermudah menentukan solusi dari masalah tersebut menggunakan ilmu matematika. Salah satu model matematika dari masalah nyata adalah persamaan gelombang elastis. Dalam menentukan solusi dari persamaan gelombang elastis ini, diperlukan suatu metode yang sesuai dengan masalah gelombang elastis.

Pada penelitian ini, metode yang digunakan untuk menyelesaikan persamaan gelombang elastis adalah metode beda hingga grid selang-seling. Metode ini berhasil menyelesaikan persamaan gelombang elastis dengan nilai awal yang halus (smooth). Solusi yang diperoleh berupa pendekatan analitis yang dihitung menggunakan aplikasi program MATLAB.

Pada penelitian ini juga dikaji tentang kemampuan komunikasi matematik yang dilaksanakan di Sekolah Dasar Negeri 2 Kragilan Gantiwarno. Materi matematika yang dipelajari dalam proses pembelajaran tersebut adalah operasi penjumlahan dan pengurangan. Konsep yang digunakan untuk menyajikan soal-soal dalam penelitian ini adalah konsep gelombang elastis. Hasil penelitian ini menunjukkan bahwa dari 18 siswa kelas VI SD Negeri 2 Kragilan Gantiwarno tahun 2017, terdapat: (1) 9 siswa sudah mampu memenuhi 2 indikator NCTM, yaitu indikator kemampuan dalam menggunakan istilah-istilah, notasi-notasi matematika untuk menyajikan ide dan indikator kemampuan mendemonstrasikan serta menggambarkan melalui lisan dan tulisan mengenai konsep operasi penjumlahan dan pengurangan; (2) 9 siswa sudah memenuhi ketiga indikator NCTM, yaitu indikator kemampuan dalam menggunakan istilah-istilah, notasi-notasi matematika untuk menyajikan ide, indikator kemampuan memahami menginterpretasikan secara lisan, tulisan maupun dalam bentuk visual lainnya, dan indikator kemampuan mendemonstrasikan serta menggambarkan melalui lisan dan tulisan mengenai materi operasi penjumlahan dan pengurangan, meskipun terdapat sedikit kekurangan dalam penulisan informasi dalam menyelesaikan soal.

Kata-kata kunci : metode beda hingga grid selang-seling, gelombang elastis, kemampuan komunikasi matematik.

(10)

x

ABSTRACT

Maria Yuliani Danggo, 2018. Solution To The Elastic Wave Equation Using A Staggered Grid F inite Difference Method: Mathematical Aspects And Its Educational Aspects. Thesis. Master of Mathematics Education Study Program, Mathematics and Science Education Department, F aculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.

Some problems in everyday life can be mathematically modeled. Modeling this problem aims to make it easier to determine the solution of the problem using mathematical science. One mathematical model of the real problem is the elastic wave equation. In determining the solution of this elastic wave equation, we need a method according to the problem of elastic wave.

In this study, the method used to solve the elastic wave equation is a staggered grid finite difference method. This method successfully solves the elastic wave equation with a smooth initial value. The solution obtained is an analytical approach calculated using the MATLAB program application.

In this study also studied about the ability of mathematical communica tion which is implemented in SD Negeri 2 Kragilan Gantiwarno. Mathematical material learned in the learning process is the addition and subtraction operations. The concept used to present the problems in this research is the concept of elastic wave. The results of this study indicate that from 18 students of the 6th grade of SD Negeri 2 Kragilan Gantiwarno in 2017, there are: (1) 9 students have been able to meet 2 indicators of NCTM, namely indicators of ability in using terms, mathematical notations to present ideas and indicators of the ability to demonstrate and describe through oral and written about the concept of addition and subtraction operations ; (2) 9 students have met all three indicators of NCTM, ie indicators of ability to use terms, mathematical notations for presenting ideas, indicators of the ability to understand orally, in writing or in other visual forms, and indicators of the ability to demonstrate and illustrate through oral and written material addition and subtraction operations, although there are little shortcomings in the writing of information in solving the problem.

Keywords : A Staggered Grid Finite Difference Method, elastic wave equation, mathematical communication skills.

(11)

xi

LEMBAR PERSETUJUAN

PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma: Nama : Maria Yuliani Danggo

Nomor Mahasiswa : 161442014

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma suatu karya ilmiah yang berjudul :

PENYELESAIAN PERSAMAAN GELOMBANG ELASTIS

MENGGUNAKAN METODE BEDA HINGGA GRID SELANG-SELING: ASPEK MATEMATIKA DAN ASPEK PENDIDIKANNYA

beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma baik untuk menyimpan, mengalihkan dalam bentuk media lain, mengolahnya dalam bentuk pangkalan data, mendistribusikan secara terbatas dan mempublikasikan di Internet atau media lain untuk keperluan akademis tanpa meminta ijin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini yang saya buat dengan sebenarnya.

Dibuat di Yogyakarta Pada tanggal 30 Juli 2018

Yang menyatakan

(12)

xii

DAFTAR PUBLIKASI HASIL PENELITIAN TESIS

Sebagian hasil dari tesis ini telah dipresentasikan dalam konferensi internasional dan/atau dipublikasikan dalam jurnal internasional sebagai berikut: Maria Yuliani Danggo dan Sudi Mungkasi, “A Staggered Grid Finite Difference

Method for Solving Elastic Wave Equations”, Journal of Physics: Conference Series, Volume 909, Nomor 1, Artikel 012047, Tahun 2017 (terindeks Scopus), Link Artikel: http://doi.org/10.1088/1742-6596/909/1/0120457

(13)

xiii

KATA PENGANTAR

Pujian syukur dan terima kasih kepada Tuhan yang Maha Kuasa atas segala berkat dan bimbingan-Nya, sehingga tesis dengan judul “Metode Beda Hingga Grid Selang-seling untuk Menyelesaikan Persamaan Gelombang Elastis: Aspek Matematika dan Aspek Pendidikannya” ini dapat diselesaikan. Tesis ini disusun untuk memenuhi salah satu syarat memperoleh gelar Magister Pendidikan pada Program Magister Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pengetahuan, Universitas Sanata Dharma Yogyakarta.

Proses penyusunan tesis ini tidak terlepas dari bantuan dan dukungan dari berbagai pihak. Oleh karena itu, pada kesempatan ini penulis mengucapkan terima kasih yang tak terhingga kepada semua pihak yang terlibat dalam penyusunan tesis ini, terlebih khusus kepada:

1. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku dosen pembimbing yang telah meluangkan waktu dan penuh kesabaran untuk memberikan bimbingan dan arahan selama penyusunan tesis ini.

2. Bapak Dr. Marcellinus Andy Rudhito, S.Pd., selaku Ketua Program Studi Magister Pendidikan Matematika yang telah memberikan dukungan bagi penulis.

3. Bapak Dr. Yohanes Harsoyo,S.Pd.,M.Si., selaku dekan FKIP Universitas Sanata Dharma yang telah mengesahkan penulisan tesis ini.

4. Segenap dosen Program Studi Magister Pendidikan Matematika yang telah membantu dan memberikan dukungan kepada penulis selama menempuh kuliah, sehingga penulis dapat menyelesaikan studi dengan baik.

5. Segenap staf JPMIPA yang telah membantu dalam hal administrasi kampus selama penulis menjalankan studi di Universitas Sanata Dharma ini.

6. Orang tua penulis (Bapa Iu dan Mama In), kakak Nobing, Uchan, Yoan, Yayan dan Deden atas doa, dukungan dan hiburannya. Kalian adalah anugerah yang paling indah dari Tuhan dalam hidupku.

(14)

xiv

7. Yuan untuk semua dukungan, doa dan motivasinya; Melani dan Naomi untuk semua dukungan dan doanya, semoga kita bisa bertemu lagi ya Nam, Me; Cacek, Opy dan Deik untuk hiburannya ketika sedang jenuh; Mirbung, Tasya, Mega dan Anlaw yang selalu merindu dan menunggu untuk berkumpul bersama lagi, sebentar lagi kita bertemu, kawan!

8. Teman-teman seperjuanganku terkasih, Lintang, Apri dan Kak Ira, untuk semua bantuan dan masukannya. Terima kasih untuk semuanya dan semoga Tuhan selalu menyertai kalian.

9. Semua pihak yang tidak dapat disebutkan satu persatu, yang telah membantu proses penyusunan tesis ini.

Semoga tesis ini bermanfaat bagi pembaca.

Penulis,

(15)

xv DAFTAR ISI

HALAMAN JUDUL... i

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

HALAMAN MOTTO ...v

HALAMAN PERSEMBAHAN ...vi

PERNYATAAN KEASLIAN KARYA ...vii

ABSTRAK ... viii

ABSTRACT ... ix

PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... x

DAFTAR PUBLIKASI HASIL PENELITIAN TESIS ... xi

KATA PENGANTAR ... xii

DAFTAR ISI ...xiv

BAB I PENDAHULUAN ... 1

A. Latar Belakang MasalaH ... 1

B. Rumusan Masalah ...………...3 C. Tujuan Penelitian ...3 D. Manfaat Penelitian ...4 E. Prasyarat Materi ... 5 F. Tinjauan Pustaka ...6 G. Keterbaruan Penelitian ...6 H. Batasan Masalah………...6 I. Metode Penelitian …... 7 J. Sistematika Penulisan ... 7

BAB II : LANDASAN TEORI ...9

A. Persamaan Diferensial...9

B. Penurunan Persamaan Gelombang... 10

C. Penurunan Numeris ... 14

1. Turunan Beda Maju………..… 14

(16)

xvi

3. Turunan Beda Pusat ……….… 16

D. Persamaan Gelombang Elastis... 17

E. Metode Beda Hingga Grid Selang-seling... 19

BAB III HASIL PENELITIAN ………...22

A. Model Matematika Persamaan Gelombang Elastis...22

B. Metode Numerik Grid Selang-seling...23

C. Hasil Numerik ... 24

BAB IV ASPEK PENDIDIKAN…….………...28

A. Teori Perkembangan Piaget ... 29

1. Tahap Sensoris Motorik ………... 29

2. Tahap Pra-operasional ………. 29

3. Tahap Operasional Konkret ………. 30

4. Tahap Operasional Formal ………...……….30

B. Komunikasi Matematik ... 30

C. Hasil Penelitian dan Analisis ………...31

BAB V KESIMPULAN DAN SARAN ...47

A. Kesimpulan ...47

B. Saran ...48

DAFTAR PUSTAKA ...49

(17)

xvii

DAFTAR GAMBAR

Gambar 3.1 tekanan saat ... 25

Gambar 3.2 Tekanan ... 26

Gambar 3.3 Tekanan ... 26

Gambar 4.1.1 Hasil pekerjaan siswa untuk soal 1 ... 33

Gambar 4.1.6 hasil pekerjaan siswa untuk soal 2 ... 35

(18)

1 BAB I PENDAHULUAN

A. Latar Belakang

Dalam kehidupan sehari-hari terdapat berbagai masalah yang berkaitan dengan matematika. Masalah-masalah tersebut dimodelkan secara matematika agar lebih mudah diselesaikan. Model matematika dapat berupa suatu persamaan matematika atau sistem persamaan matematika. Dalam memodelkan masalah, kita harus menentukan faktor-faktor dominan yang mempengaruhi masalah tersebut. Setelah itu, dari faktor-faktor yang dikoleksi, dipilih faktor-faktor yang paling dominan dan kemudian dikaitkan dengan ilmu pengetahuan yang ada, seperti fisika, biologi, kimia, dan sebagainya.

Model masalah tersebut kemudian ditentukan solusinya dan dianalisis. Jika solusi yang diperoleh cukup sesuai dengan realita, maka solusi tersebut cukup realistis dan dapat diterapkan untuk menyelesaikan masalah tersebut. Akan tetapi, jika solusi yang diperoleh tidak sesuai dengan realita, maka solusi tersebut tidak dapat diterapkan sebagai penyelesaian dari masalah. Dengan demikian kita perlu memperbaiki model matematika yang digunakan dan dicari solusi yang sesuai.

Dalam penelitian ini, terdapat model matematika berupa persamaan gelombang elastis, yaitu

(1.1)

(19)

Variabel merepresentasikan domain ruang satu dimensi dan merepresentasikan waktu. Pada sistem persamaan gelombang elastis di atas, merupakan regangan, merupakan kecepatan, merupakan kepadatan dan merupakan tekanan

Persaman gelombang elastis merupakan model matematika dari permasalahan yang terjadi dalam kehidupan sehari-hari, seperti perambatan gelombang bunyi, getaran gempa bumi, dan sebagainya. Model matematika yang akan diselesaikan dalam penelitian ini adalah masalah khusus dari masalah gelombang elastis, yaitu gelombang akustik. Persamaan gelombang akustik tersebut diturunkan dari (1.1) dan (1.2). Berdasarkan hasil penelitian Supriyadi dan Mungkasi (IJMCE, 14(5), 2016), sistem persamaan (1.1) dan (1.2) dapat diselesaikan dengan menggunakan metode Lax-Friedrichs dan metode LeVeque pada grid kolokasi. Kedua metode tersebut adalah sebagai berikut.

Metode volume hingga Lax-Friedrichs adalah

₍

) (1.3)

Metode volume hingga LeVeque adalah

( ) (1.4)

Di sini , , dan adalah fungsi-fungsi tertentu untuk menghitung fluks material.

(20)

Terdapat dua kajian dalam penelitian ini, yaitu kajian matematika dan pendidikan matematika. Kajian matematika dalam penelitian ini adalah menggunakan metode beda hingga grid selang-seling untuk menyelesaikan persamaan gelombang. Kajian matematika ini merupakan pengembangan dari penelitian yang dilakukan oleh Supriyadi dan Mungkasi (IJMCE, 14(5), 2016). Kajian pendidikan matematika dalam penelitian ini adalah mengetahui kemampuan komunikasi matematik siswa Sekolah Dasar dalam pembelajaran Matematika dengan materi operasi penjumlahan dan pengurangan menggunakan konsep dasar pada kajian matematika, yaitu gelombang elastis.

B. Rumusan Masalah

Berdasarkan latar belakang di atas, rumusan masalah dalam penelitian ini adalah sebagai berikut:

1. Bagaimana menggunakan metode grid selang-seling untuk menyelesaikan persamaan gelombang elastis?

2. Bagaimana kemampuan komunikasi matematik siswa dalam pembelajaran dengan materi operasi penjumlahan dan pengurangan menggunakan konsep gelombang elastis di Sekolah Dasar Gantiwarno?

C. Tujuan Penelitian

Berdasarkan rumusan masalah, tujuan dari penelitian ini adalah sebagai berikut.

(21)

1. Untuk menyelesaikan persamaan gelombang elastis menggunakan metode beda hingga grid selang-seling.

2. Untuk mengetahui kemampuan komunikasi matematik siswa dalam pembelajaran dengan materi operasi penjumlahan dan pengurangan menggunakan konsep gelombang elastis di Sekolah Dasar Negeri 2 Kragilan Gantiwarno.

D. Manfaat Penelitian

Manfaat dari penelitian ini adalah sebagai berikut. 1. Untuk Ilmu Pengetahuan

Penelitian ini dapat melengkapi penelitian sebelumnya, yaitu menyelesaikan persamaan gelombang elastis menggunakan metode beda hingga grid selang-seling. Selain itu, sebagai sumbangan baru terhadap penggunaan metode beda hingga grid selang-seling pada persamaan elastis.

2. Untuk Mahasiswa Jurusan Pendidikan Matematika

Memperkenalkan penggunaan metode beda hingga grid selang-seling dalam menyelesaikan persamaan gelombang elastis, serta penerapan konsep gelombang elastis dalam proses pembelajaran matematika di tingkat sekolah dasar.

3. Untuk Penerapan dalam Kehidupan Sehari-hari

Dapat memperlihatkan penyelesaian masalah yang berkaitan dengan gelombang elastis, misalnya perambatan gelombang suara.

(22)

E. Prasyarat Materi

Untuk memudahkan pembaca dalam memahami penelitian ini, diperlukan beberapa materi prasyarat, yaitu sebagai berikut.

1. Persamaan Diferensial Parsial

Persamaan diferensial parsial merupakan materi yang sering digunakan dalam model-model masalah matematika. Pada penelitian ini, persamaan gelombang elastis berupa persamaan diferensial parsial.

2. Pemodelan Matematika

Tesis ini memuat materi yang berkaitan dengan pemodelan matematika. Masalah-masalah yang akan diselesaikan dalam tesis ini merupakan masalah yang diangkat dari masalah nyata. Masalah nyata tersebut dimodelkan secara matematis agar dapat menentukan solusi dari masalah tersebut.

3. Metode Beda hingga

Metode beda hingga yang digunakan dalam penelitian ini adalah metode beda hingga grid selang-seling.

4. Gelombang

Materi gelombang merupakan materi dasar dari tesis ini. Hal ini dikarenakan masalah yang diangkat dalam tesis ini adalah gelombang elastis, maka diperlukan pengetahuan tentang gelombang untuk memudahkan pembaca dalam memahami tentang gelombang elastis.

(23)

F. Tinjauan Pustaka

Penelitian ini merupakan pengembangan dari penelitian sebelumnya yang diteliti oleh Supryadi dan Mungkasi (2016) untuk menyelesaikan persamaan gelombang elastis nonlinear pada media heterogen. Hasil penelitian tersebut menunjukkan bahwa metode LeVeque dapat menyelesaikan masalah yang berkaitan dengan gelombang elastis, baik linear maupun nonlinear yang melibatkan media heterogen dan homogen. Sedangkan metode Lax-Friedrichs hanya dapat menyelesaikan masalah yang berkaitan dengan gelombang elastis linear dan nonlinear yang melibatkan media homogen saja. Sedangkan pada penelitian dalam tesis ini akan membahas tentang menyelesaikan persamaan gelombang elastis menggunakan metode grid selang-seling.

G. Keterbaruan Penelitian

Pada penelitian sebelumnya, metode Lax-Friedrichs dapat menyelesaikan persamaan elastis linear dan nonlinear yang melibatkan media homogen. Pada penelitian kali ini, akan dicoba metode yang baru yaitu metode beda hingga grid selang-seling untuk menyelesaikan gelombang elastis.

H. Batasan Masalah

Penelitian ini dibatasi pada masalah khusus dari persamaan gelombang elastis, yaitu sistem persamaan akustik, dimana sistem persamaan tersebut merupakan sistem persamaan hiperbolik dari persamaan diferensial parsial linear.

(24)

I. Metode Penelitian

Metode penelitian yang digunakan oleh penulis adalah metode studi pustaka, yaitu mempelajari dan memahami referensi-referensi yang berkaitan dengan metode beda hingga grid selang-seling dan persamaan gelombang elastis, mengumpulkan informasi dan menyusun hasil penelitian menjadi suatu bentuk penulisan yang sistematis dan jelas agar mempermudah pembaca dalam mempelajari masalah dalam penelitian ini. Langkah-langkah yang dilakukan dalam penulisan ini adalah

1. Memahami literatur-literatur yang berkaitan dengan gelombang elastis dan metode Lax-Friedrichs.

2. Mempelajari dan memahami metode beda hingga grid selang-seling. 3. Mempelajari dan memahami persamaan gelombang elastis.

4. Menggunakan metode grid selang-seling untuk menyelesaikan persamaan gelombang elastis.

5. Mensimulasi solusi persamaan gelombang elastis pada komputer.

6. Melakukan penelitian di sekolah untuk perolehan data kemampuan komunikasi matematik di Sekolah Dasar Negeri 2 Kragilan Gantiwarno. 7. Menyusun materi yang telah dipahami secara sistematis untuk

memudahkan pembaca dalam memahami penelitian ini. 8. Mendiskusikan isi tulisan dengan dosen pembimbing.

J. Sistematika Penulisan

(25)

1. Bab I: membahas tentang pendahuluan yang meliputi latar belakang masalah, rumusan masalah, tujuan penelitian, manfaat penelitian, prasyarat materi, tinjauan pustaka, keterbaruan penelitian, batasan masalah, metode penelitian dan sistematika penulisan.

2. Bab II: membahas tentang teori-teori yang digunakan dalam penelitian ini, yaitu persamaan diferensial parsial, penurunan persamaan gelombang, penurunan numeris, persamaan gelombang elastis dan metode beda hingga grid selang-seling.

3. Bab III: membahas hasil penelitian yang berisi tentang model matematika persamaan gelombang elastis, metode numeris grid selang-seling, dan hasil numeris.

4. Bab IV: membahas tentang aspek pendidikan yang berisi tentang kemampuan komunikasi matematik dalam pembelajaran untuk materi operasi penjumlahan dan pengurangan menggunakan konsep gelombang elastis.

(26)

9 BAB II

LANDASAN TEORI

Landasan teori tesis ditulis dalam bab ini. Landasan teori tersebut meliputi: persamaan diferensial parsial, penurunan persamaan gelombang, metode beda hingga grid selang-seling dan persamaan gelombang elastis.

A. Persamaan Diferensial Parsial

Fenomena kontinu, seperti perambatan gelombang atau aliran fluida, umumnya dimodelkan dengan persamaan diferensial parsial (PDP) (Borthwick, 2016). Menurut Wazwaz (2009), persamaan diferensial parsial adalah suatu persamaan yang memuat variabel terikat (fungsi yang belum diketahui), dan turunan parsialnya. Diketahui bahwa pada persamaan diferensial biasa, variabel terikat hanya bergantung pada satu variabel terikat . Akan tetapi, persamaan diferensial parsial, variabel terikatnya, seperti atau

harus bergantung pada lebih dari satu variabel terikat. Jika , maka fungsi bergantung pada variabel terikat dan pada variabel

waktu . Namun, jika , maka fungsi bergantung pada variabel ruang dan pada variabel waktu .

Salah satu contoh persamaan diferensial parsial adalah sistem persamaan untuk masalah akustik, yaitu:

(2.1)

(27)

dengan merepresentasikan kecepatan perambatan gelombang, merepresentasikan tekanan, merepresentasikan domain ruang dan merepresentasikan domain waktu.

B. Penurunan Persamaan Gelombang

Persamaan gelombang diturunkan dari hukum kekekalan massa dan hukum kekekalan momentum (hukum kedua Newton). Dipandang hukum kekekalan massa adalah sebagai berikut.

(2.3) dengan adalah massa volume , dan merupakan waktu. Menggunakan kepadatan , hukum kekekalan massa dapat ditulis dalam bentuk berikut, agar memperoleh bentuk eksplisit, diasumsikan , sehingga (2.4) menjadi

(2.4)

(2.5) Dengan mengabaikan , maka (2.5) menjadi,

Sehingga diperoleh (2.6)

(28)

Akan diturunkan suatu persamaan dengan tekanan di dalamnya, sehingga diasumsi terdapat relasi linear antara tekanan dan kepadatan , maka menggunakan modulus bulk dengan mempertimbangkan massa satuan, yaitu:

(2.7)

dengan merupakan modulus bulk dan adalah tekanan. Berdasarkan (2.7), diperoleh perubahan tekanan, yaitu:

(2.8)

Lalu (2.8) dapat ditulis menjadi,

(2.9)

yang merumuskan hukum Hooke. Sekarang, akan diasumsi perubahan volume hanya pada satu dimensi.

(2.10)

Karena merupakan perbedaan antara perpindahan pada sisi-sisinya, maka

(2.11) (2.12)

dimana merupakan kecepatan partikel pada arah . Berdasarkan (2.12) diperoleh

(29)

(2.13)

Kemudian, (2.13) disubstitusi ke persamaan hukum Hooke, sehingga diperoleh

(2.14) atau (2.15)

yang merupakan hubungan dasar untuk penurunan persamaan gelombang.

Relasi lainnya diperoleh melalui hukum Newton yang diterapkan pada volume dengan arah , karena dipertimbangkan gerakan satu dimensi

(2.16)

dimana merupakan gaya yang bekerja pada . Dengan mempertimbangkan gaya pada arah- :

(2.17) ( ) (2.18) (2.19)

Mengabaikan syarat karena sangat kecil, dan merupakan permukaan pada arah- . Substitusi (2.19) ke dalam hukum Newton, sehingga diperoleh:

(30)

Pada persamaan,

dapat ditulis sebagai

, untuk itu digunakan lagi pendekatan kecepatan rendah, yaitu:

(2.21) Sehingga, (2.20) menjadi, (2.22) atau (2.23)

yang merupakan persamaan gerak.

Tahap selanjutnya adalah menggabungkan hukum kekekalan massa dan persamaan gerak. Oleh karena itu, (2.23) diturunkan secara parsial terhadap , sehingga ( ) ( ) (2.24) ( ) ( ) (2.25)

dengan adalah konstanta. Substitusi (2.15) ke dalam (2.25), sehingga diperoleh

( ) (2.26) (2.27) (2.28)

(31)

atau

(2.29)

yang merupakan persamaan gelombang satu dimensi dengan dapat dipandang

sebagai kecepatan, √ .

C. Penurunan Numeris

Tidak semua fungsi dapat dengan mudah dihitung nilai turunannya secara analitik. Oleh karena itu, diperlukan metode numeris untuk menghitung nilai turunan fungsi yang bentuknya cukup rumit, misalnya:

√ (2.30) Untuk fungsi yang rumit ini, turunannya dapat ditentukan secara numeris. Turunan numeris ini diperoleh dengan pendekatan deret Taylor. Berikut ini tiga hampiran turunan numeris.

1. Turunan beda maju

Dipandang deret Taylor di sekitar titik adalah

(2.31)

Kedua ruas dikurangi , menjadi

(2.32)

(32)

(2.33)

Maka

(2.34)

Sehingga diperoleh turunan beda maju adalah

(2.35)

Dengan

(2.36)

2. Turunan beda mundur

Dipandang deret Taylor di sekitar titik adalah

(2.36) (2.37) (2.38)

(33)

(2.39)

Sehingga diperoleh turunan beda mundur sebagai berikut

(2.40)

dengan

(2.41)

3. Turunan beda pusat

Turunan beda pusat diperoleh dari pengurangan deret Taylor yang digunakan pada turunan beda maju dan turunan beda mundur, yaitu (2.31) dan (2.36) sehingga diperoleh:

(2.42)

Kedua ruas pada (2.42) dibagi , maka diperoleh

(2.43) Atau (2.43) Jadi (2.44)

(34)

dengan

(2.45)

D. Persamaan Gelombang Elastis

Gelombang elastis merupakan gelombang yang perambatannya tergantung pada sifat media perambatan itu sendiri, misalnya, gelombang suara (akustik). Contoh kasus gelombang akustik yang sering dijumpai dalam kehidupan sehari-hari adalah kegiatan berbicara dengan teman atau orang lain. Ketika kita berbicara dengan teman atau orang yang berada pada ruangan yang sama, suara kita akan terdengar dengan jelas. Akan tetapi, jika berbicara dengan teman atau orang yang berada pada ruangan yang berbeda, maka tingkat kejelasan suara yang sampai ke telinga akan menurun. Hal ini disebabkan oleh media rambatan suara tersebut.

Pada saat berbicara dengan teman atau orang yang berada pada satu ruangan, media rambatan yang dilibatkan hanya udara dan benda-benda yang berada di ruangan tersebut. Sehingga suara yang sampai ke telinga akan terdengar lebih jelas. Lain halnya ketika berbicara dengan teman atau orang yang berada pada ruangan yang berbeda. Media rambatan yang dilibatkan akan lebih banyak, misalnya udara, dinding pembatas ruangan dan atap ruangan. Keadaan ini mengakibatkan tingkat kejelasan suara yang sampai ke telinga lebih rendah. Berkaitan dengan gelombang elastis, kedua kasus ini memperlihatkan bahwa jumlah media perambatan gelombang akustik mempengaruhi gelombang yang dihantarkan. Semakin banyak media rambatnya maka kepadatan atau massa jenis

(35)

semakin tinggi, sehingga mempengaruhi kecepatan dan besar kecilnya gelombang tersebut.

Secara umum, bentuk hukum kekekalan yang digunakan adalah pada penelitian ini adalah

(2.46) dengan merupakan variabel waktu, merupakan variabel ruang, yang merupakan kuantitas kekekalan, dan ( ) merupakan fungsi fluks (Supriyadi dan Mungkasi, 2016). Persamaan umum gelombang elastis yang digunakan dalam penelitian ini adalah sebagai berikut (LeVeque, 2002b).

(2.47)

(2.48) dimana, (2.47) dan (2.48) merupakan bentuk konservatif untuk masalah non-linear. Variabel merepresentasikan domain ruang satu dimensi dan merepresentasikan waktu. Pada sistem persamaan gelombang elastis di atas,

merupakan regangan, merupakan kecepatan, merupakan

kepadatan dan merupakan tekanan.

Sistem persamaan (2.47) dan (2.48) merupakan bentuk persamaan diferensial parsial, dengan mengasumsikan terdapat relasi antara dan . Persamaan diferensial parsial tersebut bisa menjadi bentuk persamaan akustik linear pada satu dimensi ruang yang merupakan kasus khusus dari gelombang elastis.

(36)

E. Metode Beda Hingga Grid Selang-seling

Metode beda hingga merupakan salah satu metode numerik untuk menentukan solusi persamaan diferensial. Dalam menentukan solusi dari persamaan diferensial tersebut, metode ini menggunakan hampiran. Hampiran tersebut digunakan untuk menentukan fungsi atau pendekatan diskrit yang memenuhi persamaan diferensial yang diselesaikan. Terdapat beberapa hampiran metode beda hingga, yaitu sebagai berikut.

Dipandang

(2.49) dengan domain dan ,

dengan dengan

Maka, metode beda maju terhadap waktu adalah

| (2.50)

dan metode beda pusat terhadap waktu adalah

| (2.51) dengan .

Misalkan akan diselesaikan masalah persamaan diferensial parsial

(37)

untuk domain .

Menggunakan metode beda hingga, domain tersebut didiskritkan sebagai berikut.

Secara notasi, dengan dan

Misalkan diambil diskritisasi dengan beda maju terhadap waktu, sehingga skema menjadi:

(2.53)

dan diskritisasi dengan beda mundur terhadap dimensi, sehingga skema menjadi

(2.54)

maka diskritisasi menjadi

(2.55)

dengan menjumlahkan kedua ruas dengan

, maka (2.55) menjadi (2.56)

Lalu kedua ruas dikali menjadi,

(38)

( )

(2.57)

Selanjutnya menjumlahkan kedua ruas dengan , diperoleh

( )

(2.58)

Skema (2.58) merupakan skema beda hingga dari .

Berkaitan dengan metode beda hingga selang-seling, metode ini merupakan metode numerik yang mengatur diskretisasi ruang dengan variabel-variabelnya pada sel atau grid yang berbeda. Manfaat utama metode ini adalah metode ini tidak menghasilkan perhitungan tekanan dan kecepatan secara terpisah. Pada penelitian ini, metode tersebut digunakan untuk menyelesaikan persamaan gelombang elastis dengan domain dan .

Beda hingga selang-seling yang dimaksudkan dalam metode ini adalah menyelesaikan sistem persamaan gelombang elastis pada grid yang berbeda. Pada rumusan selang-seling, nilai tekanan ditentukan pada titik grid penuh sedangkan kecepatan ditentukan pada titik grid setengah. Berikut ini adalah diskritisasi domain metode beda hingga grid selang-seling.

(39)

22 BAB III

HASIL PENELITIAN

A. Model Matematika Persamaan Gelombang Elastis

Bentuk umum persamaan gelombang elastis satu dimensi adalah

(3.1)

( ) (3.2) Variabel bebas merepresentasikan domain ruang dan merepresentasikan waktu. Sebagai tambahan, merupakan regangan, merupakan kecepatan, merupakan densitas, dan merupakan tegangan. Perhatikan bahwa

. Notasi turunan lainnya diartikan secara senada.

Dalam persamaan (3.1) dan (3.2), tegangan dan regangan diasumsi memiliki relasi

(3.3) dengan adalah modulus bulk kompresibilitas. Tekanan , sehingga persamaan (3.1) dan (3.2) dapat ditulis dalam bentuk persamaan diferensial parsial linear

(3.4)

(3.5) Diasumsi, dan , sehingga persamaan (3.4) dan (3.5) dapat ditulis sebagai berikut

_{Hasil penelitian ini telah dipresentasikan dalam International Conference on Science and Applied}

Science (ICSAS 2017) di Surakarta pada tanggal 29 Juli 2017. Hasil ini telah terbit dalam Journal of Physics: Conference Series 909 (2017) 012047.

(40)

(3.6)

(3.7)

Sistem persamaan (3.6) dan (3.7) merupakan sistem hiperbolik dari persamaan diferensial parsial. Pada bagian selanjutnya, akan fokus pada pemecahan sistem persamaan (3.6) dan (3.7) yang merupakan model untuk masalah akustik.

B. Metode Numeris Grid Selang-seling Diketahui bahwa (3.8) (3.9)

Diambil diskritisasi dari bentuk derivatifnya

(3.10) (3.11)

Menggunakan pendekatan (3.10) dan (3.11), persamaan (3.6) dapat ditulis dalam bentuk diskrit sebagai berikut

( ) (3.12)

Selanjutnya, menggunakan diskritisasi dari turunan berikut

(3.13)

(3.14)

(41)

Menggunakan pendekatan (3.13) dan (3.14), bentuk diskret dari persamaan (3.7) adalah

₍ ) (3.15) Sistem persamaan (3.12) dan (3.15) merupakan skema numeris, untuk menyelesaikan masalah akustik.

C. Hasil Numeris

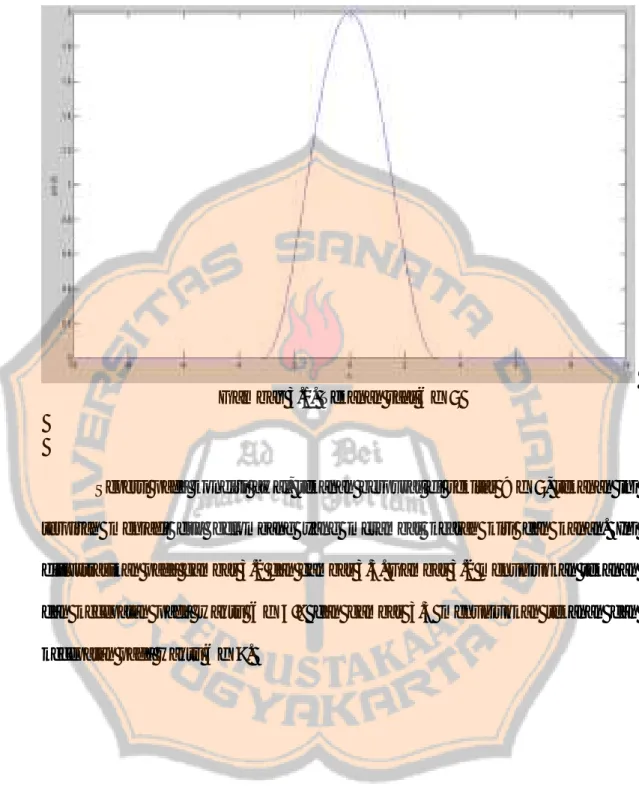
Pada bagian ini dikhususkan untuk menyajikan hasil numeris. Asumsi awalnya adalah masalah akustik memiliki fungsi tekanan

{ (3.16)

Untuk . Tekanan awal ini ditunjukkan pada gambar 3.1. Kecepatan awalnya adalah untuk setiap domain ruang.

Dengan menggunakan data yang diberikan, domain ruang adalah [ dengan . Akan dihitung tekanan dan kecepatan dalam sistem setiap saat. Jumlah ruang yang digunakan adalah , dan

(42)

Gambar 3.1. Tekanan saat

Seperti pada kondisi awal, tekanan berpusat di sekitar , tekanan ini terpisah menjadi dua gelombang yang merambat kearah kiri dan kanan. Ini diilustrasikan pada gambar 3.2 dan gambar 3.3. Gambar 3.2 menunjukkan tekanan dan kecepatan pada waktu dan gambar 3.3 menunjukkan tekanan dan kecepatan pada waktu .

(43)

Gambar 3.2. Tekanan saat

(44)

Berdasarkan hasil simulasi, metode beda hingga pada grid selang-seling telah diturunkan dan digunakan untuk memecahkan masalah persamaan gelombang elastis yang berkaitan dengan masalah akustik. Dalam penelitian ini, pengujian menggunakan nilai awal yang halus (smooth). Diperoleh perilaku fisik yang benar dalam solusi numeris karena ada satu gelombang tekanan tunggal dengan kecepatan nol, tekanannya terbagi menjadi dua dan bergerak berlawanan arah seiring berjalannya waktu.

(45)

A. Teori Perkembangan Piaget

Pandangan Piaget tentang perkembangan kognitif sangat dipengaruhi oleh pengalamannya di bidang biologi. Oleh karena itu, konsep dasar perkembangan belajarnya adalah konsep biologis yakni adaptasi (Piaget, 1971 dalam Berk, 2012). Adapun tahap perkembangan kognitif menurut Piaget antara lain:

1. Tahap sensoris motorik (Lahir-2 tahun)

Pada tahap ini individu (bayi) “berpikir” dengan merespons dunia

melalui mata, telinga, mulut mereka. Mereka menemukan cara penanggulangan persoalan sensoris motorik seperti menggunakan indra dan gerak untuk mengeksplorasi dunia. Pada tahap ini penanggulangan persoalan mereka adalah seperti mencari barang yang hilang dan menaruh mengeluarkan objek dari tempatnya. Tahapan ini dimulai dari tindakan refleks naluriah sampai dengan permulaan pemikiran simbolis (Berk, 2012).

2. Tahap pra-operasional (sekitar 2-7 tahun)

Pada tahap ini anak mampu melukiskan dunia dengan simbol, kata-kata dan gambar untuk mewakili temuan sensoris-motoriknya. Namun, pada tahap ini pemikiran mereka belum melibatkan logika (Berk, 2012).

(46)

3. Tahap Operasional Konkret (sekitar 7-11 tahun).

Pada tahap ini, penalaran anak-anak mulai logis. Namun, pemikiran logis dan teratur ini hanya sebatas pada informasi konkret yang mereka terima secara langsung (Berk, 2012).

4. Tahap Operasional Formal (11 tahun ke atas)

Kemampuan berpikir abstrak dan sistematis membantu remaja mampu membuat hipotesis, mengambil kesimpulan teruji, dan memisahkan serta menggabungkan variabel-variabel untuk melihat kesimpulan mana yang benar (Berk, 2012). Remaja juga mampu mengevaluasi logika di balik pernyataan verbal tanpa mengacu pada keadaan di dunia nyata.

B. Komunikasi Matematik

Menurut Romberg dan Chair yang dikutip oleh Sumarmo (dalam Rachmayani, 2014), komunikasi matematika yaitu menghubungkan benda nyata, gambar dan diagram ke dalam ide matematika; menjelaskan ide, situasi dan relasi matematik secara lisan atau tulisan dengan benda nyata, gambar, grafik dan aljabar; menyatakan peristiwa sehari-hari dalam bahasa atau simbol matematika; mendengarkan, berdiskusi dan menulis tentang matematika; membaca dengan pemahaman suatu presentasi matematika tertulis, membuat konjektur, menyusun argumen, merumuskan definisi dan generalisasi; menjelaskan dan membuat pertanyaan tentang matematika yang telah dipelajari.

(47)

Indikator kemampuan komunikasi matematik yang digunakan dalam penelitian ini adalah indikator-indikator menurut National Council of Teachers of Mathematics (2000), sebagai berikut:

a. Kemampuan mengekspresikan ide-ide matematis melalui, tulisan dan mendemonstrasikannya serta menggambarkannya secara visual

b. Kemampuan memahami, menginterpretasikan dan mengevaluasi ide-ide matematis baik secara lisan, tulisan, maupun dalam bentuk visual lainnya c. Kemampuan dalam menggunakan istilah-istilah, notasi-notasi matematika

dan struktur-strukturnya untuk menyajikan ide-ide, menggambarkan hubungan-hubungan dengan model-model situasi

C. Hasil Penelitian dan Analisis

Penelitian ini dilaksanakan pada tanggal 25 Oktober 2017, di SD Negeri 2 Kragilan Gantiwarno, Klaten, kelas VI dengan jumlah siswa 18 orang. Sebelum penelitian dilaksanakan, peneliti memulai kegiatan dengan memberikan penjelasan singkat tentang tujuan kegiatan pembelajaran yang akan dilaksanakan. Selain itu, peneliti memberikan beberapa pertanyaan yang berkaitan dengan gelombang elastis, agar siswa memiliki gambaran tentang gelombang elastis selama kurang lebih 15 menit.

Sebelum masuk pada kegiatan inti, peneliti membagi siswa dalam 2 kelompok dan setiap kelompok terdiri dari 9 siswa. Kedua kelompok tersebut diberikan alat peraga yang akan digunakan selama penelitian. Selain alat peraga, setiap anggota kelompok juga diberikan satu lembar LKS yang memuat

(48)

langkah-langkah penggunaan alat peraga dan 10 soal yang berkaitan dengan materi operasi penjumlahan dan pengurangan. Kemudian, kedua kelompok tersebut menyelesaikan soal-soal yang diberikan dengan bantuan alat peraga. Waktu yang digunakan untuk menyelesaikan soal-soal tersebut adalah 45 menit.

Selama proses penyelesaian soal-soal, siswa dibimbing dan diarahkan oleh peneliti, sehingga proses penyelesaian berjalan dengan baik. Setelah menyelesaikan soal-soal, peneliti mengumpulkan hasil kerja siswa. Sebagai kegiatan penutup, peneliti mengajukan pertanyaan dan membuat kesimpulan dari kegiatan yang telah dilakukan siswa selama 10 menit. Selain itu, peneliti juga memperkenalkan penelitian matematika yang dilakukan peneliti kepada siswa dengan cara mengkaitkan kegiatan sebelumnya dengan konsep dasar penelitian matematika tersebut.

Data penelitian yang diperoleh berupa Lembar Kerja Siswa (LKS) dan video kegiatan pembelajaran. Soal-soal yang terdapat pada LKS akan dianalisis berdasarkan indikator-indikator komunikasi matematik menurut NCTM. Video pembelajaran merupakan data pendukung untuk memperkuat pendapat peneliti tentang informasi yang terdapat pada LKS. Data berupa video tersebut disalin menjadi percakapan. Berikut ini hasil dan analisis data-data tersebut.

(49)

33 Tabel 4.1 Hasil kerja dan Wawancara serta Analisis dan Pembahasan

Hasil Kerja dan Wawancara Siswa Analisis dan Pembahasan Indikator Soal: Siswa mampu mengukur waktu menggunakan stopwatch (soal 1-4) K1

Soal 1: berapa lama kawat tersebut bergetar?

(Gambar 4.1.1. Hasil pekerjaan Siswa untuk soal 1) Transkrip video

K1a : ci.. ro… lu… stop… sekk… sek…

P : awas kena rambut, dicoba lagi.. K1a : ci… ro… lu…sek… sek….Stooop….

Piro? K1b : 22 detik

Soal 2: berapa lama benang tersebut bergetar?

(Gambar 4.1.2. Hasil pekerjaan siswa untuk soal 2)

1. Kemampuan dalam menggunakan istilah-istilah, notasi-notasi matematika untuk menyajikan ide.

Berdasarkan hasil pekerjaan pada gambar 4.1.1. sampai gambar 4.1.8., K1 dan K2 sudah mampu menggunakan istilah dan notasi matematika untuk menyajikan ide, yaitu:

 Kemampuan menggunakan istilah dapat dilihat dari

penggunaan kata satuan waktu, yaitu detik

 Kemampuan menggunakan notasi matematika untuk

menyajikan ide dilihat dari penggunaan angka, misalnya

“22”, “3”, “9”, “36”, “19”, “4”, “10” dan “37”.

2. Kemampuan memahami, menginterpretasikan baik secara lisan, tulisan maupun dalam bentuk visual lainnya.

(50)

34 Soal 3: berapa lama senar tersebut bergetar?

dapat menginterpretasikan baik secara lisan, tulisan maupun dalam bentuk visual lainnya.

 Kemampuan memahami dapat dilihat dari proses

penyelesaian soal, dimana K1 dan K2 menggunakan media pembelajaran yang ada untuk menemukan penyelesaian masalah.

 Kemampuan menginterpretasikan dapat dilihat dari penulisan “22 detik”, “3 detik”, “9 detik, “36 detik”, “19 detik”, “4 detik”, “10 detik” dan “37 detik” yang

merupakan waktu kawat dimana jawaban tersebut merupakan hasil dari pengukuran waktu getaran menggunakan media pembelajaran yang telah disediakan.

3. Kemampuan mendemonstrasikan serta menggambarkan melalui lisan dan tulisan

Berdasarkan proses penyelesaiannya, K1 dan K2 sudah mampu mendemonstrasikan kegiatan praktikum dengan baik dan sesuai instruksi pada soal.

K2

Soal 1: berapa lama kawat tersebut bergetar?

(Gambar 4.1.5. Hasil pekerjaan siswa untuk soal 1) Transkrip Video

P : Satu, dua, tiga, yaps…. Lihat ya,…. K2 : kosekk…seeekk.. sekkk…. Yaaa..

P : ok, jadi itu berapa? (sambil menunjuk pada stopwatch)

K1 : Sembilan belas

(51)

35 K1 : Sembilan belas

P : Sembilan belas de….?

K1 :19 detik. (sambil menulis jawaban di LKS)

Soal 2: berapa lama benang tersebut bergetar?

Soal 3: berapa lama senar tersebut bergetar?

Soal 4: berapa lama karet tersebut bergetar?

(52)

36 Indikator soal: siswa mampu menjelaskan sifat elastisitas gelombang (Soal 5)

K1

Soal 5: Benda manakah yang lebih lama bergetar? Menurutmu mengapa benda tersebut lama bergetar?

(Gambar 4.1.9. hasil pekerjaan siswa untuk soal 5)

Soal ini merupakan bentuk soal penalaran fisika, dimana jawaban pada gambar 4.1.9 sampai gambar 4.1.10 berdasarkan fenomena hasil percobaan yang diperoleh K1 dan K2. Pada hasil pekerjanya, kedua kelompok menjawab pertanyaan dengan benar.

Berdasarkan pengamatan peneliti, jawaban K1 dan K2 di peroleh dari pengamatan dan percobaan terhadap fenomena yang terjadi ketika diberi perlakuan pada setiap benda yang digunakan selama kegiatan percobaan tersebut.

Dengan demikian, untuk soal 5 ini, tidak dapat digunakan untuk menganalisis jawaban soal 5.

K2

Soal 5: Benda manakah yang lebih lama bergetar? Menurutmu mengapa benda tersebut lama bergetar?

(53)

37 Indikator soal: siswa dapat menerapkan operasi pengurangan (soal 6-7)

K1

Soal 6: berapa perbedaan waktu bergetar antara kawat dan benang?

(Gambar 4.1.11. Hasil pekerjaan siswa soal 6)

Soal 7: berapa perbedaan waktu bergetar antara karet dan senar?

1. Kemampuan dalam menggunakan istilah-istilah, notasi-notas matematika untuk menyajikan ide.

Pada soal 6-7, K1 sudah mampu dalam menggunakan istilah-istilah, notasi-notasi matematika untuk menyajikan ide-ide.

• Kemampuan menggunakan istilah dapat dilihat dari penggunaan kata “detik” pada hasil kerja K1.

• Kemampuan menggunakan notasi matematik dilihat dari

penggunaan notasi operasi pengurangan (-) seperti pada gambar 4.1.11. sampai gambar 4.1.12.

Pada soal 6-7, K1 cukup mampu menggunakan kemampuan memahami menginterpretasikan baik secara lisan, tulisan, maupun dalam bentuk visual lainnya.

(54)

38

• Kemampuan memahami masalah dilihat dari penggunaan

operasi hitung yang tepat untuk menyelesaikan masalah. Akan tetapi, pada pekerjaan siswa, tidak tertulis informasi yang diketahui dan tujuan masalah yang akan dicapai.

• Kemampuan menginterpretasikan secara tulisan dilihat

dari pekerjaan siswa dimana siswa menggunakan operasi pengurangan secara bersusun.

3. Kemampuan mendemonstrasikan serta menggambarkan melalui lisan dan tulisan.

Berdasarkan kegiatan praktik dan proses penyelesaiannya, K1 mampu mendemonstrasikan masalah yang diberikan, dimana siswa mengukur waktu yang dibutuhkan setiap benda untuk bergetar. Kemudian siswa menuliskannya dalam bentuk angka dan dilengkapi dengan satuan waktu berdasarkan hasil pengukuran tersebut.

(55)

39 K2

Soal 6: berapa perbedaan waktu bergetar antara kawat dan benang?

(Gambar 4.1.13. Hasil pekerjaan siswa 6)

Soal 7: berapa perbedaan waktu bergetara antara karet dan senar?

1. Kemampuan dalam menggunakan istilah-istilah, notasinotasi matematika untuk menyajikan ide.

Berdasarkan hasil kerja pada gambar 4.1.13 sampai gambar 4.1.14, K2 mampu menggunakan istilah-istilah, notasi-notasi matematika untuk menyajikan ide.

• Kemampuan menggunakan istilah-istilah seperti “kawat 19 detik”, “benang 4 detik”, “karet 37 detik” dan “senar 10 detik”.

• Kemampuan menggunakan notasi matematik seperti

menggunakan notasi operasi pengurangan (-), dengan proses pengurangan secara bersusun.

Berdasarkan hasil kerja pada gambar 4.1.13 sampai gambar 4.1.14., K2 cukup mampu memahami, menginterpretasikan baik secara lisan, tulisan maupun dalam bentuk visual lainnya.

(56)

40

• Kemampuan memahami dilihat dari penyelesaian

masalah siswa dimana siswa menggunakan operasi hitung pengurangan untuk menyelesaikan masalah.

• Kemampuan menginterpetasikan secara tulisan dilihat

dari proses penyelesaian siswa menggunakan operasi hitung pengurangan secara bersusun. Akan tetapi, terdapat beberapa informasi yang ditulis kurang jelas dalam pekerjaannya.

Berdasarkan proses penyelesaian masalah, K2 sudah mampu mendemonstrasikan serta menggambarkan melalui lisan dan tulisan. Hal ini dilihat dari proses penyelesaian masalah, dimana K2 melaksanakan setiap instruksi praktik untuk memperoleh data. Lalu data yang diperoleh ditulis menggunakan angka dan satuan waktu.

(57)

41 Indikator soal: siswa dapat menerapkan operasi penjumlahan (soal: 8-10)

K1

Soal 8:berapa total waktu kawat dan benag untuk bergetar?

Soal 9: berapa total waktu karet, benang dan kawat untuk bergetar?

Berdasarkan hasil kerja pada gambar 4.1.15 sampai gambar 4.1.17 disamping, K1 sudah mampu menggunakan istilah-istilah, notasi-notasi matematika untuk menyajikan ide.

 Kemampuan menggunakan istilah, terlihat dari

penggunaan satuan detik.

 Kemampuan menggunakan notasi matematika dilihat

dari penggunaan notasi operasi penjumlahan (+).

Berdasarkan hasil pekerjaan pada gambar 4.1.15 sampai gambar 4.1.17., K1 cukup mampu memahami, menginterpretasikan baik secara lisan, tulisan maupun dalam bentuk visual lainnya.

(58)

42 Soal 10: berapa total waktu karet, benang, senar

dan kawat untuk bergetar?

• Kemampuan memahami dapat dilihat dari pemilihan

metode penyelesaian masalah, dimana siswa menggunakan operasi penjumlahan untuk menentukan total waktu bergetar dari setiap benda yang ditanya.

• Kemampuan menginterpretasikan dilihat dari penulisan

siswa untuk menyelesaikan operasi penjumlahan, dimana siswa menggunakan penjumlahan bersusun untuk menyelesaikan masalah. Akan tetapi, pada proses penyelesaiannya siswa tidak menuliskan keterangan yang diketahui dan tujuan penyelesaian masalah.

Berdasarkan hasil pekerjaan pada gambar 4.1.15 sampai gambar 4.1.17.,, K1 sudah mampu mendemonstrasikan serta menggambarkan melalui tulisan mengenai penyelesaian masalah.

K2

Soal 8: berapa total waktu kawat dan benag untuk bergetar?

(59)

43 (Gambar 4.1.18. Hasil pekerjaan siswa soal 8)

Soal 9: berapa total waktu karet, benang dan kawat untuk bergetar?

4.1.20., K2 sudah mampu menggunakan istilah-istilah, notasi-notasi matematika untuk menyajikan ide.

• Kemampuan menggunakan istilah-istilah dilihat dari

penyelesaian K2 menerangkan waktu yang dibutuhkan setiap benda untuk bergetar. Selain itu siswa juga menggunakan istilah detik sebagai satuan waktu.

• Kemampuan menggunakan notasi-notasi matematika

dilihat dari penggunaan notasi operasi penjumlahan (+) pada pekerjaan siswa.

Berdasarkan hasil kerja pada gambar 4.1.18 sampai gambar 4.1.20., K2 sudah mampu memahami, menginterpretasikan baik secara tulisan.

• Kemampuan memahami dilihat dari pemilihan metode

untuk menyelesaikan masalah, yaitu operasi penjumlahan.

(60)

44 Soal 10: berapa total waktu karet, benang, senar

dan kawat untuk bergetar?

• Kemampuan menginterpretasikan dilihat dari tulisan

siswa, dimana siswa dapat menginterpretasikan masalah dalam bahasa matematika. Akan tetapi bahasa matematika pada tulisan tersebut belum tepat.

Berdasarkan hasil kerja pada gambar 4.1.18 sampai gambar 4.1.20., K2 sudah mampu mendemonstrasikan serta menggambarkan melalui tulisan.

Hal ini dilihat dari teknik yang digunakan siswa, yaitu teknik penjumlahan bersusun untuk memudahkan siswa dalam berhitung.

Keterangan:

 K1: kelompok 1  K2: kelompok 2

(61)

45 Berdasarkan analisis dan pembahasan pada tabel 4.1 di atas, K1 belum sepenuhnya mampu memenuhi ketiga indikator NCTM tersebut secara tulisan karena belum memenuhi indikator kedua untuk soal 6 sampai soal 10. K1 cenderung untuk langsung menggunakan metode penyelesaian yang cocok tanpa menerangkan terlebih dahulu informasi dan tujuan dari soal tersebut. Selain itu, K2 sudah memenuhi ketiga indikator kemampuan komunikasi matematik meskipun terdapat sedikit kekurangan dalam penulisan informasi dalam menyelesaikan soal-soal yang diberikan.

(62)

46 D. REFLEKSI

Selama kurang lebih 2 tahun berdinamika, belajar bersama teman-teman dan para Dosen S2 Pendidikan Matematika Sanata Dharma, hal yang paling menantang dan sangat berkesan adalah proses penyusunan tesis. Suka dan duka pun mengiringi proses penuh tantangan ini. Salah satu tantangan terberat selama proses penyelesaian tesis ini adalah mengalahkan diri sendiri. Terdapat beberapa sikap yang muncul, seperti malas, jenuh dan putus asa. Dibutuhkan usaha yang cukup untuk mengatasi keadaan itu untuk kembali melanjutkan pekerjaan yang belum selesai.

Hal yang dapat saya jadikan pelajaran hidup selama proses menyelesaikan

tesis ini adalah “jangan menunda pekerjaan, selesaikan sampai tuntas”. Saya

seringkali mengalami kesusahan karena kebiasaan saya yang selalu menunda untuk menyelesaikan suatu pekerjaan. Akibatnya, saya tidak dapat mencapai target saya. Berbagai hal yang telah saya rencanakan pun tidak terlaksana dengan baik.

Harapan saya untuk tahap selanjutnya, saya harus lebih rajin dan meninggalkan kebiasaan lama saya, agar dapat mencapai target dan semua rencana dapat terlaksana dengan baik.

(63)

47 BAB V PENUTUP

Pada bagian ini akan membahas tentang kesimpulan dari penelitian yang telah dilaksanakan, baik penelitian matematika maupun penelitian pendidikan matematika. Selain itu, pada bab ini pula membahas tentang saran bagi pengembangan penelitian selanjutnya.

A. Kesimpulan

Berdasarkan penelitian dan hasil pembahasan, maka dapat disimpulkan bahwa: 1. Metode grid selang-seling dapat digunakan untuk menyelesaikan persamaan

gelombang elastis yang berkaitan dengan masalah akustik. Pada penelitian ini, peneliti menggunakan masalah nilai awal yang halus (smooth).

2. Pada solusi numeris, diperoleh perilaku fisik yang tepat karena terdapat 1 gelombang tekanan dengan kecepatan nol, tekanan terbagi menjadi 2 bagian dan bergerak menuju arah yang berlawanan seiring berjalannya waktu.

3. Berdasarkan pembelajaran matematika yang dilakukan untuk materi operasi penjumlahan dan pengurangan menggunakan konsep gelombang elastis di kelas VI SD Negeri 2 Kragilan Gantiwarno tahun 2017, kemampuan komunikasi matematik dari 18 siswa di kelas dalam menyelesaikan soal yang diberikan adalah sebagai berikut:

a. Terdapat 9 siswa sudah mampu memenuhi 2 indikator NCTM, yaitu indikator kemampuan dalam menggunakan istilah-istilah, notasi-notasi matematika untuk menyajikan ide dan indikator kemampuan

(64)

a. mendemonstrasikan serta menggambarkan melalui lisan dan tulisan mengenai konsep operasi penjumlahan dan pengurangan.

b. Terdapat 9 siswa sudah memenuhi ketiga indikator NCTM, yaitu indikator kemampuan dalam menggunakan istilah-istilah, notasi-notasi matematika untuk menyajikan ide, indikator kemampuan memahami menginterpretasikan secara lisan, tulisan maupun dalam bentuk visual lainnya, dan indikator kemampuan mendemonstrasikan serta menggambarkan melalui lisan dan tulisan mengenai materi operasi penjumlahan dan pengurangan, meskipun terdapat sedikit kekurangan dalam penulisan informasi dalam menyelesaikan soal.

B. Saran

Sebagai bentuk dukungan perkembangan bagi penelitian selanjutnya, peneliti menyarankan untuk meneliti kinerja metode beda hingga grid selang-selang terhadap masalah-masalah kasar (nonsmooth). Selain itu, untuk pengembangan penelitian dalam bidang pendidikan matematika, disarankan untuk menggunakan soal-soal yang lebih konstekstual, sehingga selain mengukur kemampuan komunikasi matematik siswa, juga dapat mengukur kemampuan penalaran siswa. Selain itu, diharapkan pada penelitian selanjutnya untuk menggunakan metode wawancara untuk memperkuat analisis data.

(65)

49

DAFTAR PUSTAKA

Ansari, dkk, 2016, Komunikasi Matematik, Strategi Berpikir dan Manajemen Belajar: Konsep dan Aplikasi, PeNA, Banda Aceh.

Bartolo, L.D., Dors, C. dan Mansur, W.J., 2015, Theory Of Equivalent Staggered-Grid Schemes: Application To Rotated And Standard Staggered-Grids In Anisotropic Media, Geophysical Prospecting, 63, 1097.

Berk, L.E., 2012, Development Trought The Lifespam, Pustaka Pelajar, Yogyakarta.

Borthwick, D., 2016, Introduction To Partial Differential Equations, Springer, USA.

Breuss, M., 2004, The Correct Use of The Lax-Friedrichs Method, http://www.esaim-m2an.org/articles/m2an/pdf/2004/03/m2an0383.pdf/ Diakses 7 Januari 2018.

Dettmer, W.G. dan Peric, B., 2013, A New Staggered Scheme For Fluid-Structure Interaction, International Journal for Numerical Methods in Engineering, 93, 1.

Hall, F. dan Wang, Y., 2009, Elastic Wave Modelling By An Integrated Finite Difference Method, Geophysical Journal International, 177, 104.

Huang, C. dan Dong, L-G., 2009, Staggered-Grid High-Order Finite-Difference Method In Elastic Wave Simulation With Variable Grids And Local Time-Steps, Chinese Journal of Geophysics, 52, 1324.

Lee, J.J. dan Kim, H.H., 2016, Analysis Of A Staggered Discontinuous Galerkin Method For Linear Elasticity, Journal of Scientific Computing, 66, 625. LeVeque, R.J., 2002a, Finite Volume Methods for Hyperbolic Problems,

Cambridge University Press, Cambridge.

LeVeque, R.J., 2002b, Finite-Volume Methods For Non-Linear Elasticity In Heterogeneous Media, International Journal for Numerical Methods in Fluids, 40, 93.

Mungkasi, S. dan Ningrum, G.I.J., 2016, Numerical Solution To The Linear Acoustics Equations, AIP Conference Proceedings, 1746, 020056.

Mungkasi, S. dan Supriyadi, B., 2016, Finite Volume Numerical Solvers For Non-Linear Elasticity In Heterogeneous Media, International Journal for Multiscale Computational Engineering, 14, 479.

(66)

Nilsson, S., Petersson, N.A., Sjögreen, B. dan Kreiss, H.O., 2007, Stable Difference Approximations For The Elastic Wave Equation In Second Order Formulation, SIAM Journal on Numerical Analysis, 45, 1902. Rachmayani, Dwi, 2014, Penerapan Pembelajaran Reciprocal Teaching untuk

Meningkatkan Kemampuan Komunikasi Matematis dan Kemandirian Belajar Matematika Siswa, Jurnal Pendidikan UNSIKA, 2, 1.

Schneider, M., Ospald, F. dan Kabel, M., 2016, Computational Homogenization Of Elasticity On A Staggered Grid, International Journal for Numerical Methods in Engineering, 105, 693.

Sjögreen, B. dan Petersson, N.A., 2012, A Fourth Order Accurate Finite Difference Scheme For The Elastic Wave Equation In Second Order Formulation, Journal of Scientific Computing, 52, 17.

Wazwaz, A.M., 2009, Partial differential Equations and Solitary Waves Theory, Springer, Berlin.

Yang, L., Yan, H. dan Liu, H., 2016, Optimal Implicit Staggered-Grid Finite-Difference Schemes Based On The Sampling Approximation Method For Seismic Modeling, Geophysical Prospecting, 64, 595.

Yang, L., Yan, H. dan Liu, H., 2017, An Optimal Implicit Staggered-Grid Finite-Difference Scheme Based On The Modified Taylor-Series Expansion With Minimax Approximation Method For Elastic Modeling, Journal of Applied Geophysics, 138, 161.

Yan, H-Y. dan Liu, Y., 2012, High-Order Finite-Difference Numerical Modeling Of Wave Propagation In Viscoelastic TTI Media Using Rotated Staggered Grid, Chinese Journal of Geophysics, 55, 252.

(67)

51

(68)

A. Program Matlab

clear all clc

N = 1000;%Number of cells

L = 10; %the length of the domain

dx=2*L/(N-1); %delta x

dt=0.05*dx; %delta t

tFinal = 5; % time of simulation

Nt = tFinal/dt; % banyaknya titik waktu

x = -10:dx:10; %interval x xodd = zeros(1, N/2); uodd = xodd; xeven = zeros(1, N/2); peven = xeven; p0=zeros(1,N); p=zeros(1,N); u0=zeros(1,N);

u=zeros(1,N); % storage of quantity % nilai awal

% for j=1:N; %iterasi j sebanyak 1 sampai N, dmna N merupakan banyaknya x % if x(j)<0 % p(j)=10; % else % p(j)=5; % end % end %initial condition for i=1:N

if x(i)<pi && x(i)>-pi

p(i) = 1 - cos(x(i)+pi); % u(x,0)

end end for i = 1:N if mod(i,2) == 0 xeven(i/2) = x(i); peven(i/2) = p(i); else xodd((i+1)/2) = x(i); uodd((i+1)/2) = u(i); end end

(69)

%perintah dibawah ini(47-55)dipakai untuk menggambar tekanan dan kecepatan saat %t=0 %plot(x,p) %xlabel('x') %ylabel('p') %plot(x,u) %xlabel('x') %ylabel('u') %stop for n=1:Nt p0 = p; u0 = u; for i = 2:N-1 if mod(i,2) == 0 %h grids

p(i) = p0(i) - dt/(2*dx)*(u0(i+1) - u0(i-1)); end end p(1) = 0; p(end) = 0; for i = 2:N-1 if mod(i,2)~= 0 %u-grids;

u(i) = u0(i) - dt/(2*dx)*(p0(i+1) - p0(i-1)); end end u(1) = 0; u(end) = 0; % pemilahan hasil for i = 1:N if mod(i,2) == 0 peven(i/2) = p(i); else uodd((i+1)/2) = u(i); end end

%plot the results

figure(1) subplot(2,1,1)

(70)

plot(xeven,peven) xlabel('x') ylabel('p(x,t)') subplot(2,1,2) plot(xodd,uodd) xlabel('x') ylabel('u(x,t)') pause(10^-10) t=n*dt; end

(71)

(72)