MODUL. STATA: LPM, LOGIT, dan PROBIT MODEL (Edisi:2011)

(1)

DEPARTEMEN ILMU EKONOMI

FAKULTAS EKONOMI UNIVERSITAS INDONESIA

MODUL

STATA: LPM, LOGIT, dan

PROBIT MODEL

(Edisi:2011)

Oleh :

Akbar Suwardi

Lab. Komputasi Departemen Ilmu Ekonomi

Gedung Departemen Ilmu Ekonomi-FEUI Lt. 1, Depok

Telp. (021) 78886252

(2)

LPM, Logit, dan Probit Model

PENGANTAR TEORI

Model dengan variabel dependen yang bersifat diskrit, maka estimasi dengan menggunakan regresi liner akan terasa dipaksakan, karena estimator yang

dihasilkan tidak lagi bersifat BLUE (Best Linier Unbiased Estimator). Hal ini

disebabkan: varian error-nya tidak terdistribusi normal, estimator tidak efisien akibat heteroskedastis, dan R² tidak dapat digunakan sebagai pengukur Goodness of

Fit. Oleh karenanya, untuk menghasilkan estimator persamaan yang BLUE,

penelitian ini menggunakan qualitative response regression model.

Terdapat tiga pendekatan untuk mengembangkan model yang menjelaskan model regresi binary response yaitu:

a. Linear Probability Model (LPM) b. Logit Model

c. Probit Model (Normit Model)

I. Linear Probability Model (LPM)

Linear Probability Model (LPM) merupakan metode regresi yang umum digunakan sebelum logit dan probit model dikembangkan. LPM bekerja dengan dasar bahwa variabel respon Y, yang merupakan probabilita terjadinya sesuatu, mengikuti

Bernoulli probability distribution dimana:

Yi Probability

1 1-Pi

0 Pi

(3)

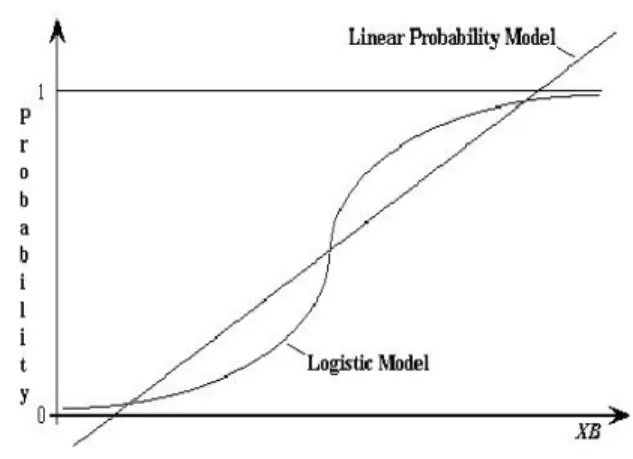
Sumber: wcr.sonoma.edu

Gambar diatas menunjukkan bahwa garis dari Linear Probability Model (LPM) sangat minim menjelaskan atau mempresentasikan dari variabel dependent yang diskrit. Oleh karena itu, karena LPM bekerja berdasarkan metode OLS biasa maka

timbul permasalahan yang telah diungkapkan sebelumnya: non-normality of the

disturbance, heteroscedastis, tidak terpenuhinya ekspektasi nilai Y antara satu sampai

dengan nol, dan tidak dapat digunakannya R² sebagai pengukur Goodness of Fit.

Kebutuhan akan model probabilita yang menghasilkan Y yang terletak antara interval satu sampai dengan nol dengan hubungan antara Pt dengan Xt yang tidak linear menyebabkan logit model dikembangkan.

II. LOGIT MODEL

Model Linear Probability Model memiliki masalah, tidak dapatnya memberikan hasil nilai Y yang terletak pada interval 1 dan 0, padahal niai probabilitas mengharuskan kisaran nilainya diantara 1 dan 0. dikarenakan mereka menggunakan OLS atau regresi linear dalam melakukan estimasinya, atau dengan persamaan sebagai berikut:

(4)

Dikarenakan persamaan regresi linear tidak dapat memenuhi persyaratan nilai probabilitas tersebut, di buatlah model logit yang menggunakan persamaan eksponensial untuk mendapatkan nilai probabilitas pada interval 1 dan 0, Dimana persamaan model Logit menjadi seperti berikut:

𝐏𝐏𝐏𝐏(𝒙𝒙) =_𝟏𝟏₊𝟏𝟏_𝐞𝐞_−𝐳𝐳= 𝟏𝟏

𝟏𝟏+𝐞𝐞−(𝛂𝛂+𝛃𝛃𝐱𝐱𝟏𝟏+𝛆𝛆)

Lalu persamaan tersebut disederhanakan menjadi:

Pi = i Z e− + 1 1 = _Z Z e e + 1 Dimana Zi = β1 + β2Xi.

Persamaan diatas lebih dikenal sebagai logistic distribution function. Persyaratan yang diminta sebelumnya, yaitu model probabilita yang menghasilkan Y antara interval satu sampai dengan nol dengan hubungan antara Pt dengan Xt yang tidak linear, dapat terpenuhi. Hal ini disebabkan, saat Z berkisar antara -∞ sampai dengan ∞, Pi

berkisar antara 0 dan 1 sehingga Pi tidak berhubungan linear dengan Z. Meskipun begitu masih terdapat masalah estimasi karena P tidak hanya tidak linier pada X

tetapi juga ke β. Namun, seperti dapat ditunjukkan pada persamaan berikut,

masalah estimasi tersebut dapat diatasi.

Setelah itu kita perlu menentukan persamaan kejadian gagal, dengan merujuk kepada Bernoulli probability distribution. Maka kita akan mendapatkan persamaan seperti dibawah ini:

(5)

Setelah kita memiliki persamaan kejadian sukses dan persamaan kejadian gagal,

maka kita dapat pula membuat Odds Ratio yang merupakan peluang sukses dibagi

dengan peluang gagal, dengan rumus matematika seperti dibawah.

𝐏𝐏𝐏𝐏(𝒙𝒙) 𝟏𝟏 − 𝐏𝐏𝐏𝐏(𝒙𝒙) = 𝐞𝐞𝐳𝐳 𝐞𝐞𝐳𝐳₊_𝟏𝟏 𝟏𝟏 𝟏𝟏+𝐞𝐞𝐳𝐳 = 𝐞𝐞𝐳𝐳

Untuk mendapatkan nilai z yang sudah linier maka kita perlu melakukan treatment tambahan setelah melakukan odd ratio dimana dengan mengalikan persamaan

diatas dengan Logaritma Natural dengan tujuan membuat persamaan menjadi

linear, sehingga bentuk persamaan akan menjadi seperti dibawah ini:

l𝐧𝐧 �_𝟏𝟏 ₋𝐏𝐏𝐏𝐏(_{𝐏𝐏𝐏𝐏}𝒙𝒙)₍_𝒙𝒙₎�=𝐳𝐳= 𝛂𝛂+𝛃𝛃𝐱𝐱𝟏𝟏+𝛆𝛆

Logaritma Natural atau ln dari odds ratio tidak hanya bersifat linear pada X tetapi juga bersifat linear terhadap parameter. Persamaan tersebut yang kemudian dikenal sebagai model logit. Kelebihan dari model logit tersebut adalah:

• Saat P berpindah dari 0 ke 1, logit L akan berpindah dari -∞ ke ∞.Oleh karena

itu, meskipun probabilita terletak antara 0 hingga 1, logit sendiri tidak terbatasi. Dan meski L linear terhadap X, probabilitanya sendiri tidak.

• L (logit) yang bernilai positif menandakan bahwa meningkatnya nilai

regresor akan menyebabkan meningkatnya odds dari regresan yang setara dengan 1. Sebaliknya, L (logit) yang bernilai negative menandakan bahwa menurunnya odds dari regresan yang setara dengan 1akan menyebabkan meningkatnya nilai dari X.

• Model logit yang diberikan pada persamaan lima dapat diinterpretasikan

(6)

perubahan nilai X, sementara Intercept β1 merupakan nilai dari log-odds apabila nilai suatu slope nol. Logit model juga mengasumsikan bahwa log sebuah odds ratio berhubungan linier terhadap Xi atau nilai sebuah slope.

Sumber: www.graphpad.com

Pengolahan Logit

• Untuk menguji signifikansi suatu koefisien secara statistik, kita

menggunakan Z statistik (distribusi normal).

• Dalam binary regressand model, kita menggunakan pseudo R2_{, yang mirip}

dengan R2_{, untuk mengukur}_{goodness of fit}_{. Program Stata secara otomatis}

menyediakan pengukuran tersebut, yaitu McFadden R2_{, yang ditulis dengan}

Pseudo R2.

• Mirip dengan F test pada model regresi linear adalah likelihood ratio (LR) statistik. LR statistik mengikuti ditribusi χ2 _{dengan derajat kebebasan}_(degree

of freedom) sama dengan jumlah variabel bebas

• Mencari Odds Ratio dari setiap variabel independent

• Margina Effek dari setiap variabel independent

• Mencari probabilitas setiap variabel independent terhadap variabel

(7)

III. Probit Model (Normit Model)

Model probit adalah salah satu model dari cummulative distribution function (CDF), yaitu model statistik yang sering digunakan untuk data dengan distribusi binomial. Model ini digunakan untuk menganalisis model dengan variabel dependen yang

memiliki hasil binary—yaitu y = 1 untuk menandakan suksesnya sebuah kejadian,

dan y = 0 untuk menandakan gagalnya sebuah kejadian. Terdapat beberapa asumsi yang mengikuti model probit, pertama, kita berasumsi bahwa peluang kejadian sukses satu kejadian bergantung kepada latent variabel atau yang tidak dapat di observasi, dimana akan ditentukan oleh variabel penjelas.

Jika nilai dari variabel yang tidak terobservasi semakin besar, maka peluang kejadian sukses akan semakin besar. Kedua, kita berasumsi bahwa terdapat nilai kritikal dari variabel yang tidak teramati, seperti jika variabel yang tidak teramati melewati tingkat kritikalnya, maka kejadian akan sukses, atau sebaliknya. Nilai

kritikal tidak teramati sama dengan variabel yang tidak teramati tersebut, tapi kita berasumsi bahwa nilai kritikal tersebut terdistribusi secara normal, dengan niai mean dan varians yang sama, dan sangat dimungkinkan bahwa tidak hanya digunakan untuk estimasi parameter variabel penjelas, tapi juga mendapatkan informasi mengenai variabel yang tidak teramati tersebut.

Dengan asumsi normalitas, probabilitas dari nilai kritikal kurang dari atau sama dengan variabel yang tidak teramati dapat dihitung melalui cumulative distributio

function. Sebagai contoh, jika keputusan keluarga memiliki ruah sendiri tergantung

dengan nilai utility index Ii variabel yang tidak teramati. Sementara indeks utilitas

sendiri ditentukan oleh pendapatan keluarga xi

(8)

Jika nilai kritikal Ii* lebih rendah atau sama dengan indeks utiitas Ii, keluarga akan

memiliki rumah, atau sebaliknya. Probabilitas Ii* ≤ I i dapat dihitung dari

standardize normal CDF:

Pi= P (Y = 1| X) = P (Ii* ≤ Ii) = P (Zi≤ β1+ β2 Xi) = F (β1+ β2 Xi)

Dimana P (Y = 1| X) artinya probabilitas kejadian terjadi pada nilai X yang tetap

dan dimana Zi adalah variabel standar normal. F adalah standar normal CDF.

Model matematis Probit sebagai berikut:

2_{/ 2}

1 ( )

2

i I z i

F I

e

dz

π

− −∞

=

∫

1 2 2_{/ 2}

1 ( )

2

i X z i

F I

β β

e

dz

π

+ ₋ −∞

=

∫

P adalah peluang kejadian sukses, maka nilai standar normal adalah diantara -∞ dan Ii, Indeks utilitas, sama seperti persamaan (β1 dan β2), kita melakukan inverse dari

CDF normal.

Ii = F-1 (Ii) = F-1 (Pi)

= β1+ β2 Xi

Dari persamaan diatas kita dapat mengestimasi parameter variabel penjelas dan variabel yang tidak teramati.

Pengolahan Probit

• Untuk menguji signifikansi suatu koefisien secara statistik, kita

menggunakan Z statistik (distribusi normal).

• Dalam binary regressand model, kita menggunakan pseudo R2_{, yang mirip}

(9)

menyediakan pengukuran tersebut, yaitu McFadden R2_{, yang ditulis dengan}

Pseudo R2.

• Mirip dengan F test pada model regresi linear adalah likelihood ratio (LR) statistik. LR statistik mengikuti ditribusi χ2 _{dengan derajat kebebasan}_(degree

of freedom) sama dengan jumlah variabel bebas

• Margina Effek dari setiap variabel independent

• Mencari probabilitas setiap variabel independent terhadap variabel

dependentnya

• Sensitivity; yang menyatakan seberapa besar hasil observasi positif secara

tepat dinyatakan positif.

• Specitivity; yang menyatakan seberapa besar hasil observasi negatif secara

tepat dinyatakan negatif.

• Meninjau grafik antar sensitivity/specitivity dan probability cut-off; jika koordinat (x < 0,5, y > 0,5) maka dapat dinyatakan bahwa model tersebut semakin baik dan stabil.

Sumber: teaching.sociology.ul.ie

Pada dasarnya perbedaan logit dan probit adalah Jika Logit – Cumulative standard

logistic distribution (F), sedangkan Probit – Cumulative standard normal

distribution (Φ). Namun Pada akhirnya dari dua model tersebut memiliki hasil yang persis sama.(Oscar Torres, P

rinceton University

)

(10)

APLIKASI PADA STATA

Pada contoh aplikasi ini yang kita gunakan adalah data mroz.dta, untuk mengetahui data kita tersebut seperti apa maka kita perlu mengenal data itu tersebut.

• Mengenal data

o Untuk mengetahui jenis data, variabel name, value label, format serta

varabel label kita dapat melakukannya sebagai berikut:

describe

Contains data from D:\Kelas Ekonomet2\lab1- Logit n Probit\mroz.dta obs: 753

vars: 22 2 Sep 1996 16:04 size: 39,909 (99.6% of memory free)

--- storage display value

variable name type format label variable label

--- inlf byte %9.0g =1 if in lab frce, 1975

hours int %9.0g hours worked, 1975 kidslt6 byte %9.0g # kids < 6 years kidsge6 byte %9.0g # kids 6-18

age byte %9.0g woman's age in yrs educ byte %9.0g years of schooling wage float %9.0g est. wage from earn, hrs repwage float %9.0g rep. wage at interview in 1976 hushrs int %9.0g hours worked by husband, 1975 husage byte %9.0g husband's age

huseduc byte %9.0g husband's years of schooling huswage float %9.0g husband's hourly wage, 1975 faminc float %9.0g family income, 1975

mtr float %9.0g fed. marg. tax rte facing woman motheduc byte %9.0g mother's years of schooling fatheduc byte %9.0g father's years of schooling unem float %9.0g unem. rate in county of resid. city byte %9.0g =1 if live in SMSA

exper byte %9.0g actual labor mkt exper nwifeinc float %9.0g (faminc - wage*hours)/1000 lwage float %9.0g log(wage)

expersq int %9.0g exper^2

(11)

o Untuk mengetahui berapa jumlah observasi, mean, std.deviasi,

nilai max dan nilai minimum kita dapat melakukannya sebagai berikut:

sum

o Untuk mengetahui suatu komposisi nilai dari suatu nilai

dummy, kita dapat melakukannya sebagai berikut: (misal variabel yang kita ingin tahu adalah inlf)

(12)

o Untuk membuat lebih mudah dalam simulasi model logit dan

probit didalam modul ini, kita akan membuat variabel baru yaitu variabel individu awal. Dengan cara:

gen idawal = _n

• Model yang digunakan

Setelah kita mengetahui jenis data kita serta mengetahui berapa jumlah observasi, mean, std.deviasi, nilai max dan nilai minimum, maka kita masuk kedalam model yang ingin kita gunakan. Contoh model pada modul untuk data ini adalah

ε

β

α

kidsge6 kidslt6 age educ nwifeinc exper ) 1 infl ( = = + 1 + 2 + 3 + 4 + 5 + 6 + P Keterangan:

inlf adalah =1 if in lab force in 1975,

kidsge6 adalah number of kids aged 6-18

kidslt6 adalah number of kids aged < 6 years

age adalah woman's age in years

educ adalah years of schooling

nwifeinc adalah (faminc - wage*hours)/1000

(13)

1. LPM

reg inlf kidslt6 kidsge6 age educ nwifeinc exper

Source | SS df MS Number of obs = 753 ---+--- F( 6, 746) = 42.32 Model | 46.9082358 6 7.8180393 Prob > F = 0.0000 Residual | 137.81952 746 .184744665 R-squared = 0.2539 ---+--- Adj R-squared = 0.2479 Total | 184.727756 752 .245648611 Root MSE = .42982

Karena kita melakukan data menggunakan LPM dimana berdasarkan OLS, maka dari hasil diatas kita dapat membuat model menjadi seperti berikut: (yaitu dengan memasukan koefisient ke model awal)

exper 0.023 nwifeinc 003 . 0 educ 039 . 0 age 017 . 0 kidsge6 013 . 0 kidslt6 271 . 0 707 . 0 ) 1 infl ( = = − + − + − + P

• Melihat nilai prediksi dan error dari estimasi menggunakan LPM

reg inlf kidslt6 kidsge6 age educ nwifeinc exper (omitted)

predict lpminlfhat  (untuk mendapatkan nilai inlf estimasi)

predict erlpm, resid  (untuk mendapatkan nilai error dari inlf

estimasi (lpminlfhat))

(14)

+---+ | inlf lpminl~t erlpm | |---| 26. | 1 1.030639 -.030639 | 27. | 1 .7865728 .2134272 | 28. | 1 .8024666 .1975335 | 29. | 1 .6710289 .3289711 | 30. | 1 .5469357 .4530643 | |---| 31. | 1 .9649304 .0350696 | 32. | 1 .4919043 .5080957 | 33. | 1 .9282249 .0717751 | 34. | 1 .5534077 .4465922 | 35. | 1 1.138675 -.1386752 | +---+

list inlf lpminlfhat erlpm in 481/485

+---+ | inlf lpminl~t perlpm | |---| 481. | 0 .4951564 -.4951564 | 482. | 0 .5932751 -.5932751 | 483. | 0 .065651 -.065651 | 484. | 0 -.3042662 .3042662 | 485. | 0 .0083976 -.0083976 | +---+

Contoh, jika kita punya data pada list 26, dengan nilai setiap variabel, dapat dilihat dengan cara berikut:

List inlf kidslt6 kidsge6 age educ nwifeinc exper lpminlfhat erlpm in 26

+---+ | inlf kidslt6 kidsge6 age educ nwifeinc exper lpminl~t erlpm | |---| 26. | 1 0 2 43 17 27.34999 21 1.030639 -.030639 | +---+

Nilai Prediksi dengan LPM Nilai Prediksi dengan

(15)

Dimana dari nilai variabel tersebut kita masukin kedalam model LPM yang telah kita dapatkan koefisienya dari hasil estimasi di atas. Terlihat bahwa estimasi yang kita peroleh bisa lebih dari 1, padahal data sebenarnya data kita hanya antara 0 dan 1. Oleh karena itu, permasalahan tersebut merupakan salah satu kelemahan dari LPM.

• Grafik scatterplot

Untuk memperjelas hasil dari estimasi menggunakan LPM (lpminlfhat) maka nilainya dapat kita gambarkan menggunakan scatter plot, dengan cara seperti berikut:

1. Membuat Scatter Plot berdasarkan FittedValues

scatter inlf lpminlfhat || lfit inlf lpminlfhat

2. Membuat Scatter Plot berdasarkan nilai Estimasi menggunakan LPM

sort lpminlfhat gen idlpmm = _n

scatter lpminlfhat inlf idlpmm

-. 5 0 .5 1 1. 5 -.5 0 .5 1 1.5 Fitted values

(16)

Dari hasil kedua scatter plot diatas menunjukkan bahwa nilai FittedValues

dan estimasi menggunakan LPM (lpminlfhat) keluar dari nilai inlf

aslinya, yaitu antara 0 dan 1.

3. Membuat Scatter Plot nilai predicted (yˆ) berdasarkan nilai residual (uˆ)

dari nilai Estimasi menggunakan LPM akan terlihat seperti berikut: rvfplot

Karena uˆ= y−yˆ, maka uˆ=−yˆ ketika y=0  (the lower line in the above graph yaitu -1), sedangkan uˆ=1−yˆ ketika y=1  (the upper line). -. 5 0 .5 1 1. 5 0 200 400 600 800 idlpmm

Fitted values =1 if in lab frce, 1975

-1 -.5 0 .5 1 Re si d ua ls -.5 0 .5 1 Fitted values

(17)

2. LOGIT

logit inlf kidslt6 kidsge6 age educ nwifeinc exper

Iteration 0: log likelihood = -514.8732 Iteration 1: log likelihood = -406.91038 Iteration 2: log likelihood = -406.14404 Iteration 3: log likelihood = -406.14318 Iteration 4: log likelihood = -406.14318

Logistic regression Number of obs = 753 LR chi2(6) = 217.46 Prob > chi2 = 0.0000 Log likelihood = -406.14318 Pseudo R2 = 0.2112

Dari hasil regress kita menggunakan logit maka kita mendapatkan koefisient untuk dimasukan kedalam rumus logistik,

Pi = i Z e− + 1 1 = _Z Z e e + 1

menjadi seperti berikut:

𝐏𝐏𝐏𝐏

(

𝒊𝒊𝒊𝒊𝒊𝒊𝒊𝒊

=

𝟏𝟏 )

=

_𝐞𝐞

_𝟎𝟎

𝐞𝐞

_._{𝟖𝟖𝟖𝟖𝟖𝟖−𝟏𝟏}𝟎𝟎.𝟖𝟖𝟖𝟖𝟖𝟖−𝟏𝟏_._{𝟒𝟒𝟖𝟖𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒}.𝟒𝟒𝟖𝟖𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒₊_𝟎𝟎+_._{𝟎𝟎𝟎𝟎𝟖𝟖𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟎𝟎𝐞𝐞𝟒𝟒−𝟎𝟎}𝟎𝟎.𝟎𝟎𝟎𝟎𝟖𝟖𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟎𝟎𝐞𝐞𝟒𝟒−𝟎𝟎_._{𝟎𝟎𝟒𝟒𝟏𝟏𝟎𝟎𝟎𝟎𝐞𝐞}.𝟎𝟎𝟒𝟒𝟏𝟏𝟎𝟎𝟎𝟎𝐞𝐞₊_𝟎𝟎+_._{𝟐𝟐𝟐𝟐𝟖𝟖𝐞𝐞𝟒𝟒𝟐𝟐𝐜𝐜−𝟎𝟎}𝟎𝟎.𝟐𝟐𝟐𝟐𝟖𝟖𝐞𝐞𝟒𝟒𝟐𝟐𝐜𝐜−𝟎𝟎_._{𝟎𝟎𝟐𝟐𝟎𝟎𝐧𝐧𝟎𝟎𝟒𝟒𝟎𝟎𝐞𝐞𝟒𝟒𝐧𝐧𝐜𝐜}.𝟎𝟎𝟐𝟐𝟎𝟎𝐧𝐧𝟎𝟎𝟒𝟒𝟎𝟎𝐞𝐞𝟒𝟒𝐧𝐧𝐜𝐜₊_𝟎𝟎+_._{𝟏𝟏𝟏𝟏𝟒𝟒𝐞𝐞𝐱𝐱𝟏𝟏𝐞𝐞}𝟎𝟎.𝟏𝟏𝟏𝟏𝟒𝟒𝐞𝐞𝐱𝐱𝟏𝟏𝐞𝐞𝐏𝐏

₊

_𝟏𝟏

Contoh, misalkan kita ingin melihat data kita pada baris satu dari stata dan melihat berapa nilai probabilitas prediksi dengan logit, maka dapat dilakukan dengan seperti berikut:

(18)

logit inlf kidslt6 kidsge6 age educ nwifeinc exper

predict plgtinlfht  (untuk mendapatkan nilai probabilitas inlf estimasi)

Sebelum kita ingin melihat nilai dari list, kita harus membuat urutan dalam data seperti semua, dengan cara:

sort idawal

list inlf kidslt6 kidsge6 age educ nwifeinc exper plgtinlfht in 1

+---+

| inlf kidslt6 kidsge6 age educ nwifeinc exper plgiti~t| |---| 1. | 1 1 0 32 12 10.91006 14 .6599977 | +---+

Dengan memasukan rumus yang telah memiliki keofisien kita akan mendapatkan nilai inlf estimasi (plgtinlfht), atau nilai Probabilitas prediksi dengan rumus seperti ini:

𝐏𝐏𝐏𝐏

(

𝒊𝒊𝒊𝒊𝒊𝒊𝒊𝒊

=

𝟏𝟏 )

=

_𝐞𝐞

_𝟎𝟎

𝐞𝐞

_._{𝟖𝟖𝟖𝟖𝟖𝟖−𝟏𝟏}𝟎𝟎.𝟖𝟖𝟖𝟖𝟖𝟖−𝟏𝟏_._{𝟒𝟒𝟖𝟖𝟒𝟒}.𝟒𝟒𝟖𝟖𝟒𝟒₍_𝟏𝟏₎₊(𝟏𝟏_𝟎𝟎)+_._{𝟎𝟎𝟎𝟎𝟖𝟖}𝟎𝟎.𝟎𝟎𝟎𝟎𝟖𝟖₍_𝟎𝟎₎(_−𝟎𝟎𝟎𝟎)−𝟎𝟎_._{𝟎𝟎𝟒𝟒𝟏𝟏}.𝟎𝟎𝟒𝟒𝟏𝟏₍_{𝟖𝟖𝟐𝟐}(₎₊𝟖𝟖𝟐𝟐_𝟎𝟎)+_._{𝟐𝟐𝟐𝟐𝟖𝟖}𝟎𝟎.𝟐𝟐𝟐𝟐𝟖𝟖₍_{𝟏𝟏𝟐𝟐}(𝟏𝟏𝟐𝟐₎_−𝟎𝟎)−𝟎𝟎_._{𝟎𝟎𝟐𝟐𝟎𝟎}.𝟎𝟎𝟐𝟐𝟎𝟎₍_{𝟏𝟏𝟎𝟎}(_.𝟏𝟏𝟎𝟎_{𝟒𝟒𝟏𝟏}.₎₊𝟒𝟒𝟏𝟏_𝟎𝟎)+_._{𝟏𝟏𝟏𝟏𝟒𝟒}𝟎𝟎.𝟏𝟏𝟏𝟏𝟒𝟒₍_{𝟏𝟏𝟒𝟒}(₎𝟏𝟏𝟒𝟒

₊

)

_𝟏𝟏

=

𝟎𝟎 .

𝟒𝟒𝟎𝟎𝟒𝟒𝟒𝟒𝟒𝟒𝟖𝟖𝟖𝟖

Nilai Probabilitas inlf=1 dengan Logit

(19)

• Lihat odds ratio

logit inlf kidslt6 kidsge6 age educ nwifeinc exper, or

Logistic regression Number of obs = 753 LR chi2(6) = 217.46 Prob > chi2 = 0.0000 Log likelihood = -406.14318 Pseudo R2 = 0.2112

• Melihat Odds ratio pada different levels di setiap variable

logit inlf kidslt6 kidsge6 age educ nwifeinc exper (omitted)

adjust, by (kidslt6) exp

--- Dependent variable: inlf Equation: inlf Command: logit

Variables left as is: kidsge6, age, educ, exper, nwifeinc

---

--- # kids < |

Nilai Odds Ratio mewakili kemungkinan untuk inlf = 1 ketika variabel meningkat sebesar 1 unit. Nilai ini adalah exp (logit coeff). Jika > ATAU 1 maka kemungkinan inlf = 1 meningkat. Jika < ATAU 1 maka kemungkinan inlf = 1 menurun. Lihatlah tanda koefisien logit

(20)

6 years | exp(xb) ---+--- 0 | 1.85037 1 | .589443 2 | .289553 3 | .023302 ---

Key: exp(xb) = exp(xb)

Penjelasannya: ketika kids<6 years = 0 (perempuan tidak memiliki anak dibawah 6 tahun) maka kemungkinan (the odds of) inlf=1 (bekerja) akan meningkat dengan faktor sebesar 1.85037 (controlling by the other variables). Misalnya contoh lain, ketika kids<6 years = 3 (perempuan memiliki anak dibawah 6 tahun sebanyak 3)

maka kemungkinan (the odds of) inlf=1 (bekerja) hours akan meningkat dengan

faktor sebesar .023302 (controlling by the other variables).

• Memprediksi probabilitas pada different levels di setiap variable di Model

Logit

adjust, by (kidslt6) pr

--- Dependent variable: inlf Equation: inlf Command: logit

--- --- # kids < | 6 years | pr ---+--- 0 | .649168 1 | .370849 2 | .224538

(21)

3 | .022772 ---

Key: pr = Probability

Penjelasannya: ketika kids<6 years = 0 (perempuan tidak memiliki anak dibawah 6 tahun) maka probabilita inlf=1 (kerja) adalah .649168 atau 64.91%. (controlling by the other variables). ketika kids<6 years = 2 (perempuan memiliki anak dibawah 6

tahun sebanyak 2) maka probabilita inlf=1 (kerja) adalah .224538 atau 22.45%.

(controlling by the other variables). Hasil dari Probabilitas tersebut berasal dari persamaan logit diatas.

• Efek marginal rata-rata dari setiap variabel peubah (multiplier) Model

Logit

Mfx

Marginal effects after logit y = Pr(inlf) (predict) = .58774394

Penjelasannya: Pertama, terlihat bahwa ada marjinal efek tabel terpisah untuk setiap alternatif dan tabel yang diawali dengan melaporkan keseluruhan probabilitas memilih alternatif, misalnya, 0,58774394. Kedua, penjelasan untuk marginal tiap variable, misal untuk variabel kidslt6, secara rata-rata ketika nilai kidslt6 naik satu

Nilai yang berada di kolom X adalah nilai rata-rata dari setiap variabel (lihat sum per variabel)

(22)

satuan maka kemungkinan perempuan untuk infl=1 (bekerja) akan turun sebesar 0.3487663 point atau 34.88%. contoh lain, misal untuk variabel educ, secara rata-rata

ketika nilai educ naik satu satuan maka kemungkinan perempuan untuk infl=1

(bekerja) akan naik sebesar 0.0549967 point atau sebesar 5.5%.

• Pengujian Goodness of Fit

Pengujian ini perlu dilakukan karena hasil Pseudo R2 hasil dari persamaan

diragukan untuk di analisa, karena hasil yang cukup lemah. Untuk itu kita perlu

mencari R2 lain misalnya dengan McFadden’s R2, Efron’s R2 dll. Selain itu

pengujian ini menampilkan nilai aic & bic, hasil ini bisa kita bandingkan dengan persamaan lain yang kita buat, semakin keci aic & bic semakin baik. Pengujian

Goodness of Fit dapat dilakukan dengan cara,

logit inlf kidslt6 kidsge6 age educ nwifeinc exper (Omitted)

fitstat

(Jika perintah fitstat dijalankan, hasil yang keluar “unrecognized command:

fitstat” maka anda perlu untuk mengUpdate perintah. Dengan cara keitik

“help fitstat”, setelah itu klik tulisan sg145 lalu ikuti perintah untuk meng install)

Measures of Fit for logit of inlf

Log-Lik Intercept Only: -514.873 Log-Lik Full Model: -406.143 D(746): 812.286 LR(6): 217.460 Prob > LR: 0.000 McFadden's R2: 0.211 McFadden's Adj R2: 0.198 Maximum Likelihood R2: 0.251 Cragg & Uhler's R2: 0.337 McKelvey and Zavoina's R2: 0.354 Efron's R2: 0.261 Variance of y*: 5.090 Variance of error: 3.290 Count R2: 0.742 Adj Count R2: 0.403 AIC: 1.097 AIC*n: 826.286 BIC: -4129.266 BIC': -177.716

(23)

Hasil diatas menyatakan bahwa McFadden's Adj R2 = 0.198, yang dapat diartikan sebagai berikut garis regresi mampu menjelaskan variasi penyebaran dependen dengan menggunakan kurva sigmoid sebesar 19.8% yang lebih kecil dari nilai

McFadden's R2 = 0.211 atau sebagai berikut garis regresi mampu menjelaskan

variasi penyebaran dependen dengan menggunakan kurva sigmoid sebesar 21.1%.

• Pengujian Goodness of Fit Hosmer-Lemeshow

Pengujian Hosmer-Lemeshow (2000) menyajikan Pearson X2_{goodness-of-fit test}

untuk the fitted model atau pengujian ini mirip dengan uji global pada OLS. Pengujian Pearson X2_{goodness-of-fit adalah sebuah test terhadap hasil data yang}

observed terhadap expected number of responses dimana menggunakan covariate

patterns (Manual Stata11). Pengujian Hosmer-Lemeshow dapat dilakukan dengan

cara seperti berikut:

estat gof

Logistic model for inlf, goodness-of-fit test

number of observations = 753 number of covariate patterns = 753 Pearson chi2(746) = 753.63 Prob > chi2 = 0.4152

Pada hasil model kita, model fits hasilnya sangat baik. Dimana, nilai number of

covariate patterns saama dengan number of observations yaitu 753, sedangkan nilai dari

(Prob>chi2) lebih besar dari α atau terima H0. Dimana memilki hipotesisi seperti berikut:

(24)

H1 : 𝑦𝑦 ≠ 𝑦𝑦� ∶ Tolak Model

• Pengujian Sensitivity dan Specitivity

Pada pengujian ini prinsipnya sama dengan uji goodness of fit sebagai bentuk

perwakilan pengganti R2, dengan melihat melalui specitivity & sensitivity. Dengan cara:

estat classification

Logistic model for inlf

--- True --- Classified | D ~D | Total ---+---+--- + | 347 113 | 460 - | 81 212 | 293 ---+---+--- Total | 428 325 | 753 Classified + if predicted Pr(D) >= .5 True D defined as inlf != 0

Berdasarkan hasil diatas dapat disimpulkan:

o Specitivity : observasi hasil negative yang dinyatakan secara negative

secara benar sebesar 65.23%%

o Sensitivity : observasi hasil positive yang dinyatakan secara positive

secara benar sebesar 81.07%

o Secara Overall : model mampu menyatakan secara benar sebesar

(25)

Untuk memperjelas hasil dari estimasi menggunakan Logit (logitinlfhat) maka nilainya dapat kita gambarkan menggunakan scatter plot, dengan cara seperti berikut:

1. Membuat grafik Scatter Plot Transformasi logit

Kita harus membuat variable baru, yaitu berisi ln dari (probabilitas/(1-probabilitas)), seperti yang tertera dalam grafik dalam membuat kurva transformasi logit. Dengan cara:

gen lnplgtinlfht = ln( plgtinlfht/(1- plgtinlfht)) scatter plgtinlfht inlf lnplgtinlfht

2. Membuat Scatter Plot berdasarkan nilai Probabilitas Estimasi

menggunakan Logit, dengan cara:

sort plgtinlfht gen idlogit = _n

scatter plgtinlfht inlf idlogit

0 .2 .4 .6 .8 1 -4 -2 0 2 4 lnplgtinlfht Pr(inlf) =1 if in lab frce, 1975

(26)

Dari hasil kedua scatter plot diatas menunjukkan bahwa nilai Transformasi logit dan Probabilitas Estimasi menggunakan Logit (plgtinlfht) tidak keluar dari nilai inlf aslinya, yaitu antara 0 dan 1. Berbeda dengan hasil dari LPM.

0 .2 .4 .6 .8 1 0 200 400 600 800 idlogit

(27)

3. PROBIT

probit inlf kidslt6 kidsge6 age educ nwifeinc exper

Probit regression Number of obs = 753 LR chi2(6) = 217.31 Prob > chi2 = 0.0000 Log likelihood = -406.21886 Pseudo R2 = 0.2110

Dari hasil regress kita menggunakan Probit maka kita mendapatkan koefisient untuk dimasukan kedalam rumus Probabiltas (probit) berikut: menjadi seperti berikut: 𝑭𝑭 (𝑰𝑰𝒊𝒊) = 𝟏𝟏 √𝟐𝟐𝟐𝟐� 𝒆𝒆−𝒛𝒛 𝟐𝟐_/_𝟐𝟐 𝑰𝑰𝒊𝒊 −∞ 𝒅𝒅𝒛𝒛 𝑭𝑭 (𝑰𝑰𝒊𝒊) = 𝟏𝟏 √𝟐𝟐𝟐𝟐� 𝒆𝒆−𝒛𝒛 𝟐𝟐_/_𝟐𝟐 𝜷𝜷𝟏𝟏+𝜷𝜷𝟐𝟐𝑿𝑿𝒊𝒊 −∞ 𝒅𝒅𝒛𝒛 Pi= P (Y = 1| X) = P (Ii* ≤ Ii) = P (Zi≤ β1+ β2 Xi) = F (β1+ β2 Xi) menjadi seperti berikut:

𝑭𝑭

(

𝑰𝑰

𝒊𝒊

) =

𝟏𝟏 √𝟐𝟐𝟐𝟐

�

𝒆𝒆

−𝒛𝒛

𝟐𝟐_/_𝟐𝟐

(𝟎𝟎.𝟎𝟎𝟖𝟖𝟒𝟒−𝟎𝟎.𝟖𝟖𝟖𝟖𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒+𝟎𝟎.𝟎𝟎𝟖𝟖𝟎𝟎𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟎𝟎𝐞𝐞𝟒𝟒−𝟎𝟎.𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝐞𝐞+𝟎𝟎.𝟏𝟏𝟖𝟖𝟖𝟖𝐞𝐞𝟒𝟒𝟐𝟐𝐜𝐜−𝟎𝟎.𝟎𝟎𝟏𝟏𝟏𝟏𝐧𝐧𝟎𝟎𝟒𝟒𝟎𝟎𝐞𝐞𝟒𝟒𝐧𝐧𝐜𝐜+𝟎𝟎.𝟎𝟎𝟖𝟖𝟎𝟎𝐞𝐞𝐱𝐱𝟏𝟏𝐞𝐞𝐏𝐏 )

(28)

𝐏𝐏

𝟒𝟒

=

𝐅𝐅

(

𝛃𝛃𝟏𝟏

+

𝛃𝛃𝟐𝟐

𝐗𝐗𝟒𝟒

)

= 𝐅𝐅 (𝟎𝟎.𝟎𝟎𝟖𝟖𝟒𝟒 − 𝟎𝟎.𝟖𝟖𝟖𝟖𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒+𝟎𝟎.𝟎𝟎𝟖𝟖𝟎𝟎𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟎𝟎𝐞𝐞𝟒𝟒 − 𝟎𝟎.𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝐞𝐞+𝟎𝟎.𝟏𝟏𝟖𝟖𝟖𝟖𝐞𝐞𝟒𝟒𝟐𝟐𝐜𝐜 − 𝟎𝟎.𝟎𝟎𝟏𝟏𝟏𝟏𝐧𝐧𝟎𝟎𝟒𝟒𝟎𝟎𝐞𝐞𝟒𝟒𝐧𝐧𝐜𝐜 +𝟎𝟎.𝟎𝟎𝟖𝟖𝟎𝟎𝐞𝐞𝐱𝐱𝟏𝟏𝐞𝐞𝐏𝐏)

Contoh, misalkan kita ingin melihat data kita pada baris satu dari stata dan melihat

berapa Nilai Probabilitas Prediksi dengan probit, maka dapat dilakukan dengan

seperti berikut:

probit inlf kidslt6 kidsge6 age educ nwifeinc exper

predict prinlfhat  (untuk mendapatkan nilai probabilitas inlf estimasi)

Sebelum kita ingin melihat nilai dari list, kita harus membuat urutan dalam data seperti semua, dengan cara:

sort idawal

list inlf kidslt6 kidsge6 age educ nwifeinc exper prinlfhat in 1

+---+ | inlf kidslt6 kidsge6 age educ nwifeinc exper prinl~t | |---| 1. | 1 1 0 32 12 10.91006 14 .6512424 | +---+

Dengan memasukan nilai-nilai diatas kedalam rumus yang telah memiliki keofisien, kita akan mendapatkan nilai inlf estimasi (proinlfhat) atau nilai Probabilitas prediksi dengan proses seperti berikut :

Nilai Probabilitas inlf=1 dengan Probit

(29)

𝑭𝑭

(

𝑰𝑰

𝒊𝒊

) =

𝟏𝟏 √𝟐𝟐𝟐𝟐

�

𝒆𝒆

−𝒛𝒛𝟐𝟐_/_𝟐𝟐 (𝟎𝟎.𝟎𝟎𝟖𝟖𝟒𝟒−𝟎𝟎.𝟖𝟖𝟖𝟖𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒+𝟎𝟎.𝟎𝟎𝟖𝟖𝟎𝟎𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟒𝟎𝟎𝐞𝐞𝟒𝟒−𝟎𝟎.𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝐞𝐞+𝟎𝟎.𝟏𝟏𝟖𝟖𝟖𝟖𝐞𝐞𝟒𝟒𝟐𝟐𝐜𝐜−𝟎𝟎.𝟎𝟎𝟏𝟏𝟏𝟏𝐧𝐧𝟎𝟎𝟒𝟒𝟎𝟎𝐞𝐞𝟒𝟒𝐧𝐧𝐜𝐜+𝟎𝟎.𝟎𝟎𝟖𝟖𝟎𝟎𝐞𝐞𝐱𝐱𝟏𝟏𝐞𝐞𝐏𝐏 ) −∞

𝒅𝒅𝒛𝒛

𝐏𝐏

_𝟒𝟒

=

𝐅𝐅

(

𝛃𝛃𝟏𝟏

+

𝛃𝛃𝟐𝟐

𝐗𝐗𝟒𝟒

)

= 𝐅𝐅 (𝟎𝟎.𝟎𝟎𝟖𝟖𝟒𝟒 − 𝟎𝟎.𝟖𝟖𝟖𝟖𝟒𝟒(𝟏𝟏) +𝟎𝟎.𝟎𝟎𝟖𝟖𝟎𝟎(𝟎𝟎)− 𝟎𝟎.𝟎𝟎𝟎𝟎𝟎𝟎(𝟖𝟖𝟐𝟐) +𝟎𝟎.𝟏𝟏𝟖𝟖𝟖𝟖(𝟏𝟏𝟐𝟐) − 𝟎𝟎.𝟎𝟎𝟏𝟏𝟏𝟏(𝟏𝟏𝟎𝟎.𝟒𝟒𝟏𝟏𝟎𝟎𝟎𝟎𝟒𝟒) +𝟎𝟎.𝟎𝟎𝟖𝟖𝟎𝟎(𝟏𝟏𝟒𝟒) = 0.6512424

• Melihat exp (e) ratio pada different levels di setiap variable di Model

Probit

adjust, by (kidslt6) exp

--- Dependent variable: inlf Equation: inlf Command: probit

--- --- # kids < | 6 years | exp(xb) ---+--- 0 | 1.4445 1 | .730329 2 | .469383 3 | .104823 ---

Key: exp(xb) = exp(xb)

Penjelasannya: ketika kids<6 years = 0 (perempuan tidak memiliki anak dibawah 6 tahun) maka kemungkinan (the odds of) inlf=1 (bekerja) akan meningkat dengan

Nilai Probabilitas inlf=1 dengan Probit

(30)

faktor sebesar 1.4445 (controlling by the other variables). Misalnya contoh lain, ketika kids<6 years = 3 (perempuan memiliki anak dibawah 6 tahun sebanyak 3)

maka kemungkinan (the odds of) inlf=1 (bekerja) hours akan meningkat dengan

faktor sebesar 0.104823 (controlling by the other variables).

• Memprediksi probabilitas pada different levels di setiap variable di Model

Probit

adjust, by (kidslt6) pr

--- Dependent variable: inlf Equation: inlf Command: probit

--- --- # kids < | 6 years | pr ---+--- 0 | .643474 1 | .376662 2 | .224724 3 | .012051 --- Key: pr = Probability

Penjelasannya: ketika kids<6 years = 0 (perempuan tidak memiliki anak dibawah 6 tahun) maka probabilita inlf=1 (kerja) adalah 0.643474 atau 64.38 %. (controlling by the other variables). ketika kids<6 years = 2 (perempuan memiliki anak dibawah 6

tahun sebanyak 2) maka probabilita inlf=1 (kerja) adalah 0.224724 atau 22.47%.

(controlling by the other variables). Hasil dari Probabilitas tersebut berasal dari persamaan logit diatas.

(31)

• Efek marginal rata-rata dari setiap variabel perubah (multiplier)

probit inlf kidslt6 kidsge6 age educ nwifeinc exper (omitted)

mfx

Marginal effects after probit y = Pr(inlf) (predict) = .58379791

Penjelasannya: Pertama terlihat bahwa ada marjinal efek tabel terpisah untuk setiap alternatif dan tabel yang diawali dengan melaporkan keseluruhan probabilitas memilih alternatif, misalnya, 0.58379791. Sedangkan penjelasan untuk marginal tiap variable, misal untuk variabel kidslt6, secara rata-rata ketika nilai kidslt6 naik satu satuan maka kemungkinan perempuan untuk infl=1 (bekerja) akan turun sebesar 0.341069 point atau 34.11%. contoh lain, misal untuk variabel educ, secara rata-rata

ketika nilai educ naik satu satuan maka kemungkinan perempuan untuk infl=1

(bekerja) akan naik sebesar 0.0521537point atau sebesar 5.2%.

• Pengujian Goodness of Fit

Pengujian ini perlu dilakukan karena hasil Pseudo R2 hasil dari persamaan

diragukan untuk di analisa, karena hasil yang cukup lemah. Untuk itu kita perlu

mencari R2 lain misalnya dengan McFadden’s R2, Efron’s R2 dll. Selain itu

pengujian ini menampilkan nilai aic & bic, hasil ini bisa kita bandingkan dengan persamaan lain yang kita buat, semakin keci aic & bic semakin baik. Pengujian

Goodness of Fit dapat dilakukan dengan cara,

Nilai yang berada di kolom X adalah nilai rata-rata dari setiap variabel (lihat sum per variabel)

(32)

probit inlf kidslt6 kidsge6 age educ nwifeinc exper (Omitted)

fitstat

(Jika perintah fitstat dijalankan, hasil yang keluar “unrecognized command:

fitstat” maka anda perlu untuk mengUpdate perintah. Dengan cara keitik

“help fitstat”, setelah itu klik tulisan sg145

• Pengujian Goodness of Fit Hosmer-Lemeshow

lalu ikuti perintah untuk meng install)

Measures of Fit for probit of inlf

Log-Lik Intercept Only: -514.873 Log-Lik Full Model: -406.219 D(746): 812.438 LR(6): 217.309 Prob > LR: 0.000 McFadden's R2: 0.211 McFadden's Adj R2: 0.197 Maximum Likelihood R2: 0.251 Cragg & Uhler's R2: 0.336 McKelvey and Zavoina's R2: 0.388 Efron's R2: 0.261 Variance of y*: 1.633 Variance of error: 1.000 Count R2: 0.745 Adj Count R2: 0.409 AIC: 1.098 AIC*n: 826.438 BIC: -4129.115 BIC': -177.564

Hasil diatas menyatakan bahwa McFadden's Adj R2 = 0.198, yang dapat diartikan sebagai berikut garis regresi mampu menjelaskan variasi penyebaran dependen dengan menggunakan kurva sigmoid sebesar 19.7% yang lebih kecil dari nilai

McFadden's R2 = 0.211 atau sebagai berikut garis regresi mampu menjelaskan

variasi penyebaran dependen dengan menggunakan kurva sigmoid sebesar 21.1%.

Pengujian Hosmer-Lemeshow (2000) menyajikan Pearson X2_{goodness-of-fit test}

untuk the fitted model atau pengujian ini mirip dengan uji global pada OLS. Pengujian Pearson X2_{goodness-of-fit adalah sebuah test terhadap hasil data yang}

observed terhadap expected number of responses dimana menggunakan covariate

patterns (Manual Stata11). Pengujian Hosmer-Lemeshow dapat dilakukan dengan

(33)

estat gof

Probit model for inlf, goodness-of-fit test

number of observations = 753 number of covariate patterns = 753 Pearson chi2(746) = 758.31 Prob > chi2 = 0.3691

Pada hasil model kita, model fits hasilnya sangat baik. Dimana, nilai number of

covariate patterns saama dengan number of observations yaitu 753, sedangkan nilai dari

(Prob>chi2) lebih besar dari α atau terima H0. Dimana memilki hipotesis seperti berikut:

H0 : 𝑦𝑦 =𝑦𝑦� ∶ Tidak Tolak Model

H1 : 𝑦𝑦 ≠ 𝑦𝑦� ∶ Tolak Model

• Pengujian Sensitivity dan Specitivity

Pada pengujian ini prinsipnya sama dengan uji goodness of fit sebagai bentuk

perwakilan pengganti R2, dengan melihat melalui specitivity & sensitivity. Dengan cara:

estat classification

Probit model for inlf

--- True --- Classified | D ~D | Total ---+---+--- + | 348 112 | 460 - | 80 213 | 293 ---+---+--- Total | 428 325 | 753

(34)

Classified + if predicted Pr(D) >= .5 True D defined as inlf != 0

Berdasarkan hasil diatas dapat disimpulkan:

o Specitivity : observasi hasil negative yang dinyatakan secara negative

secara benar sebesar 65.54%%

o Sensitivity : observasi hasil positive yang dinyatakan secara positive

secara benar sebesar 81.31%

o Secara Overall : model mampu menyatakan secara benar sebesar

74.50%

Untuk memperjelas hasil dari estimasi menggunakan Probit (prinlfhat) maka nilainya dapat kita gambarkan menggunakan scatter plot, dengan cara seperti berikut::

1. Membuat grafik Scatter Plot Transformasi Probit

Kita harus membuat variable baru, yaitu berisi ln dari (probabilitas/(1-probabilitas)), seperti yang tertera dalam grafik dalam membuat kurva transformasi Probit, deengan cara:

gen lnprinlfhat = ln(prinlfhat/(1-prinlfhat)) scatter prinlfhat inlf lnprinlfhat

(35)

2. Membuat Scatter Plot berdasarkan nilai Probabilitas Estimasi

menggunakan Probit, dengan cara:

sort prinlfhat gen idprobit = _n

scatter prinlfhat inlf idprobit

Dari hasil kedua scatter plot diatas menunjukkan bahwa nilai Transformasi probit dan Probabilitas Estimasi menggunakan probit

0 .2 .4 .6 .8 1 -6 -4 -2 0 2 4 lnprinlfhat

Pr(inlf) =1 if in lab frce, 1975

0 .2 .4 .6 .8 1 0 200 400 600 800 idprobit

(36)

(prinlfhat) tidak keluar dari nilai inlf aslinya, yaitu antara 0 dan 1. Berbeda dengan hasil dari LPM, namun sama dengan hasil menggunakan estimasi logit.

4. PERBANDINGAN ANTARA LOGIT DAN PROBIT DENGAN UJI

FITSTAT

fitstat, saving(L1) (Omitted)

fitstat, using(L1) force

Measures of Fit for probit of inlf

Current Saved Difference Model: probit logit

N: 753 753 0 Log-Lik Intercept Only: -514.873 -514.873 0.000 Log-Lik Full Model: -406.219 -406.143 -0.076 D: 812.438(746) 812.286(746) 0.151(0) LR: 217.309(6) 217.460(6) -0.151(0) Prob > LR: 0.000 0.000 0.000 McFadden's R2: 0.211 0.211 -0.000 McFadden's Adj R2: 0.197 0.198 -0.000 Maximum Likelihood R2: 0.251 0.251 -0.000 Cragg & Uhler's R2: 0.336 0.337 -0.000 McKelvey and Zavoina's R2: 0.388 0.354 0.034 Efron's R2: 0.261 0.261 -0.001 Variance of y*: 1.633 5.090 -3.457 Variance of error: 1.000 3.290 -2.290 Count R2: 0.745 0.742 0.003 Adj Count R2: 0.409 0.403 0.006 AIC: 1.098 1.097 0.000 AIC*n: 826.438 826.286 0.151 BIC: -4129.115 -4129.266 0.151 BIC': -177.564 -177.716 0.151

(37)

5. PERBANDINGAN ANTARA LPM. LOGIT, DAN PROBIT

MENGGUNAKAN GRAFIK SCATTER PLOT

• LPM dan Logit berdasarkan hasil estimasi (estimasi probabilitas)

scatter lpminlfhat inlf idlpmm ||scatter plgtinlfht inlf idlogit

• LPM dan Probit berdasarkan hasil estimasi (estimasi probabilitas)

scatter lpminlfhat inlf idlpmm || scatter prinlfhat inlf idprobit -. 5 0 .5 1 1. 5 0 200 400 600 800

Fitted values =1 if in lab frce, 1975 Pr(inlf) =1 if in lab frce, 1975

-. 5 0 .5 1 1. 5 0 200 400 600 800

Fitted values =1 if in lab frce, 1975 Pr(inlf) =1 if in lab frce, 1975

(38)

• Logit dan Probit berdasarkan hasil estimasi (estimasi probabilitas)

scatter plgtinlfht inlf idlogit || scatter prinlfhat inlf idprobit

• LPM, Logit dan Probit berdasarkan hasil estimasi (estimasi

probabilitas)

scatter lpminlfhat inlf idlpmm || scatter

plgtinlfht inlf idlogit || scatter prinlfhat inlf idprobit 0 .2 .4 .6 .8 1 0 200 400 600 800

Pr(inlf) =1 if in lab frce, 1975 Pr(inlf) =1 if in lab frce, 1975

-. 5 0 .5 1 1. 5 0 200 400 600 800

Fitted values =1 if in lab frce, 1975 Pr(inlf) =1 if in lab frce, 1975 Pr(inlf) =1 if in lab frce, 1975

(39)

• Grafik Transformasi Logit dan Probit

scatter plgtinlfht inlf lnplgtinlfht || scatter prinlfhat inlf lnprinlfhat

DAFTAR PUSTAKA

Gujarati, Damodar. 2006. Basic Econometrics. McGraw-Hill.

https://teaching.sociology.ul.ie/ https://wcr.sonoma.edu/

https://www.graphpad.com/

Manual Stata 11. 2009. Stata Press Publication, College Station, Texas

“Jika ada kritik dan saran atas modul ini, silahkan email ke

Segala kritik dan saran sangat berharga bagi penulis. ”

0 .2 .4 .6 .8 1 -6 -4 -2 0 2 4

Pr(inlf) =1 if in lab frce, 1975 Pr(inlf) =1 if in lab frce, 1975