BAB II DASAR TEORI
2.1 SALURAN TAK BUNDAR
Banyak saluran yang dibuat untuk memindahkan fluida berpenampang tidak bundar. Detil aliran pada saluran berpenampang persegi tergantung pada bentuk penampang yang sebenarnya dan banyak hasil dari pipa bundar dapat diterapkan pada aliran di dalam saluran dengan bentuk-bentuk yang lain.
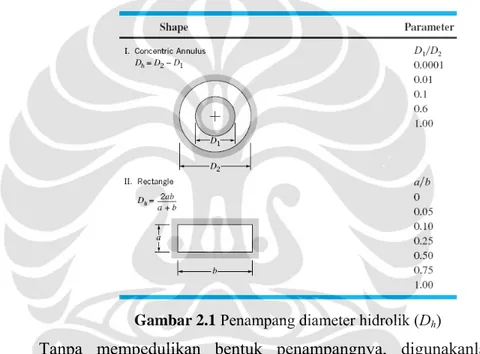
Gambar 2.1 Penampang diameter hidrolik (Dh)
Tanpa mempedulikan bentuk penampangnya, digunakanlah pendekatan diameter hidrolik untuk mengetahui diameter penampang selain bundar. Diameter hidrolik adalah empat kali rasio dari luas penampang aliran dibagi dengan keliling terbasahi (P) dari pipa. Diameter hidrolik mewakili suatu panjang karakteristik yang mendefinisikan ukuran sebuah penampang dari bentuk yang ditentukan. Faktor 4 ditambahkan dalam definisi Dh. Sehingga diameter hidrolik pipa berpenampang persegi sama dengan diameter pipa berpenampang bundar. Diameter hidrolik dapat didefinisikan sebagai :
(
2) ( )
4 4 4
h
A D
D D m
P D
π
= = π = (2.1)
Diameter hidrolik juga digunakan dalam definisi faktor gesekan :
( ) ( )
2 2
atau
2 2
L
h h
L u L pu
h f m p f Pa
D g D
⎛ ⎞ ⎛ ⎞
= ⎜ ⎟ Δ = ⎜ ⎟
⎝ ⎠ ⎝ ⎠ (2.2)
dan kekasaran relatif :
Dh
ε (2.3)
Pada saluran berpenampang tak bundar, interaksi antara dinding dan aliran bervariasi menurut posisi. Hal tersebut akan menghasilkan tegangan geser pada dinding yang tak seragam seperti pada Gambar 2.2 di bawah. Karena perubahan tekanan statik sepanjang saluran persegi adalah sama pada sepanjang aliran, maka sebuah mekanisme harus hadir untuk mengkompensasi perubahan tegangan geser dinding yang bervariasi. Mekanisme akan menyebabkan pembentukan aliran sekunder (secondary flow) yang memindahkan fluida dari daerah tegangan geser yang rendah ke daerah tegangan geser tinggi. Fenomena akan menghasilkan distribusi tegangan geser pada dinding dan menyebabkan pertukaran antara tekanan statik dan dinamik sehingga perubahan aliran terjadi antara daerah kecepatan rendah dan tinggi.
Gambar 2.2 Kontur kecepatan dan distribusi tegangan geser pada penampang seper- empat persegi
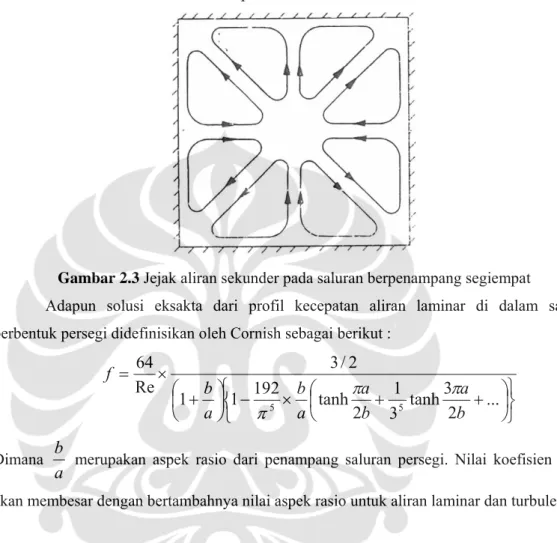
Gambar 2.3 di bawah menjelaskan jejak aliran dari aliran sekunder pada saluran berpenampang persegi. Kecepatan aliran sekunder mencapai angka maksimum sebesar 1-2 % dari kecepatan aksial.
Gambar 2.3 Jejak aliran sekunder pada saluran berpenampang segiempat
Adapun solusi eksakta dari profil kecepatan aliran laminar di dalam saluran berbentuk persegi didefinisikan oleh Cornish sebagai berikut :
⎭⎬
⎫
⎩⎨
⎧ ⎟
⎠
⎜ ⎞
⎝
⎛ + +
×
⎟ −
⎠
⎜ ⎞
⎝⎛ +
×
=
2 ...
tanh3 3
1 tanh2
1 192 1
2 / 3 Re
64
5
5 b
a b
a a
b a
f b
π π
π
(2.4)
Dimana a
b merupakan aspek rasio dari penampang saluran persegi. Nilai koefisien gesek
akan membesar dengan bertambahnya nilai aspek rasio untuk aliran laminar dan turbulen.
2.2 DAERAH MASUK DAN ALIRAN BERKEMBANG PENUH
Setiap fluida yang mengalir dalam sebuah pipa harus memasuki pipa pada suatu lokasi. Daerah aliran di dekat lokasi fluida memasuki pipa disebut sebagai daerah masuk (entrance region). Sebagaimana dnjukkan pada Gambar 2.4 di bawah, fluida biasanya memasuki pipa dengan profil kecepatan yang hampir seragam pada bagian (1). Selagi fluida bergerak melewati pipa, efek viskos menyebabkannya tetap menempel pada dinding pipa (kondisi lapisan batas tanpa-slip). Hal berlaku baik jika fluidanya adalah udara yang relatif inviscid ataupun minyak yang sangat viskos. Jadi, sebuah lapisan batas (boundary layer) di mana efek viskos menjadi penting timbul di
sepanjang dinding pipa sedemikian hingga profil kecepatan awal berubah menurut jarak sepanjang pipa (x) sampai fluida mencapai ujung akhir dari panjang daerah masuk di mana setelah di luar profil kecepatan tidak berubah lagi menurut x.
Bentuk dari profil kecepatan di dalam pipa tergantung pada apakah aliran laminar atau turbulen, sebagaimana pula panjang daerah masuk (le). Seperti pada banyak sifat lainnya dari aliran pipa, panjang masuk tak berdimensi le
⎛ D⎞
⎜ ⎟
⎝ ⎠
berkorelasi cukup baik dengan bilangan Reynolds. Panjang masuk pada umumnya diberikan oleh hubungan :
0,06 Re le
D = untuk aliran laminar (2.5)
dan
( )
164, 4 Re le
D = untuk aliran turbulen (2.6)
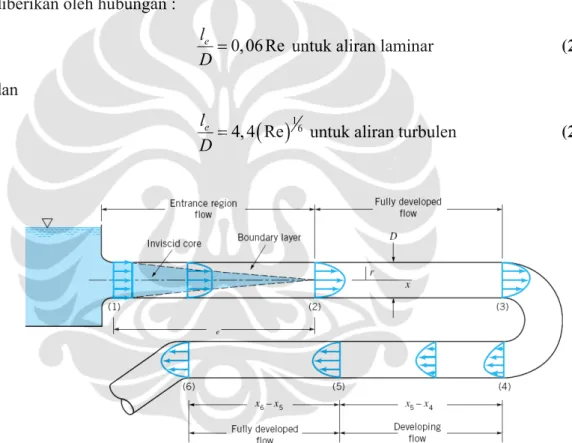
Gambar 2.4 Daerah masuk aliran sedang berkembang dan aliran berkembang penuh di dalam pipa
Perhngan profil kecepatan dan distribusi tekanan di dalam daerah masuk sangat rumit. Namun, apabila fluida telah mencapai ujung akhir dari daerah masuk, aliran lebih mudah digambarkan karena kecepatan hanyalah fungsi jarak dari sumbu pipa (r) dan tidak tergantung pada x. Hal berlaku sampai sifat dari pipa berubah karena sesuatu hal, misalnya perubahan diameter, atau sampai fluida mengalir
melalui sebuah belokan, katup, atau komponen lainnya pada bagian (3). Aliran antara (2) dan (3) disebut aliran berkembang penuh (fully developed). Setelah gangguan atas aliran berkembang penuh, aliran secara bertahap mulai kembali ke sifat berkembang penuhnya dan terus dengan profil sampai komponen pipa berikutnya dicapai [bagian (6)]. Dalam banyak kasus pipa cukup panjang sehingga terdapat panjang aliran berkembang penuh yang lebih besar dibandingkan dengan panjang aliran yang sedang berkembang
2.3 KERUGIAN TEKANAN ALIRAN DALAM PIPA
Kebanyakan analisis aliran pipa turbulen didasarkan pada data-data eksperimen dan rumus-rumus semiempiris, meskipun alirannya telah berkembang penuh. Hasil-hasil diberikan dalam bentuk tak berdimensi dan meliputi kisaran parameter aliran yang luas, termasuk berbagai fluida, pipa, dan laju aliran.
Penurunan tekanan dan kerugian head dalam sebuah pipa tergantung pada tegangan geser dinding (τw) antara fluida dan permukaan pipa. Sebuah perbedaan yang mendasar antara aliran laminar dan turbulen adalah bahwa tegangan geser untuk aliran turbulan adalah fungsi dari kerapatan fluida (ρ). Untuk aliran laminar, tegangan geser tidak tergantung pada kerapatan, sehingga hanya vikositas (μ) yang menjadi sifat fluida yang penting.
Meskipun penurunan tekanan untuk aliran pipa laminar tidak tergantung pada kekasaran pipa, namun ketika membahas aliran turbulen, parameter menjadi perlu diikutsertakan. Seperti yang diilustrasikan pada Gambar 2.5, aliran turbulen memiliki sebuah sublapisan viskos yang relatif tipis yang terbentuk pada fluida dekat dinding pipa. Dalam banyak hal, lapisan sangatlah tipis (δs/ D << 1, dimana δs adalah ketebalan sublapisan).
Gambar 2.5 Aliran pada sublapisan viskos (viscous sublayer) di dekat dinding kasar dan mulus
Parameter kekasaran pipa sering dipresentasikan sebagai faktor gesekan (friction factor). Persamaan dari faktor gesekan didapat dari persamaan Δp = 32μLu/D2 dan membagi kedua ruas dengan tekanan dinamik, ρu2/2, untuk mendapatkan bentuk tak berdimensi sebagai
(
2)
2 2
32 / 64
1 1 64 Re
2 2
p Lu D L L
uD D D
u u
μ μ
ρ ρ ρ
⎛ ⎞
Δ = = ⎜⎝ ⎟⎜ ⎟⎠⎛ ⎞⎝ ⎠= ⎛ ⎞⎜ ⎟⎝ ⎠ (2.7)
Bentuk sering dliskan sebagai
2
( )
2 p f L u Pa
D
Δ = ρ (2.8)
dimana bilangan tak berdimensinya (faktor gesekan) adalah
2
2
D u
f p
L ρ
⎛ ⎞
= Δ ⎛ ⎞⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠ (2.9)
Untuk aliran berkembang penuh laminar, nilai f secara sederhana dinyatakan sebagai
64
f =Re (2.10)
dan tidak tergantung pada ε/D. untuk aliran turbulen, ketergantungan fungsional dari faktor gesekan terhadap bilangan Reynolds dan kekasaran relatif (ε/D) agak rumit sehingga belum dapat diperoleh melalui analisis teoritis. Hasil-hasil diperoleh dari banyak eksperimen dan biasanya disajikan dalam bentuk rumus pencocokan kurva atau bentuk-bentuk grafik yang ekivalen.
Adapun persamaan energi untuk aliran tunak tak mampu-mampat adalah
2 2
1 1 2 2
1 1 2 2
2 2 L
p u p u
z z h
g g
α α
γ + + = γ + + + (2.11)
dimana hL adalah kerugian head antara bagian (1) dan (2). Dengan asumsi pipa berdiameter konstan (D1 = D2 sehingga u1 = u2), horizontal (z1 = z2) dengan aliran berkembang penuh (α1 = α2), persamaan menjadi Δ =p p1− p2 =γhL, yang dapat dikombinasikan dengan Persamaan (2.27) sehingga menghasilkan :
2 L 2
h f L u
= D g (2.12)
Persamaan (2.12) disebut sebagai persamaan Darcy-Weisbach yang berlaku untuk setiap aliran pipa tunak, tak mampu-mampat dan berkembang penuh baik jika pipa tersebut horizontal atau berada pada suatu kemiringan. Secara umum, dengan u1 = u2
persamaan energi memberikan
( ) ( )
2( )
1 2 2 1 2 1
L 2
p p z z h z z f L u Pa
D
γ γ γ ρ
− = − + = − + (2.13)
Sebagian dari perubahan tekanan disebabkan oleh perubahan ketinggian dan sebagian disebabkan oleh kerugian head yang berkaitan dengan efek gesekan, yang dinyatakan dalam faktor gesekan (f).
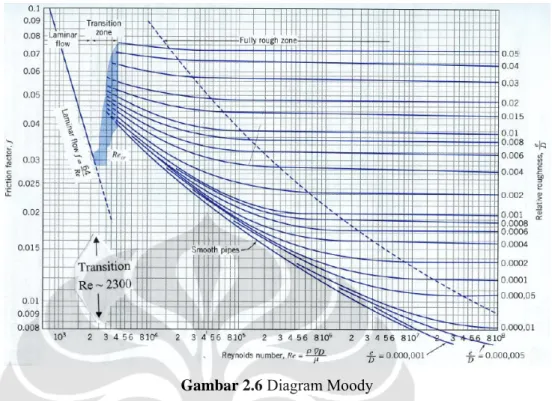
Gambar 2.6 Diagram Moody
Diagram Moody digunakan untuk menunjukkan ketergantungan fungsional f pada Re dan ε/D. Perlu diperhatikan bahwa nilai ε/D tidak perlu selalu bersesuaian dengan nilai aktual yang diperoleh melalui suatu penentuan mikroskopik dari ketinggian rata-rata kekasaran permukaan. Diagram Moody berlaku secara universal untuk semua aliran pipa yang tunak, berkembang penuh dan tak mampu-mampat.
Persamaan berikut dari Colebrook berlaku untuk seluruh kisaran non laminar dalam diagram Moody :
1 2, 0 log 2,51
3, 7 Re D
f f
⎛ε ⎞
= − ⎜⎜⎝ + ⎟⎟⎠ (2.14)
2.4 DARI PENERAPAN LANGSUNG F=ma PADA ELEMEN FLUIDA
Gambar 2.7 Gerakan elemen fluida silindris di dalam sebuah pipa
Gambar 2.8 Diagram benda-bebas dari silinder fluida
(p1)πr2−
(
p1−Δp)
πr2−( )
τ 2πrl=0 r lp =2τ
Δ (2.15)
h w
D τ r
τ = 2 (2.16)
h w
D p 4lτ
=
Δ (2.17)
Gambar 2.9 Distribusi tegangan geser pada fluida di dalam sebuah sebuah pipa (aliran laminar atau turbulen) dan profil-profil kecepatan yang khas
dr μdu
τ =− (2.18)
⎟⎟⎠
⎜⎜ ⎞
⎝
−⎛ Δ
= r
l p dr
du
μ 2
∫
∫
du=−⎜⎜⎝⎛ Δ2μpl⎟⎟⎠⎞ rdr1 2
4 r C
l u p⎟⎟⎠ +
⎜⎜ ⎞
⎝
−⎛ Δ
= μ
u = 0 pada r = Dh/2, jadi C1 = 2 16 Dh
l p ⎟⎟
⎠
⎜⎜ ⎞
⎝
⎛ Δ μ
u(r) = 2
16 Dh l p ⎟⎟
⎠
⎜⎜ ⎞
⎝
⎛ Δ
μ ⎥⎥⎦
⎤
⎢⎢
⎣
⎡
⎟⎟⎠
⎜⎜ ⎞
⎝
−⎛
⎥=
⎥
⎦
⎤
⎢⎢
⎣
⎡
⎟⎟⎠
⎜⎜ ⎞
⎝
−⎛
2
2 2
2 1 1
h c
h D
V r D
r (2.19)
Vc = 2
16 Dh l p ⎟⎟⎠
⎜⎜ ⎞
⎝
⎛ Δ μ
u(r) =
⎥⎥
⎦
⎤
⎢⎢
⎣
⎡ ⎟
⎠
⎜ ⎞
⎝
−⎛
2
4 1 R
Dh r
w
μ τ
R = Dh/2 adalah jari-jari pipa
Q = rdr
R V r
rdr r u udA
R R
r
r
c
∫
∫
∫
= = = ⎢⎢⎣⎡ −⎜⎝⎛ ⎟⎠⎞ ⎥⎥⎦⎤= 0
2
0
1 2 2
)
( π π
Atau Q = 2
2
Vc
πR
V = Q/A = Q/πr2
V = l
pD V
R V
R c c h
π μ π
32 2 2
2 2
2 = = Δ (2.20)
Q = l
p Dh
μ π
128
4Δ
(2.21)
A*V = l
p Dh
μ π
128
4Δ
Dh V 4 π 2
= l
p Dh
μ π
128
4Δ
gDh
L V p
2 Re 64 2 Δ =
γ , dimana f =
Re 64
gDh
L f V p
2
= 2
Δ
γ (2.22)
Berdasarkan hokum Bernoulli
hL
g z V z p
g V
p1 + 12 + 1 = 2 + 22 + 2+ 2
2 γ
γ V1 = V2
Z1 = Z2
γ γ
p p hL = p1− 2 = Δ
Δ =
− =
= γ γ
p p hL p1 2
gDh
L f V
2
2
jadi
L = h
gDh
L f V
2
2
(2.23)
2.5 Formula Teoretis Aliran Stream Line
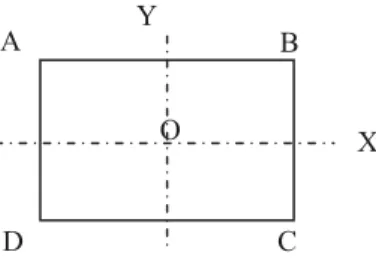
Formula dibuat dengan menggunakan sumbu koordinat pada penampang pipa, dimana OY merupakan garis sumbu yang sejajar dengan arah vertikal, OX pada arah horizontal dan OZ sejajar dengan sumbu pipa.
Gambar 2.10 Penampang Depan Saluran Persegi Panjang
Formula digunakan untuk mendapatkan faktor gesek menurut teori R.J.Cornish.
Rumus umum dan asumsi-asumsi yang digunakan antara lain adalah
⎟⎟⎠
⎜⎜ ⎞
⎝
⎛
∂ +∂
∂
= ∂
∂
= ∂
∂
= ∂
∂
∂
2 2 2 2
, 0 ,
0 y
w x
w z
p y
p x
p μ (2.24)
Dua persamaan pertama menunjukkan bahwa tekanan konstan di sepanjang penampang.
Misalkan
z p
∂
×∂
−
= μ
τ 2
1 , dan w=χ+τ
(
b2+y2)
Sebuah objek memperkenalkan χ sebagai penyederhanaan kondisi batas.
Sepanjang boundary χ+τ
(
b2−y2)
=w=0 (2.25) Untuk sepanjang AB dan CD χ =0 (2.26)Sedangkan sepanjang AD dan BC χ=−τ
(
b2−y2)
(2.27)Semua bentuk χ diubah ke bentuk
( )
b y n
2 1
cos 2 π
η + dimana η adalah fungsi x saja dan n adalah bilangan bundar.
2 0
2 2 2
∂ = +∂
∂
∂
y x
χ
χ (2.28)
Y
C D
A B
O X
2 0
2 2
=
∂ −
∂ χ η
x m (2.29) mx
B mx
Ancosh + nsinh
η = (2.30) Karena simetris terhadap Oy, Bn = 0; sehingga
mx Ancosh
η = (2.31) dan χ tersusun dari bentuk Ancoshmx×cosmy dimana m =
( )
b n
2 1 2 + π
π θ
y=2b (2.32)
maka
( )
π( )
θχ cos2 1
2 1 cosh 2
0
+ +
=
∑
=∞=
b n x A n
n n
n (2.33)
( ) ( )
2 2 2 2
4 4 4
π π θ θ τ
χ = = b −
f (2.34)
( )
π( )
θχ cos2 1
2 1 cosh 2
0
+ +
=
∑
=∞=
b n x A n
n n
n (2.35) Lalu kita ekspansi persamaan di atas dalam Deret Fourier.
Misalkan
( )
b( )
b( )
dalam(
a a)
f 4 ,
4 4 4
2 2 2 2 2
2 2
2 − = − −
=
= π
π θ τ π
π θ θ τ
χ (2.36)
( )
θ πθ dθa a n
f a
n
∑
∞ n=
⎟⎠
⎜ ⎞
⎝ + ⎛
=
,...
5 , 3 , 1
0 cos
2 (2.37) dimana
π
( )
θ π πθ θa d n n
f a na
a
n ⎟
⎠
⎜ ⎞
⎝
=2
∫
cos⎛0
(2.38)
( )
πθ θ πθ τπ
π τθ
πθ θ τπ
θ π τ
πθ θ π
π θ τ π
a d b n
a b n
a a n
a d b n
a b a n
a d n b
a na
a n
a n
a n
∫
∫
∫
⎭⎬
⎫
⎩⎨
⎧ ⎟
⎠
⎜ ⎞
⎝
− ⎛
⎟⎠
⎜ ⎞
⎝
= ⎛
⎟⎠
⎜ ⎞
⎝
− ⎛
=
⎟⎠
⎜ ⎞
⎝
− ⎛
=
0
2 2 2
2
2 2 2 0
2 0
2 2 2 2
cos cos
2 4
cos ) 4
2 (
4 cos 2
⎟⎠
⎜ ⎞
⎝ + ⎛
⎟⎠
⎜ ⎞
⎝
= ⎛
⎟⎠
⎜ ⎞
⎝
⎛
⎟×
⎠
⎜ ⎞
⎝
− ⎛
×
⎟−
⎠
⎜ ⎞
⎝
× ⎛
⎟ =
⎠
⎜ ⎞
⎝
⎛
⎟⎠
⎜ ⎞
⎝
− ⎛
⎟⎠
⎜ ⎞
⎝
× ⎛
⎟ =
⎠
⎜ ⎞
⎝
⎛
⎟×
⎠
⎜ ⎞
⎝
− ⎛
⎟⎠
⎜ ⎞
⎝
× ⎛
⎟ =
⎠
⎜ ⎞
⎝
⎛
∫
∫
∫
∫
∫
∫
a n n
a b a n n
a d b
a b n
n a a n n
a b a n n b a
a d b n
a d n n
a b a n n b a
a d b n
d a b
n n
a a
n n b a
a d b n
a a
a a
a a
πθ π
τθ πθ
π θ τθ τθ πθ
π πθ π
τθ πθ
τθ π πθ θ
τθ
πθ θ π
τθ πθ
τθ π πθ θ
τθ
θ πθ τθ
π πθ
τθ π πθ θ
τθ
8 cos 4 sin
cos 4
8 cos sin
4 cos
4
8 sin sin
4 cos
4
8 sin
sin 4
cos 4
2 2
2 2 2
2 0
2 2
2 2
2 0
2 2
0 2 2
2 0
2 2
2 0
2 2 0
2 2
πθ θ τπ
πθ θ
τπ d
a b n
a d b n
a
a
∫
∫
⎜⎝⎛ ⎟⎠⎞ = ⎜⎝⎛ ⎟⎠⎞0 2 2 0
2
2 cos cos
⎟⎠
⎜ ⎞
⎝
= ⎛
⎟⎠
⎜ ⎞
⎝
∫
b ⎛na d b n a naa τπ cos πθ θ τπ sin πθ
2
0 2
2
⎪⎭
⎪⎬
⎫
⎪⎩
⎪⎨
⎧ ⎟
⎠
⎜ ⎞
⎝
− ⎛
⎟⎠
⎜ ⎞
⎝ + ⎛
⎟⎠
⎜ ⎞
⎝
× ⎛
=
a a a
n a
n n
a b a n n
a b a
n n b a a a n
0 2
0 2
2 2 2
0 2
2 8 cos sin
sin
2 4 πθ τπ πθ
π τθ πθ
τθ π
π
⎭⎬
⎫
⎩⎨
⎧ ⎟
⎠
⎜ ⎞
⎝ + ⎛
⎟⎠
⎜ ⎞
⎝
− ⎛
⎟⎠
⎜ ⎞
⎝
− ⎛
⎟⎠
⎜ ⎞
⎝ + ⎛
⎟⎠
⎜ ⎞
⎝
− ⎛
⎟⎠
⎜ ⎞
⎝
= ⎛
a n n
a b a
a n n
a b a n n
a b a
a n n
a b a n n
a b a
a n n
a b a
an n2 4 sin 4 sin 0 8 cos 8 cos 0 2 sin 2 sin 0
2 2
2 2 2
2 2 2 2
2 2
2 π τπ π τπ π
π τθ π π τθ π π τθ π π τθ π
( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( )
⎭⎬
⎫
⎩⎨
⎧ + − −
=
⎭⎬
⎫
⎩⎨
⎧ − + − − +
=
τπ π π
π τθ π
π τθ π
τθ π
π τπ τπ π
π τθ π
τθ π
π τθ π
τθ π
n n a b n
a n b
n a n b
n a b a a n
n a n b
n a b n
a n b
n a b n
a n b
n a b a a n
n n
8 sin 8 cos
4 sin 2
0 sin sin
0 8 cos
8 cos 0 4 sin
4 sin 2
2 2 2
2 2 2
2 2 2 2
2
2 2
2 2
2 2 2
2 2 2 2
2 2
2
0 =0 a
⎭⎬
⎫
⎩⎨
⎧ − + −
−
= cos5 ...
5 3 1 3 cos cos 1
32
3 3
3
2 θ θ θ
π
χ τb (2.39)
(
2 2)
3 3
3 2
...
5 5 cos 3 1 3 cos cos 1
32 b b y
w + −
⎭⎬
⎫
⎩⎨
⎧ − + −
−
= θ θ θ τ
π
τ (2.40)
− −
∫ ∫
=
b
b a
a
wdxdy
Q (2.41)
( ) { ( ) }
( ) ( )
( ) { }
( )
( )
( )
dz dp dxdy ab
y b
ab ay
ab
ab ab
ay ab
ay y
ab ay
ab
y b a dx y b
x y b dx
y b
b a b b
b b b
a a a
τ μ
τ τ
τ
τ τ
τ τ
τ τ
τ τ
τ τ
τ τ
3
0 0
2 2
3 0
2 2
3 3
0
2 2
0 3 0
2 0
2 2
2 2 0
2 2
0 2 2 0
2 2
3 4 4
3 2 8
2 2
3 4 4
2 2
2
3 2 2
2 2
2 2
2 2
2 2
−
=
−
=
−
−
=
−
−
=
−
−
=
−
−
=
−
∫∫
∫
∫
∫
∫
∫
( ) ( )
( )
( ) ( ) ( )
( ) ( ) ( )
⎭⎬
⎫
⎩⎨
⎧ ⎟
⎠
⎜ ⎞
⎝
⎛ −
⎟ +
⎠
⎜ ⎞
⎝
⎛ +
= −
⎭⎬
⎫
⎩⎨
⎧ ⎟
⎠
⎜ ⎞
⎝
⎛ −
⎟+
⎠
⎜ ⎞
⎝
⎛ +
= −
⎟⎟⎠
⎜⎜ ⎞
⎝
− ⎛
=
∫ ∫
∫ ∫
∫ ∫
∫ ∫
∫ ∫
∫ ∫
∫ ∫
dxdy y b x dxdy n
y b x n b
a n n
wdxdy b
dxdy y
b x y n
b x n b
a n n
wdxdy b
b dxdy a n
b y n b x n wdxdy b
b a b a
b a
b a b a
b a b a
0 0 0 0
4 4
2
0 0
0 0 4 4
2
0 0
4 0 0
3 2
0 0
cosh 2 cosh 2
2 cosh 2 64
2
cosh 2 cosh 2
2 cosh 4 32
2 2
2 cosh
2 cos . 2 cosh 4 32
2 2
π π
π π
τ
π π
π π
τ
π π
π π
π τ
⎭ ⎬
⎫
⎩ ⎨
⎧ ⎟
⎠
⎜ ⎞
⎝
⎛ + • +
•
−
•
•
−
= ...
2 tanh 3 3
1 tanh 2
1 192 3
4
5 5
3
b a b
a a
b dz
dp
Q ab π π
π μ
untuk a = b, maka nilai
dz
dp Q=− •a •
μ 562 4 .
0 (2.42)
( )
⎭⎬
⎫
⎩⎨
⎧ ⎟
⎠
⎜ ⎞
⎝
⎛ + • +
•
− +
×
=
×
×
×
×
Δ
×
= ×
⎭⎬
⎫
⎩⎨
⎧ ⎟
⎠
⎜ ⎞
⎝
⎛ + • +
•
−
•
•
−
=
=
×
× ⎭⎬⎫
⎩⎨
⎧ ⎟
⎠
⎜ ⎞
⎝
⎛ + • +
•
−
•
•
−
=
×
= ×
−
−
−
−
2 ...
tanh3 3
1 tanh2
1 192 1
2 / 3 Re
64 2 Re
64
2 ...
tanh3 3
1 tanh2
1 192 1
3 1
4
2 ...
tanh3 3
1 tanh2
1 192 3
4 4
5 5
2 2
5 5
5 5
3
b a b
a a
f b
l u
p f m
b a b
a a
b dz
u dp b a
b a
b a b
a a
b dz
dp ab u
b a u Q
π π
ε π μ
π π
π μ
π π
π μ
(2.43)
Nilai faktor gesek yang diperoleh menggunakan persamaan eksplisit Colebrook-white dirumuskan dengan
f = 2
9 .
Re0
74 . 5 7 . log 3
25 . 0
⎥⎦
⎢ ⎤
⎣
⎡ ⎟
⎠
⎜ ⎞
⎝
⎛ +
D
ε (2.44)
Persamaan di atas untuk 10−6 ≤ ≤10−2 D
ε dan 5×103 ≤Re≤108