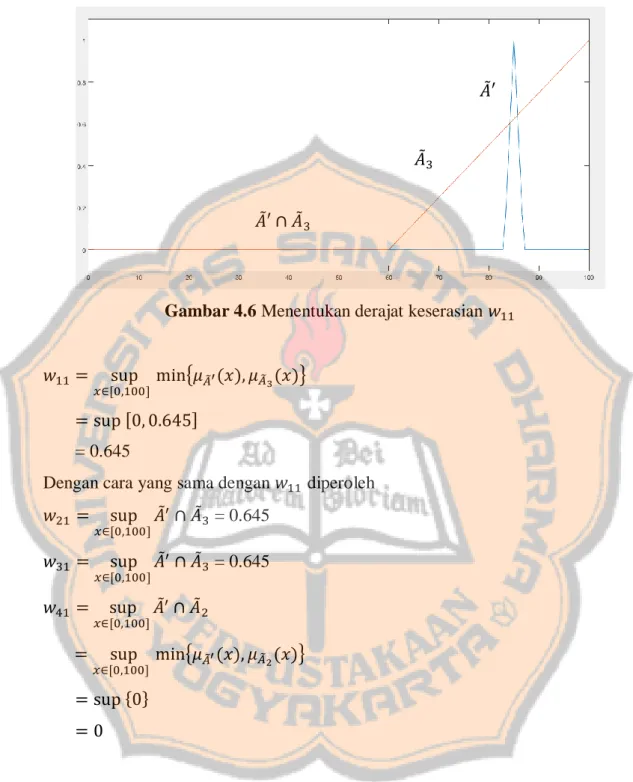
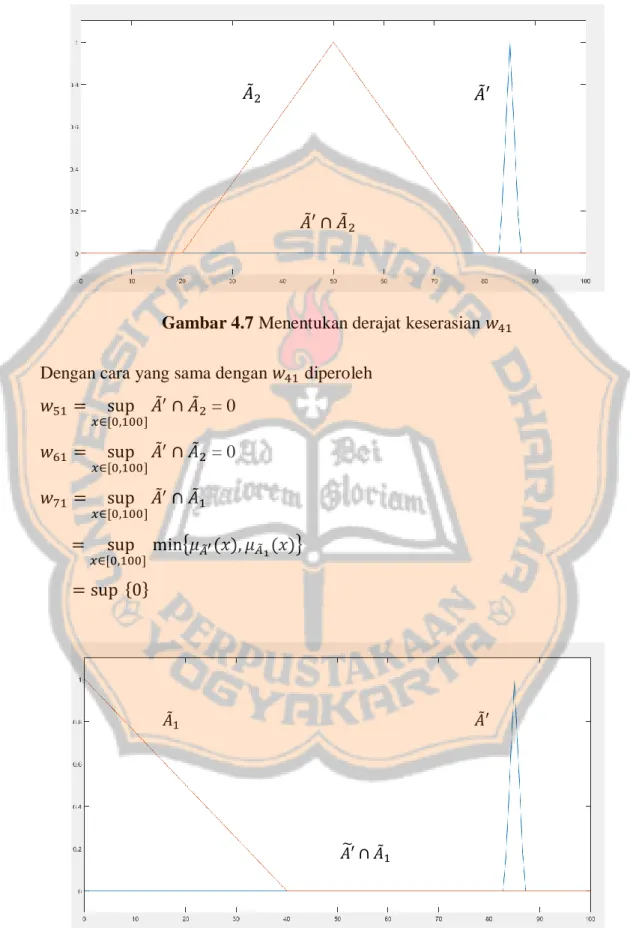
Aplikasi sistem inferensi kabur mamdani dalam pengaturan kecerahan layar telpon genggam

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. APLIKASI SISTEM INFERENSI KABUR MAMDANI DALAM PENGATURAN KECERAHAN LAYAR TELPON GENGGAM Skripsi Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika Program Studi Matematika. Oleh: Florens Septiane Trisnanta NIM: 153114012 PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI UNIVERSITAS SANATA DHARMA YOGYAKARTA 2019. i.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. APPLICATION OF MAMDANI FUZZY INFERENCE SYSTEM IN MOBILE PHONE SCREEN BRIGTHNESS SETTING. Thesis Presented as Partipal Fulfillment of the Requirements to Obtain the Degree of Sarjana Sains Mathematics Study Program. Written by: Florens Septiane Trisnanta Student ID: 153114012. MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY SANATA DHARMA UNIVERSITY YOGYAKARTA 2019. ii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. MOTTO “Janganlah hendaknya kamu kuatir tentang apa pun juga, tetapi nyatakanlah dalam segala hal keinginanmu kepada Allah dalam doa dan permohonan dengan ucapan syukur” (Filipi 4:6). vi.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. HALAMAN PERSEMBAHAN. Karya ini kupersembahkan untuk: Tuhan Yesus Kristus, kedua orang tuaku dan keluargaku.. vii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. ABSTRAK. Logika kabur pertama kali diperkenalkan oleh Prof. Lotfi A. Zadeh pada tahun 1965. Nilai kebenaran dalam logika kabur dinyatakan dengan suatu bilangan real dalam selang tertutup [0,1]. Sistem inferensi kabur adalah sistem komputasi yang bekerja atas dasar penalaran kabur. Dalam tugas akhir ini digunakan salah satu sistem inferensi, yaitu sistem inferensi Mamdani, untuk menetapkan tingkat kecerahan layar pada telpon genggam. Faktor-faktor yang dipertimbangkan untuk memutuskan tingkat kecerahan layar telpon genggam, yaitu kondisi cahaya ruangan dan jarak pemakai telpon genggam. Kedua faktor tersebut yang menjadi variabel masukan pada sistem inferensi ini.. Kata kunci: Logika kabur, sistem inferensi kabur Mamdani, tingkat kecerahan layar telpon genggam.. ix.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. ABSTRACT. Fuzzy logic was first introduced by Prof. Lotfi A. Zadeh in 1965. Truth value in fuzzy logic is expressed by a real number in the closed interval [0,1]. Fuzzy inference system is a computation system based on fuzzy reasoning. In this final paper one of the fuzzy inference system is used, i.e. the Mamdani inference system, to set the brightness level of a mobile phone’s screen. The factors are considered to decide the brightness level of a mobile phone’s screen are the conditions of room light and the distance of mobile phone’s user. Both factors are the input variables in this system.. Keywords: Fuzzy logic, Mamdani fuzzy inference system, brightness level of a mobile phone’s screen. x.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. KATA PENGANTAR. Puji dan syukur kepada Tuhan Yesus Kristus atas segala kasih, berkat, dan karunia-Nya sehingga penulis dapat menyelesaikan skripsi ini dengan baik. Skripsi ini dibuat dengan tujuan memenuhi syarat untuk memperoleh gelar Sarjana Sains pada Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma. Dalam penulisan skripsi ini, penulis menyadari bahwa penulis melibatkan banyak pihak yang bersedia membantu dalam berbagai macam kesulitan. Penulis juga tidak lepas dari dukungan dari banyak pihak. Oleh karena itu, pada kesempatan ini penulis mengucapkan terima kasih kepada: 1. Prof. Dr. Frans Susilo, SJ selaku dosen pembimbing skripsi yang selalu sabar memberikan arahan kepada penulis untuk menyelesaikan tugas akhir ini. 2. Bapak Sudi Mungkasi, S.Si, M.Math.Sc., Ph.D., selaku Dekan Fakultas Sains dan Teknologi dan selaku Dosen Pembimbing Akademik. 3. Bapak Hartono, S.Si., M.Sc., Ph.D., selaku Kaprodi Matematika. 4. Bapak Ir. Ig. Aris Dwiatmoko, M.Sc, Bapak Dr. rer. nat. Herry Pribawanto Suryawan, S.Si., M.Si., Bapak Ricky Aditya, M.Sc, dan Ibu Maria Vianney Any Herawati, S.Si., M.Si., selaku dosen-dosen Prodi Matematika yang telah memberikan banyak ilmu pengetahuan kepada penulis selama proses perkuliahan. 5. Bapak/Ibu dosen/karyawan Fakultas Sains dan Teknologi yang telah berdinamika bersama selama penulis berkuliah. 6. Kedua orang tua, kakak, saudara dan keluarga yang telah mendoakan, membantu dan mendukung penulis selama proses pengerjaan skripsi. 7. Sahabat Penulis yang sudah meluangkan waktunya untuk mendengarkan keluh kesah, dan memberi dukungan serta motivasi dari awal penulisan sampai akhir penulisan skripsi ini, yakni Marsella Novita.. xi.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. DAFTAR ISI. HALAMAN JUDUL ........................................................................................ i HALAMAN JUDUL DALAM BAHASA INGGRIS ...................................... ii HALAMAN PERSETUJUAN PEMBIMBING .............................................. iii HALAMAN PENGESAHAN ........................................................................ iv PERNYATAAN KEASLIAN KARYA ........................................................... v MOTTO..............................................................................................................vi HALAMAN PERSEMBAHAN .................................................................... vii LEMBAR PERNYATAAN PERSETUJUAN .............................................. viii ABSTRAK ..................................................................................................... ix ABSTRACT.................................................................................................... x KATA PENGANTAR .................................................................................... xi DAFTAR ISI................................................................................................ xiii BAB I PENDAHULUAN ............................................................................... 1 A. Latar Belakang ....................................................................................... 1 B. Rumusan Masalah .................................................................................. 3 C. Batasan masalah ..................................................................................... 3 D. Tujuan penulisan .................................................................................... 3 E. Metode penulisan ................................................................................... 3 F. Manfaat penulisan .................................................................................. 3 G. Sistematika penulisan ............................................................................. 4 BAB II HIMPUNAN KABUR ........................................................................ 6 A. Konsep Himpunan Kabur ....................................................................... 6 xiii.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. B. Fungsi Keanggotaan ............................................................................. 10 C. Operasi-Operasi pada Himpunan Kabur ............................................... 15 D. Relasi Kabur ...................................................................................... 23 BAB III LOGIKA KABUR ........................................................................... 26 A. Variabel Linguistik ............................................................................... 26 B. Pengubah Linguistik ............................................................................. 27 C. Proposisi Kabur .................................................................................... 28 D. Implikasi Kabur.................................................................................... 30 E. Penalaran Kabur ................................................................................... 32 F. Sistem Inferensi Kabur ......................................................................... 37 1. Unit Pengaburan .............................................................................. 38 2. Unit Basis Pengetahuan ................................................................... 39 3. Unit Penalaran Kabur ...................................................................... 40 4. Unit Penegasan ................................................................................ 40 BAB IV APLIKASI SISTEM INFERENSI KABUR MAMDANI ................ 43 A. Sistem Inferensi Kabur Mamdani ......................................................... 43 B. Implementasi Sistem Inferensi Kabur Mamdani Pada Pengaturan Kecerahan Layar Telpon Genggam ...................................................... 43 1. Pembentukan Himpunan Kabur ....................................................... 43 2. Basis Kaidah.................................................................................... 47 3. Unit Pengaburan .............................................................................. 48 4. Unit Penalaran Kabur ...................................................................... 50 5. Unit Penegasan ................................................................................ 60 BAB V PENUTUP ........................................................................................ 61 A. Kesimpulan .......................................................................................... 61. xiv.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. B. Saran .................................................................................................... 63 DAFTAR PUSTAKA.................................................................................... 64. xv.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB I PENDAHULUAN. A. Latar Belakang Perkembangan teknologi saat ini semakin maju. Salah satunya di bidang teknologi komunikasi, yaitu telpon genggam. Telpon genggam yang pada awalnya merupakan barang langka dan mewah serta hanya orang dari kalangan ekonomi atas yang memilikinya. Namun, seiring perkembangan zaman, telpon genggam menjadi kebutuhan dan mudah dibeli. Telpon genggam saat ini sudah menjadi bagian dari gaya hidup masyarakat modern. Hampir setiap orang memiliki telpon genggam sebagai alat komunikasi mereka. Keberadaan telpon genggam saat ini tidak hanya digunakan oleh orang dewasa saja, namun anak-anak pun sudah banyak yang memiliki telpon genggam. Bahkan masyarakat sekarang tidak dapat dipisahkan oleh telpon genggam. Telpon genggam dapat membantu seseorang melakukan komunikasi dengan cepat. Tetapi pemakaian telpon genggam yang terlampau lama dapat menimbulkan dampak negatif bagi kesehatan, terutama kesehatan mata. Masalah kesehatan mata ini tidak lepas dari peran cahaya karena cahaya yang menimpa benda tersebut akan dipantulkan ke mata untuk dapat terlihat. Aktivitas pada saat menggunakan telpon genggam harus memperhatikan penerangan yang cukup, sebab dalam jangka waktu lama akan berdampak pada kelelahan mata jika tidak diimbangi dengan intensitas penerangan yang memadai. Oleh karena itu, kecerahan pada layar telpon genggam menjadi bagian yang penting dalam penggunaan telpon genggam. Kecerahan layar telpon genggam dapat diatur dengan menerapkan logika kabur. Logika kabur pertama kali diperkenalkan oleh Prof. Lotfi A. Zadeh pada tahun 1965. Nilai kebenaran dalam logika kabur dinyatakan dengan suatu bilangan real dalam selang tertutup [0,1]. Dasar dari logika kabur adalah himpunan kabur. Pada teori himpunan kabur, peranan derajat keanggotaan sebagai penentu keberadaan elemen dalam suatu himpunan sangatlah penting. Salah satu aplikasi logika kabur. 1.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 2. yang telah berkembang amat luas dewasa ini adalah dalam sistem inferensi kabur, yaitu sistem komputasi yang bekerja atas dasar penalaran kabur, misalnya sistem kendali otomatis, sistem klasifikasi data, sistem pakar, sistem pengenalan pola, robotika, dan sebagainya (Susilo, 2018). Sistem inferensi kabur yang banyak dikenal diantaranya adalah sistem inferensi kabur Mamdani, sistem inferensi kabur Tsukamoto, dan sistem inferensi kabur Takagi-Sugeno-Kang. Sistem inferensi kabur Mamdani atau biasa dikenal sebagai metode MinMax merupakan suatu metode menggunakan aturan “Jika-Maka”. Sistem inferensi kabur Mamdani ini diperkenalkan oleh Ebrahim Mamdani pada tahun 1974. Sistem inferensi kabur Mamdani dapat memberikan solusi yang baik untuk menentukan tingkat kecerahan layar telpon genggam dengan kondisi tertentu. Pada tugas akhir ini, sistem inferensi kabur Mamdani akan dipakai untuk menentukan tingkat kecerahan pada layar telpon genggam berdasarkan terangnya ruangan dan jarak pemakai dengan telpon genggam. Permasalahan ini hanya terdiri dari dua masukan saja, yaitu terangnya ruangan dan jarak pemakai dengan telpon genggam. Nilai linguistik untuk variabel “terangnya ruangan” ada tiga macam, yaitu : 1.. Terang. 2.. Sedang. 3.. Gelap. Sedangkan variabel “jarak pemakai dengan telpon genggam” mempunyai tiga nilai linguistik, yaitu : 1.. Jauh. 2.. Sedang. 3.. Dekat. Varibel keluaran, yaitu “tingkat kecerahan layar pada telpon genggam” mempunyai tiga nilai linguistik, yaitu rendah, sedang, dan tinggi. Untuk mendapatkan keluaran diperlukan empat tahapan: 1.. Menentukan semua variabel terkait, baik variabel masukan maupun variabel keluaran.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 3. 2.. Membentuk basis kaidah. 3.. Menarik kesimpulan. 4.. Mengubah kesimpulan yang masih berupa himpunan kabur menjadi suatu nilai tegas dengan menggunakan fungsi penegasan. B. Rumusan Masalah Masalah yang diangkat dalam skripsi ini adalah bagaimana menerapkan sistem inferensi kabur Mamdani untuk mengatur tingkat kecerahan layar telpon genggam dengan dua variabel masukan, yaitu terangnya ruangan dan jarak pemakai dengan telpon genggam?. C. Batasan masalah Dalam tugas akhir ini, penulis akan membatasi penulisan agar lebih terarah dan tidak menyimpang dari masalah yang akan dibahas, yaitu: 1. Metode yang digunakan yaitu metode Mamdani. 2. Masukannya adalah terangnya ruangan dan jarak pemakai dengan telpon genggam.. D. Tujuan penulisan Tujuan penulisan tugas akhir ini adalah untuk menentukan tingkat kecerahan layar telpon genggam dengan menggunakan sistem inferensi kabur Mamdani.. E. Metode penulisan Metode penulisan yang digunakan untuk menyusun tugas akhir ini adalah studi pustaka, yaitu dengan membaca dan mempelajari jurnal-jurnal, makalah, dan buku-buku yang berkaitan dengan sistem inferensi kabur Mamdani.. F. Manfaat penulisan Manfaat penulisan tugas akhir ini adalah:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 4. 1.. Penulis dan pembaca mendapat gambaran tentang penerapan sistem inferensi kabur Mamdani untuk mengatur tingkat kecerahan layar telpon genggam.. 2. Tugas akhir ini dapat dijadikan referensi bagi peneliti lain.. G. Sistematika penulisan Sistematika penulisan tugas akhir ini adalah sebagai berikut: BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Metode Penulisan F. Manfaat Penulisan G. Sistematika Penulisan BAB II HIMPUNAN KABUR A. Konsep Himpunan Kabur B. Fungsi Keanggotaan C. Operasi-operasi pada Himpunan Kabur D. Relasi Kabur BAB III LOGIKA KABUR A. Variabel Linguistik B. Pengubah Linguistik C. Proposisi Kabur D. Implikasi Kabur E. Penalaran Kabur F. Sistem Inferensi Kabur BAB IV APLIKASI SISTEM INFERENSI KABUR MAMDANI A. Sistem Inferensi Kabur Mamdani B. Implementasi Sistem Inferensi Kabur Mamdani Pada Pengaturan Kecerahan Layar Telpon Genggam BAB V PENUTUP.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 5. A. Kesimpulan B. Saran DAFTAR PUSTAKA.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB II HIMPUNAN KABUR. A. Konsep Himpunan Kabur Himpunan tegas adalah himpunan yang terdefinisi secara tegas, dalam arti bahwa untuk setiap elemen dalam semestanya selalu dapat ditentukan secara tegas apakah ia merupakan anggota himpunan itu atau tidak. Dengan kata lain, terdapat batas tegas antara unsur-unsur yang merupakan anggota dan unsur-unsur yang tidak merupakan anggota. Tetapi tidak semua himpunan dapat didefiniskan secara demikian, misalnya himpunan orang kaya, himpunan orang pandai, himpunan orang miskin, dan sebagainya. Himpunan semacam itu disebut himpunan kabur (fuzzy set). Zadeh mengaitkan himpunan semacam itu dengan suatu fungsi yang menyatakan derajat kesesuaian unsur-unsur dalam semestanya dengan konsep yang merupakan syarat keanggotaan himpunan tersebut. Fungsi itu disebut fungsi keanggotaan dan nilai fungsi itu disebut derajat keanggotaan suatu unsur dalam himpunan itu. Derajat keanggotaan itu dinyatakan dengan suatu bilangan real dalam selang tertutup [0,1]. Definisi 2.1.1 Suatu himpunan kabur 𝐴̃ dalam semesta wacana X adalah himpunan yang mempunyai fungsi keanggotaan yang dinyatakan dalam pemetaan 𝜇𝐴̃ dari X ke selang [0,1], yaitu 𝜇𝐴̃ ∶ 𝑋 → [0,1]. Nilai fungsi 𝜇𝐴̃ (𝑥) menyatakan derajat keanggotaan unsur 𝑥 ∈ 𝑋 dalam himpunan kabur 𝐴̃ . Nilai fungsi sama dengan 1 menyatakan keanggotaan penuh, sedangkan nilai fungsi sama dengan 0 menyatakan sama sekali bukan anggota himpunan kabur tersebut. Oleh karena itu, himpunan tegas juga dapat dipandang sebagai kejadian. 6.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 7. khusus dari himpunan kabur, yaitu himpunan kabur yang fungsi keanggotaannya hanya bernilai 0 atau 1 saja. Suatu himpunan kabur 𝐴̃ dalam semesta wacana X dapat dinyatakan sebagai himpunan pasangan terurut 𝐴̃ = {(𝑥, 𝜇𝐴̃ (𝑥))| 𝑥 ∈ 𝑋} dimana 𝜇𝐴̃ adalah fungsi keanggotaan dari himpunan kabur 𝐴̃ . Jika X kontinu maka himpunan kabur 𝐴̃ seringkali ditulis 𝑟. 𝐴̃ = ∫ 𝜇𝐴̃ (𝑥 )/𝑥 𝑥∈𝑋. dimana lambang ʃ bukan lambang integral seperti yang dikenal dalam kalkulus, tetapi melambangkan keseluruhan unsur-unsur 𝑥 ∈ 𝑋 bersama dengan derajat keanggotaannya dalam himpunan kabur 𝐴̃ dan lambang / tidak melambangkan operasi pembagian yang dikenal dalam aritmetika, tetapi melambangkan pasangan unsur 𝑥 dan derajat keanggotaannya. Jika X diskret maka himpunan kabur 𝐴̃ sering kali ditulis 𝐴̃ = ∑ 𝜇𝐴̃ (𝑥 )/𝑥 𝑥∈𝑋. dimana lambang ∑ di sini tidak melambangkan operasi jumlahan yang dikenal dalam aritmetika, tetapi melambangkan keseluruhan unsur-unsur 𝑥 ∈ 𝑋 bersama dengan derajat keanggotaannya dalam himpunan kabur 𝐴̃ dan lambang / tidak melambangkan operasi pembagian yang dikenal dalam aritmetika, tetapi melambangkan pasangan unsur 𝑥 dan derajat keanggotaannya. Definisi 2.1.2 ̃ yang dilambangkan dengan Pend(𝐴̃ ), Pendukung dari suatu himpunan kabur 𝐴, adalah himpunan tegas yang memuat semua unsur dari semesta yang mempunyai derajat keanggotaan taknol dalam 𝐴̃ , yaitu: 𝑃𝑒𝑛𝑑(𝐴̃ ) = {𝑥 ∈ 𝑋 │ 𝜇𝐴̃ (𝑥 ) > 0}..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 8. Definisi 2.1.3 ̃ yang dilambangkan dengan 𝑇𝑖𝑛𝑔𝑔𝑖(𝐴̃ ), Tinggi dari suatu himpunan kabur 𝐴, didefinisikan sebagai 𝑇𝑖𝑛𝑔𝑔𝑖 (𝐴̃ ) = sup{𝜇𝐴̃ (𝑥)}. 𝑥∈𝑋. Himpunan kabur yang mempunyai tinggi sama dengan satu disebut himpunan kabur normal, sedangkan himpunan kabur yang mempunyai tinggi kurang dari satu disebut himpunan kabur subnormal. Definisi 2.1.4 Titik silang dari suatu himpunan kabur 𝐴̃ adalah anggota dari semesta yang mempunyai derajat keanggotaan sama dengan 0.5. Definisi 2.1.5 Teras dari suatu himpunan kabur 𝐴̃ , yang dilambangkan dengan 𝑇𝑒𝑟𝑎𝑠(𝐴̃ ), adalah himpunan tegas yang memuat semua unsur dari semestanya yang mempunyai derajat keanggotaan sama dengan 1, yaitu 𝑇𝑒𝑟𝑎𝑠(𝐴̃ ) = {𝑥 ∈ 𝑋 │ 𝜇𝐴̃ (𝑥 ) = 1}. Definisi 2.1.6 Pusat dari suatu himpunan kabur didefinisikan sebagai berikut: Jika nilai purata dari semua titik dimana fungsi keanggotaan himpunan kabur itu mencapai nilai maksimum adalah berhingga, maka pusat himpunan kabur itu adalah nilai purata tersebut. Jika purata itu takhingga positif (negatif) , maka pusat himpunan kabur itu adalah yang terkecil (terbesar) diantara semua titik yang mencapai nilai fungsi keanggotaan maksimum. Contoh 2.1.1 Dalam semesta 𝑋 = {−4, −3, −2, −1, 0, 1, 2, 3,4}, himpunan kabur 𝐴̃ dapat dinyatakan misalnya sebagai.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 9. 𝐴̃ = ∑ 𝜇𝐴̃ (𝑥 )⁄𝑥 𝑥∈𝑋. = 0.3⁄−3 + 0.5⁄−2 + 0.8⁄−1 + 1⁄0 + 0.8⁄1 + 0.5/2 + 0.3/3 Bilangan −4 dan 4 mempunyai derajat keanggotaan 0 yang biasanya tidak ditulis dalam penyajian himpunan kabur dengan semesta diskret. 𝑃𝑒𝑛𝑑(𝐴̃ ) = {−3, −2, −1 , 0 , 1, 2, 3}. 𝑇𝑖𝑛𝑔𝑔𝑖(𝐴̃ ) = 1; himpunan kabur 𝐴̃ ini adalah himpunan kabur normal. Titik silang dari himpunan kabur 𝐴̃ ini adalah −2 dan 2. 𝑇𝑒𝑟𝑎𝑠(𝐴̃ ) = {0}. Definisi 2.1.7 Dua buah himpunan kabur 𝐴̃ dan 𝐵̃ dalam semesta X dikatakan sama, dinotasikan ̃ bila dan hanya bila dengan 𝐴̃ = 𝐵, 𝜇 𝐴̃ (𝑥 ) = 𝜇𝐵̃ (𝑥 ), ∀ 𝑥 ∈ 𝑋. Definisi 2.1.8 Dalam semesta X, himpunan kabur 𝐴̃ disebut himpunan bagian dari himpunan ̃ bila dan hanya bila kabur 𝐵̃ , yaitu 𝐴̃ ⊆ 𝐵, 𝜇𝐴̃ (𝑥 ) ≤ 𝜇𝐵̃ (𝑥 ), ∀ 𝑥 ∈ 𝑋. Jadi, 𝐴̃ = 𝐵̃ bila dan hanya bila 𝐴̃ ⊆ 𝐵̃ dan 𝐵̃ ⊆ 𝐴̃ . Contoh 2.1.2 Jika 𝐴̃ = 0.3/−3 + 0.5/−2 + 0.8/−1 + 1/0 + 0.8/1 + 0.5/2 + 0.3/3 dan 𝐵̃ = 0.4/−3 + 0.6/−2 + 0.9/−1 + 1/0 + 0.9/1 + 0.6/2 + 0.4/3, maka 𝐴̃ ⊆ 𝐵̃ ..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 10. B. Fungsi Keanggotaan. Setiap himpunan kabur dapat dinyatakan dengan suatu fungsi keanggotaan. Ada beberapa cara yang digunakan untuk menyatakan himpunan kabur dengan fungsi keanggotaannya. Untuk semesta hingga diskret biasanya dipakai cara daftar, yaitu daftar anggota-anggota semesta bersama dengan derajat keanggotaannya. Misalnya diberikan semesta 𝑋 = {Surya, Boby, Shintia, Bagas, Desi} yang terdiri dari mahasiswa dengan indeks prestasi berturut-turut 3.5, 2.6, 3.8, 1.7, dan 2.9. Himpunan kabur 𝐴̃ = “himpunan mahasiswa yang pandai” dapat dinyatakan dengan cara daftar sebagai berikut: 𝐴̃ = 0.8/Surya + 0.6/Boby + 0.9/Shintia + 0.4/Bagas + 0.7/Desi.. Untuk semesta takhingga yang kontinu, cara yang paling sering digunakan adalah cara analitik, yaitu mempresentasikan fungsi keanggotaan himpunan kabur dalam bentuk suatu formula matematis yang dapat disajikan dalam bentuk grafik. Misalnya 𝐴̃ adalah himpunan kabur “bilangan real yang dekat dengan 2”. Maka 𝐴̃ dapat disajikan dalam bentuk 𝑟 2 𝐴̃ = ∫ 𝑒 −(𝑥−2) ⁄𝑥. 𝑥∈𝑅. dimana 𝜇𝐴̃ (𝑥 ) = 𝑒. −(𝑥−2)2. adalah fungsi keanggotaan 𝐴̃ .. Bilangan 2 mempunyai derajat keanggotaan penuh sama dengan 1, yaitu 𝜇𝐴̃ (2) = 1, sedangkan 1 dan 3 mempunyai derajat keanggotaan 0.37, yaitu 𝜇𝐴̃ (1) = 𝜇𝐴̃ (3) = 0.37. Himpunan kabur 𝐴̃ = "bilangan real yang dekat dengan 2" itu juga dapat dinyatakan dengan fungsi keanggotaan sebagai berikut 𝑥−1 𝜇𝐴̃ (𝑥 ) = {3 − 𝑥 0. untuk 1 ≤ 𝑥 ≤ 2 untuk 2 ≤ 𝑥 ≤ 3 untuk 𝑥 lainnya.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 11. dengan. derajat. keanggotaan. 𝜇𝐴̃ (2) = 1, 𝜇 𝐴̃ (1.5) = 𝜇𝐴̃ (2.5) = 0.5, 𝜇 𝐴̃ (1) =. 𝜇 𝐴̃ (3) = 0. Kebanyakan himpunan kabur berada dalam semesta himpunan semua bilangan real ℝ dengan fungsi keanggotaan yang dinyakatan dalam bentuk suatu formula matematis. Beberapa fungsi keanggotaan himpunan kabur yang sering digunakan adalah sebagai berikut: 1. Fungsi Keanggotaan Segitiga Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan segitiga jika mempunyai tiga buah parameter, yaitu a, b, c ∈ ℝ dengan a < b < c, dan dinyatakan dengan Segitiga (x; a, b, c) dengan aturan: 𝑥−𝑎 untuk 𝑎 ≤ 𝑥 ≤ 𝑏 𝑏−𝑎 𝑆𝑒𝑔𝑖𝑡𝑖𝑔𝑎 (𝑥; 𝑎, 𝑏, 𝑐 ) = 𝑐 − 𝑥 untuk 𝑏 ≤ 𝑥 ≤ 𝑐 𝑐−𝑏 0 untuk 𝑥 lainnya { Fungsi keanggotaan tersebut dapat juga dinyatakan dengan formula sebagai berikut: 𝑆𝑒𝑔𝑖𝑡𝑖𝑔𝑎 (𝑥; 𝑎, 𝑏, 𝑐 ) = max (min (. 𝑥−𝑎 𝑐 −𝑥 , ) , 0) . 𝑏−𝑎 𝑐 −𝑏. Contoh 2.2.1 Misalkan diketahui fungsi keanggotaan Segitiga (x; 15, 25, 35), maka grafik fungsi tersebut adalah. Gambar 2.1 Fungsi Keanggotaan Segitiga (x; 15, 25, 35).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 12. 2. Fungsi Keanggotaan Trapesium Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan trapesium jika mempunyai empat buah parameter, yaitu a, b, c, d ∈ ℝ dengan a < b < c < d, dan dinyatakan dengan Trapesium (x; a, b, c, d) dengan aturan: 𝑥−𝑎 untuk 𝑎 ≤ 𝑥 ≤ 𝑏 𝑏−𝑎 1 untuk 𝑏 ≤ 𝑥 ≤ 𝑐 𝑇𝑟𝑎𝑝𝑒𝑠𝑖𝑢𝑚 (𝑥; 𝑎, 𝑏, 𝑐, 𝑑 ) = 𝑑 − 𝑥 untuk 𝑐 ≤ 𝑥 ≤ 𝑑 𝑑 −𝑐 { 0 untuk 𝑥 lainnya Fungsi keanggotaan tersebut dapat juga dinyatakan dengan formula sebagai berikut: 𝑇𝑟𝑎𝑝𝑒𝑠𝑖𝑢𝑚 (𝑥; 𝑎, 𝑏, 𝑐, 𝑑 ) = max (min (. 𝑥−𝑎 𝑑 −𝑥 , 1, ) , 0). 𝑏−𝑎 𝑑−𝑐. Contoh 2.2.2 Misalkan diketahui fungsi keanggotaan Trapesium (x; 40, 60, 90, 100), maka grafik fungsi keanggotaan tersebut adalah. Gambar 2.2 Fungsi Keanggotaan Trapesium (x; 40, 60, 90, 100) 3. Fungsi Keanggotaan Gauss Suatu fungsi keanggotaan himpunan kabur dengan dua buah parameter 𝑎, 𝑏 ∈ ℝ. disebut. fungsi. keanggotaan. Gauss,. 𝐺𝑎𝑢𝑠𝑠 (𝑥; 𝑎, 𝑏), jika memenuhi: 𝐺𝑎𝑢𝑠𝑠 (𝑥; 𝑎, 𝑏) =. 𝑥−𝑎 2 −( 𝑒 𝑏 ). dinyatakan. dengan.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 13. dimana 𝑥 = 𝑎 adalah pusat dan b menentukan lebar dari grafik fungsi keanggotaan Gauss tersebut. Contoh 2.2.3 Misalkan diketahui fungsi keanggotaan Gauss (x; 15, 15), maka grafik fungsi keanggotaan tersebut adalah. Gambar 2.3 Fungsi Keanggotaan Gauss (𝑥; 15, 15) 4. Fungsi Keanggotaan Cauchy Suatu fungsi keanggotaan himpunan kabur dengan tiga buah parameter a, b, c ∈ ℝ disebut fungsi keanggotaan Cauchy atau fungsi keanggotaan genta, dinyatakan dengan Cauchy (x; a, b, c), jika memenuhi: 𝐶𝑎𝑢𝑐ℎ𝑦 (𝑥; 𝑎, 𝑏, 𝑐 ) =. 1 𝑥 − 𝑐 2𝑏 1+ | 𝑎 |. dimana x = c adalah pusat, a menentukan lebar, dan b menentukan kemiringan (slope) di titik silang dari fungsi keanggotaan Cauchy tersebut.. Contoh 2.2.4 Misalkan diketahui fungsi keanggotaan Cauchy (x; 8, 2, 15), maka grafik fungsi keanggotaan tersebut adalah.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 14. Gambar 2.4 Fungsi Keanggotaan Cauchy (𝑥; 8, 2, 15) 5. Fungsi Keanggotaan Sigmoid Suatu fungsi keanggotaan himpunan kabur dengan dua buah parameter a dan c ∈ ℝ disebut fungsi keanggotaan sigmoid, dinyatakan dengan Sigmoid (x; a, c), jika memenuhi: 𝑆𝑖𝑔𝑚𝑜𝑖𝑑 (𝑥; 𝑎, 𝑐 ) =. 1 1 + 𝑒 −𝑎(𝑥−𝑐). dimana a menentukan kemiringan fungsi sigmoid tersebut di titik silang x = c. Jika 𝑎 > 0 maka grafik terbuka kanan dan jika 𝑎 < 0 maka grafik terbuka kiri. Contoh 2.2.5 Misalkan diketahui fungsi keanggotaa Sigmoid (x; 3, 6), maka grafik fungsi keanggotaan tersebut adalah. Gambar 2.5 Fungsi Keanggoaan Sigmoid (𝑥; 3, 6) yang Terbuka Kanan.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 15. Contoh 2.2.6 Misalkan diketahui fungsi keanggotaan Sigmoid (x; −3, 6), maka grafik fungsi keanggotaan tersebut adalah. Gambar 2.6 Fungsi Keanggoaan Sigmoid (𝑥; −3, 6) yang Terbuka Kiri C. Operasi-Operasi pada Himpunan Kabur Sama seperti pada himpunan tegas, dalam himpunan kabur juga dapat didefinisikan operasi uner “komplemen” dan operasi-operasi biner “gabungan” dan “irisan”. Suatu himpunan tegas dapat dinyatakan secara lengkap dengan fungsi karakteristiknya sehingga ketiga operasi pada himpunan tegas itu dapat didefinisikan dengan menggunakan fungsi karakteristik itu. Ketiga operasi tersebut adalah sebagai berikut: 1. Komplemen Misalnya A adalah suatu himpunan tegas dalam semesta X, maka komplemen dari A, yaitu 𝐴′, dapat didefinisikan dengan tabel nilai kebenaran sebagai berikut: 𝑥∈𝐴 1 0. 𝑥 ∈ 𝐴′ 0 1.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 16. Bila 𝜒𝐴 adalah fungsi karakteristik dari himpunan A tersebut, maka definisi komplemen itu juga dapat dinyatakan dengan menggunakan fungsi karakteristik sebagai berikut 𝜒𝐴′ (𝑥 ) = 1 − 𝜒𝐴 (𝑥), ∀𝑥 ∈ 𝑋. 2. Gabungan Gabungan dari himpunan-himpunan tegas A dan B dalam semesta X, yaitu A ∪ 𝐵, dapat didefinisikan dengan menggunakan tabel kebenaran sebagai berikut: 𝑥∈𝐴 1 1 0 0. 𝑥∈𝐵 1 0 1 0. 𝑥 ∈𝐴∪𝐵 1 1 1 0. Definisi tersebut juga dapat dinyatakan dengan menggunakan fungsi karakteristik sebagai berikut 𝜒𝐴∪𝐵 (𝑥 ) = max{𝜒𝐴 (𝑥 ), 𝜒𝐵 (𝑥 )} , ∀𝑥 ∈ 𝑋. 3. Irisan Irisan dari himpunan-himpunan tegas A dan B dalam semesta X, yaitu dinotasikan A ∩ 𝐵, dapat didefinisikan dengan menggunakan tabel kebenaran sebagai berikut: 𝑥∈𝐴 1 1 0 0. 𝑥∈𝐵 1 0 1 0. 𝑥 ∈𝐴∩𝐵 1 0 0 0. Definisi tersebut juga dapat dinyatakan dengan menggunakan fungsi karakteristik sebagai berikut 𝜒𝐴∩𝐵 (𝑥 ) = min{𝜒𝐴 (𝑥), 𝜒𝐵 (𝑥 )} , ∀𝑥 ∈ 𝑋..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 17. Karena fungsi keanggotaan suatu himpunan kabur adalah perampatan dari fungsi karakteristik himpunan tegas, maka operasi-operasi pada himpunan kabur dapat didefinisikan sesuai dengan operasi-operasi pada himpunan tegas seperti didefinisikan di atas. 1. Komplemen Komplemen dari suatu himpunan kabur 𝐴̃ dalam semesta X adalah ̃ dengan fungsi keanggotaan himpunan kabur 𝐴′ 𝜇𝐴̃′ (𝑥 ) = 1 − 𝜇𝐴̃ (𝑥), ∀𝑥 ∈ 𝑋. 2. Gabungan Gabungan dua buah himpunan kabur 𝐴̃ dan 𝐵̃ dalam semesta X adalah himpunan kabur 𝐴̃ ∪ 𝐵̃ dengan fungsi keanggotaan 𝜇𝐴̃∪𝐵̃ (𝑥 ) = max{ 𝜇𝐴̃ (𝑥 ), 𝜇𝐵̃ (𝑥 )}, ∀𝑥 ∈ 𝑋. 3. Irisan Irisan dua buah himpunan kabur 𝐴̃ dan 𝐵̃ dalam semesta X adalah himpunan kabur 𝐴̃ ∩ 𝐵̃ dengan fungsi keanggotaan 𝜇𝐴̃∩𝐵̃ (𝑥 ) = min{ 𝜇𝐴̃ (𝑥 ), 𝜇𝐵̃ (𝑥 )}, ∀𝑥 ∈ 𝑋. Ketiga operasi yang didefinisikan di atas tersebut disebut operasi baku pada himpunan kabur. Contoh 2.3.1 Misalkan dalam semesta 𝑋 = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} diketahui himpunanhimpunan kabur 𝐴̃ = 0.1/1 + 0.5/2 + 0.7/3 + 0.8/4 + 0.9/5 + 0.8/6 + 0.5/7 + 0.3/8 + 0.2/9 + 0.1/10 𝐵̃ = 0.2/1 + 0.5/2 + 0.6/3 + 0.8/4 + 0.8/5 + 0.7/6 + 0.5/7 + 0.4/8 + 0.3/9 + 0.2/10 maka 𝐴̃ ′. = 0.9/1 + 0.5/2 + 0.3/3 + 0.2/4 + 0.1/5 + 0.2/6 + 0.5/7 + 0.7/8 + 0.8/9 + 0.9/10.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 18. 𝐵̃ ′. = 0.8/1 + 0.5/2 + 0.4/3 + 0.2/4 + 0.2/5 + 0.3/6 + 0.5/7 + 0.6/8 + 0.7/9 + 0.8/10. 𝐴̃ ∪ 𝐵̃ = 0.2/1 + 0.5/2 + 0.7/3 + 0.8/4 + 0.9/5 + 0.8/6 + 0.5/7 + 0.4/8 + 0.3/9 + 0.2/10 𝐴̃ ∩ 𝐵̃ = 0.1/1 + 0.5/2 + 0.6/3 + 0.8/4 + 0.8/5 + 0.7/6 + 0.5/7 + 0.3/8 + 0.2/9 + 0.1/10 Seperti halnya pada himpunan tegas, pada himpunan kabur juga berlaku sifatsifat operasi sebagai berikut: 1.. ′ (𝐴̃ ′ ) = 𝐴̃. (Involusi). 2.. 𝐴̃ ∪ 𝐴̃ = 𝐴̃ dan 𝐴̃ ∩ 𝐴̃ = 𝐴̃. (Idempoten). 3.. 𝐴̃ ∪ ∅ = 𝐴̃ dan 𝐴̃ ∪ 𝑋 = 𝐴̃. (Identitas). 4.. 𝐴̃ ∪ 𝐵̃ = 𝐵̃ ∪ 𝐴̃ dan 𝐴̃ ∩ 𝐵̃ = 𝐵̃ ∩ 𝐴̃. (Komutatif). 5.. 𝐴̃ ∪ ( 𝐵̃ ∪ 𝐶̃ ) = (𝐴̃ ∪ 𝐵̃ ) ∪ 𝐶̃ 𝐴̃ ∩ ( 𝐵̃ ∩ 𝐶̃ ) = (𝐴̃ ∩ 𝐵̃ ) ∩ 𝐶̃. 6.. 7. 8.. (Asosiatif). 𝐴̃ ∪ ( 𝐵̃ ∩ 𝐶̃ ) = (𝐴̃ ∪ 𝐵̃ ) ∩ (𝐴̃ ∪ 𝐶̃ ) 𝐴̃ ∩ ( 𝐵̃ ∪ 𝐶̃ ) = (𝐴̃ ∩ 𝐵̃ ) ∪ (𝐴̃ ∩ 𝐶̃ ). (Distributif). 𝐴̃ ∪ (𝐴̃ ∩ 𝐵̃ ) = 𝐴̃ dan 𝐴̃ ∩ (𝐴̃ ∪ 𝐵̃ ) = 𝐴̃. (Absorbsi). ′ ′ (𝐴̃ ∪ 𝐵̃ ) = 𝐴̃ ′ ∩ 𝐵̃ ′ dan (𝐴̃ ∩ 𝐵̃ ) = 𝐴̃ ′ ∪ 𝐵̃ ′. (De Morgan). Operasi-operasi komplemen, gabungan, dan irisan yang didefinisikan di atas disebut operasi baku untuk himpunan-himpunan kabur. Definisi tersebut dapat dirampatkan sedemikian sehingga definisi operasi-operasi baku tersebut merupakan kejadian khususnya. Perampatan tersebut akan didefinisikan dengan menggunakan sifat-sifat yang harus dipenuhi, kemudian akan diperlihatkan macammacam operasi yang memenuhi sifat-sifat tersebut. Definisi 2.3.1 Komplemen Kabur Suatu pemetaan 𝑘: [0,1] → [0,1] disebut komplemen kabur jika memenuhi sifatsifat berikut:.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 19. K1.. k(0) = 1 dan k(1) = 0 (syarat batas).. K2.. Jika x ≤ y, maka k(x) ≥ k(y) untuk semua 𝑥, 𝑦 ∈ [0,1] (syarat taknaik).. Contoh 2.3.2 Operasi komplemen baku, yaitu 𝑘(𝑥 ) = 1 − 𝑥. Kelas Sugeno yang didefinisikan sebagai berikut: 𝑘𝜆 (𝑥 ) =. 1−𝑥 1 + 𝜆𝑥. dengan prameter 𝜆 = (−1, ∞). Untuk setiap nilai parameter 𝜆 diperoleh operasi komplemen kabur. Untuk 𝜆 = 0, diperoleh operasi komplemen baku, yaitu 𝑘0 (𝑥 ) = 1 − 𝑥, dimana x adalah derajat keanggotaan suatu elemen dalam suatu himpunan kabur 𝐴̃ dan 𝑘0 (𝑥 ) adalah derajat keanggotaan elemen tersebut dalam ̃. himpunan kabur 𝐴′ Contoh 2.3.3 Kelas Yager yang didefinisikan sebagai berikut: 𝑘𝑤 (𝑥 ) = (1 − 𝑥 𝑤 )1/𝑤 dengan parameter 𝑤 ∈ (0, ∞). Untuk setiap nilai parameter w diperoleh suatu himpunan kabur, dan untuk w = 1, diperoleh operasi komplemen baku, yaitu 𝑘1 (𝑥 ) = 1 − 𝑥. Definisi 2.3.2 Gabungan Kabur: Norma-s Suatu pemetaan 𝑠 ∶ [0,1] × [0,1] → [0,1] disebut gabungan kabur (norma-s) jika untuk setiap 𝑥, 𝑦, 𝑧 ∈ [0, 1] memenuhi sifat-sifat berikut: S1.. 𝑠(0, 𝑥 ) = 𝑠 (𝑥, 0) = 𝑥 dan 𝑠(1,1) = 1. S2.. 𝑠(𝑥, 𝑦) = 𝑠 (𝑦, 𝑥 ). (syarat komutatif). (syarat batas).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 20. S3.. Jika 𝑥 ≤ 𝑥′ dan 𝑦 ≤ 𝑦′, maka 𝑠(𝑥, 𝑦) ≤ 𝑠(𝑥′, 𝑦′) untuk semua 𝑥, 𝑦 ∈ [0,1] (syarat takturun). S4.. 𝑠(𝑠(𝑥, 𝑦), 𝑧) = 𝑠(𝑥, 𝑠(𝑦, 𝑧)) (syarat asosiatif). Contoh 2.3.4 Contoh-contoh norma-s adalah sebagai berikut: a. Gabungan baku : 𝑠(𝑥, 𝑦) = max{𝑥, 𝑦} b. Jumlah aljabar. : 𝑠𝑗𝑎 (𝑥, 𝑦) = 𝑥 + 𝑦 − 𝑥𝑦. c. Jumlah Eistein. :. 𝑠𝑗𝑒 (𝑥, 𝑦) =. d. Jumlah drastis. 𝑥+𝑦 1 + 𝑥𝑦.  x jika 𝑦 = 0 … .  : 𝑠𝑗𝑑 (𝑥, 𝑦) =  y jika 𝑥 = 0 … .  1 jika 𝑥 lainnya . Beberapa kelas pemetaan yang merupakan norma-s (gabungan kabur), yaitu: a. Kelas Yager 𝑠𝑤 (𝑥, 𝑦) = min{1, (𝑥 𝑤 + 𝑦 𝑤 )1/𝑤 } , 𝑤 ∈ (0, ∞) b. Kelas Dubois-Prade 𝑠𝛼 (𝑥, 𝑦) =. 𝑥 + 𝑦 − 𝑥𝑦 − min {𝑥, 𝑦, 1 − 𝛼 } , 𝛼 ∈ [0,1] max {1 − 𝑥, 1 − 𝑦, 𝛼 }. c. Kelas Dombi 𝑠𝜆 (𝑥, 𝑦) =. 1 1 1 + ((𝑥 − 1). −𝜆. −𝜆 −1/𝜆. 1 + (𝑦 − 1) ). , 𝜆 ∈ (0, ∞).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 21. Teorema 2.3.3 Untuk setiap operasi gabungan kabur s dan setiap 𝑥, 𝑦 ∈ [0, 1] berlaku max{𝑥, 𝑦} ≤ 𝑠(𝑥, 𝑦) ≤ 𝑠𝑗𝑑 (𝑥, 𝑦). Bukti: Ambil sebarang operasi gabungan kabur s dan sebarang 𝑥, 𝑦 ∈ [0, 1]. Karena s memenuhi syarat batas dan syarat takturun dari norma-s, maka diperoleh 𝑠(𝑥, 0) = 𝑥 dan 𝑠(0, 𝑦) = 𝑦.. (syarat batas). Karena 0 ≤ 𝑥, maka 𝑠(0, 𝑦) ≤ 𝑠(𝑥, 𝑦).. (syarat takturun). Karena 0 ≤ 𝑦, maka 𝑠(𝑥, 0) ≤ 𝑠(𝑥, 𝑦).. (syarat takturun). Jadi,. 𝑠(𝑥, 𝑦) ≥ 𝑠 (0, 𝑦) = 𝑦, sehingga 𝑦 ≤ 𝑠(𝑥, 𝑦) 𝑠(𝑥, 𝑦) ≥ 𝑠 (𝑥, 0) = 𝑥, sehinngga 𝑥 ≤ 𝑠(𝑥, 𝑦).. Maka diperoleh max{𝑥, 𝑦} ≤ 𝑠(𝑥, 𝑦). Selanjutnya, jika 𝑥 = 0, maka 𝑠(𝑥, 𝑦) = 𝑠(0, 𝑦) = 𝑦 = 𝑠𝑗𝑑 (𝑥, 𝑦) jika 𝑦 = 0, maka 𝑠(𝑥, 𝑦) = 𝑠(𝑥, 0) = 𝑥 = 𝑠𝑗𝑑 (𝑥, 𝑦) jika 𝑥 ≠ 0 dan 𝑦 ≠ 0, maka 𝑠(𝑥, 𝑦) ≤ 1 = 𝑠𝑗𝑑 (𝑥, 𝑦) Terbukti bahwa 𝑠(𝑥, 𝑦) ≤ 𝑠𝑗𝑑 (𝑥, 𝑦). ∎ Definisi 2.3.4 Irisan Kabur: (Norma-t) Suatu pemetaan 𝑡 ∶ [0,1] × [0,1] → [0,1] disebut irisan kabur (norma-t) jika untuk setiap 𝑥, 𝑦, 𝑧 ∈ [0, 1] memenuhi sifat-sifat berikut: T1.. 𝑡(𝑥, 1) = 𝑡(1, 𝑥 ) = 𝑥 dan 𝑡(0,0) = 0. (syarat batas).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 22. T2.. 𝑡(𝑥, 𝑦) = 𝑡(𝑦, 𝑥 ). T3.. Jika 𝑥 ≤ 𝑥′ dan 𝑦 ≤ 𝑦′, maka 𝑡(𝑥, 𝑦) ≤ 𝑡(𝑥′, 𝑦′) untuk semua 𝑥, 𝑦 ∈ [0,1]. (syarat komutatif). (syarat takturun) T4.. 𝑡(𝑡(𝑥, 𝑦), 𝑧) = 𝑡(𝑥, 𝑡(𝑦, 𝑧)) (syarat asosiatif). Contoh 2.3.5 Contoh-contoh suatu norma-t adalah sebagai berikut: a. Irisan baku. : 𝑡(𝑥, 𝑦) = min{𝑥, 𝑦}. b. Darab aljabar. : 𝑡𝑑𝑎 (𝑥, 𝑦) = 𝑥𝑦. c. Darab Eistein. : 𝑡𝑑𝑒 (𝑥, 𝑦) =. d. Darab drastis. 𝑥𝑦 2 − (𝑥 + 𝑦 − 𝑥𝑦).  x jika 𝑦 = 1 … .  : 𝑡𝑑𝑑 (𝑥, 𝑦) =  y jika 𝑥 = 1 … .  0 jika 𝑥 lainnya . Beberapa kelas pemetaan yang merupakan norma-t (irisan kabur), yaitu: a. Kelas Yager 1. 𝑡𝑤 (𝑥, 𝑦) = 1 − min {1 − ((1 − 𝑥 )𝑤 + (1 − 𝑦)𝑤 )𝑤 } , 𝑤 ∈ (0, ∞) b. Kelas Dubois-Prade 𝑡𝛼 (𝑥, 𝑦) =. 𝑥𝑦 , 𝛼 ∈ [0,1] max{𝑥, 𝑦, 𝛼 }. c. Kelas Dombi 𝑡𝜆 (𝑥, 𝑦) =. 1 𝜆. 𝜆 1/𝜆. 1 1 1 + ((𝑥 − 1) + (𝑦 − 1) ). , 𝜆 ∈ (0, ∞).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 23. Teorema 2.3.5 Untuk setiap operasi irisan kabur t dan setiap 𝑥, 𝑦 ∈ [0, 1] berlaku 𝑡𝑑𝑑 (𝑥, 𝑦) ≤ 𝑡(𝑥, 𝑦) ≤ min{𝑥, 𝑦}. Bukti: Ambil sebarang operasi irisan kabur t dan sebarang 𝑥, 𝑦 ∈ [0, 1]. Karena t memenuhi syarat batas dan syarat takturun dari norma-t, maka diperoleh 𝑡(𝑥, 1) = 𝑥 dan 𝑡(1, 𝑦) = 𝑦.. (syarat batas). Karena 𝑥 ≤ 1, maka 𝑡(𝑥, 𝑦) ≤ 𝑡(1, 𝑦).. (syarat takturun). Karena 𝑦 ≤ 1, maka 𝑡(𝑥, 𝑦) ≤ 𝑡(𝑥, 1).. (syarat takturun). Jadi, 𝑡(𝑥, 𝑦) ≤ 𝑡(𝑥, 1) = 𝑥, sehingga 𝑡(𝑥, 𝑦) ≤ 𝑥 𝑡(𝑥, 𝑦) ≤ 𝑡(1, 𝑦) = 𝑦, sehingga 𝑡(𝑥, 𝑦) ≤ 𝑦. Maka diperoleh 𝑡(𝑥, 𝑦) ≤ min{𝑥, 𝑦}. Selanjutnya, jika 𝑥 = 1, maka 𝑡(𝑥, 𝑦) = 𝑡(1, 𝑦) = 𝑦 = 𝑡𝑑𝑑 (𝑥, 𝑦) jika 𝑦 = 1, maka 𝑡(𝑥, 𝑦) = 𝑡(𝑥, 1) = 𝑥 = 𝑡𝑑𝑑 (𝑥, 𝑦) jika 𝑥 ≠ 1 dan 𝑦 ≠ 1, maka berlaku 𝑡𝑑𝑑 (𝑥, 𝑦) = 0 ≤ 𝑡(𝑥, 𝑦) Terbukti bahwa 𝑡𝑑𝑑 (𝑥, 𝑦) ≤ 𝑡(𝑥, 𝑦). ∎ D. Relasi Kabur Definisi 2.4.1 Relasi kabur 𝑅̃ antara elemen-elemen dalam himpunan X dengan elemen-elemen dalam himpunan Y didefinisikan sebagai himpunan bagian kabur dari darab Cartesisus 𝑋 × 𝑌, yaitu himpunan kabur.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 24. 𝑅̃ = {((𝑥, 𝑦), 𝜇𝑅̃ (𝑥, 𝑦))│(𝑥, 𝑦) ∈ 𝑋 × 𝑌}. Jika himpunan X dan Y keduanya berhingga, misalnya 𝑋 = {𝑥1 , 𝑥2 , ⋯ , 𝑥𝑚 } dan 𝑌 = {𝑦1 , 𝑦2 , ⋯ , 𝑦𝑛 }, maka relasi kabur 𝑅̃ antara elemen-elemen dalam himpunan X dengan elemen-elemen dalam himpunan Y dapat dinyatakan dalam bentuk suatu matriks berukuran 𝑚 × 𝑛 sebagai berikut: 𝑎11 𝑅̃ = [ 𝑎21 ⋮ 𝑎𝑚1. 𝑎12 ⋯ 𝑎22 ⋯ ⋮. 𝑎𝑚2 ⋯. 𝑎1𝑛 𝑎2𝑛 ] ⋮ 𝑎𝑚𝑛. dimana 𝑎𝑖𝑗 = 𝜇𝑅̃ (𝑥𝑖 , 𝑦𝑗 ) untuk 𝑖 = 1,2, ⋯ , 𝑚 dan 𝑗 = 1,2, ⋯ , 𝑛. Bila X=Y, maka relasi kabur 𝑅̃ pada himpunan X itu dapat disajikan dengan suatu matriks persegi. Contoh 2.4.1 Misalkan 𝑋 = {1, 27, 119}, 𝑌 = {10, 225, 94}, dan 𝑅̃ adalah relasi kabur “jauh lebih kecil” antara elemen-elemen dalam X dengan elemen-elemen dalam Y. Maka relasi 𝑅̃ tersebut dapat dinyatakan sebagai 𝑅̃ = 0.1/(1, 10) + 0.9/(1, 225) + 0.5/(1, 94) + 0.8/(27, 225) + 0.3/(27, 94) + 0.5/(119, 225). Relasi 𝑅̃ tersebut dapat juga dinyatakan dalam bentuk matriks persegi sebagai berikut: 0.1 0.9 0.5 ̃ [ 𝑅 = 0.0 0.8 0.3] 0.0 0.5 0.0 dengan elemen baris ke-i kolom ke-j dalam matriks tersebut menyatakan derajat keanggotaan (𝑥𝑖 , 𝑦𝑗 ) dalam relasi 𝑅̃ , yaitu 𝜇𝑅̃ (𝑥𝑖 , 𝑦𝑗 ), dimana 𝑥𝑖 ∈ 𝑋 dan 𝑦𝑗 ∈ 𝑌. Definisi 4.2.4 Invers dari suatu relasi kabur 𝑅̃ pada semesta 𝑋 × 𝑌, yang dinyatakan dengan 𝑅̃ −1 , adalah relasi kabur pada semesta 𝑌 × 𝑋 dengan fungsi keanggotaan 𝜇𝑅̃ −1 (𝑦, 𝑥 ) = 𝜇𝑅̃ (𝑥, 𝑦) untuk setiap (𝑦, 𝑥 ) ∈ 𝑌 × 𝑋. Jelas bahawa (𝑅̃ −1 ). −1. = 𝑅̃ untuk setiap relasi kabur. 𝑅̃ . Matriks dari invers dari relasi kabur 𝑅̃ , yaitu 𝑅̃ −1 , adalah transpos dari matriks dari relasi 𝑅̃ ..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 25. Contoh 2.4.2 0.1 Dari contoh 2.4.1 diperoleh 𝑅̃ −1 = [0.9 0.5. 0.0 0.8 0.3. 0.0 0.5]. 0.0.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI. BAB III LOGIKA KABUR. A. Variabel Linguistik Suatu variabel adalah suatu lambang atau kata yang menunjuk kepada sesuatu yang tidak tertentu dalam semesta wacananya. Misalnya dalam kalimat: “Mahasiswa itu lulus dengan pujian”, kata “mahasiswa” adalah suatu variabel karena menunjuk kepada orang yang tidak tertentu dalam semesta wacananya yaitu himpunan manusia. Demikian pula dalam kalimat: “y habis dibagi 3”, lambang “y" adalah suatu variabel dengan semesta wacana himpunan bilangan-bilangan. Suatu variabel dapat diganti oleh unsur-unsur dalam semesta wacananya, misalnya variabel “mahasiswa” dapat diganti dengan “Budi” dan variabel “y” dapat diganti dengan bilangan 6. Kata “Budi” dan lambang “6” menunjuk pada unsur yang tertentu pada masing-masing semesta wacananya, dan disebut konstanta. Terdapat dua jenis variabel, yaitu: 1. Variabel numeris, yang digunakan bila semesta wacananya adalah himpunan bilangan-bilangan. 2. Variabel linguistik, yang digunakan bila semesta wacananya adalah himpunan kata-kata atau istilah-istilah dari bahasa sehari-hari. Suatu variabel linguistik adalah suatu rangkap-5 (x, T, X, G, M) dimana: a. x adalah lambang variabelnya. b. T adalah himpunan nilai-nilai linguistik yang dapat menggantikan x. c. X adalah semesta wacana (numeris) dari nilai-nilai linguistik dalam T. d. G adalah himpunan aturan-aturan sintaksis yang mengatur pembentukan istilah-istilah anggota T. e. M adalah himpunan aturan-aturan semantik yang mengaitkan setiap istilah T dengan suatu himpunan kabur dalam semesta wacana X.. 26.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 27. Contoh 3.1.1 Bila variabel linguistiknya adalah “kecepatan”, maka sebagai himpunan nilai-nilai linguistik dapat diambil himpunan istilah-istilah 𝑇 = {sangat lambat, lambat, agak lambat, cepat, agak cepat, sangat cepat}, dengan semesta numeris 𝑋 = [0, 160], himpunan aturan sintaksis 𝐺 = {𝑥│𝑥 = aturan pembentukan kata majemuk yang mengikuti kaidah yang berlaku dalam bahasa Indonesia}, 160−𝑥 160. dan. himpunan. aturan. semantik. 𝑀 = {𝜇𝑙𝑎𝑚𝑏𝑎𝑡 (𝑥 ) =. 𝑥. , 𝜇𝑐𝑒𝑝𝑎𝑡 (𝑥) = 160 , 𝜇𝑠𝑎𝑛𝑔𝑎𝑡𝐴 (𝑥 ) = (𝜇𝐴̃ (𝑥))2 , 𝜇𝑎𝑔𝑎𝑘𝐴 (𝑥 ) = √𝜇𝐴̃ (𝑥)}.. B. Pengubah Linguistik Pengubah lingusitik adalah suatu kata yang dipergunakan untuk mengubah suatu kata/istilah menjadi suatu kata/istilah yang baru dengan makna yang baru. Dua buah pengubah linguistik yang paling sering digunakan adalah “sangat” dan “agak”. Jika suatu istilah A dikaitkan dengan himpunan kabur 𝐴̃ dalam semesta X, maka istilah “sangat A” dikaitkan dengan himpunan kabur konsentrasi dari 𝐴̃ dengan lambang Kon(𝐴̃) dan fungsi keanggotaan 𝜇𝐾𝑜𝑛(𝐴̃) (𝑥 ) = (𝜇𝐴̃ (𝑥))2 , ∀ 𝑥 ∈ 𝑋 sedangkan istilah “agak A” dikaitkan dengan himpunan kabur dilasi dari 𝐴̃ dengan lambang Dil(𝐴̃) dan fungsi keanggotaan 𝜇𝐷𝑖𝑙(𝐴̃) (𝑥 ) = (𝜇𝐴̃ (𝑥))1/2 , ∀ 𝑥 ∈ 𝑋. Contoh 3.2.1 Misalkan 𝑋 = {6, 7, 8, 9, 10} dan istilah “dekat dengan 10” dikaitkan dengan himpunan kabur 𝐴̃ = 0.60/6 + 0.70/7 + 0.80/8 + 0.90/9 + 1.00/10. Maka istilah.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 28. “sangat dekat dengan 10” dikaitkan dengan himpunan kabur 𝐾𝑜𝑛(𝐴̃) = 0.36/6 + 0.49/7 + 0.64/8 + 0.81/9 + 1.00/10 “sangat dekat sekali dengan 10” dikaitkan dengan himpunan kabur 𝐾𝑜𝑛(𝐾𝑜𝑛(𝐴̃)) = 0.1296/6 + 0.2401/7 + 0.4096/8 + 0.6561/9 + 1.00/10 “agak dekat dengan 10” dikaitkan dengan himpunan kabur 𝐷𝑖𝑙(𝐴̃) = 0.77/6 + 0.84/7 + 0.89/8 + 0.95/9 + 1.00/10 “tidak sangat dekat dengan 10” dikaitkan dengan himpunan kabur (𝐾𝑜𝑛(𝐴̃))′ = 0.64/6 + 0.51/7 + 0.36/8 + 0.19/9 “dekat tetapi tidak sangat dekat dengan 10” dikaitkan dengan himpunan kabur 𝐴̃ ∩ (𝐾𝑜𝑛(𝐴̃))′ = 0.60/6 + 0.51/7 + 0.36/8 + 0.19/9. C. Proposisi Kabur Proposisi kabur adalah kalimat yang memuat predikat kabur, yaitu predikat yang dapat direpresentasikan dengan suatu himpunan kabur. Proposisi kabur yang mempunyai nilai kebenaran tertentu disebut pernyataan kabur. Nilai kebenaran dari suatu pernyataan kabur disajikan dengan suatu bilangan real dalam selang [0,1]. Nilai kebenaran itu disebut derajat kebenaran dari pernyaataan kabur itu. Bentuk umum dari proposisi kabur adalah 𝑥 adalah 𝐴 dimana x adalah suatu variabel linguistik dan predikat A adalah suatu nilai linguistik dari x. Bila 𝐴̃ adalah himpunan kabur yang dikaitkan dengan nilai linguistik A dan 𝑥0 adalah suatu elemen tertentu dalam semesta X dari himpunan kabur 𝐴̃ , maka 𝑥0 mempunyai derajat keanggotaan 𝜇𝐴̃ (𝑥0 ) dalam himpunan kabur 𝐴̃ . Derajat kebenaran dari pernyataan kabur 𝑥0 adalah 𝐴.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 29. didefinisikan sama dengan derajat keanggotaan 𝑥0 dalam himpunan kabur 𝐴̃ , yaitu 𝜇𝐴̃ (𝑥0 ). Misalkan proposisi kabur “𝑥 adalah 𝐴” dilambangkan dengan 𝑝(𝑥), pernyataan kabur “𝑥0 adalah 𝐴” dengan 𝑝(𝑥0 ), dan derajat keanggotaan dari 𝑝(𝑥0 ) dengan 𝜏(𝑝(𝑥0 )), maka 𝜏(𝑝(𝑥0 )) = 𝜇𝐴̃ (𝑥0 ) . Seperti halnya dengan proposisi yang tegas, kita juga dapat membentuk proposisi kabur majemuk dari proposisi-proposisi kabur tunggal, dengan mengunakan operator-operator logika. Beberapa contoh proposisi kabur majemuk misalnya: Orang itu kaya dan rumahnya besar Sekolah itu mahal atau kemampuan finansial orangtua siswanya rendah Bila prestasi studi tinggi, maka peluang memperoleh beasiswa juga tinggi Udara dingin bila dan hanya bila suhunya rendah Secara umum terdapat empat macam proposisi kabur majemuk dengan operator logika biner, yaitu: Konjungsi kabur. : x adalah A dan y adalah B. Disjungsi kabur. : x adalah A atau y adalah B. Implikasi kabur. : Bila x adalah A, maka y adalah B. Ekivalensi kabur. : x adalah A bila dan hanya bila y adalah B. Variabel-variabel linguistik dalam proposisi-proposisi tunggal penyusunnya tidak harus sama (yaitu tidak harus dalam semesta numeris yang sama). Misalkan x adalah variabel linguistik dengan semesta numeris X, dan A adalah suatu predikat kabur yang dikaitkan dengan himpunan kabur 𝐴̃ dalam X, maka negasi dari proposisi kabur “x adalah A” adalah proposisi kabur x adalah tidak A dengan predikat kabur “tidak A” yang dapat dikaitkan dengan himpunan kabur komplemen kabur dari 𝐴̃ , yaitu 𝐴̃ ′, dengan fungsi keanggotaan 𝜇𝐴̃′ (𝑥 ) = 𝑘(𝜇𝐴̃ (𝑥 )) dimana k adalah suatu komplemen kabur..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 30. Jika x adalah variabel linguistik dengan semesta numeris X dan y adalah variabel linguistik dengan semesta numeris Y , maka konjungsi kabur: x adalah A dan y adalah B di mana A dikaitkan dengan hipunan kabur 𝐴̃ dalam X, dan B dikaitkan dengan himpunan kabur 𝐵̃ dalam Y, dapat dipandang sebagai suatu relasi kabur ∧ dalam 𝑋 × 𝑌 dengan fungsi keanggotaan 𝜇∧ (𝑥, 𝑦) = 𝑡(𝜇𝐴̃ (𝑥 ), 𝜇𝐵̃ (𝑦)) dengan t adalah suatu norma-t, sedangkan disjungsi kabur: x adalah A atau y adalah B dapat dipandang sebagai suatu relasi kabur ∨ dalam 𝑋 × 𝑌 dengan fungsi keanggotaan 𝜇∨ (𝑥, 𝑦) = 𝑠(𝜇𝐴̃ (𝑥 ), 𝜇𝐵̃ (𝑦)) dengan s adalah suatu norma-s Proposisi kabur majemuk yang paling sering dipakai dalam aplikasi teori kabur adalah implikasi kabur.. D. Implikasi Kabur Bentuk umum suatu implikasi kabur adalah Bila x adalah A, maka y adalah B dengan A dan B adalah predikat-predikat kabur yang dikaitkan dengan himpunanhimpunan kabur 𝐴̃ dan 𝐵̃ dalam semesta X dan Y berturut-turut. Seperti halnya dengan konjungsi dan disjungsi kabur, implikasi kabur juga dapat dipandang sebagai suatu relasi kabur dalam 𝑋 × 𝑌, yang dilambangkan dengan →. Dalam logika dwinilai, telah diketahui bahwa implikasi tegas 𝑝 ⟹ 𝑞 ekivalen dengan ¬𝑝 ∨ 𝑞. Berdasarkan ekivalensi tersebut, dengan mengganti proposisi p dan q berturut-turut dengan proposisi kabur “x adalah A” dan “y adalah B”, implikasi kabur tersebut di atas dapat diinterpretasikan sebagai relasi kabur → dalam 𝑋 × 𝑌 dengan fungsi keanggotaan 𝜇⟶ (𝑥, 𝑦) = s (𝑘(𝜇𝐴̃ (𝑥 )), 𝜇𝐵̃ (𝑦)).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 31. dengan s adalah suatu norma-s dan k adalah suatu komplemen kabur. Bila sebagai norma-s dan komplemen kabur diambil operasi-operasi gabungan dan komplemen baku, maka diperoleh 𝜇→𝑑𝑟 (𝑥, 𝑦) = max(1 − 𝜇𝐴̃ (𝑥 ), 𝜇𝐵̃ (𝑦)) yang seringkali disebut implikasi Dienes-Rescher. Karena implikasi tegas 𝑝 ⟹ 𝑞 juga ekivalen dengan (𝑝 ∧ 𝑞 ) ∨ ¬𝑝, maka implikasi kabur di atas juga dapat diinterpretasikan sebagai relasi kabur → dalam 𝑋 × 𝑌 dengan fungsi keanggotaan 𝜇⟶ (𝑥, 𝑦) = s (𝑡(𝜇𝐴̃ (𝑥 ), 𝜇𝐵̃ (𝑦)), 𝑘(𝜇𝐴̃ (𝑥 ))) dengan s adalah suatu norma-s, t adalah suatu norma-t, dan k adalah suatu komplemen kabur. Bila sebagai norma-s, norma-t, dan komplemen kabur diambil operasi-operasi gabungan, irisan, dan komplemen baku, maka diperoleh 𝜇→𝑧 (𝑥, 𝑦) = max(min(𝜇𝐴̃ (𝑥 ), 𝜇𝐵̃ (𝑦)),1 − 𝜇𝐴̃ (𝑥 )) yang seringkali disebut implikasi Zadeh. Dalam literatur masih banyak interpretasi lainnya untuk implikasi kabur. Salah satu implikasi kabur yang paling sering digunakan dalam aplikasi sistem kabur adalah implikasi Mamdani. Implikasi ini didasarkan pada asumsi bahwa implikasi kabur pada dasarnya bersifat lokal, dalam arti bahwa implikasi Jika x adalah A, maka y adalah B hanya berbicara mengenai keadaan dimana x adalah A dan y adalah B saja, dan tidak mengenai keadaan lainnya di luar itu. Berdasarkan asumsi tersebut, implikasi kabur dapat dipandang sebagai suatu konjungsi kabur, sehingga diperoleh 𝜇⟶ (𝑥, 𝑦) = 𝑡(𝜇𝐴̃ (𝑥 ), 𝜇𝐵̃ (𝑦)) yang disebut implikasi Mamdani. Bila sebagai norma-t diambil operasi baku “min”, maka diperoleh 𝜇→𝑚𝑚 (𝑥, 𝑦) = min(𝜇𝐴̃ (𝑥 ), 𝜇𝐵̃ (𝑦)).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 32. dan bila sebagai norma-t diambil operasi “darab aljabar”, maka diperoleh 𝜇→𝑚𝑑 (𝑥, 𝑦) = 𝜇𝐴̃ (𝑥 )𝜇𝐵̃ (𝑦). Implikasi kabur dapat diperluas menjadi implikasi dengan bentuk umum: Jika <𝑃𝐾1 >, maka <𝑃𝐾2 > dengan 𝑃𝐾1 dan 𝑃𝐾2 berturut-turut adalah proposisi kabur dalam semesta 𝑋1 × 𝑋2 × ⋯ × 𝑋𝑛 dan 𝑌1 × 𝑌2 × ⋯ × 𝑌𝑛 . Contoh 3.4.1 Misalkan diketahui semesta 𝑋 = {𝑎, 𝑏, 𝑐, 𝑑 } dan 𝑌 = {𝑝, 𝑞, 𝑟}, dan implikasi kabur Jika x tinggi, maka y kecil di mana predikat “tinggi” dan “kecil” berturut-turut dikaitkan dengan himpunan kabur 𝐴̃ = 0.2/𝑎 + 0.5/𝑏 + 0.7/𝑐 + 0.9/𝑑 dan 𝐵̃ = 0.4/𝑝 + 0.6/𝑞 + 0.8/𝑟. Maka diperoleh 1. Implikasi Dienes-Rescher →𝑑𝑟 = 0.8/(a, p) + 0.8/(a, q) + 0.8/(a, r) + 0.5/(b, p) + 0.6/(b, q) + 0.8/(b, r) + 0.4/(c, p) + 0.6/(c, q) + 0.8/(c, r) + 0.4/(d, p) + 0.6/(d, q) + 0.8/(d, r) 2.. Implikasi Zadeh →𝑧 = 0.8/(a, p) + 0.8/(a, q) + 0.8/(a, r) + 0.5/(b, p) + 0.5/(b, q) + 0.5/(b, r) + 0.4/(c, p) + 0.6/(c, q) + 0.7/(c, r) + 0.4/(d, p) + 0.6/(d, q) + 0.8/(d, r). 3.. Implikasi Mamdani →𝑚𝑚 = 0.2/(a, p) + 0.2/(a, q) + 0.2/(a, r) + 0.4/(b, p) + 0.5/(b, q) + 0.5/(b, r) + 0.4/(c, p) + 0.6/(c, q) + 0.7/(c, r) + 0.4/(d, p) + 0.6/(d, q) + 0.8/(d, r) →𝑚𝑑 = 0.08/(a, p) + 0.12/(a, q) + 0.16/(a, r) + 0.2/(b, p) + 0.3/(b, q) + 0.4/(b, r) + 0.28/(c, p) + 0.42/(c, q) + 0.56/(c, r) + 0.36/(d, p) + 0.56/(d, q) + 0.72/(d, r).. E. Penalaran Kabur Penalaran kabur (fuzzy reasoning), yang seringkali juga disebut penalaran hampiran (approximate reasoning), adalah suatu cara penarikan kesimpulan berdasarkan seperangkat implikasi kabur dan suatu fakta yang diketahui (yang.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 33. sering kali disebut premis). Penalaran (penarikan kesimpulan) dalam logika klasik didasarkan pada tautologi-tautologi, yaitu proposisi-proposisi yang selalu benar, tanpa tergantung pada nilai kebenaran proposisi-proposisi penyusunnya. Salah satu aturan penalaran yang paling sering digunakan adalah modus ponens, yang didasarkan pada tautologi: ((𝑝 ⟹ 𝑞 ) ∧ 𝑝) ⟹ 𝑞. Bentuk umum penalaran modus ponens adalah sebagai berikut: Premis 1 (Kaidah). : Bila x adalah A, maka y adalah B. Premis 2 (Fakta). : x adalah A. Kesimpulan. : y adalah B. Suatu contoh penalaran modus ponens misalnya adalah sebagai berikut: Premis 1. : Bila cuaca mendung, maka Lisa tidak menjemur pakaian. Premis 2. : Cuaca mendung. Kesimpulan. : Lisa tidak menjemur pakaian. Aturan penalaran tegas ini dapat dirampatkan menjadi aturan penalaran kabur dengan premis dan kesimpulannya adalah proposisi-proposisi kabur, misalnya: Premis 1. : Bila kain itu halus, maka harganya mahal.. Premis 2. : Kain itu agak halus.. Kesimpulan. : Kain itu harganya agak mahal.. Penalaran tersebut dapat dirumuskan secara umum dengan skema sebagai berikut: Premis 1 (Kaidah). : Bila x adalah A, maka y adalah B. Premis 2 (Fakta). : x adalah 𝐴′. Kesimpulan. : y adalah 𝐵′. Penalaran kabur dengan skema seperti di atas disebut modus ponens rampat (generalized modus ponens). Untuk memperoleh kesimpulan tersebut secara sah, digunakan suatu aturan penarikan kesimpulan yang disebut kaidah inferensi komposisional,. yang. mengomposisikan. menghasilkan kesimpulan.. relasi-relasi. pada. premis. untuk.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 34. Kaidah inferensi komposisional dalam modus ponens rampat diterapkan sebagai berikut: Premis 1. : Bila x adalah A, maka y adalah B (yang merupakan relasi/implikasi kabur → di X ×Y). Premis 2. : x adalah 𝐴′ ̃ dalam (yang didapat direpresentasikan dengan himpunan kabur 𝐴′ X). Kesimpulan. : y adalah 𝐵′ ̃ = 𝐴′ ̃ ∘→ dalam diperoleh dengan menentukan himpunan kabur 𝐵′ Y dengan fungsi keanggotaan 𝜇𝐵̃ ′ (𝑦) = sup 𝑡(𝜇𝐴̃′ (𝑥), 𝜇→ (𝑥, 𝑦)) 𝑥∈𝑋. dengan t adalah suatu norma-t. Bila 𝐴′ misalnya adalah predikat kabur “sangat A”, untuk norma-t diambil operasi baku “min”, dan untuk implikasi kabur dipakai implikasi Mamdani →𝑚𝑑 , maka kesimpulan “y adalah 𝐵′ ” di atas diperoleh dengan menentukan himpunan kabur 𝐵̃ ′ dengan fungsi keanggotaan 𝜇𝐵̃ ′ (𝑦) = sup min{(𝜇𝐴̃ (𝑥))2 , 𝜇𝐴̃ (𝑥)𝜇𝐵̃ (𝑦)}. 𝑥∈𝑋. ̃ = 𝐴̃ , maka Bila 𝐴̃ dan 𝐵̃ adalah himpunan-himpunan tegas dan 𝐴′ 𝜇𝐵̃ ′ (𝑦) = sup min{𝜇𝐴̃ (𝑥), 𝜇𝐴̃ (𝑥)𝜇𝐵̃ (𝑦)} 𝑥∈𝑋. = sup 𝜇𝐴̃ (𝑥)𝜇𝐵̃ (𝑦) 𝑥∈𝑋. = 𝜇𝐵̃ (𝑦) ̃ = 𝐵̃ , yang berarti dalam kasus ini aturan penalaran untuk setiap 𝑦 ∈ 𝑌. Jadi, 𝐵′ tersebut tidak lain daripada modus ponens tegas yang sudah dikenal dalam logika tradisional. Hal yang sama dapat diperoleh bila untuk implikasi kabur dipakai implikasi Mamdani →𝑚𝑚 . Bila 𝐴′ adalah predikat kabur yang dikaitkan dengan himpunan kabur 𝐴̃ ′ , untuk norma-t diambil operasi baku “min” , dan untuk implikasi kabur dipakai implikasi Mamdani →𝑚𝑚 , maka kesimpulan “y adalah 𝐵′” diatas dapat diperoleh ̃ dengan fungsi keanggotaan dengan menentukan himpunan kabur𝐵′.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 35. 𝜇𝐵̃ ′ (𝑦) = sup min{𝜇𝐴̃′ (𝑥 ), min(𝜇𝐴̃ (𝑥 ), 𝜇𝐵̃ (𝑦))} 𝑥∈𝑋. = sup min{𝜇𝐴̃′ (𝑥 ), 𝜇𝐴̃ (𝑥 ), 𝜇𝐵̃ (𝑦)} 𝑥∈𝑋. = min {sup min( 𝜇𝐴̃′ (𝑥 ), 𝜇𝐴̃ (𝑥 )), 𝜇𝐵̃ (𝑦)} 𝑥∈𝑋. = min{𝑤, 𝜇𝐵̃ (𝑦)} dengan 𝑤 = sup min{𝜇𝐴̃′ (𝑥 ), 𝜇𝐴̃ (𝑥 )} = sup( 𝐴̃ ′ ∩ 𝐴̃ ) yang menyatakan derajat 𝑥∈𝑋. 𝑥∈𝑋. keserasian (degree of compatibility) antara predikat 𝐴′ dengan A. Jadi untuk memperoleh himpunan kabur 𝐵̃ ′ tersebut, pertama-tama ditentukan derajat keserasian w, yaitu supremum dari irisan himpunan kabur 𝐴̃ ′ dan 𝐴̃ , dan kemudian 𝐵̃ ′ diperoleh sebagai irisan w dengan himpunan kabur 𝐵̃ . Modus ponens rampat dapat digeneralisasikan menjadi modus ponen rampat multikondisional, yang terdiri dari m buah premis kabur berupa kaidah, sebuah peremis kabur berupa fakta, dan sebuah kesimpulan. Skema umumnya adalah sebagai berikut: Premis 1. : Bila 𝑥1 adalah 𝐴11 dan ⋯ dan 𝑥𝑛 adalah 𝐴1𝑛 , maka y adalah 𝐵1. Premis 2. : Bila 𝑥1 adalah 𝐴21 dan ⋯ dan 𝑥𝑛 adalah 𝐴2𝑛 , maka y adalah 𝐵2. ⋮. ⋮. ⋮. Premis m. : Bila 𝑥1 adalah 𝐴𝑚1 dan ⋯ dan 𝑥𝑛 adalah 𝐴𝑚𝑛 , maka y adalah 𝐵𝑚. Fakta. : 𝑥1 adalah 𝐴′1 dan ⋯ dan 𝑥𝑛 adalah 𝐴′𝑛. Kesimpulan : y adalah 𝐵′ dengan 𝐴𝑖𝑗 dan 𝐴′𝑗 adalah predikat kabur yang dikaitkan dengan himpunan kabur 𝐴̃𝑖𝑗 dan 𝐴̃′𝑗 dalam semesta 𝑋𝑗 , dan 𝐵𝑖 adalah predikat kabur yang dikaitkan dengan himpunan kabur 𝐵̃𝑖 dalam semesta Y (𝑖 = 1, ⋯ , 𝑚; 𝑗 = 1, ⋯ , 𝑛). Masing-masing premis tersebut dapat dipandang sebagai suatu relasi kabur 𝑅̃𝑖 (𝑖 = 1, ⋯ , 𝑚) dalam ̃ = 𝐴̃′1 × ⋯ × 𝐴̃′𝑛 𝑋1 × ⋯ × 𝑋𝑛 × 𝑌 dan faktanya sebagai himpunan kabur 𝐴′ dalam 𝑋1 × ⋯ × 𝑋𝑛 . Premis-premis 𝑅̃𝑖 tersebut biasanya diperlakukan secara disjungtif, sehingga semua premis itu dapat digabung menjadi satu premis 𝑅̃, yaitu ̃ 𝑅̃ = ⋃𝑚 𝑖=1 𝑅𝑖 . Maka kesimpulan “𝑦 adalah 𝐵′” dapat diperoleh dengan kaidah inferensi komposisional untuk menentukan himpunan kabur 𝐵̃′ = 𝐴̃′ ∘ 𝑅̃ dalam.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 36. semesta Y dengan fungsi keanggotaan (dengan mengambil operasi baku “min” untuk norma-t dan “max” untuk gabungan kabur) 𝜇𝐵̃′ (𝑦) = 𝜇𝐴̃′∘𝑅̃ (𝑦) =. sup (𝑥1 ,⋯,𝑥𝑛 )∈𝑋1 ×⋯×𝑋𝑛. min{𝜇𝐴̃′ (𝑥1 , ⋯ , 𝑥𝑛 ), 𝜇𝑅̃ (𝑥1 , ⋯ , 𝑥𝑛 , 𝑦)}. = sup min {𝜇𝐴̃′ (𝑥1 , ⋯ , 𝑥𝑛 ), max (𝜇𝑅̃𝑖 (𝑥1 , ⋯ , 𝑥𝑛 , 𝑦))} 𝑖∈{1,⋯,𝑚}. 𝑥𝑗 ∈𝑋𝑗. = sup. max. 𝑥𝑗 ∈𝑋𝑗 𝑖∈{1,⋯,𝑚}. = max. min{𝜇𝐴̃′ (𝑥1 , ⋯ , 𝑥𝑛 ), 𝜇𝑅̃𝑖 (𝑥1 , ⋯ , 𝑥𝑛 , 𝑦)}. sup min{𝜇𝐴̃′ (𝑥1 , ⋯ , 𝑥𝑛 ), 𝜇𝑅̃𝑖 (𝑥1 , ⋯ , 𝑥𝑛 , 𝑦)}. 𝑖∈{1,⋯,𝑚} 𝑥 ∈𝑋 𝑗 𝑗. = max {𝐴̃′ ∘ 𝑅̃𝑖 } 𝑖∈{1,⋯,𝑚}. = 𝜇 ⋃𝑚 ̃′ ̃ (𝑦) 𝑖=1(𝐴 ∘𝑅𝑖 ) ̃ ∘ ⋃𝑚 𝑅̃𝑖 = ⋃𝑚 (𝐴̃′ ∘ 𝑅̃𝑖 ) = ⋃𝑚 𝐵′ ̃ 𝑖 , di mana untuk setiap 𝑦 ∈ 𝑌. Jadi 𝐵̃′ = 𝐴′ 𝑖=1 𝑖=1 𝑖=1 ̃ 𝑖 = 𝐴̃′ ∘ 𝑅̃𝑖 . 𝐵′ Jika untuk implikasi kabur 𝑅̃𝑖 tersebut diambil implikasi Mamdani →𝑚𝑚 , sehingga fungsi keanggotaannya adalah 𝜇𝑅̃𝑖 (𝑥1 , ⋯ , 𝑥𝑛 , 𝑦) = min {𝜇𝐴̃𝑖1×⋯×𝐴̃ (𝑥1 , ⋯ , 𝑥𝑛 ), 𝜇𝐵̃𝑖 (𝑦)}, 𝑖𝑛. maka fungsi keanggotaan 𝐵̃ ′ adalah 𝜇𝐵̃′ (𝑦) = 𝜇⋃𝑚 ̃′ ̃ (𝑦) 𝑖=1 𝐴 ∘𝑅𝑖 =. max. sup min{𝜇𝐴̃′1×⋯×𝐴̃′𝑛 (𝑥1 , ⋯ , 𝑥𝑛 ), min(𝜇𝐴̃𝑖1×⋯×𝐴̃𝑖𝑛 (𝑥1 , ⋯ , 𝑥𝑛 ), 𝜇𝐵̃𝑖 (𝑦))}. 𝑖∈{1,⋯,𝑚} 𝑥 ∈𝑋 𝑗 𝑗. = max. sup min { min (𝜇𝐴̃′𝑗 (𝑥𝑗 )), min ( 𝜇𝐴̃𝑖𝑗 (𝑥𝑗 )), 𝜇𝐵̃𝑖 (𝑦)}. 𝑖∈{1,⋯,𝑚} 𝑥 ∈𝑋 𝑗 𝑗. 𝑗∈{1,⋯,𝑛}. = max min { min 𝑖∈{1,⋯,𝑚}. sup. 𝑗∈{1,⋯,𝑛}. min (𝜇𝐴̃′𝑗 (𝑥𝑗 ), 𝜇𝐴̃𝑖𝑗 (𝑥𝑗 )), 𝜇𝐵̃𝑖 (𝑦)}. 𝑗∈{1,⋯,𝑛} 𝑥 ∈𝑋 𝑗∈{1,⋯,𝑛} 𝑗 𝑗. = max min{𝑤𝑖 , 𝜇𝐵̃𝑖 (𝑦)} 𝑖∈{1,⋯,𝑚}. dengan 𝑤𝑖 = min 𝑤𝑖𝑗 dan 𝑤𝑖𝑗 = sup 𝑗∈{1,⋯,𝑛}. 𝑖 = 1, ⋯ , 𝑚.. min ( 𝜇𝐴̃′𝑗 (𝑥𝑗 ), 𝜇𝐴̃𝑖𝑗 (𝑥𝑗 )),. 𝑥𝑗 ∈𝑋𝑗 𝑗∈{1,⋯,𝑛}.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 37. Nilai 𝑤𝑖𝑗 = sup (𝐴̃′𝑗 ∩ 𝐴̃𝑖𝑗 ) merupakan derajat keserasian (degree of 𝑥𝑗 ∈𝑋𝑗. compatibility) antara fakta 𝐴̃′𝑗 yang diberikan dengan anteseden 𝐴̃𝑖𝑗 dari premis/kaidah 𝑅̃𝑖 , sedangkan 𝑤𝑖 yang merupakan minimum dari semua 𝑤𝑖𝑗 untuk 𝑗 = 1, ⋯ 𝑛. seringkali disebut daya sulut (firing strength) yang. menyatakan sejauh mana anteseden dari kaidah 𝑅̃𝑖 dipenuhi oleh fakta 𝐴̃′ yang diberikan dan menyulut konsekuen dari kaidah tersebut. Dengan demikian kesimpulan 𝐵̃′ ditentukan dengan empat langkah sebagai barikut: Langkah 1. : Tentukan derajat keserasian 𝑤𝑖𝑗 , yaitu supremum dari 𝐴̃′𝑗 ∩ 𝐴̃𝑖𝑗 untuk setiap 𝑖 = 1, ⋯ , 𝑚 dan 𝑗 = 1, ⋯ , 𝑛.. Langkah 2. : Untuk setiap i, tentukan daya sulut 𝑤𝑖 sebagai minimum dari semua derajat keserasian 𝑤𝑖𝑗 (𝑗 = 1, ⋯ , 𝑛).. Langkah 3. : Untuk setiap i, tentukan irisan 𝑤𝑖 dengan 𝐵̃𝑖 .. Langkah 4. : Gabungkanlah semua irisan tersebut untuk memperoleh 𝐵̃′ .. F. Sistem Inferensi Kabur Salah satu aplikasi logika kabur yang telah berkembang amat luas dewasa ini adalah sistem inferensi kabur, yaitu sistem komputasi yang bekerja atas dasar penalaran kabur, misalnya sistem kendali otomotis, sistem klasifikasi data, sistem pakar, sistem pengenalan pola, robotika, dan sebagainya. Sistem kendali ini berfungsi untuk mengendalikan proses tertentu dengan mempergunakan aturan inferensi berdasarkan logika kabur. Pada dasarnya sistem kendali semacam itu terdiri dari empat unit, yaitu: 1. Unit pengaburan (fuzzification unit) 2. Unit penalaran logika kabur (fuzzy logic reasoning unit) 3. Unit basis pengetahuan (knowledge base unit), yang terdiri dari dua bagian: a. Basis data (data base), yang memuat fungsi-fungsi keanggotaan dari himpunan-himpunan kabur yang terkait dengan nilai dari variabel-variabel linguistik yang dipakai. b. Basis kaidah (rule base), yang memuat kaidah-kaidah berupa implikasi kabur..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 38. 4. Unit Penegasan (defuzzification unit). Suatu sistem kendali semacam itu mula-mula mengukur nilai-nilai tegas dari semua variabel masukan yang terkait dalam proses yang akan dikendalikan. Nilai-nilai itu kemudian dikonversikan oleh unit pengaburan ke nilai kabur yang sesuai. Hasil pengukuran yang telah dikaburkan itu kemudian diproses oleh unit penalaran, yang dengan menggunakan unit basis pengetahuan, menghasilkan himpunan (himpunan-himpunan) kabur sebagai keluarannya. Langkah terakhir dikerjakan oleh unit penegasan, yaitu menerjemahkan himpunan (himpunanhimpunan) kabur keluaran itu ke dalam nilai (nilai-nilai) yang tegas. Nilai tegas inilah yang kemudian direalisasikan dalam bentuk suatu tindakan yang dilaksanakan dalam proses pengendalian itu.. Selanjutnya akan dibahas masing-masing unit tersebut. 1. Unit Pengaburan Langkah pertama pada sistem kendali kabur logika kabur adalah mengubah nilai variabel masukan yang tegas (yang biasa dinyatakan dalam bilangan real) menjadi nilai pendekatan yang kabur. Untuk itu digunakan fungsi pengaburan, yaitu pemetaan 𝑓: ℝ → 𝐾, dengan 𝐾 dalah suatu kelas himpunan kabur dalam semesta ℝ. Fungsi pengaburan itu biasanya ditentukan berdasarkan beberapa kriteria: a.. Fungsi pengaburan diharapkan mengubah suatu nilai tegas, misalnya 𝑎 ∈ ℝ, ke suatu himpunan kabur 𝐴̃ dengan 𝜇𝐴̃ (𝑎) = 1 atau sekurang-kurangnya 𝑎 mempunyai derajat keanggotaan yang tinggi.. b.. Bila nilai masukannya cacat karena derau, diharapkan fungsi pengaburan dapat menekan sejauh mungkin derau itu.. c.. Fungsi pengaburan diharapkan dapat membantu menyederhanakan komputasi yang harus dilakukan oleh sistem tersebut dalam proses inferensinya.. Berikut diberikan beberapa contoh fungsi pengaburan. a.. Fungsi Pengaburan Segitiga memetakan nilai 𝑎 ∈ ℝ ke himpunan kabur 𝐴̃ dengan fungsi keanggotaan berbentuk segitiga samakaki, yaitu 𝜇𝐴̃ (𝑥 ) = 𝑆𝑒𝑔𝑖𝑡𝑖𝑔𝑎(𝑥; 𝑎 − 𝜎, 𝑎, 𝑎 + 𝜎).

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 39. dengan 𝜎 adalah suatu parameter berupa bilangan positif yang menentukan lebarnya pendukung dari himpunan kabur tersebut. b.. Fungsi Pengaburan Gauss yang memetakan nilai 𝑎 ∈ ℝ ke himpunan kabur 𝐴̃ dengan fungsi keanggotaan Gauss, yaitu 𝜇𝐴̃ (𝑥 ) = 𝐺𝑎𝑢𝑠𝑠(𝑥; 𝑎, 𝑏) = 𝑒 −(. 𝑥−𝑎 2 ) 𝑏. dengan 𝑏 adalah suatu parameter berupa bilangan positif. c.. Fungsi Pengaburan Elemen Tunggal memetakan nilai tegas 𝑎 ∈ ℝ ke himpunan kabur 𝐴̃ dengan fungsi keanggotaan 1 jika 𝑥 = 𝑎 𝜇𝐴̃ (𝑥 ) = { 0 jika 𝑥 ≠ 𝑎 untuk setiap 𝑥 ∈ ℝ. Jadi sebenarnya himpunan kabur 𝐴̃ ini adalah himpunan tegas dengan elemen tunggal, yaitu 𝐴̃ = {𝑎}.. 2. Unit Basis Pengetahuan Unit basis pengetahuan dari suatu sistem kendali logika kabur terdiri dari basis data dan basis kaidah. Basis data adalah himpunan fungsi-fungsi keanggotaan dari himpunan-himpunan kabur yang terkait dengan nilai-nilai linguistik dari variabel-variabel yang terlibat dalam sistem itu. Sedangkan basis kaidah adalah himpunan implikasi-implikasi kabur yang berlaku sebagai kaidah dalam sistem itu. Bila sistem itu mempunyai m buah kaidah dengan (𝑛 + 1) variabel, maka bentuk umum kaidah ke-𝑖 (𝑖 = 1, ⋯ , 𝑚) adalah sebagai berikut: 𝐵𝑖𝑙𝑎 𝑥1 adalah 𝐴𝑖1 dan ⋯ ⋯ dan 𝑥𝑛 adalah 𝐴𝑖𝑛 , maka 𝑦 adalah 𝐵𝑖 dengan 𝑥𝑗 adalah variabel linguistik dengan semesta numeris 𝑋𝑗 (𝑗 = 1, ⋯ , 𝑛). Suatu basis kaidah diharapkan memenuhi beberapa kriteria sebagai berikut: a. Lengkap, yaitu setiap (𝑥1 , ⋯ , 𝑥𝑛 ) ∈ 𝑋1 × 𝑋2 × ⋯ × 𝑋𝑛 terdapat 𝑖 ∈ {1, ⋯ , 𝑚} sedemikian sehingga 𝜇𝐴̃𝑖𝑗 (𝑥𝑗 ) ≠ 0 untuk semua 𝑗 ∈ {1, ⋯ , 𝑛}. Dengan perkataan lain, untuk setiap nilai masukan terdapat sekurang-kurangnya satu kaidah yang “tersulut”. b. Konsisten, yaitu tidak terdapat kaidah-kaidah yang mempunyai anteseden yang sama tetapi konsekuennya berbeda..

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 40. c. Kontinu, yaitu tidak terdapat kaidah-kaidah dengan himpunan-himpunan kabur yang terkait dalam anteseden beririsan, tetapi himpunan-himpunan kabur yang terkait dalam konsekuennya saling asing. 3. Unit Penalaran Kabur Masukan kabur hasil pengolahan unit pengaburan diterima oleh unit penalaran untuk disimpulkan berdasarkan kaidah-kaidah yang tersedia dalam unit basis pengetahuan. Penarikan kesimpulan itu dilaksanakan berdasarkan aturan modus ponens rampat multikondisional dengan skema sebagai berikut: Kaidah 1. : Bila 𝑥1 adalah 𝐴11 dan ⋯ dan 𝑥𝑛 adalah 𝐴1𝑛 , maka y adalah 𝐵1. Kaidah 2. : Bila 𝑥1 adalah 𝐴21 dan ⋯ dan 𝑥𝑛 adalah 𝐴2𝑛 , maka y adalah 𝐵2. ⋮. ⋮. ⋮. Kaidah m. : Bila 𝑥1 adalah 𝐴𝑚1 dan ⋯ dan 𝑥𝑛 adalah 𝐴𝑚𝑛 , maka y adalah 𝐵𝑚. Fakta. : 𝑥1 adalah 𝐴′1 dan ⋯ dan 𝑥𝑛 adalah 𝐴′𝑛. Kesimpulan. : y adalah 𝐵′. dengan 𝐴𝑖𝑗 dan 𝐴′𝑗 adalah predikat kabur yang dikaitkan dengan himpunan kabur 𝐴̃𝑖𝑗 dan 𝐴̃′𝑗 dalam semesta 𝑋𝑗 dan 𝐵𝑖 adalah predikat kabur yang dikaitkan dengan himpunan. kabur. 𝐵̃𝑖. dalam. semesta. 𝑌 (𝑖 = 1, ⋯ , 𝑚, 𝑗 = 1, ⋯ , 𝑛).. Jika. ̃ = 𝐴′ ̃ 1 × ⋯ × 𝐴′ ̃ 𝑛 dalam fakta/masukannya dinyatakan dengan himpunan kabur 𝐴′ 𝑋1 × ⋯ × 𝑋𝑛 , masing-masing kaidah dinyatakan dengan relasi kabur 𝑅̃𝑖 (𝑖 = 1, ⋯ , 𝑚) dalam 𝑋1 × ⋯ × 𝑋𝑛 × 𝑌, dan 𝑅̃ = ⋃𝑛𝑖=1 𝑅̃𝑖 , maka kesimpulan/keluaran “y adalah 𝐵′” dapat diperoleh dengan mempergunakan kaidah inferensi komposisional ̃ = 𝐴′ ̃ ∘ 𝑅̃ dalam Y. untuk menentukan himpunan kabur 𝐵′ 4. Unit Penegasan Kesimpulan/keluaran dari sistem kendali kabur adalah suatu himpunan kabur. Karena sistem tersebut hanya dapat mengeksekusikan nilai yang tegas, maka diperlukan suatu mekanisme untuk mengubah nilai kabur keluaran itu menjadi nilai yang tegas. Itulah peranan unit penegasan yang memuat fungsi-fungsi penegasan dalam sistem itu. Fungsi penegasan adalah suatu pemetaan 𝑡: 𝐾 → ℝ, dengan 𝐾 adalah suatu kelas himpunan-himpunan kabur, yang memetakan suatu himpunan kabur. ke suatu bilangan real yang tegas. Bilangan ini menentukan tindakan.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 41. pengendalian yang harus dilakukan oleh sistem itu. Pemilihan fungsi penegasan biasanya ditentukan oleh beberapa kriteria: a. Masuk akal, artinya secara intuitif bilangan tegas 𝑡(𝐴̃) dapat diterima sebagai bilangan yang mewakili himpunan kabur 𝐴̃ , misalnya: 𝑡(𝐴̃) kurang-lebih berada di tengah-tengah Pendukung(𝐴̃), atau 𝑡(𝐴̃) mempunyai derajat keanggotaan yang tinggi dalam himpunan kabur 𝐴̃ . b. Kemudahan komputasi, yaitu diharapkan fungsi penegasan itu cukup mudah dan sederhana dalam proses komputasinya untuk menghasilkan bilangan tegas keluarannya. c. Kontinyu, artinya perubahan kecil pada 𝐴̃ tidak akan mengakibatkan perubahan besar pada 𝑡(𝐴̃). Dalam literatur dikenal beberapa fungsi penegasan, di antaranya a-dalah: a.. Purata Maksimum (Mean of Maximum): Himpunan kabur 𝐴̃ dalam semesta ℝ diubah menjadi bilangan tegas 𝑡(𝐴̃) yang merupakan purata dari semua nilai yang mencapai nilai maksimum dalam 𝜇𝐴̃ , yaitu 𝑟. 𝑡(𝐴̃) =. ∫𝑀 𝑥 𝑑𝑥 𝑟. ∫𝑀 𝑑𝑥. dengan 𝑀 = {𝑥 ∈ ℝ│𝜇𝐴̃ (𝑥 ) = 𝑇𝑖𝑛𝑔𝑔𝑖(𝐴̃)} dan ʃ adalah notasi integral biasa dalam kalkulus. Apabila 𝑀 = [𝑎, 𝑏], maka 𝑏. 𝑡(𝐴̃) =. ∫𝑎 𝑥 𝑑𝑥 𝑏. ∫𝑎 𝑑𝑥 1. =. [ 2𝑥 2 ]. 𝑏 𝑎. [𝑥]𝑏 𝑎. 1 2 (𝑏 − 𝑎2 ) =2 𝑏−𝑎 1 (𝑏 + 𝑎)(𝑏 − 𝑎) =2 𝑏−𝑎.

PLAGIAT MERUPAKAN TINDAKAN TIDAK TERPUJI 42. 𝑡(𝐴̃) =. 𝑎+𝑏 2. Apabila himpunan kabur 𝐴̃ terdefinisi pada semesta diskret berhingga 𝑋 = {𝑥1 , 𝑥2 , ⋯ , 𝑥𝑛 }, maka bilangan tegas 𝑡(𝐴̃) didefinisikan sebagai rerata dari semua nilai 𝑥𝑖 dalam himpunan tegas 𝑀 = {𝑥𝑖 𝜖𝑋│𝜇𝐴̃ (𝑥𝑖 ) = 𝑇𝑖𝑛𝑔𝑔𝑖(𝐴̃)}, yaitu 𝑡(𝐴̃) =. ∑𝑥𝑖 ∈𝑀 𝑥𝑖 |𝑀 |. dengan |𝑀| menyatakan banyaknya anggota dari himpunan tegas M. b. Pusat Gravitasi (Center of Gravity): Himpunan kabur 𝐴̃ dalam semesta ℝ diubah menjadi bilangan tegas 𝑡(𝐴̃) yang merupakan absis dari pusat gravitasi daerah di bawah grafik fungsi keanggotaan himpunan kabur 𝐴̃ . Jadi 𝑟. 𝑡(𝐴̃) =. ∫𝑥 𝜇𝐴̃ (𝑥)𝑥 𝑑𝑥 𝑟. ∫𝑥 𝜇𝐴̃ (𝑥 )𝑑𝑥. .. Bila himpunan kabur 𝐴̃ terdefinisi pada semesta diskret berhingga 𝑋 = {𝑥1 , 𝑥2 , ⋯ , 𝑥𝑛 }, maka 𝑡(𝐴̃) =. ∑𝑛𝑖=1 𝜇𝐴̃ (𝑥𝑖 ) 𝑥𝑖 ∑𝑛𝑖=1 𝜇𝐴̃ (𝑥𝑖 ). Nilai 𝑡(𝐴̃) ini dapat dipandang sebagai nilai harapan dari variabel x.. c.. Rerata Pusat (Center Average): Jika himpunan kabur 𝐴̃ dalam semesta ℝ ̃ merupakan gabungan dari m buah himpunan kabur, yaitu 𝐴̃ = ⋃𝑚 𝑖=1 𝐴𝑖 , maka 𝐴̃ diubah menjadi bilangan tegas 𝑡(𝐴̃) yang merupakan rerata terbobot dari pusat-pusat m buah himpunan kabur tersebut, dengan tinggi masing-masing himpunan kabur itu sebagai bobotnya. Jadi 𝑡(𝐴̃) =. ∑𝑚 𝑖=1 𝑏𝑖 𝑥𝑖 ∑𝑚 𝑖=1 𝑏𝑖. dengan 𝑥𝑖 adalah pusat dari himpunan kabur 𝐴̃𝑖 dan 𝑏𝑖 = 𝑇𝑖𝑛𝑔𝑔𝑖(𝐴̃𝑖 )..