Metode daerah kepercayaan untuk menyelesaikan masalah optimasi tanpa kendala - USD Repository

METODE DAERAH KEPERCAYAAI\I T]NTT]K MEI\TYELESAIKAII MASALAH

OPTIMASI TAI\PA KEI\IDALA

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun Oleh: Christiansen Pasaribu

N I M : 0 5 3 1 1 4 0 1 9

PROGRAM STT]DI MATEMATIKA JI]RUSAI\I MATEMATIKA X'AKT]LTAS SAINS DAI\[ TEKNOLOGI

T]NTVERSITAS SANATA DHARMA YOGYAKARTA

TRUST-REGION METHODS TO SOLVE

I]NCONSTRAINED OPTIMIZATION PROBLEMS

THESIS

Presented as Partial Fulfillment of the Requirements To Obtainthe SARIANA SAINS Degree

In Mathematics

B y :

Christiansen Pasaribu Student Number : 053 1 14019

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT SCIENCE AI\[D TECHNOLOGY FACULTY

SKRIPSI

MET(X)N DAERAH KEPERCAYAA}{

UNTT]K MEFTYELESAIKAN MASALAH OPTIMASI TANPA KEFIDALA

"tf-

s.si.,

M.si.

_{Tanggal 22 Juli 2009}

lll

P' **

qM

fux

Ketua Sekretaris Anggota

SKRIPSI

METODE DAERAH KEPERCAYAAI{

TINTUK MEII-YELESAIKAI\ MASALAH OPTIMASI TAITPA KENIDALA

: St. Eko Hari Paruradi, S.Si., M.Kom. : LusiaKrismiyati Budiasih, S.Si., M.Si.

Yogyakarta 29 Juli 2009 Fakultas Sains dan Teknologi Universius $anata Dhmma

'P{*'^

Dipersiapkan dan ditulis oleh :

PER}TYATAAI\I KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain" kecuali yang telah disebutkan dalam kutipan dan daftax pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta" 22 hili2009 Penulis,

KUPERSEMBAHKAN SKR/,PS' INI KEPADA:

TUHAN YESUS KRISTUS

BAPAK DAN MAMATERC'NTA ATAS SEMANGAT, DOA, SERTA DUKUNoAN SECARA MORIL MAUPUN MATERI'L

ABANGKU TERC'NTA WHARTON FRED'CKSEN P,6AR'BU

KEDUA ADIKKU TERC'NTA WALD'MER PASAR'BU DAN CAROLINA PASARIBU

ALMAMATERKU UN'VERS'TAS SANATA DHARMA

MATA GURU ROHA SISEAN

IaIcm BERDOA AGAR HIDUP LEBIH MUDAH. Bnnoos.en AGAR KITA LEBrH

KUAT

{fonu F. Krnwnnv)

Hrnup rru sEpERTr SEBUAH snpnot Kau

TIDAKAKAN TERJATUH KECUA"II BILA BERHENTI MENGAYUH

( Crnuoe Pnnnnn)

TnRruRrRsrH DAN Kesm^nxnr rETAp

MENIADI IGKUATAN TERBESAR DUNIA

( Frunorucn oRRr Boormcnwrncn ₎

LEMBAR PERIYYATAAI\ PERSETUJUAI\

PUBLIKASI KARYA ILMIAH I]NTI]K KEPENTINGAI\I AKADEMIS

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma: Nama : Christiansen Pasaribu

Nomor Mahasiswa : 053114019

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma kwyailmiah saya yang berjudul:

METODE DAERAH KEPERCAYAAN T]NTI'K MEIYYELESAIKAI\ MASALAH

OPTIMASI TAI\PA KENDALA

Beserta perangkat yang diperlukan (bila ada). Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan da@ mendistribusikan secara terbatas, dan mempublikasikan di Internet atau media lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun memberikan royalti kepada saya selamatetap mencantumkan nama saya sebagai penulis.

Demikian pemyataan ini saya buat dengan sebenarnya. Dibuat di Yogyakarta.

Pada Tanggal:29 Juli 2009 Yang menyatakan

W ^ r*.,{i-rn l1.z

( \ ) 4 1 Ww- ll_w

| ^ ^ - l q

/ I I Y W t / !

(Christiansen Pasaribu)

ABSTRAK

Optimasi fungsi multivariabel tidak mudah diselesaikan secaxa analitik. Tetapi bukan berarti masalah tersebut tidak dapat diselesaikan. Pada skripsi ini akan diperkenalkan suatu metode numerik yang dapat menyelesaikan masalah tersebut yakni Metode Daerah Kepercayaan. Dalam Metode Daerah Kepercayan masalah optimasi fungsi multivariabel diubah menjadi masalatr dalam bentuk kuadratih yakni dengan membangun sebuah model fungsi kuadratik. Metode Daerah Kepercayaan adalalt suatu metode iterasi yang mendefinisikan suatu daeratr pada iterasi yang sedang berlangsung yang dipercayai memuat calon solusi dari suatu model yang menjadi representasi yang baik dari fungsi objektif. Perhitungan pada model ini bertujuan untuk mencari sebuah langkah yang menjadi peminimal hampiran dari model kuadratik tersebut. Jika langkah tidak cocok maka ukuran daerah kepercayaan diperkecil dan mencari peminimal baru. Solusi dari masalah optimasi yang sebenarnya diperoleh dengan menjumlahkan vektor langkah yang baru dengan solusi pada iterasi yang sebelumnya. Metode ini juga mempunyai sifat konvergen global.

ABSTRACT

The optimization function multivariables is not easy to solved with analysis. But it doesn't mean that the problem can not solved. In this thesis will introduced a numerical method can solve the problem which is Region Method. In Trust-Region Method, optimization problem function multivariables change into quadratic problem, wtrich is with construct a quadratic model function. Trust-Region Method is an iterative method which define a region around from current iterate which trusted load the solution candidate from a model to be a good representation of the objective function. Calculating in this model to find a step to be the approximate minimize of the quadratic model. If the step does not acceptable then size of the trust region would be reduced and find a new minimizer. Solution of the actually optimization problem obtained by summing a new step with the solution of previous iteration. This method also have global convergent characteristic.

KATA PENGAI\ITAR

Segala puji dan syukur, penulis panjatkan kepada Tuhan Yesus Kristus, Sang Juru Selamat, sehingga karena kasih dan karunia-Nya skripsi ini dapat diselesaikan dengan baik.

Dalam penyusurum skripsi ini penulis membutuhkan bantuan dari berbagai pihak. Oleh karena itu, dengan segala kerendahan hati penulis ingin menyampaikan ucapan terima kasih kepada :

l. Lusia Krismiyati Budiasih, S.Si., M.Si., selaku dosen pembimbing dan Kaprodi Matematika FST-USD yang dengan rendah hati mau banyak waktu dan penuh kesabaran telah membimbing penulis selama penyusumn skripsi. 2. Yosef Agung Cahyanta S.T., M.T., selaku Dekan FST-USD.

3. Ch. Enny Mwwaningtyas, S.Si., M.Si., selaku dosen penguji. 4. St. Eko Hari Parmadi, S.Si., M.Kom., selaku dosen penguji.

5. Romo Prof. Dr. Frans Susilo, S.J., selaku dosen pembimbing akademik.

6. Sudi Mungkasi, S.Si., M.Sc., yang pemah menjadi dosen pembimbing akademik bagi penulis.

7. Y.G. Hartono, S.Si., M.Sc., dan Herry Pribawanto Suryawan" S.Si., M.Si.o ymg telah banyak membantu dan memberi masukan kepada penulis.

8. Bapak dan Ibu dosen Prograrn Studi Matematika yang telah memberikan bekal ilmu yang sangat berguna bagi penulis.

10. Kedua orang tuaku serta abangku Wharton dan adik-adikku Waldimer dan Carolina yang selalu memberikan dukungan kepadaku dan untuk semua pelajaran hidup, cintq kasih sayang, pengorbanan, doa motivasi dan kepercayaan yang sangat berarti.

11. Ratna Bunga atas waktu dan dukungan yang selama ini diberikan kepada penulis.

12. Teman-teman Matematika angkatan 2005 : Ratra George, Louis, Vincent, Priskila" Dedy, Zetho, Yudi, Sisiria, Inne, Echi, Susi, Devi, Wuri, Septi, Tyas, Nanin, Puput, Shela" Vira.

13. Teman-teman Matematika baik kakak angkatan maupun adik angkatan.

14. Teman-temanku : Boy, Buyo, Dedeo, Suadq Dani, Anes, Paranso, Ari, Romi, dan Wawan.

15. Semua pihak yang telah membantu yang tidak dapat disebutkan satu persatu.

Penulis menyadari masih ada kekurangan dalam skripsi ini, untuk itu saran serta kritik yang membangun sangat diharapkan dalam peningkatan kualitas skripsi ini, dan akhimya penulis berharap semoga skripsi ini dapat bermanfaat bagi semua pihak.

Yogyakarta 29 Juli 2009

Penulis,

/E/ 4)

IMAWW

I V A

Y

t^-\

Christiansen Pasaribu

DAFTAR ISI

}II{LAIvI{N JUDUL

HALAMAN JUDUL DALAM BAHASA INGGRIS HALAMAN PERSETUruAN PEMBIMBING ... HALAMAN PENGESAHAN

PERNYATAAN KEASLIAN KARYA HALAMAN PERSEMBAHAN

LEMBAR PERNYATAAN PERSETUruAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ...

ABSTRAK ABSTRACT

KATA PENGANTAR ... DAFTAR ISI ...

DAFTAR GAMBAR DAFTAR TABEL

BAB I PENDAHULUAN A. Latar Belakang Masalah B. Perumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Metode Penulisan

Manfaat Penelitian Sistematika Penulisan

BAB II RUANG VEKTOR MATRIKS. DAN TEORI OPTIMASI A. Ruang Vektor dan Matriks...

B. Diferensial Fungsi Kontinu.... C. Masalah Optimasi...

D. Optimasi Tanpa Kendala.... E. Metode Newton...

BAB III METODE DAERAH KEPERCAYAAN IJNTUK MENYELESAIKAN MASALAH OPTIMASI

TANPA KENDALA

A. Metode Daerah Kepercayaan

B. Algoritma Metode Daeratr Kepercayaan

C. Kekonvergenan pada Metode Daerah Kepercayaan ... BAB IV PENUTUP

A. Kesimpulan ... B. Saran

DAT"TARGAMBAR

Halaman

Garnbar z.z.1ctrafikTeoremaNilai Rata-rata 15

Gambar 2.4.1 Macarn-macam titik peminimal... 25 Garnbar 2.5.1 Diagrarn Alir Algoritna Metode Newton... 30 Gambar 3.2.1 Diagram Alir Algoritna Metode Daerah Kepercayaan 46

DAFTAR TABEL

Halaman Tabel 3.2.1 Output penyelesaian contoh 3.2.1 dengan Matlab. 55

Tabel 3.3.1 Tabel perbandingan nilai awal. 69

BAB I PENDAHULUAI\I

A. LatarBelakang Masalah

ditemukan nilai-nilai variabel yang dapat mengoptimalkan fungsi tersebut. Namun pengoptimalan fungsi objektif dapat dilakukan meskipun tidak ada kendala yang terlibat. Pengoptimalan pada kondisi ini disebut juga pengoptimalan tanpa kendala. Untuk menyelesaikan masalah optimasi tanpa kendala ada beberapa metode yang dapat digunakan, misalnya metode Newton, metode Turun Tercuram, metode Broyden, metode Pencarian Garis, dan metode Daerah Kepercayaan. Dalam penulisan skripsi ini, metode yang akan dibahas adalah metode Daerah Kepercayaan. Pengoptimalan dari model ini dapat dilakukan dengan memeriksa setiap x € IRn yang meminimalkan rulai f (x). Namun hal tersebut membutuhkan waktu yang lama untuk

a. Untuk mengatasi hal ini, dipilih suatu titik x* e IR? yang membuat nilai fungsi/paling minimum. Kemudian akan diperiksa nilai fungsi f (x) di titik-titik sekitarnya. Pemeriksaan nilai tungsi f (*) di titik-titik

sekitarnya dapat dilakukan dengan menggunakan suatu algoritma. Untuk itu persamaan tersebut dapat dinyatakan dalam suatu model fungsi mp.Model mp ini mempunyai sifat yang sama dengan fungsi/di titik-titik sekitar x. Akan dipilih satu daerah di sekitar x dengan mencari nilai p yang meminimumkan m(x+ p) sebagai pendekatan.

B. Perumusan Masalah

Bagaimana menyelesaikan masalah optimasi tanpa kendala menggunakan metode daerah kepercayaan?

Bagaimana algoritna metode daerah kepercayaan dan implementasinya menggunakan batrasa pemrograman Mafl ab?

C. Batasan Masalah

Pernbahasan masalah metode daerah kepercayaan dalam skripsi ini hanya dibatasi pada model kuadratik dan pada masalah optimasi tanpa kendala.

Tujuan Penulisan

Tujuan penulisan skripsi ini adalah untuk menyelesaikan masalah optimasi tanpa kendala dengan menggunakan metode daerah kepercayaan dan untuk menyusun algoritrna metode daerah kepercayaan menggunakan bahasa pemrogftrman Matlab.

E. Metode Penulisan

Metode penulisan skripsi ini menggunakan metode studi pustak4 yaitu dengan menggunakan buku-buku pendukung yang berkaitan dengan metode daerah kepercayaan dan menuliskan programnya dengan bahasa pernrogmman Matlab.

t .

F. Manfaat Penulisan

Manfaat penulisan skripsi ini adalah untuk memperoleh pengetahuan tentang metode daerah kepercayaan dan menambah daftar referensi metode yang digunakan untuk menyelesaikan masalah optimasi tanpa kendala dalam hal ini metode daerah kepercayaan, serta mempermudah penggunaan metode ini dengan algoriuna bahasa pemrogranum Matlab.

G. Sistematika Penulisan BAB I PEI\DAHULUAI\

A. Latar Belakang Masalatr B. Perumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Metode Penulisan F. Manfaat Penulisan G. Sistematika Penulisan

BAB II RUANG VEKTO& MATRIKS, DAf[ TEORI OPTIMASI A. Ruang vektor dan Matriks

B. Diferensial Fungsi Kontinu C. Masalah Optimasi

BAB III METODE DAERAH KEPERCAYAAIT T]NTT]K MEI\TYELESAIKAI\I MASALAII OPTIMASI TAI\IPA KENDALA

A. Metode Daerah Kepercayaan

B. Algorinna Metode Daerah Kepercayaan

C. Kekonvergenan pada Metode Daerah Kepercayaan

BAB II

RUANG VEKTO& MATRTKS, DAf[ TEORr OprrMASr

Dalam bab ini akan dibahas mengenai ruang vektor, matriks, nonna, kalkulus, masalah optimasi, optimasi tanpa kendala, metode Newton. Definisi, teorema serta konsep - konsep mengacu padadaftar pustaka.

A. Ruang Vektor dan Matriks

Pada subbab ini akan dibahas mengenai sifat-sifat vektor, nonnq dan matiks. Definisi 2.1.1

Misalkan V adalah suatu himpunan tak kosong dengan dua operasi:

(i) penjumlahan vektor: untuk sebarang x, y € I/, hasil penjumlahan x * y e V. (ii) perkalian skalar: untuk sebarang x € 7 dan suatu skalar a e R, hasilkali

a x € V .

maka Z disebut ruang vektor jika aksioma-aksioma berikut dipenuhi untuk sebarang x,y,z C V dn sebarang skalar a, b e IR.

1. x+y:y + xuntuk setiap x dan y dtV

2. (x + y) + z: x + (y + z) untuk setiap x,y,z di Y.

3. Terdapatelemen0 di Zsehinggax+0=xuntuksetiap xe V.

4. Untuk setiap x € Zterdapat elemen (-x) e Zsehingga x + (-x): g. 5. a(x +y) : ax + ary untuk setiap skalara € lR dan setiap x dan y di V.

6. (a + b)x= crx+ 6x untuk setiap skalar a dan 6 e R. dan setiap x e V.

7. (ab) x= a (bx) untuk setiap skalar a danb € R dan setiap x € V.

Delinisi 2.1.2

Hasil kali dalam baku untuk lRn adalah hasil kali skalar (*,y): x"y

De{inisi 2.1.3

Jika vektor u : (u1,1t2,...,un) dan vektor v : (v1,t22,...,vn)adalah sebarang vektor dalam IRt, maka hasit kali dalam Euctidean

u . v: (uft * u2v2 + ...+ It"v")

Delinisi 2.1.4

Irka V adalah sebuah ruang hasil kali dalam, maka nonna (norm) atau panjang (length) sebuah vektor u di dalam V dinotasikan dengan llull dan didefinisikan sebagai

llull - (u, uf/z = (u ' u)tlz

Misalkan vektor u: (zl u2)makanorma dari suatu vektor u = (arl, u) adalertt

ffufl=JW,

Jarak Euclidean antara vektor a : (u1,"u2, ...,un) dan vektor v : (v1,112, .,, ,1)n)

d ( a , v ) : l l u - o 1 1 :

Definisi 2.1.5

Sebuah ruang vektor Zdikatakan ruang linear bernorma (normed linear space) jika untuk setiap vektor v EV dikaitkan dengan sebuah bilangan _{real tlvll yang}

disebut noflna dari v yang memenuhi :

(t) llvll ) 0 dengan kesamaan berlaku jika dan hanya jika v = 0. (Z) llcvll = lal llvll untuk semrn skalar a.

(3) llv + wll < llvll + llwll ini disebut Ketaksamaan segitiga. Beberapa contoh norma vektor

1. Nomra jumlah (11 nomr) di Rl.

\-t

llxl[: /lxil

i = t

2. Norma tak terbatas (l* norm) di IRn.

llxll- = mgllxrl

3. Norma lo (1, norm) di Rn.

4. Norma 12 (12 norm) di IRtr.

9

ttxttz

= (t,,.,,')"'

Definisi 2.1.6

Suatu matriks bujur sangkar,4 adalah simetrik jika A = Ar .

Definisi 2.1.7

Misal A e IR.nm adalah matriks simetrik.

A dikatakan _{definit positifjika vrAv > 0, V v € IRn, v # 0.} A dikatakan semidefinit positifjika vrAv > 0, V v € IRn, v # 0. A dikatakan _{definit negatifjika vrAv < 0, V v € IRn, y # 0.} A dikatakan semidefinit negatifjika vrAv < 0, V v € lRn, v # 0.

A dikatakan indefinit jika tidak semidefinit positif atau semidefinit negatif.

Defrnisi 2.1.8

Misalkan A,Be lR.mtn. Suatu pemetaan ll.ll:Rm+R dikatakan noflna matriks jika memenuhi sifat

(i) ll,4ll > 0,vA e lR*; A = }jika dan hanya jika A = 0;

(ii) llaAll - lalllAll,va e &A € lR*;

(iii) ll/ + Bll < lFll + llBll,vA,B

e rRmrn.

Beberapa contoh norma matriks

1 0

m

ilAilr

= pmzl",t

2. Norma 12 untuk Ayttgdidefinisikan dengan

tf,altz

= (7*n 7a, e1)'/'

dengan.l merupakan _{nilai eigen dari matriks ^4.} 3. Norma l* untukA yang didefinisikan dengan

ll/ll- =

-e* ilo,il

j = L

Definisi 2.1.9 (Ketaksamaan Holder )

xryt<ttrtlpttytte

= (I,',, ,)"* (t u,1'''

dimana p dan q adalah bilangan real yang lebih besar daripada I dan memenuhi _{p q}1+ 1= 1.

B. Diferensial Fungsi Kontinu

Dalam subbab ini akan dibahas mengenai limit, fungsi kontinu, barisan dan beberapa definisi-definisi dan teorema-teorema dasar tentang kalkulus.

Delinisi 2.2,1

Diberikan titikx € Rn dan d > 0. Kitar-d dari x didefinisikan sebagai

1 l

Definisi 2.2.2

Misalkan D c lRn dan x c D. Titik x disebut titik interior dari D jika terdapat suatu kitar-d dari x sedemikian hingga N6(x) c D.

Himpunan semua titik interior dari D disebut interior D dan dinotasikan dengan int(D). Selanjufiry4 jika int(D): D, yakni setiap titik dari D adalah titik interior dari D maka D adalahhimpunan terbuka.

Definisi 2.2.3

Diberikan fungsi f: E + R, E c R . Titik 16 disebut titik limit himpunan Ejika untuk setiap kitar dari rs momuat paling sedikit satu titik x € E danr =* xo. xs adalahtitiklimitE <+ (Vd > 0)(3 r e E)(0 < lr - xol < d).

Definisi 2.2.4

Diberikan fungsi f :E -> R, E c [R dan c € lR titik limit E. BilanganZ dikatakan limit /(x) untuk r mendekati c, jrkauntuk setiap e ) 0 yang diberikan, terdapat d > 0sehinggauntuksetiap x eE dengan0<lr-cl < d'maka

l f ( x ) - L l < e .

Definisi 2.2.5

Jika /(r) adalah sebuah firngsi real, maka limit /(r) untuk x mendekati tak hingga adalah l, dinyatakan dengan

t2

jika dan hanya jika untuk setiap e ) 0 terdapat bilangan .S > 0 sehingga untuk setiap x ) S berlaku lf (x) - Ll < e.

De{inisi 2.2.6

Diberikan fungsi .fr IR" -+ IR. Fungsi/dikatakan kontinu di X € IRU , jika untuk setiap e ) 0, terdapat d > 0 sedemikian hingga lx - fl < d' sehingga

l / ( x ) * f ( r ) l < e .

Selanjufrrya flrngsi / dikatakan kontinu pada IRn jl/ra f kontinu di setiap titik anggota IRz.

Definisi 2.2.7

Barisan {s"} dikatakan konvergen jika terdapat s € lR. dengan sifat, untuk sebarang e )0 yang diberikan, terdapat N€N sehingga untuk semua n€N dengan n >N berlaku ls - sr,l < e. Bilangan s dinamakan limit {s"} untuk n+ @ dan difulis lim4--sn atau disingkat limsr, = s. Suafu barisan yang tidak mempunyai limit disebut divergen.

Definisi 2.2.8

t 3

Definisi 2.2.9

Sebuah barisan vellor {xr} dikatakan konvergen ke x. jika I i m p - ' - l l x l r - x . l l = 0

Delinisi 2.2.10

Sebuah fungsi kontinu ,f: IR" + lR, dikatakan terdiferensial secara kontinu pada x € IRn, jika @f /Axi)(x) ada dan kontinu" i = t, ...,n,makagradient dari / di x ($adl)didefinisikan sebagai

vf (x):

#r*>

fft*>

fft*>

Q.2.1)

Gradien untuk fungsi multivariabel analog dengan derivative untuk fungsi satu variabel. Frrngsi multivariabel yang terdiferensial secara kontinu dapat memiliki minimum di x hanya ketika gradiennya bernilai nol.

Delinisi 2.2.11

t4

vzf (xlti =

#rrar,,

atau dapat juga didefinisikan sebagai

1 < 7 , , j 5-n. _Q.2.2)

/ ozf azf

t

-&

a4a.,

I arf Azf

V'f(x) :l o'.a*' &

t : :

I u"r azf \ar"arr aha-,

azf dr10xn

a2f

axA

Teorema 2.2.12 ( Teorema Nilai Rata-Rata )

Jika f kontinu pada selang tertutup [a,b] dan terdiferensial dalam interval ( a, b), maka terdapat paling sedikit satu bilangan c dalam ( q b) dimana

f(b) - f(aj

= f'(c)

b - a Q.2.3)

atau ekivalen dengan

f @)-f (a):f '(c) O-a) Q.2.4)

Bukti:

Pembuktian ini didasarkan _{pada analisis dari fungsi s(r) : f (x)-g(x), yang}

t 5

Gambar 2.2.1 (I earema Nilai Rata-rata)

Di sini y : g(tc) adalah persamaan _{garis yang melalui (a, f (a)) dan (b, /(b)).} Karena garis ini mempunyai kemiringan

tf &) - f (a)ll@-a) dan melalui (a,f (a)), bentuk titik kemiringan persam&mnya adalah

f(b) - f(a) .

g ( x ) - f ( a ) : ' t r @ - a )

Kemudian menghasilkan nrmus untuk s(x), yakni

s ( x ) = f(x)-f{a}-T

@ - a )

Perhatikan bahwa s(b) = s(o) = 0 dan bahwa gntuk x datam (ab)

s'(r) = f'(x) -f

(Q- f @)

_{b - a}

Jika diketahui bahwa terdapat suatu bilangmr c dalarn (ab) yang memenuhi s'(c) - 0, bukti selesai. Karena persanuun terakhir mengatakan

t 6

Untuk melihat bahwa s'(c) = 0 untuk suatu c datam (4b), alasannya adalah jelas s kontinu pada [ab], karena merupakan selisih dua fungsi kontinu.

Jadi menurut Teorema Eksistensi Maksimum-Minimum ( Jika / kontinu pada interval tertutup [ab], maka/mencapai nilai maksimum dan minimum), s harus mencapai _{nilai maksimum ataupun nilai minimum pada [a,b]. Jika kedua nilai ini} kebetulan nol, maka s(x) secara identik adalah nol pada [a,b], akibatnya s'(r) = 0 untuk semrra x dalam (a,b). Jika salah satu nilai maksimum atau nilai minimum berlainan dengan 0, maka nilai tesebut dicapai pada sebuah titik dalam c, karena s(a) = s(b) - 0. Sekarang ,s mempunyai turunan di setiap titik dari

(a,b), sehingga s'(c) = g. r

Teorema 2.2.13 ( Teorema Fundamental Kalkulus )

Andaikan / kontinu pada interval tertutup [a"b] dan andaikan F sebarang anti turunan darrf pada [ab] maka

b

f (x)dx = F(b) - F(a).

Bukti:

Misalkan didefinisikanG(x) : II f (i)af untuk setiap xo a S x 1 b, maka G adalah antiturunan daxr f pada [ab].

Karena F dan G adalah antiturunan dar: f pada [ab], maka ada sebarang konstantaCsedemikianhingga G(x) = F(x) +C untuk a<x 1b.

t 7

sehingga

II fUla, = f 71t1at

= G(b) = F(b) + c

- F(b) - F(a).

Teorema 2.2.14 ( Teorema Taylor )

Jika f adalah fungsi yang didefinisikan pada interval terbuka (b - r,b + r), 0 < r 4 oo, dan turunan yang ke n+l adadan semua kontinu pada interval. Maka untuk semna bilangan x di (b - r,b + r),

f (x)

- f(b)

+ f' (b)(x

- b)

+'ry+

...

+ try

f Rr,(r),

dimana

Bukti:

Dengan teorema Fundamental kalkulus dapat ditulis sebagai

p x

I f'(t) dt -- f (x) - f (b)

J b

atau

f (x) - f (b) + f'f'G) ar.

_J6

Q.z.s)

Dari persamaanQ.2.5) dimisalkan bahwa _{u = f '(t),du = f "(t) dt, dv = dt,} dan v - f - x, dimana r adalah sebuah konstanta pada variabel r.

f x I r l t x

l, f' {t)

41

- lf' (txt - r) - J $ - x)f" (t) dtllo

R'o,)

=

1 8

= f'(x)(x - x) - f'(b)(b - x) - I,Itt - x)f"(t)dt

: g - f' (b)(b - x) * I:(t - x)f" (t)dt

-- f ' (b)(x - b) - Il ft - x) f " (t)dt

Jika disubstistusikan hasil ini pada(2.2.5), diperoleh

f (x) -- f (b) + lX f'G) at.

= f (b) + f '(b)(x * b) - I;(t - x)f "(t) dt.

= f (b)+ f'(b)(x-b) + IXf*-t)f"(t) dt.

(2.2.6)

Dari persamaan (2.2.6), dimisalkan _{u -- f " (t),d'u = f "'(t) dt,} dv = (x - t)dt, dan v = -i(x - t)',diperoleh

r x

. : l r , , , r r f - q : - t Y l - f -(.-t)'

l l '

J o @ - t ) f "

( t ) d t = V " G ) t - ,

J I

z - f " ' ( t ) o r l l ,

= f,,(x){-ry}- f,,(b)t-ry}

- $ -@.y,,7t)

dt

= o * f,,(b)W\+ I;ryf,',(t) dt.

= f"(b)ry+

I ; r y f " ' ( t )

d t .

Jika hasil ini disubstitusikan pada(2.2.6) maka diperoleh

f (x) = f (b) + f'(b)(x - b) + I:@ - t)f"(t) dt.

f ( x ) _ f ( b ) + f , ( b ) ( x _ b ) + , r y + I : + f , , , ( t ) d t . Q . 2 . 7 )

1 9

f (x) = f(b) + f' (b)(x- b) +

f" (b)E:'- b)'

_{2 !}

+ ... +

f(n) (b)(x - Dn

_{n t}

F R r(r),

dimana

Rn(x)

-- filit* - t)nf(n+L)(t)

dt.

Teorema 2.2.15 ( Teorema Taylor di R?l )

Misalkan.f, lR" + lR terdiferensial secara kontinu dan bahwa p € Rt, maka

f (x+ p) = /(x) + V/(x + rp)"p

Q.2.8)

untuksuatuf

e (0,1).

Lebih lanjut, jika / terdiferensial dua kali secara kontinq maka diperoleh

vf (x* p) = v/(x) + liv'f (x + tp)p dt

Q.2.s)

dan

f (x+ p) - ,f(x) + +v/(x)rv +|prvzf (x+ rp)rp

(2.2.10)

untuk

t e (0,1).

Bukti:

Akan dibuktikan untuk"f yang terdiferensial secara kontinu.

Misalkan ,fr lR" + IR terdiferensial secaf,a kontinu pada himpunan terbuka E c lR? Maka untuk x €, E dan p e Rt, turunan berarah dartf padax dengan *fr p, didefinisikan dengan

20

Pandang _{untuk 11 norm fungsi f(x) = llxllt.} Dari definisi persamaan (2.2.11) diperoleh bahwa

Dctxttr;ol=l'*w=!gw

Jikaxi ) 0, diperoleh lr; * epil = lril * epiuntuk semua e yangcukup kecil. Jika x; ( 0, diperoleh

l - t , + r p , l = l - ( x i - e p ) l - l - l l l x ; - e p i l = l x i l - e p r

Jika :r1 = 0, lrr * epl = l0 + epi = elpil. Selanjutnya diperoleh Iip,tolri * epil -Ztgr>olxil

D(llxltr;

p) :

LS

, ,._ Xilr,.olxi * epil - Xilr,.olril +llm

, ,.- Xi1r,=olxi * eqi - Xilr,=6lrsl

T r l l l r

_ ,:* Xt1r,>olril * Xilr,to ePt - Xtlr,tolxil

= llfll .

-*r.* Xilr,<olri | - Xilr,<o €pi - Xilr,<olrr | * Hm Ztlr,=oelpil

€-t0 e 6+0 e

- el,rlrpoPd _{, ,.- -€Xilxi<oPi , ,,-elir4i=o?t} - lim --'-'- -' " * lim

e-r0 e €-r0 € e--+O e

r v r

=

/-t Lt Lt

ilri>o ilx;<o ilx;=s

Jadi turunan berarah dari fungsi f (x) adauntuk sebarang x dan p.

2 l

Untuk membuktikan formula ini, didefinisikan fungsi

Q @ ) - f ( x + a P ) = f ( v @ ) )

dimana (V(")) = x * ap. Catztbahwa

f(x + Ep) - /(x)

0(e) - 0(o)

l i m - = l i 1 n - = 0 ' ( 0 )

e+0 e e+0 e

dengan menggunakan _{aturan rantai pada f St@)) diperoleh}

Q'@)

=ry.#.rw.*.

..

+afggp)

#.

. af (y(")) dyn ' a y " ' d "

$ a1(vra))

- - L f f ' v Y i ( a )

i = L

=

t ry.Pi

= vf (v{o}}'P

: v/(x

+ ap)rp.

Dengan menggunakan q, = 0, diperoleh bahwa

0'(0) - v/(x)rp - D(/(x); p).

Dengan menggunakan Teorema Nilai Rata-rata. Misalkan diberikan sebuah

fungsi yang terdiferensial secara kontinu @: lR -+ IR dan terdapat paling sedikit

satu bilangan { dalam (qo,at), dimana 40 = 0, dt = 1- diperoleh

22

Jika a diganti menjadi a1 maka

Q@) = f (x* arp) Q.2.r2)

Substitusikmrdt = l" ke dalam persamaan _{Q.2.12) maka diperoleh} d(1) = /(x + p).f*a a diganti menjadi as maka

Q@i = .f(x * aop) Q.2.r3)

Substitusikan do = 0 ke dalam persamaao _{Q.2.13) maka diperoleh 0(0) = /(x).} Suatu perluasan _{dari hasil ini untuk fungsi multivariabel f: Rz + R. bahwa untuk} sebarang vektor p diperoleh batrwa

f (x + p) = f(x) + V/(x * ap)rp

untuk suatu a € (0,1). Jadi terbukti untuk/ yang terdiferensial secara kontinu. Selanjutnya untuk bukti / yang terdiferensial dua kali secara kontinu analog dengan bukti/ yang terdiferensial secara kontinu di atas. r

Definisi 2.2.16

Jika /: lRn + IRm terdiferensial kontinu dalam terbuka D c IR?, maka untuk setiap &x + d e D, diperoleh

f (x+ d) - f(x) = [i f g+ rd)d

o, = f*u/'(€)dq.

e.z.r4)

Definisi 2.2.17

23

Teorema 2.2.18

Misalkan,f . IR" -+ IRm terdiferensial kontinu dalam terbuka D c IRn. Misalkan /'kontinu Lipschitz di x e D. Maka untuk suatu x + d € D, diperoleh

Q.2.rs)

s Ilylladlllldllda

= zlldllz

I] " a"

=

; ildilr.

C. Masalah Optimasi

Secara umum optimasi merupakan tindakan untuk mendapatkan hasil yang terbaik terhadap situasi yang diberikan sebagai suatu masalatr. Optimasi dapat didefinisikan sebagai proses mencari atau menemukan situasi yang memberikan nilai maksimum atau minimum dari suatu fungsi. Secara matematis optimasi merupakan proses menemukan nilai maksimum atau minimum dari suafu fungsi dengan cata memaksimalkan atau meminimalkan fungsi tersebut. Untuk

llfC*

+ d) - /(x) - /'(*)dll < | ilalt'.

Bukti:

/(x + d) - f(x) - f'(x)d = lo" f't*+ ad)d da - f'(x)d

f l

=

Jo

[/'{* + ad) - f'(x)]d da.

Jadi

llfC*

+ d) - /(x) - t'(*)dll = fllf't* + cd) - f'(*)ll lldltda

24

menentukan penyelesaian masalah optimasi dalam bentuk maksimum fungsi, ekuivalen dengan menentukan minimum dari negatif fungsi f ( -f ) atau dapat dinyatakan sebagai min ( -/).

Secara umum masalah optimasi dibagi menjadi dua bagian, yaitu masalah optimasi dengan kendala dan masalah optimasi tanpa kendala.

1. Bentuk umum masalah optimasi dengan kendala. min f(x)

x€lRn' - '

dengan kendala c i ( x ) = g ' i € t

atau c i ( x ) > 0 , i € 9 . Dengan:

"f(x) = fungsi obyektif

t = himpunan indeks dari kendala yang berupa persama:ul t = himpunan indeks dari kendala berupa pertidaksamaan 2. Bentuk umum masalah optimasi tanpa kendala.

25

D. Optimasi Tanpa Kendala Definisi 2.4.1

Misalkanfix) adalah fungsi bernilai real yang terdefinisi pada himpunan bagran D di IRn. Titikx* e D adalah:

a. Peminimal global untuk{x) paila D jika,f (x.) < /(x) untuk setiap x € D. b. Peminimal global tegas untuk{x) pada D jtka,f(x.) < /(x) untuk setiap

x € D sedemikianhinggax # x'.

c. Peminimal lokal untuk/(x) jika terdapat suatu bilangan positif d sedemikian hinggaf(x.) </(x)unhrksetiapx€ D dimanallx-x.ll < d.

d. Peminirnal lokal tegas untuk Xx) jika terdapat suatu bilangan positif 6 sedemikian _{hingga f(x-) </(x) untuk setiap x €D dimanallx-x.ll < d} dan x * x*.

e. Titik kritis untuk /(x) jika turunan parsial pertama dari"f (x) ada di x'dan

5 ( * - ) = 0 ,

i = \ , 2 , . . . , T t .

oxt

fisilrmininal lokal rqu t

I '

' 'rJ .r" lPerninirnd lakal p.ildr'lnal _dobal-,,

\*-

\. i \ n

*.rr'

H \ t , /

26

Definisi 2.4.2

Misalkan/: lRl + lR. terdiferensial pada x € lRn. Jika ada sebuah vektor d e Rn sedemikian hingga (V/ (x),d) < 0, maka d merupakan arah turun (descent direction) dari/di x.

Dengan menggunakan ekspansi Taylor,

.f(xr + td) : /(xr) + tvf (xp)rd + o1t), maka

ld > 0sedemikianhingga.f(xr+td) < f(x),vt € (0,d)

jika dan hanya jika d adalah sebuah arah turun (descent direction) dari/di x.

Teorema 2.4.3 (Syarat Perlu Tingkat Pertama)

Misalkan/ : D c lRa + IR terdiferensial secara kontinu pada himpunan terbuka D. Jikax* € D adalahpeminimal lokal/(x) maka V/(x.) = g.

Bukti:

Akan dibuktikan dengan kontradiksi. Andaikan bahwa V/(x.) + 0.

Ambil a = -Vf(x*) sehingga diperoleh _{drvl(x.) = -llv/(x.)llz < 0, maka} d adalah arah turun (descent direction) dan ada d > 0 sedemikian hinggu f (x. * ad)< .f(x.), Va € (0,d). Hal ini kontradiksi dengan asumsi bahwa x* adalah peminimal lokal.

27

Teorema 2.4.4 (Syarat Perlu Tingkat Kedua)

Jika x* adalah peminimal local danf danYz f ada dan kontinu pada sebuah kitar terbuka dari x*, maka V,f(x.) = 0 dan V2f (x.) adalah semidefinit positif, Bukti:

Akan dibuktikan dengan kontadiksi.

Andaikan Vzf(x.) bukan semidefinit positif, maka dapat dipilih d€lR?r sedemikian _{hingga drV2 f (x.)d < 0 dan karena V2l kontinu dekat x*, ada}

d > 0, dapat dipilih e ) 0 sedemikian hingga drvz1(x. + ed)d < 0, wrhrk s e m u a € € [ 0 , d ] .

Dengan menggunakan V,f(x.) = 0, dari persam&m _{Q.2.12) dapat dihasilkan} ,f(x. + ed) =,f(x.) +)ezarvrf (*. * ded)d,

dimana0 < 0 ( 1,maka _{f(x. + ed) <,f(x-).}

Hal ini kontradiksi dengan asumsi bahwa x. adalah peminimal lokal.

Jadi pengandaian salah, haruslah V'f (*.) semidefinit positif. r

28

E. Metode Newton

Metode Newton adalah salah satu metode untuk menyelesaikan sistem persamaan nonlinear. Secara umum metode ini digunakan untrk menyelesaikan sistem persam&ul

g ( x ) : 0 ,

dimana gi(x) fungsi diferensiabel pada IR? dengan nilai fungsi dalam lRn, i = 'l-, ...,n.

Metode Newton adalah suatu algoriftna iterasi fungsional yang menghitung xk = xk-1 - I(xr.-r)-1F(xr-r) dengan fr > I dan J(x) adalah matriks Jacobi dari sistem persamaan non-linear, yakni

I(x) =

1xt ilxz }xn

0fz8) afzF)

lfzg)

dh. ilxz |xn

lxt dxz |xn

Teorema 2.5.1

Misalkan [xr] adalah barisan metode Newton untuk meminimumkan suatu fungsi/(x) . Jtka Hf (xy.) matriks Hessian dari"f(x) di xl,adalatr definit positif dan jika V/(x;,) + 0, maka arah

29

dari x6 ke x;, * 1 merupakan arah turun/(x) dalam arti terdapat suatu e) 0 sedemikianhingga _{f (x*+ tpr) < f(xr)}

uqtuk semua t sehingga 0 < t < e. Bukti:

Definisikan q(t) =.f(xr + tpr).

cp(t) adalahbatas dari/(x) untuk melewati xr pada arah dari pp maka q ' ( t ) = v f ( x r * t p J ' p H

dan

q'(o):

i::rlro-r-1v/(xk) < o,

karena [H/(xr)]-1 adalah definit positif dan Vf(x ) + O. Sehingg4 ada e ) 0 sehingga gG) < g(0) untuksemua/dimana0<t<e, bahwa

, f ( x r + t p r ) < / ( x r )

30

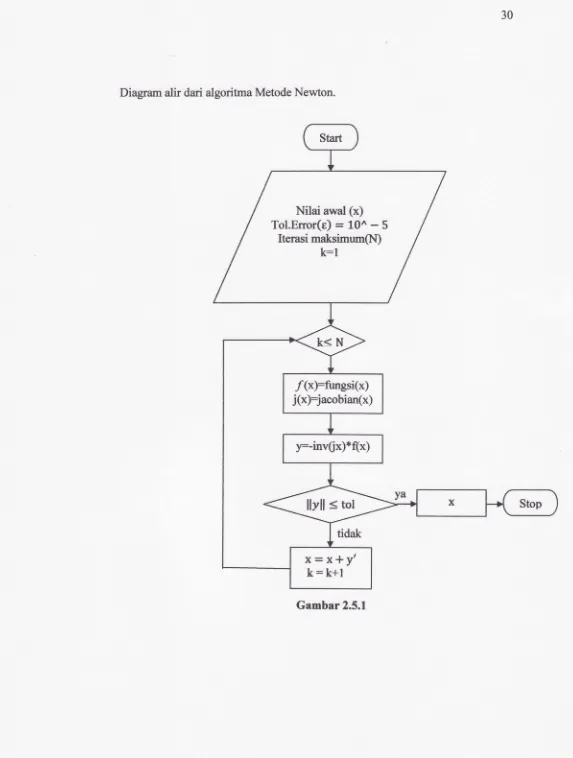
Diagram atir dari algoritma Metode Newton.

Gambar 2.5.1 Nilai avnat (x) T o l 3 r r o r ( e ) = 1 0 ^ - 5

Iterasi maksimtm(N) FI

/(xfftngsi(x) j(x):jrcobian(x)

BAB III

METODE DAERAH KEPERCAYAAI\ T]NTT]K MEITYELESAIKAI\I MASALAH

OPTIMASI TAITPA KENDALA

A. Metode l)aerah Kepercayaan

Metode Daerah Kepercayaan merupakan salah satu metode yang digunakan untuk menyelesaikan masalah optimasi. Pada penulisan skripsi ini, masalah yang akan diselesaikan hanya terbatas pada masalah optimasi tanpa kendala, dengan bentuk umum

min/(x) untuksetiapx€lRn.

Metode ini membangun langkah dengan bantuan fungsi model mr yffir1 berbentuk kuadratik untuk menghampiri fungsi objektif/dan mendefinisikan suatu daerah di sekitar iterasi yang sedang berlangsung yang dipercayai bahwa model tersebut akan meqiadi representasi yang baik dari fungsi objektif

Strategi dalam Metode Daerah Kepercayaan adalatr mendefinisikan suatu daerah yang disebut daerah kepercayaan, _{yaitu Or = {xl llx-xrll S Ar},} dengan A1, sebagai jari-jari daerah kepercayaan op, kemudian memilih sebuah langkah yang menjadi peminimal hampiran dari model m* yang

32

berbentuk kuadratik. Langkah ini diharapkan menjadikan x semakin mendekati peminimal dari fungsi objektif. Llkuran langkah ini kurang dari atau sama dengan Ap. Pengoptimalan dari model ini dapat dilakukan dengan memeriksa setiap x € IRT! yang meminimalkan nilai/(x). Jika langkah ini tidak menghasilkan penurunan nilai fungsi objektif, maka ukuran jatak Ap akan dikurangi dan selanjutnya car.a yang sama diulang kembali untuk mencari penunrnan nilai fungsi objektif yang lebih baik. Dalam metode ini, fungsi objektif/digunakan untuk membangun firngsi model mn yffiE sifanrya sama dengan fungsi objektif / di daerah sekitar x. Karena model m1, tidak bisa meqiadi pendekatan yang baik untuk"f bila x jauh dari xp maka ukuran daerah kepercayaan akan dikurangi dan mencari peminimal baru di sekitar x;, € IR?. Fungsi model mp didasarkan pada ekspansi deret Taylor di sekitar xp,yaitu

f (xn + p) = fi,+ gkrp +)vrv2f(xr, * rp)p + o0pll2)

(3.r.r)

diman4 p: besar langkalL _{h="f (*) dan gr: Vf(xu), untuk t € (0, l).}

Dengan menggunakan matriks .B1 sebagai pendekatan matriks Hessian di dalam syarat orde kedu4 maka mpdapx didefinisikan sebagai

J J

Untuk memperoleh setiap langkah, dicari solusi dari

fffo**u(n)

= f*+ glp +)vrB*v

I

l (3. 1 .3) dengan llpll < Ar )

dimana Ar > 0 adalah jari-jari daerah kepercayaan. Peminimal darimp dalam bola yang berjari-jari Ap adalah pi yang diperoleh dengan menyelesaikan masalah pada persamaan (3.1.3).

Untuk menyelesaikan masalah optimasi dengan hampiran daerah kepercayaan diperlukan penyelesaian barisan submasalah dari persamaan (3.1.3), dimana fungsi objektif dan batasannya berbentuk kuadratik, yakni dapat ditulis sebagai prp S Al. AiU Bradalah matriks definit positif dan llB;Lgrll S Ar, berdasarkan teorema (2.5.1) maka solusi dari masalah (3.1.3) adalah

p7'- = -Bi1gp yakni peminimal tanpa kendala dari fungsi model kuadratik m*(p). Dalam kasus itti, pf, disebut langkah penuh.

Salah satu kunci penting di dalam metode daerah kepercayaan adalah pemilihan Ar yang tepat untuk setiap iterasi. Pemilihan ini didasarkan pada ke sesuaian antar a model m p dengan fu n gsi obj ektif.

Diberikan sebuah langkah p1, didefinisikan sebuah rasio atau perbandingan

, f ( x r ) - f ( x * + p r )

(3.1.4)

Pt< = _{mn(A) - mr(pn)}

34

memr#$ P : 0, penurunan yang memainkan peranan yang penting

diprediksi akan selalu nonnegatif. dalam pemilihan iterasi yang baru

memperbaiki jari-jari daerah kepercayaan Ar. Jika p* negatif, maka nilai

fungsi objektif yang baru f (xn + pe) lebih besar daripada nilai /(xp), sehingga langkah ini dibatalkan. Jika pr dekat dengan satu" ada kesesuaian antara fungsi model m1, dengan fungsi objektif/pada langkah ini, sehingga pada iterasi berikutnya daerah kepercayaan dapat diperluas. Daerah kepercayaan dapat diperluas karena model yang terbentuk memberikan hasil yang hampir sama dengan fungsi objektif/ Jika prpositif, namun kurang dari satu, daerah kepercayaan tidak diubah, karena model untuk memprediksi belum menghasilkan nilai-nilai yang dekat dengan fungsi objektif/sehingga akan mencari p yang baru tetapi jika dekat dengan nol atau negatif, daerah kepercayaan diperkecil dengan mengurangijari-jari kepercayaan pada iterasi berikutrya karena selisih f (x*) dan /(xr + pr) terlalu kecil sedangkan selisih mrc(O) danmp(pp) besar. Jadi, model yang dibuat tidak sesuai dengan firngsi yang sebenarnya. Karena pada model terjadi penunrnan nilai fungsi yang besar tetapi pada fungsi yang sebenarnya penunrnan nilai fungsi hanya sedikit.

pk

35

B. Algoritma Metode llaerah Kepercayaan

Melalui teorema berikut ini, akan diberikan solusi dari solusi masalah (3.1.3). Untuk itu, indeks k yarrg ada dalam persama:m (3.1.3) dihilangkan dan kembali dinyatakan sebagai

p5*m(n)

=f +srr+LrP'rP

(3.2.r)

dengan llpll < A

Lemma 3.2.1

Misalkan m fungsi kuadrat yang didefrnisikan dengan

m(p) = grp + f,pr Bp, Q.2.2)

dimana B adalahmatriks simetrik dan pernyataan berikut adalah benar. ( i ) m mencapai minimal jika dan hanya jika B semidefinit positif dan g

berada dalam range B.

Jika B semidefinit positif, maka setiap p memenuhi Bp = - g adalah peminimal global untuk m.

( ii ) m memiliki sebuah peminimal tunggal jika dan hanya jika B definit positif.

Bukti: ( i ) ( < : )

B adalah matriks semidefinit positif.

36

Perhatikan bahwa:

Vm(p) - Bp * g, jika Vm(p):0 diperoleh Bp = -9. Karena g berada dalam range B maka ada p dengan Bp = -g Untuk setiap w € lR?, diperoleh

m(p +w) - g"(p + w) + i Cp * w)rB(p + w)

-- grp + grw +f,vr Bv +|vr aw +|wr np +) wr nw

= (tto + |o' nv)+ s'w + (prBw +|wr np1 +| wr nw

Perhatikan

bahwa: LrV'a* +|wr np = (Bp)rw

:

)to'n.'.D'

*}(w'trp)'

: f,{n'n'p)r

+ f,{v'n'."D'

karena B matriks simetrik maka Br: B sehingga diperoleh

:

f,{n'nil +}orrw)

dengan

kata

lain |{-"rn) =}{v' n*)

Jadi, |{*trn) + }{*t"rn)

=

f,{nil'",+l(Bp)'w

= (Bp)rw

Jadi terbukti bahwa _|V'n* +|w'Ap = (Bp)rw

37

= m(p) + gtw + (-g)tw +| wr aw = m(P) + f,wr nw

> m(p) (3.2.3)

Karena B matriks semidefinit positif maka wrBw ) 0,Vw € IRn sehingga |wrBw > 0.

Dari m(p + w) > m(p) terbukti bahwa m mencapai minimal dengan peminimal p, karena Vw c lR", m(p) < m(p + w).

(:>)

Misalkan p peminimal untuk m.

Akan ditunjukkan B semidefinit positif. m(p) = grp +)erBV

Perhatikan karena p peminimal untuk mmaka Vm(p) = 0, yakni V m ( P ) = B P * g = 0

Sehingga Bp = -g. Disimpulkan bahwa g berada dalam range B. Perhatikan juga Vzm(P) = B. Karena B adalah matriks simetrik pada fungsi m(p) dan nilai V'm(p) ada maka menurut teorema syarat perlu tingkat kedua Y2m(p) = B semidefinit positif.

( i i ) ( < : )

38

B adalah matriks simetrik yang definit positif maka wrBw > 0, V w € l R n , w l 0 .

Untuk setiap w € IRn, diperoleh

m ( p + w ) - g r ( p + w ) + i t p * w ) r B ( p + w )

= grp + gtw + |vr Bv +|vr nw +f,wr np +| wr aw

: (tto + inran) + srw + (Bp)rw + f, wr nw

: m(p) + grw + (-g)rw +) w'nw

: m(p) + f,wr Bw

> m(p)

Jadi p adalahpeminimal global untukm. Jadim memiliki peminimal tunggal. (:>)

Misalkan m memiliki peminimal tunggal akan ditunjukkan B matriks simetrik yang definit positif.

Bukti dengan kontradiksi

B bukan matiks simetrik yang definit positif maka ada vektor w + 0 sehingga Bw = 0.

Sehingga

m(p +w) - sr(p + w) + i tp * w)rB(p + w)

39

: (tto + intan) + s'w + (BP)rw + ] w'rw

m(p) + g?w + (-g)rw +)wr nw

: m(P) +!;wrBw

m(p) + iwr(o;

Jadi m(p * w) : m(p)

Jadi peminimal m tidak tunggal.

Jadi pengandaian bahwa B bukan matriks simetrik yang definit positif

salah. I

Teorema 3.2.2

Vektor p. adalah penyelesaian global dari masalah daerah kepercayaan

Sft*-(n)=f+srp+|{ao

}

,3.2.4)

denganlfpil<a

]

jika dan hanyajika p- adalah penyelesaian layak dan ada suatu skalar 1>0 yang memenuhi kondisi:

(B+ LI)p* = -g

I(A- llp.ll)

- o,

(B + 1I) adalah semidefinit positif Bukti :

( < : )

Diasumsikan bahwa ada 1> 0 sedemikian hingga

(3.2.sa)

(3.2.sb)

40

(B + uI)P' = -g

)

I ( A - l f P . [ l ) = o

]

( 3 . 2 . s )

(B + 1I) adalah semidefinit posidf) terpenuhi.

Akan ditu{ukkan p*peminimal global dari masalah daerah kepercayaan

miqm(p)

= f +s"p + )f nv

I

p e R ' - z - - l

d e n g a n l l p l l < A ₎

Perhatikan persam&n (3.2.2), dengan mengganti matriks B dengan B + 1l maka peminimal fi(p) = grp + ivr (B + il)p.

Dari lemma 3.2.1(i) dan bahwa (B + 1I) adalah semidefinit positif maka fi mencapai minimal dengan _{peminimal fi. adalah p. ( peminimal global ).}

Perhatikan

n(p)

:1, .rJ::::,

m(p) + lvro

Q.2.6)

karena p. adalah peminimal global untuk fi maka n(p) 2 fi(p.) atau

n(p) = m(p)

+lvrv2 m(p.)

+X(p.)rp.

= fi(p.)

m(p))m(p.)+J{{n.)tp.-prp)

(3.2.7)

karena 1(A - llp.ll) = 0 maka l(Lz - (p.)tp.) = 0,sehingga diperoleh ( a 2 - ( P . ) r P . ) = o

atau 42= (p*)"p*

4 l

jadi, dari l, > 0 diperoleh m(p) > m(p.)untuk setiap p dengan llpll S a. Jadi, p* adalahpeminimal global darr(3.2.4)

(:>)

Diasumsikan bahwa p. adalah penyelesaian global dari

min m(p) -- f + srp + in'rn

)

d e n g a n l l p l l < A ₎ Akan dibuktikan bahwa adal> 0 yang memenuhi (3.2.5) a.) Untuk llp-ll S A, p* adalah peminimal tanpa kendala darim.

Perhatikanbahwa m(p.): f + grp. **(p.)rBp. maka Vm(p.) -- Bp* * g = 0

sehingga Vzm(p.) = B semidefinit positif

maka akan ditunjukkan sifat-sifat (3.2.5) berlaku untuk ).= 0. Akan ditunjukkan 1)"> 0 yang memenuhi (3.2.5a)

Perhatikan (B+ LI)p* = -g B P . * J L P * = - E B p . * g * i p . - 0

karena Bp* + g = 0 maka persamaan di atas menjadi 0 + ' L P * = g

i P * = o

42

karena _{llp.ll < A maka A - llp.ll > 0}

supaya _{i.(A - llp.ll) = 0 maka} haruslah,t : 0.

Akan ditunjukkan 3 2 > 0 yang memenuhi (3.2.5c)

Karena.B semidefinit positif supaya (B + 1I) semidefinit positif maka )": 0.

b.) Untuk llp.ll = A maka (3.2.5b) berlaku.

l(L- llP.ll) : 0

karenaA= llp.llmaka (A - llp.ll) = 0.

p. juga menyelesaikan masalah berkendala

min m(p) dengan _{llpll: A.}

Dengan menggunakan kondisi pengoptimalan untuk masalah optimasi

berkendala pada masalah ini, dapat ditemukan bahwa ada I dari fungsi

Lagrange yang didefinisikan oleh

L(P,l) = m(P) -|<o' - PrP)

L(P,I) = m(P)

+!@rn - Az)

Persamaan di atas memiliki titik stasioner di p..

vo.c(p.,r,)

= s + Lrn **,t, *|O * n>

p'sebagai titik stasioner maka

Vo,C(p.,l) - Bp* *g+lp* = 0 ==t (B + Ll)p. = -g (3.2.8)

43

karena m(p) 2 m(p.) dimana p. titik stasioner untuk sebarang p dengan prp = (p.)tp. = A2, p. adalah penyelesaian global.

Didapatkan untuk vektor p bahwa

fi(p) > fi(p.)

m(p)

+ lvrvt m(p.)

+ f {n.)"n.

m(p)

2 m(p.)

+ x((p.)rp.

- prp)

(3.2.s)

Jika mensubstitusikan pernyataan untuk g dari (3.2.8) ke dalam (3.2.9), akan diperoleh menjadi

m(p) 2 m(p.) + *(p.)rp. - * ptp

g"p * f,v'av2 gtp. +;o.)?Bp- +f,(p.)tp.

-*r'o

(-(B +.tr)p.)p

+|ornv > (-(B +.r/)p.)p.

+ j{n.)tBp*

+}{n.)tn.

-lp'p

p(-Bp. - ip.) +!v'nv ) p.(-Bp*

- rp*) +|{v)r ap-

+:(p.)"p.

-* ptp

-prBp* -iptp* +|v'Bv 2 -(p.)rBp. - r(p.)tp* +|{R.)tan- +

f{n.)tR.

-Lro'o

44

1

1{v'nv - ptBp. + ip'p- hp'g* - (p.)tBp+ (p.)tBp. -i(p.)tp + r(p.)tp* > 0

1

2{v'nv

+ lprp - (p.)tBp - i(p.)tp * p'Bp. * hp'p'+ (p.)rBp.

+ r(p.)"p* > 0

1

-7{$'n + up'- (p.)tr - t(p.)t)p - (p"g + tp' - (p.)tB

- i.(p.)r)p.] > o

1

1{v'n +

lp'- (p")"8

- i(p.)TG - p.) z o

ito-p.)'(B +Lr)(p-p.) )0

(3.2.10)

Karena himpunan arah

( p - p * _{, )}

{w

: w : tffip,

untuk

seiumlah

p dengan

llpil = nJ

memadati lingkaran satuan, (3.2.10) cukup untuk membuktikan (3.2.5c). Karena (3.2.5a) dan (3.2.5c) dipenuhi oleh p*, dan daxi Lemma 3.2.1 (i) diketahui bahwa p* adalah peminimal untuk fr maka

m(p) 2 m(p') *|{$.>rp. - prp)

berlaku.

Andaikan hanya terdapat nilai-nilai ,l y*g negatif, maka m(p) > m(p.) saat

l l p l l

> l l p . l l

= 4 .

45

Bp : -g (berlaku juga untuk p*) dan B semidefinit positif. Kondisi (3.2.5a), (B + LI)p* = -g

B p * +ip* = -g

Persamaan ini akan menjadi Bp* = -g bila 7p* = 0, dan p* * 0, maka nilai ,1. harus nol.

Terdapat kontradiksi, pengandaian salah.

Jadi, disimpulkanbahwa 1> 0. r

Berdasarkan keterangan di atas dan dari Definisi 2.4.1e dapat dibuat suatu algoritma berikut ini untuk menyelesaikan masalah daeratr kepercayaan.

Algoritma 3.2.1

Langkah 1. Diberikantitikawal xs, -L, _{A0 € (0,I), e 2 0,0 < It<421L} k : = 0 .

Langkah _{2. Jika llgrll < e, stop.} Langkah 3. Selesaikan masalah

igfu**n(d

= f*+ g[P +]orB*

denganllpll < Ar untuk mendapatkan pr. Langkah4. _{Hitung f (xn+ pk) danpr,}

Tentukan

X; _{l+1 -t} - lxn * P*' iika Px 2 rlr

46

Langkah _{5. (i) Jika pn l tlrmaka Ar+r= 4rAr}

(ii)Jilo Pr 2 ryz,maka Ap11=min (zLk, E) (iii) lainnYa Ar+r= Ar

Langkah 6. Hitung.Br+1, perbaharui tt416, Ltlur k:: k + 1, lanjutkan ke Langkah2.

Diagram alir dari algoritna Metode Daerah Kepercayaan

I

Nilai aw:al (x) E,A*,rl",rt, Tol.Error(e): 10^ - 5

Iterasi maksimum(N) lFl

/(xffingsi(D

47

llg(r)ll < e

pr = mll mrctp)

= fr, * *,p +|f a*o

peRn

X r + 1 : X r * P r

xk+l = x[

A*+t= ?tL*

Ap*.=min (2A*,Zj

L*+t: Lr

B*nt

fflp

k : k + l

48

Berdasarkan algoritna ini I adalah batas maksimal dari panjang langkah. Jad - jari daerah kepercayaan _{akan ditingkatkan hanya jika llprll mencapai} batas dari daerah kepercayaan. Jika langkah masih berada di dalam daerah kepercayaan, disimpulkan bahwa nilai Ar( saat ini tidak mempengaruhi kemajuan dari algoritma, jadi nilai itu tidak diubah untuk iterasi berikutrya. Iterasi dengan prc242 sehingga Ar*r2 Ap dikatakan iterasi yang sangat baik, iterasi dengan pn 2It sehingga _{xk+1 : xr * Pr dikatakan iterasi yang baik,} iterasi dengan pr 1It sehingga xk+1 = xp dikatakan iterasi yang tidak berhasil.

Contoh 3.2.1

Diberikan suatu fungsi /(x) = xl + zxlxl + xt. Dengan metode Daerah Kepercayaan akan dicari pembuat minimum dari fungsi tersebut.

Penyelesaian:

Untuk menyelesaikan masalah di atas, ikuti langkah-langkah dari algorifina metode Daerah Kepercayaan.

Iterasi 1 Langkah I

Inisialisasi i xo: (0, -1) A = 5 e = 10-s ao € (0,5)

Ao= 1

1

4 t : tr

3

49

Langkah 2

Hitung llgrll < e

/+xl + axaxl\

s(x) = v/(x) =

\+*ir, + iri )

u'= (jn)

sehinggallgoll

= J'tr+ f-qy=4)e

karena llsoll > e dilanjutkan ke langkah 3. Langkah 3

Hitung

B(x) - vrf (x) = (tz(

+ +x3

. ?'*.'- "\

" - \ 8 x 1 x s 4 x l + 7 2 x l J

t, = (fi ,:r)

mr(p) = f(x) +g(x)rp+|prB(x)n

= xt + zxlxl + xt + (axl + 4xpl)p1+ (4xlx2 + 4xl)p2

| .

o,\(Lzr?

+ 4xl

Bx7x2 \ fpr.

+)ra, --,

\ 8x1x2 nri|-irill;)

= xt + 2x21x22

+ x! + @xl + 4xpl)p1+ (4xlx, + axl)p,

*)fOr*? + 4xllp1* {8xp2}p2 {8x62}pt + {+xl + tzrilprl) (ft)

= xt + zxlxl + xt + Uxl + 4xpf)p1+ (4xlx2 + 4x|)p2

1

+lttzx? + axllpl + (*xrx2)?zpt*

(8x:r2)pp2

50

= xl + zxlxl + xt + @xl + 4xpl)p1+ (4xlx2 + xlJp,

+(6x? + zxl)pl * (8xp)ptpz * Qxl + 6x)p3

Cd po dengan meminimumkan 116

nlo = o4 + 27012(*Dz + (*1)4 + (4(0)3 + 4(0X-1)')p"

+(4(0)2(-1) + 4(-r.)')p, + (6(0)2 + z(L)2)pl

+ (8(ox-t))ppz + (2(0)2

+ 6(t)2)pl

: 0 * 0 + l + 0 - 4 p r + 2 p ? + 6 p Z

- l - 4 p z * z p l + 0 p 2 ,

vmo(po)

= (_rTirr,)= (3)

? t = 0

- 4 + L 2 p 2 - O L2p2 - 4

1

? , = ;

Langkah 4

,f(xo) = f (0,-1) = 04 +Z(O)2(-1)2 * (-1)a = 1

.f(xo

+ po)

= r (0,-r3)

= o' + z(0)z(-;)' * (-i)- = H

mo(O) - ! -4(0) + 2@)z * 6(0)2 = 1

mo(po)

= | - n(*)

* z@)'*

u(i)' : r - i*'t=i

5 l

Sehingga berdasarkan persrLmaan (3.1.4) maka

o , = H = ? = { r * t z o +

Karena po 2 qtmaka x1 = Xs * ps

= (0,

-1) + (o,i)

= (0,-3)

Langkah 5

karena po 242 maka Ar= min (2Ao,I;, yakni At= 2. Langkah 6

_ (ns1z + 4(-3J'

B(o)

(-;) \

Hitung Br:l

\ s(o)

(-;)

4(o)'

+ n(-i)' )

:(+ o\

\o +l

maka

nt1 -- 04 + z(0)z

(-t)' * (- 3)- + (+101'

+ 4(0) (- ?)') o,

* (+col'

(-i) . * (-3)')p,

* (e101'

+ z(-'-)')e?

+ (sqov

(-3) PtPz

*(r,or' + o(-z)')r?

= o * o * # + o - # p , * i n i + ! v l

L 6 3 2 8 t 2 4 . t

32

Iterasi 2 Langkah 2 Hitung llsnll S e

sehingga _{llgrlf =}

= , 2 > e

_{2 7}

karena llglll > e , dilanjutkan ke langkah 3. Langkah 3

s(x)

= vf (x)

: (ifr;-:;:i)

n _(

ntor'+4(o)(-i)'

\

t' =

\n,o

), (-) + +1..'r7'

)

= (-'#)

v^,1p"1=(

,f';, )= (3l

\ _ , * T p r /

P t = 0

3 2 . 4 8

- ; + l P z = 0

2

P r = 6

/0\ J a d i , p l = l f l

53

Langkah 4

/(x,) = /(0,-?) = oq

+ z(o)2(-i)'

+ (- ?)r =#.

f (x"+pr)

= f (0,-i) = on

+ z@)z

(-;)'* (-;)- = #.

mr(o)

= #-fi fal + ! to)' +! fo>'

= "fi

m{p)=

#- #g+ !to)'

*+A' = e

Sehingga berdasarkan persamaan _{( 3. l. 4 ) maka}

o " = f f i = # = # " - L Z o 4

_-e1.-ffi

Tg

Karena h 2It maka x2 : x1 * p1

: (0,

-i) * (o,i)

: (0,-i)

Langkah 5

karena h) ez maka Az= min (2At,[ l,yatcni Az= 4. Langkah 6

Hitune

," =(t"o)'

-

+ n(-:)'

8(o) (-;)

\

\ s(o)

(-;)

4e),

+ n(-|)' I

/ o + O \ : ( *

s z l

s4

maka

*tz = 04

+ z(0)z

(-;)' + (- i)- * (u,or' + 4(0) (- i)')0,

+ (+10;'

(-i) * n (-il') v, + (es1'

+ z(-i)')v?

+ (ecol

(-;)) ptpz

*(r,or' + a(-)')vi

= o *

o * # + o - # o r + f t v ? + f i v ?

2 5 5 2 5 6 . 3 2 t 3 2 I

:

Aa - Ts?z + uPi + VPi Iterasi 3

Langkah 2 Hitung llsnll S e

s(x)

= vf

(x)

= (ifr;f;:l)

_ ( n t > ' + 4 ( o ) ( - t J ' \

t ' =

\ n , o ) ' ( -

) + + 1 - g ' )

=(-k)

sehingga _{llgzll :}

_ r t a > ,

729

karena llg2ll > e lanjutkan ke langkah 3.

55

Berikut akan diberikan penyelesaian dengan menggunakan program MATLAB.

Tabel3.2.1 Output penyelesaian contoh 3.2.1 dengan Matlab

k I x(l) x(2) | p(1) I p(2) | (x) _{I norm(g(x))}

I 2 J 4 5 6 7 8 9 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 -0.66667 -0.44M4 -4.29$A

-0.r97s3

-0.13169 -0.08779 -0.05853 -0.03902 -0.02601 -0.01734 -0.011s6 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.33333 4.22222

0 . 1 4 8 1 5

0.09877 0.06s84 0.04390 0.02926 0.01951 0.01301 0.00867 0.00578 0.197s3 0.03902 0.00771 0.00152 0.00030 0.00006 0.00001 0.00000 0.00000 0.00000 0.00000

1 . 1 8 s 1 9

0.3stt7 0.10405 0.03083 0.00913 0.00271 0.00080 0.00024 0.00007 0.00002 0.00001 1 0 1 l

Pada saat iterasi _{ke-l1, llgrll < e}

56

C. Kekonvergenan Metode l)aerah Kepercayaan

Selanjutny4 untuk membuktikan kekonvergenan pada metode Daerah Kepercayaan akan diberikan beberapa asumsi dan lemma.

Asumsi 3.3.1

Diasumsikan matriks hampiran Hessian Bp terbatas seragam dalam norma, yakni llBrll < M, dinana M adalahsebuah konstanta _{positif dan f terbatas ke} bawah pada himpunan tingkat

{xlf (x) < /(xo)}.

(3.3.1)

Secara umum, panjang dari solusi hampiran pp dari (3.1.3) dapat melewati batas daerah kepercayaan, rurmurr memenuhi

llprll < rAr,

G.3.2)

dimana y adalah sebuah konstanta positif.

Secara umum Algoritma Daerah Kepercayaan tidak digunakan untuk mencari solusi yang tepat dari submasalah (3.1.3) tetapi dengan suatu solusi yang hampir optimal.

Delinisi 3.3.2

Misalkan Bk = 0, sehingga submasalah (3.1.3) menjadi min/e + prVfk _{dengan llpll < Ar.}

p

57

Pr = -a-g-

ller[l

yang secara sederhana merupakan langkah Steepest Descent dengan panjang langkahnya ditentukan dengan jari-jari Daerah Kepercayaan.

Lemma (3.3.3)

Misalkan pp adalah solusi dari (3.1.3) maka

mr,(o)

- mr(p) > ] ilsnltmin

{tn,ffi,

(3.3.3)

Bukti:

Dengan menggunakan definisi dari pp, untuk setiap a € (0,1], diperoleh mx(o) - mt(p) 2

mr(O)

- (n * etr(-o#*-)

* ;(-"ffino)' n*(-" #ur-))

\

= -etr(-"#u

-)

-:(*"#* r)' ,o(-"#*")

= oL*glg* _ t az f?kele r.e,( llerll 2 llckllz

_ qLkllskll2 _ t az t?a kllskll2 ller.ll 2 llc,kllz

= aArllgrf

l -|aztrtn*

> aakllskll

- | a' nl1ln

*y

) rnzrXo=os,

(olo1;g*

ll -f,arn*llroll)

58

Titik Cauchy (p[) yakni setiap peminimal yang terbentuk oleh langkah Steepest Descent pada submasalah (3.1.3) dapat didefinisikan dengan

mn(pf,)

= min{mr(p)lp

- rpi, llpll < Ar.}

e.3.4)

dimana pf merupakan solusi dari submasalah (3.1.3) dalam bentuk linier, yakni

#nqn

+ sT,P, dengan

llpll < Ar

Solusi dari (3.3.5) adalah

pi:-ffir-oleh karena itu, titik cauchy pada submasalah (3.1.3) dapat dinyatakan dengan

pi= rrpi --xkffit*

(3.3.6) (3.3.5)

iikagT,Bkgr, S 0

Iainnya Q'3'7) dimana

" = {

*m(ffi,r)

59

Lemma 3.3.4

Titik Cauchy p[ memenuhi

mr,(o)

- mn$f,)

> ] tlsoll

*i" {a*,{ff/.

(3.3.s)

Bukti:

Pertimbangkan kasus pertama dari persamaan (3.3.7), yakni gT.Bngn < 0 dan rk = 7, sehingga didapat:

mp(o)

- m*(pl,)

* fi, * (fn + slp"k

+){vD, nu(gtD)

-uT

(-' nffi t.) - :(-'

-#

t-)' B

n

(-, *# *-)

= -eT(-

#*-)

-;(-

#*-)',*(-

#*-)

Angtrg* ttrtgfiakg*

lffi-251r

: A*lls*ll,

_lLTsTBuer

llgrll 2 ller,ll2

>

^kllekll

karena

}!W

= o

> llgrll'nin

{au,.flffJ

Pertimbangkan kasus kedua dari persamaan (3.3.7), yakni

60

, I

llsr,llt

ak \

= -Ek

\-Effi'ns*lls*)

- :(-

ffi. #r-)'

r-

(*

ffi. # r-)

=-etr(

ffi

;(-#ffi)',-(-^-*-',-ffi)

/llsr.ll'zlls,.ll'z\

Ll lle*l['e*\'^ ( llerll2gr\

=

\:Ir--e- )

- 2\- ffi ) "* \ ffi )

llsrlln t (llsrll*elrue*\

=

llg kll4

gT,B

*E* - |ll*,ll* uT,

B ns x

=

*eT,nuenlle*lf

w

1 llskll4

:,TW;

-

1 llgr,lln

= 2ltan111k,*11'

1 llsEll2

=

z llB*ll

6 1

Pertimbangkan kasus ketiga dari persarnaan (3.3.7), yakni

g!Br,gr>

o dan

ffi,

t

(3.3.10)

Pada kasus ini,q, = 1 sehingga didapat

mr(O)

- mrc(p")

= fr, - (fi, + eT,pf,

+f,{vf), n*@"i)

-d (- #*-) -i{-#r-)"

n.(-#'-)

: Aollsull'

*lA?elroen

llgrll 2 llerllz

. ,, ,. 1 A?ogtrBugo

ztrlfgrlt

-Z_ffi

>aknekl|_r&ry

1

itulleull

= * ltro

_L

tl *t,, {n*,

ll*-'!l}

t rrBrlU

Berdasarkan pembuktian dari ketiga kasus di atas, maka lemma terbukti. I

Teorema 3.3.5

(i) Misalkan p;, adalah sebarang vektor sedemikian _{hingga llprll < A1, dan} mr(O) - mn(p*) > c2(m1r(O) - mr(p")) maka pp memenuhi

62

(ii) Secara kfiusus, jika pr, = p[ adala]r solusi eksak dari submasalah (3.1.3),

maka p[ memenuhi

mr,(o) - mn(pr) > cr llgr ll *in [a*, ffi,] dengan

L C < = ' .

Bukti:

(i) Karena llprll < Ak, dari lemma 3.3.4 didapat bahwa

mr(o) - mn(p) > c2(m1,(a)

- mn(pi))

>- lcrllgell min {o*,il#}.

Sehingga teorema 3.3.5(i) terbukti.

(ii) karena p[ adatah solusi eksak dari submasalah (3.1.3) maka

pl e {pr I llpr ll < A1,} sehingga pernyataan (i) berlaku. I

Selanjutny4 untuk membuktikan teorema kekonvergenan global, akan diberikan beberapa lemma.

Lemma 3.3.6

Misalkan asumsi (3.3.1) terpenuhi, maka

l,f(xr + pr) - mk(p)l siullp*llz + c(llprll)llprll (3.3.11)

dimana C(llprll) adalah kecil yang dibatasi ukuran norrn pk. Bukti:

Dengan Teorema Taylor, menurut persamaan _{Q.2.8) dapat ditulis}

f (xr,+pr) = ftxt) + elpt + [ttv/t* r,+ tF*]- v/(xr.)], p*dt

_Js

63

dan

mn{pt)

- f(x*} + gtrpt,

+}vT,novr

maka

lf (xr,+ pr) mk(p)l = l(ft*ol + e|pn+ f tv/(xr * or)

-vf (x;lr po dr) - f Gr) + elpn +|vT,nr,vnl

=

lftoff*r * rpr) - v/(xr)l'podt

-|vT,nnool

= lf fofC*

r, * tpr) - v/(xr)I'pndrl+lullpull'

< ,f,tlv/t*r + rpr) - v/(xr)ll llprlldt

*lullpoll'

= f ,ttrorll llpr,ll

at +|u11p*l1z

= rllpkll2

I! t at +*ullpoll'

= 1 r,llp ull, * 1, llp *ll,

=j*llpoll2

+ c(llprll)llprll.

r

Lemma 3.3.7

Misalkan asumsi (3.3.1) terpenuhi. _{Misalkan bahwa llgrll > e ) 0 dan bahwa} A1, kurang dari suatu batas A. Maka pada iterasi ke-frberlaku Ar+r) Ar.

Bukti:

64

mr(O)

- m*(p*)

r-Irrile*ll*i"

{n-,fl&JIrJ

,lrrrmin {4n,3}

(3.3.r2)

Dari algoritma3.2.l, dengan menggunakan persam&m (3.3.11), (3.3.12), dan (3 .3.2), sehingga diperoleh

tpr,-t'

=1ffi-tl

lf(xJ - ffup+ pr) - (mr(0)

- mk(pr,))l

r l

l*u(p)-f(x*+ pr)l

tffil

* * ilootl'

+ c(lf pk f l) llp,,

ll

-

|c2emin{o*,#}

$r'n7+ c(llprll)r^r

r . ( . E

2c2lmrnt^*,m]

vn*(uyn*

+ zcQlprlD)

c2e

min {o-,#}

batas I, dapat dipilih 6 y*g cukup kecil Karena A1, kurang dari suafu

sedemikian hingga memenuhi

Au< ES e/M, Myan + zc(llprll) s (L - r12)c2e/y,

l p t - 1 l r < L - n z

65

Pandang ruas kanan

L - r t z 2 p n - L

1 + 1 - 4 z 2 P n

2 - n z 2 p r

Pandang ruas kiri

- 1 + q z S p r c - t

- 1 +L*qz<pn

P n 2 4 z

sehingga diperoleh _{pr 2 42.}

Jadi dari algoritna 3.2.1 bahwa Ar+r) Ar.

Teorema 3.3.8

Berdasarkan Asumsi (3.3.1), jika Algoritna 3.2.1 memiliki berhingga banyaknya iterasi yang berhasil yakni p* 2 4u Ak+1= Ap maka Algoritrna 3.2.1 konvergen ke titik stasioner bentuk pertam4 yakni Vf = 0.

Bukti:

Dengan kata lain, teorema di atas dapat dikatakan batrwa jika h 2It artinya Ar+r= Ap maka Yf = 0.Karena Algoritma 3.2.1 hanya memiliki berhingga banyaknya iterasi yang berhasil, maka untuk kyang cukup besar, iterasi tidak berhasil, artinya hlryt maka Ak+r= qtL*,Makq barisan {Ar} dari algoritna konvergen ke nol. Misalkan bahwa ks adalah indeks dari iterasi berhasil yang terakhir.

66

Andaikan _{Vf > 0 sehingga llgu.*tlf > O. Dari Lemma}

Aro*r( A maka berlaku Aro*r*r) Auo*r. Ini kontradiksi

bahwa Ak+r= Ak . Jadi teorema terbukti.

llg inflls;,ll

= 0,

Selanjutny4 perhatian hanya dibatasi pada kasus dimana ada tak berhingga banyaknya iterasi yang berhasil.

Teorema 3.3.9

Misalkan Asumsi 3.3.1 terpenuhi. Jika Algofitna 3.2.1 memiliki tidak berhingga banyaknya iterasi yang berhasil maka barisan {Ar} dari algoritrna 3.2.1 memenuhi

3.3.7 dengan dengan asumsi

(3.3.13)

Bukti:

Dengan kontradiksi, yakni ada e > 0 dan sebuah indeks positif K sedemikian hingga

llekll > e untuksemua k > K.

Dari Algoritma 3.2.1 dan Teorema 3.3.5, mengacu pada iterasi yattg berhasil bahwa pr2Tlumaka

ftx*)- f(x*+ pr)

2 q r P n = _{m*(0) - mr(pn)} sehingga

67

, |n "trllur,

ll min

[o-,

il#J

2|rtrczemin [lr,]] (3.3.14) Sehingg4

f (xr,)-.f(xr*r)

:

l[ft*r) - /('i.r)]

j=o j€s

.)oorrtremin [oo,#] ,

dimana oy adalah banyaknya iterasi yang berhasil sampai iterasi ke -k dengan

lg "-

= *@,

dan S adalah himpunan indeks dari iterasi yang berhasil.

Karcnaf terbatas ke bawah, dari pertidaksamaan di atas haruslah

l*An=

o,

(3'3'15)

Hal ini kontradiksi dengan kesimpulan dari Lemma 3.3.7, yakni Ar*r) Ar. r

Sekarang diberikan hasil yang lebih kuat pada kekonvergenan yang berlaku untuk semua titik limit.

Teorema 3.3.10

Misalkan bahwa Asumsi (3.3.1) terpenuhi. Maka

68

Bukti:

Dengan kontradiksi, bahwa kesimpulan tidak terpenuhi, maka ada sebuah

subbarisan dari iterasi yang berhasil _{{ti} sedemikian} hingga

l f e " l l

> 2 e ) 0 .

(3.3.r7)

untuk sebarang e ) 0 dan untuk setiap i.

Teorema 3.3.9 merfardn bahwa, untuk setiap i, ada, sebuah iterasi pertama yang berhasil l(t) > tt sedemikian hingga llg,A,lll < r. Dilambangkan li a l(t). Maka, ada subbarisan _{Ui] yang lain sedemikian} hingga

l f g r l l

> e u n t u k t i < k ( l s d a n l l g , , l l

< e

( 3 . 3 . 1 8 )

Karena

/(xr) - f(xr*) > q{mn(O) - mr(pr))

2|wremin [an,i]

(3.3.1e)

dari fungsi yang turun secara monoton dan terbatas ke bawah dari barisan {/(x,.)} bahwa

,l*Au= o.

(3.3.20)

Maka

Ans#*V@)-f(xn*)l

(3.3.2r)

yang secara tidak langsung bahwa untuk i ymgcukup besar,

li-L li*L

ll*r,

- *,,11

< 1il., -';*.ll = I o,

69

=#F(*,,) -/(*,,)1.

e.3.22)

Berdasarkan fakta bahwa sisi sebelah kanan konvergen ke nol, maka diperoleh

ll*t, - *,,11

-

o, dimana

i '+ 6,

Sehingga disimpulkan dari kekontinuan tentang gradien bahwa

lle',-Br,ll

-0,

yang mana kontradiksi dengan (3.3.18), karena (3.3.18) mengimplikasikan

bahwa

llgr,

- sr,ll > s.

Jadi terbul;ti. I

Berikut ini akan diberikan tabel perbandingan pengaruh nilai awal dengan hasil akhir dan jumlah iterasi yang diperlukan metode Daerah Keper