ASTRI WULANDARI
G54103018
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2008
ABSTRACT
ASTRI WULANDARI
. The Design of Algorithm to Combined Graph and Simplified Graph in
Knowledge Graph Method. Supervised by SRI NURDIATI and FARIDA HANUM.Text graph is a concept and relation which is represented in a graph type. If two or more text graphs were joined, it will become a combined graph. The purpose of this research is to design an algorithm to join some text graphs into combined graph and to design an algorithm to simplify the combined graph became simpler graph (simplified graph). Steps to combine text graphs are: take some text graphs, analyze those text graphs, make rules from analyze those text graphs, test the rules with some other text graphs until we find basic rule. Steps to make simplify combined graph were almost similar with combine text graphs. The difference is in analyze some text graphs.
From the rule that have been formed, has maded the design of algorithm to combined graph and simplified graph. Among those algorithms can be used to analyze Indonesian document and serve result in a graph type.
From the knowledge graph representation it can be concluded that there are five factors which influence poverty problems and seven factors which influenced by poverty problems. Five factors that influence poverty problems are: lack of skills, low education, low health quality, cultural and structural factor, and capability in technology. Seven factors that influenced by poverty problems are: basic need, technology, infrastructure, institution, human resources, natural resources, and attitude and motivation culture.
ABSTRAK
ASTRI WULANDARI. Perancangan Algoritme Pembentukan Combined Graph dan Simplified Graph pada Metode Knowledge Graph. Dibimbing oleh SRI NURDIATI dan FARIDA HANUM.
Text graph adalah konsep dan relasi yang direpresentasikan dalam bentuk graf.Jika dua atau lebih text graph digabungkan maka akan terbentuk suatu combined graph. Tujuan dari penelitian ini adalah merancang algoritme untuk menggabungkan beberapa text graph menjadi suatu combined graph dan merancang suatu algoritme untuk menyederhanakan combined graph menjadi graf yang lebih sederhana (simplified graph). Langkah-langkah dalam menggabungkan text graph adalah sebagai berikut: mengambil beberapa text graph, menganalisis beberapa text graph tersebut, membuat aturan dari analisis beberapa text graph tersebut, menguji aturan tersebut dengan beberapa text graph lain hingga diperoleh aturan yang baku. Langkah-langkah dalam menyederhanakan combined graph hampir sama dengan penggabungan text graph. Hal yang membedakannya pada saat analisis beberapa text graph.
Dari aturan yang terbentuk, dibuat algoritme pembentukan combined graph dan simplified graph. Kedua algoritme tersebut dapat digunakan untuk menganalisis dokumen berbahasa Indonesia dan menyajikan hasilnya dalam bentuk graf.
Dari representasi knowledge graph dihasilkan gambaran bahwa ada lima faktor yang mempengaruhi masalah kemiskinan dan tujuh faktor yang dipengaruhi masalah kemiskinan. Adapun lima faktor yang mempengaruhi masalah kemiskinan adalah sebagai berikut: keterampilan yang kurang, pendidikan yang rendah, mutu kesehatan yang rendah, faktor kultur dan struktural, dan penguasaan teknologi. Tujuh faktor yang dipengaruhi masalah kemiskinan adalah sebagai berikut: kebutuhan dasar, teknologi, infrastruktur, kelembagaan, SDM, SDA, dan budaya sikap dan motivasi.
PERANCANGAN ALGORITME PEMBENTUKAN COMBINED GRAPH
DAN SIMPLIFIED GRAPH PADA METODE KNOWLEDGE GRAPH
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Oleh:
ASTRI WULANDARI
G54103018
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2008
Judul : Perancangan Algoritme Pembentukan
Combined Graph
dan
Simplified
Graph
pada Metode
Knowledge Graph
Nama : Astri Wulandari
NRP : G54103018
Menyetujui:
Pembimbing I,
Pembimbing II,
Dr. Ir. Sri Nurdiati, M.Sc.
NIP. 131 578 805
Dra. Farida Hanum, M.Si.
NIP. 131 956 709
Mengetahui:
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Dr. Drh. Hasim, DEA.
NIP. 131 578 806
RIWAYAT HIDUP
Penulis dilahirkan di Ciamis pada tanggal 27 Januari 1985 sebagai anak kedua dari tiga bersaudara. Ayah penulis bernama Maman Suhandi dan ibu bernama Kokom Komariah.
Penulis menyelesaikan pendidikan Sekolah Dasar pada tahun 1997 di SD Negeri Ciamis X. Penulis melanjutkan pendidikan ke SLTP Negeri 4 dan lulus pada tahun 2000. Pada tahun 2003 penulis menyelesaikan pendidikan di SMU Negeri 1 Ciamis dan pada tahun yang sama lulus seleksi masuk IPB melalui jalur Undangan Seleksi Masuk IPB (USMI). Penulis diterima sebagai mahasiswa di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.
Selama mengikuti kegiatan perkuliahan, penulis aktif pada kegiatan kemahasiswaan antara lain sebagai staf ahli Gugus Mahasiswa Matematika (GUMATIKA) IPB periode 2004-2005. Penulis juga aktif dalam kegiatan kepanitiaan, antara lain: kepanitiaan dalam rangkaian kegiatan Matematika Ria tahun 2005, LEMM (Let’s Make Money) tahun 2005, Masa Perkenalan Departemen (MPD) Matematika IPB tahun 2006.
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Allah SWT atas segala karuniaNya sehingga penulis dapat menyelesaikan tugas akhir yang berjudul Perancangan Algoritme Pembentukan Combined Graph dan Simplified Graph pada Metode Knowledge Graph. Shalawat dan salam semoga senantiasa tercurah kepada Rasulullah Muhammad SAW beserta keluarga, sahabat dan pengikutnya hingga akhir zaman.
Keterbatasan dan ketidaksempurnaan membuat penulis membutuhkan bantuan, dukungan dan semangat dari orang-orang secara langsung ataupun tidak langsung berkontribusi besar dalam pembuatan tugas akhir ini. Oleh karena itu penulis ingin mengucapkan rasa terima kasih yang sebesar-besarnya kepada :
1. Ibu Dr. Ir. Sri Nurdiati, M.Sc. selaku Pembimbing I, yang dengan sabar telah membimbing dan mengarahkan selama penulisan karya ilmiah ini, Ibu Dra. Farida Hanum, M.Si. selaku Pembimbing II atas bimbingan dan saran yang telah diberikan, dan Bapak Prapto Tri Supriyo, M. Kom. sebagai penguji atas saran dan masukan yang telah diberikan.
2. Bapak, Mamah, Teh Susi, Mas Cahyono, Topan yang selalu memberikan dukungan serta doa restunya selama penulis menempuh pendidikan selama ini. Ponakanku Salsabila dan Ghazy yang memberikan keceriaan, juga keluarga besarku atas dukungan dan doanya.
3. Sahabat-sahabat yang selalu memberikan dukungan dan semangatnya serta nasehat-nasehat yang berharga bagi penulis. Ulfa, Elis, Marlin, Sritie, Dwi, Yuda dan Mayang yang selalu setia mendengar keluh kesah penulis selama ini.
4. Kak Ari, Berri, Mufti, dan Mba Rumsyati yang telah membantu saya dalam mengerjakan penelitian ini.
5. Niken, Lia M, dan Lili atas kesediaannya menjadi pembahas di seminar penulis.
6. Teman-teman kost-an. Andaleb 2 crew: Ame, Linana, Devi, Lina, Nora, Ade, Ratna, Suci, Anri, Yuyun, Noko, Vera, Susi, Mesil, Rima, Sisi, Aci, Atul, Cici, Ratih, Fitri, Wina, Siti, Nisa, Aini dan Apri, atas dukungan, semangat, doa dan kebersamaannya.
7. Keluarga besar Matematika ’40: Aam, Ali, Abay, Vina, Septi, Tiwi, Ifni, Lili, Elis, Ulfa, Berri, Sri, Mayang, Mita, Marlin, Mufti, Manto, Sawa, Mukafi, Yuda, Icha, Azis, Prima, Mika, Uli, Bedu, Jayoe, Komeng, Rusli, Ari, Dwi, Rama, Indah, Anton, Dimas, Walidah, Metha, Achie, Herni, Amie, Gatha, Febrian, Yusuf, Demi, Nisa, dan Putra. Terima kasih atas persabahatan, kebersamaan , dan keceriaan yang telah kita lewati selama masa perkuliahan. Kalian adalah sebaik-baik teman yang selalu menjadikan masa-masa kebersamaan kita penuh warna. Semoga kebersamaan ini akan tetap terjaga.
8. Seluruh dosen Departemen Matematika IPB, atas ilmu yang telah diberikan selama masa perkuliahan. Serta kepada seluruh staf Departemen Matematika, atas bantuan yang telah diberikan.
9. Kakak-kakak mahasiswa matematika angkatan 39, adik-adik mahasiswa matematika angkatan 41 dan 42 yang telah membantu dan memberikan semangat serta doanya.
10.Serta kepada semua pihak yang telah banyak membantu selama proses penyelesaian tugas akhir ini, yang tidak dapat disebutkan satu per satu.
Penulis menyadari bahwa dalam tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan, oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca. Semoga tulisan ini dapat bermanfaat khususnya bagi penulis dan pembaca pada umumnya.
Bogor, April 2008
DAFTAR ISI
Halaman DAFTAR GAMBAR ... ix DAFTAR LAMPIRAN ... ix I PENDAHULUAN 1.1 Latar Belakang ... 1 1.2 Tujuan Penulisan ... 1 1.3 Ruang Lingkup ... 1 II TINJAUAN PUSTAKA 2.1 Graf Berarah (Directed Graph)... 22.2 Knowledge Graph dan Analisis Teks... 3
2.3 Text Graph... 3
2.4 Subgraf Mandiri ... 3
2.5 Problem Area... 4
2.6 Algoritme ... 4
III METODE PENELITIAN... 4
IV HASIL DAN PEMBAHASAN 4.1 Studi Literatur Awal ... 6
4.2 Proses Perancangan Algoritme Penggabungan Text Graph... 9
4.3 Proses Perancangan Algoritme Penyederhanaan Combined Graph... 28
V SIMPULAN DAN SARAN 5.1 Simpulan ... 42
5.2 Saran ... 43
DAFTAR PUSTAKA ... 43
DAFTAR GAMBAR
Halaman
1 Graf dengan enam simpul dan tujuh sisi ... 2
2 Subgraf dari graf di Gambar 1 ... 2
3 Graf berarah dengan enam simpul dan tujuh sisi ... 2
4 Subgraf yang di dalamnya terdapat subgraf mandiri ... 4
5 Subgraf yang di dalamnya tidak terdapat subgraf mandiri... 4
6 Flowchart proses perancangan aturan penggabungan text graph... 5
7 Flowchart proses perancangan aturan penyederhanaan combined graph... 6
8 Hasil analisis Contoh 1 ... 10
9 Combined graph dari Contoh 1... 11
10 Hasil analisis Contoh 2 ... 13
11 Combined graph dari Contoh 2... 13
12 Hasil analisis Contoh 3 ... 15
13 Combined graph dari Contoh 3... 15
14 Hasil analisis Contoh 4 ... 17
15 Combined graph dari Contoh 4... 17
16 Flowchart algoritme penggabungan text graph... 19
17 Output Contoh 5... 21
18 Combined graph dari output Contoh 5 ... 21
19 Output Contoh 6... 24
20 Combined graph dari output Contoh 6 ... 24
21 Output Contoh 7... 26
22 Combined graph dari output Contoh 7 ... 26
23 Output Contoh 8... 28
24 Combined graph dari output Contoh 8 ... 28
25 Hasil analisis Contoh 9... ... 30
26 Simplified graph dari Contoh 9... 30
27 Hasil analisis Contoh 10 ... 31
28 Simplified graph dari Contoh 10... 32
29 Hasil analisis Contoh 11 ... 33
30 Simplified graph dari Contoh 11... 33
31 Hasil analisis Contoh 12 ... 34
32 Simplified graph dari Contoh 12... 34
33 Flowchart algoritme penyederhanaan combined graph... 39
34 Output Contoh 13... 42
35 Simplified graph dari output Contoh 13... 42
DAFTAR LAMPIRAN
Halaman 1 Algoritme pembentukan text graph... 452 Output dari algoritme penggabungan text graph dengan input 36 text graf di 4.1... 48
3 Gambar combined graph dari matriks di Lampiran 2 ... 49
4 Output dari algoritme penyederhanaan combined graph dengan input matriks di Lampiran 2 ... 50
I PENDAHULUAN
1.1 Latar Belakang
Membaca dokumen dalam jumlah besar dapat menimbulkan beberapa masalah. Salah satu masalah tersebut adalah perbedaan interpretasi. Hasil analisis teks pada teori knowledge graph untuk satu persoalan yang sama bisa memberikan hasil yang berbeda. Hal ini disebabkan adanya perbedaan interpretasi yang bersifat subjektif. Masalah lainnya yaitu dibutuhkannya waktu yang lama dalam proses analisis teks.
Metode knowledge graph (KG) muncul pada tahun 1982 di Department of Sociology di Groningen dan di Department of Applied Mathematics di Enschede, Belanda. Penelitian tentang metode ini diteruskan oleh Prof. dr. C. Hoede (Universitas Twente) dengan fokus utamanya adalah aplikasi KG untuk menganalisis teks (Blok 1997).
Menurut Zhang dan Hoede (2002) teori KG merupakan teori yang erat kaitannya dengan masalah natural language yaitu sistem simbol spesial yang digunakan untuk mengekpresikan ide-ide manusia dalam pembentukan informasi menjadi sebuah pengetahuan.
Teori KG merupakan metode baru yang digunakan untuk memahami bahasa manusia yang mengkaji secara luas pada tataran jaringan semantik (arti kata) berupa teks yang bersifat subjektif dan disajikan dalam bentuk graf, sehingga mampu menyederhanakan bahasa yang dipakai sehingga cara pandang dalam menyikapi masalah-masalah tersebut menjadi sama.
Metode KG sudah ada representasinya dalam struktur bahasa Inggris, oleh karena itu perlu dikembangkan representasi KG dalam struktur bahasa Indonesia sehingga dapat digunakan dalam menganalisis dokumen berbahasa Indonesia.
Upaya untuk menerapkan metode KG dalam menganalisis dokumen berbahasa
Indonesia sudah dilakukan oleh beberapa orang, di antaranya: Hulliyah menganalisis teks dengan tema sistem pendidikan nasional (2007), Ikhwati menganalisis teks dengan tema masalah kemiskinan (2007), dan Berri membuat kalimat efektif dan mengonversinya ke dalam bentuk text graph dengan merancang algoritme pembentukan text graph (2008).
Penelitian pada karya ilmiah ini merupakan lanjutan dari penelitian Berri (2008). Dengan kata lain penelitian ini menggabungkan beberapa text graph menjadi
suatu combined graph dan
menyederhanakannya sehingga terbentuk simplified graph. Dokumen yang digunakan dalam karya ilmiah ini yaitu problem area yang terdapat pada skripsi milik Ikhwati (2007). Sebagai upaya untuk menggunakan konsep matematika ke dalam masalah kemiskinan, maka karya ilmiah ini mencoba menerapkan konsep KG.
1.2 Tujuan Penulisan
1. Merancang algoritme untuk
menggabungkan beberapa text graph yang sederhana menjadi suatu combined graph.
2. Merancang algoritme untuk
menyederhanakan combined graph menjadi graf yang lebih sederhana (simplified graph).
1.3 Ruang Lingkup
Ruang lingkup dari penelitian ini adalah menganalisis teks-teks yang berkaitan dengan kemiskinan untuk menentukan konsep dan relasi yang sesuai dengan aturan dari metode KG dalam bentuk graf berarah. Graf-graf tersebut kemudian digabungkan menjadi combined graph, dilanjutkan dengan proses penyederhanaan sehingga terbentuk graf yang sederhana (simplified graph).
II TINJAUAN PUSTAKA
Pada bab ini akan dijelaskan beberapa definisi dan teori yang akan digunakan dalam pembahasan pada bab-bab selanjutnya.
2.1 Graf Berarah (Directed Graph)
Hal penting dalam pengerjaan karya ilmiah ini adalah graf berarah (directed graph, digraf). Sebelum mengetahui definisi graf berarah, perlu diketahui pengertian graf dan subgraf.
Definisi 2.1.1 (Graf)
Graf adalah pasangan terurut (V,E) dengan V adalah himpunan berhingga dan takkosong dari elemen-elemen graf yang disebut simpul (node, vertex) dan E adalah himpunan pasangan takterurut dari simpul-simpul berbeda di V. Setiap {p,q}
∈
E (dengan p,q∈
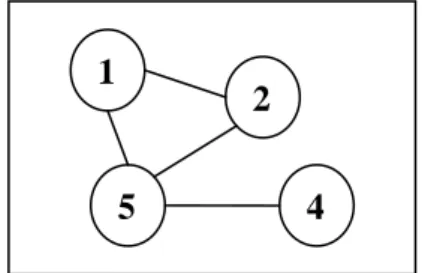
V) disebut sisi (edge) dan dikatakan menghubungkan simpul-simpul p dan q.(Foulds 1992) Sebagai contoh graf dapat direpresentasikan seperti pada Gambar 1 dengan V={1,2,3,4,5,6} dan E={{1,2}, {1,5}, {2,3}, {3,4}, {4,5}, {5,2}, {4,6}}.
Gambar 1 Graf dengan enam simpul dan tujuh sisi.
Definisi 2.1.2 (Subgraf)
Graf G’ disebut subgraf dari G jika semua simpul dan sisi dari G’, juga terletak di G, dan setiap sisi dari G’ mempunyai simpul ujung yang sama dengan di G.
(Martono 1990) G’=(V’,E’) adalah subgraf dari G=(V,E) jika V’ dan E’ di G’ merupakan bagian dari V dan E di G.
(Thulasiraman & Swamy 1992) Sisi pada subgraf bisa merupakan sisi berarah maupun tidak berarah. Sebagai contoh subgraf dari graf di Gambar 1 dapat direpresentasikan
seperti pada Gambar 2 dengan V={1,2,4,5} dan E={{1,2}, {1,5}, {4,5}, {5,2}}.
Gambar 2 Subgraf dari graf di Gambar 1.
Definisi 2.1.3 (Graf Berarah)
Suatu graf berarah (directed graph, digraf) adalah suatu pasangan terurut (V,A) dengan V himpunan takkosong dan berhingga dan A adalah himpunan pasangan terurut dari elemen-elemen berbeda di V. Elemen dari A biasa disebut sisi berarah (arc).
(Foulds 1992) Sisi berarah (arc) merupakan sisi yang menghubungkan antara satu simpul dengan simpul lainnya, dilambangkan dengan tanda panah berarah.
Sebagai contoh graf berarah dapat direpresentasikan seperti pada Gambar 3, dengan V={1,2,3,4,5,6} dan A={(1,2), (1,5), (2,5), (3,2), (4,3), (5,4), (4,6)}.
Pada himpunan arc untuk digraf, urutan pasangan verteks menentukan arah dari arc tersebut.
Gambar 3 Graf berarah dengan enam simpul dan tujuh sisi.
1
2
4
5
1
2
4
5
6
3
1
2
4
5
6
3
2.2 Knowledge Graph dan Analisis Teks Definisi 2.2.1 (Knowledge Graph)
Knowledge graph (KG) adalah suatu metode yang digunakan untuk menganalisis teks dan merepresentasikan teks tersebut ke dalam bentuk graf.
(Zhang & Hoede 2002 dalam Hulliyah 2007) Menurut Kramer (1996) KG adalah suatu instrumen yang merepresentasikan struktur terkonsep yang sudah tertentu. Dengan instrumen ini relasi-relasi antara suatu rangkaian dapat diminimalisir dan terbatas. Tujuannya adalah secara sistematis mengekstrak relasi-relasi dari suatu teks yang menerangkan tentang suatu subjek pada bidang tertentu untuk dituangkan dalam suatu graf (Vries 1989).
Definisi 2.2.2 (Analisis Teks)
Ekstraksi informasi dari teks disebut analisis teks.
(Zhang & Hoede 2002 dalam Ikhwati 2007)
2.3 Text Graph
Sebelum mengetahui definisi text graph, perlu diketahui pengertian konsep dan relasi.
Definisi 2.3.1 (Konsep)
Konsep merupakan komponen terpenting dalam pemikiran manusia. Konsep mampu menjadi prosedur dalam membentuk suatu pengertian dari khusus ke umum atau bahkan sebaliknya. Konsep terdiri dari kata benda dan kata kerja.
(Zhang & Hoede 2002 dalam Hulliyah 2007) Konsep dalam KG bisa dinyatakan sebagai token (simbol, tanda, karakteristik, dan sebagainya). Token adalah konsep yang dipahami oleh seseorang menurut cara pandangnya masing-masing sehingga token bersifat subjektif.
Konsep dalam KG bisa juga dinyatakan sebagai tipe. Tipe adalah konsep yang berupa informasi umum dan bersifat objektif karena merupakan suatu kesepakatan yang dibuat sebelumnya.
Definisi 2.3.2 (Relasi )
Relasi adalah suatu hubungan yang menghubungkan antara konsep yang satu dengan yang lain.
Relasi-relasi yang menghubungkan antara konsep yang satu dengan yang lain
berbeda-beda. Relasi-relasi yang digunakan dalam melakukan analisis teks menurut teori KG di antaranya:
1. Relasi Kausalitas (CAUSALITY= CAU) Dalam relasi ini terdapat hubungan sebab dan akibat yaitu sesuatu memengaruhi sesuatu yang lain.
2. Relasi yang Bertautan (SUBSET= SUB) Bila ada dua token yang menggambarkan
dua rangkaian secara bertautan yaitu sesuatu merupakan bagian dari sesuatu yang lain. Jika A SUB B, maka A⊂B. Relasi ini berkaitan erat dengan konsep kepemilikan, artinya A adalah milik atau bagian dari B. 3. Relasi Kesamaan (ALIKENESS= ALI) Relasi ini digunakan bila antara dua token
terdapat elemen-elemen yang sama. Jika A ALI B, maka A∩B ≠ ∅
.
4. Relasi Attributive (PAR)
Relasi ini digunakan untuk menjelaskan bahwa satu elemen berkaitan dan memiliki sifat elemen lainnya.
(Ikhwati 2007)
Definisi 2.3.3 (Text Graph)
Text graph adalah konsep dan relasi yang direpresentasikan dalam bentuk graf.
(Zhang & Hoede 2002 dalam Hulliyah 2007)
2.4 Subgraf Mandiri
Definisi 2.4 (Subgraf Mandiri)
Subgraf mandiri adalah graf yang menjelaskan kondisi dimana tidak ada konsep yang menjadi bagian dari subgraf ini yang mempunyai hubungan dengan konsep-konsep yang tidak ada dalam subgraf. Hal ini berarti bahwa dalam teks informasi yang digambarkan oleh subgraf tidak bersamaan sama sekali dengan informasi lain dalam teks. Oleh karena itu setiap subgraf mandiri dapat diuji secara terpisah sehingga membuat analisis dari seluruh graf lebih mudah.
(Kramer 1996) Sebagai contoh subgraf mandiri dari graf di Gambar 1 dapat direpresentasikan seperti pada Gambar 4. Subgraf mandiri yang dimaksud yaitu subgraf dengan V={4,6} dan E={{4,6}}.
Gambar 4 Subgraf yang di dalamnya terdapat subgraf mandiri.
Sebagai perbandingan antara subgraf yang mandiri dengan yang tidak mandiri, dapat dilihat pada Gambar 5.
Gambar 5 Subgraf yang di dalamnya tidak terdapat subgraf mandiri.
2.5 Problem Area
Problem area merupakan sebuah teks berupa informasi yang berkaitan dengan masalah kemiskinan.
(Ikhwati 2007)
2.6 Algoritme
Algoritme merupakan jantung kehidupan semua program tanpa kecuali meski untuk aplikasi paling sederhana sekalipun. Algoritme adalah metode presisi yang dapat digunakan komputer untuk menyelesaikan masalah.
Algoritme disusun dari sekumpulan langkah berhingga, masing-masing langkah mungkin memerlukan satu operasi atau lebih.
Algoritme umumnya dirancang untuk menyelesaikan suatu masalah spesifik dan dengan usaha yang paling minimal.
Ciri-ciri algoritme:
• Terdapat nol masukan atau lebih yang diberikan secara eksternal.
• Sedikitnya terdapat satu keluaran yang harus dihasilkan.
• Harus secara sempurna menjalankan apa yang dilakukan.
• Setiap instruksi harus dapat dilakukan secara manual menggunakan pensil dan kertas dalam sejumlah waktu yang berhingga.
• Harus berhenti setelah terbatas operasi.
(Hariyanto 2003)
III METODE PENELITIAN
Pada bab ini akan dibahas mengenai beberapa tahapan yang dilakukan dalam penelitian ini.
Tahapan-tahapan tersebut adalah sebagai berikut:
1. Studi literatur awal
Tahapan ini dilakukan untuk mengumpulkan data atau informasi dari teks tentang masalah kemiskinan, yaitu
mengambil problem area yang
merupakan sebuah teks berupa informasi yang berkaitan dengan masalah kemiskinan dari skripsi milik Ikhwati (2007) yang kemudian diubah menjadi kalimat-kalimat untuk dijadikan text graph dengan menggunakan algoritme pembentukan text graph yang dikerjakan
Berri (2008) (bisa dilihat pada Lampiran 1).
2. Proses perancangan algoritme penggabungan text graph
Tahap ini dimulai dengan pengumpulan text graph-text graph yang dihasilkan dari tahap satu yang akan digunakan sebagai input pada tahap ini. Struktur text graph yang berupa konsep dan relasi tersebut dianalisis kemudian digunakan untuk merancang aturan penggabungan text graph. Berikutnya akan dilakukan pengujian pada aturan tersebut untuk perbaikan aturan. Setelah dilakukan beberapa kali pengujian dengan beberapa text graph yang berbeda secara berulang-ulang, diperoleh aturan yang berlaku untuk sembarang dokumen berbahasa
1
2
4
5
6
1
2
4
5
6
Indonesia. Setelah diperoleh aturan penggabungan text graph maka dibuat algoritme penggabungan text graph dan flowchartnya. Dengan demikian text graph-text graph hasil dari tahap pertama dapat digabungkan menjadi combined graph (suatu graf yang merupakan gabungan dari beberapa text graph) dengan menggunakan algoritme penggabungan text graph yang dihasilkan di tahap ini.
3. Proses perancangan algoritme penyederhanaan combined graph
Pada tahap ini combined graph yang dihasilkan dari tahap kedua digunakan sebagai input. Struktur combined graph yang berupa konsep dan relasi tersebut dipelajari untuk digunakan dalam merancang aturan penyederhanaan combined graph. Berikutnya akan dilakukan pengujian pada aturan tersebut untuk perbaikan aturan. Setelah dilakukan beberapa kali pengujian dengan beberapa combined graph yang berbeda secara berulang-ulang diperoleh aturan yang berlaku untuk sembarang dokumen berbahasa Indonesia. Setelah diperoleh aturan penyederhanaan combined graph maka dibuat algoritme penyederhanaan combined graph dan flowchartnya. Dengan demikian combined graph hasil dari tahap kedua dapat disederhanakan menjadi simplified graph (graf yang lebih sederhana dari combined graph) dengan menggunakan algoritme penyederhanaan combined graph yang dihasilkan di tahap ini. Proses penyederhanaan combined graph di antaranya: pembentukan konsep umum (general concept), pembentukan subgraf mandiri (identifying independent subgraph), dan penghilangan causal chains (reducing causal chains). Sebuah konsep yang secara tidak langsung dipengaruhi oleh konsep lain disebut dengan causal chains.
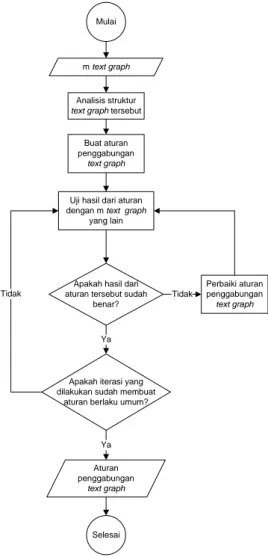
Proses perancangan aturan penggabungan text graph digambarkan dalam flowchart seperti di bawah ini, dengan input m-text graph (beberapa text graph) dan iterasi yang dilakukan lebih dari lima kali.
m text graph
Analisis struktur text graph tersebut
Uji hasil dari aturan dengan m text graph
yang lain
Apakah hasil dari aturan tersebut sudah
benar? Tidak Ya Perbaiki aturan penggabungan text graph
Apakah iterasi yang dilakukan sudah membuat
aturan berlaku umum?
Ya Tidak Aturan penggabungan text graph Buat aturan penggabungan text graph Mulai Selesai
Gambar 6 Flowchart proses perancangan aturan penggabungan text graph.
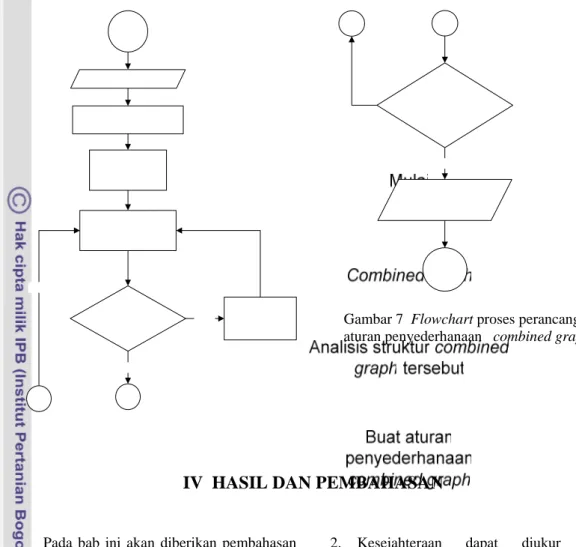
Proses perancangan aturan penyederhanaan combined graph digambarkan dalam flowchart seperti di bawah ini, dengan input suatu combined graph dan iterasi yang dilakukan lebih dari lima kali.
Gambar 7 Flowchart proses perancangan aturan penyederhanaan combined graph.
IV HASIL DAN PEMBAHASAN
Pada bab ini akan diberikan pembahasan dari metode penelitian di bab tiga.
4.1 Studi Literatur Awal
Hal pertama yang dilakukan yaitu mengumpulkan data atau informasi yang dibutuhkan. Data atau informasi tersebut diambil dari skripsi milik Ikhwati (2007) berupa problem area yang merupakan sebuah teks berupa informasi yang berkaitan dengan masalah kemiskinan.
Setelah problem area diperoleh maka problem area tersebut diubah menjadi kalimat-kalimat yang digunakan sebagai input pada algoritme pembentukan text graph. Cara pengubahan problem area menjadi beberapa kalimat dilakukan secara manual sehingga bersifat subjektif asalkan beberapa kalimat tersebut bisa mewakili isi dari problem area. Problem area yang digunakan, yaitu:
1. Kemiskinan dipandang sebagai
ketidakmampuan ekonomi untuk memenuhi kebutuhan dasar baik pangan maupun nonpangan yang bersifat mendasar seperti sandang, perumahan, pendidikan, kesehatan dan sebagainya.
2. Kesejahteraan dapat diukur oleh kekayaan yang dimiliki seseorang, kesehatan, gizi, pendidikan, aset, perumahan, dan hak-hak tertentu dalam masyarakat seperti kebebasan berbicara, sehingga kemiskinan merupakan kurangnya kesempatan atau peluang, ketidakberdayaan, dan kerentanan.
3. Pengukuran kemiskinan yang dapat dipercaya dapat menjadi instrumen yang tangguh bagi pengambil kebijakan dalam memfokuskan perhatian pada kondisi hidup orang miskin, di samping itu data kemiskinan dapat memberikan informasi bagi kebijakan-kebijakan yang ditujukan untuk menurunkan tingkat kemiskinan. 4. Indikator pembangunan infrastruktur
yang sering digunakan dalam pemodelan ekonometrik mencakup akses atau kedekatan terhadap jalan aspal dan listrik, kedekatan terhadap pasar besar, tersedianya sekolah dan klinik di wilayah tersebut, dan jarak ke pusat administrasi atau ibukota.
5. Ada tiga jenis indikator pendidikan yang umumnya digunakan dalam analisis standar hidup rumah tangga yaitu
karakteristik pendidikan anggota rumah tangga, ketersediaan pelayanan pendidikan, dan penggunaan pelayanan tersebut oleh anggota dari rumah tangga miskin dan tidak miskin.
6. Faktor-faktor yang dapat dijadikan sebagai pertimbangan suatu rumah tangga apakah rumah tangga miskin atau tidak miskin yaitu sektor pekerjaan utama, status pekerjaan, jumlah anggota rumah tangga, dan mempunyai sumber penghasilan tetap atau tidak tetap.
7. Beberapa variabel yang mencirikan kemiskinan di pedesaan yang pada umumnya disebabkan karena faktor lemahnya posisi sumber daya manusia, lemahnya sumber daya alam, kurangnya penguasaan teknologi, lemahnya infrastruktur, dan lemahnya aspek kelembagaan, termasuk budaya sikap dan motivasi.
8. Sejumlah variabel dapat dipakai untuk melacak persoalan kemiskinan, di antaranya pendidikan yang rendah, rendahnya mutu kesehatan, penguasaan teknologi dan kurangnya keterampilan, serta faktor kultur dan struktural juga kerap kali dilihat sebagai elemen penting yang menentukan tingkat kemakmuran dan kesejahteraan masyarakat.
9. Berbagai program untuk pengentasan kemiskinan sudah dilansir oleh pemerintah, misalnya program bantuan tunai langsung yang bersifat karikatif sampai program penanggulangan untuk kemiskinan perkotaan yang sifatnya produktif, tetapi tingkat kemiskinan terus mengalami peningkatan.
10. Apa yang kita perlukan untuk mengentaskan kemiskinan di Indonesia adalah menemukan strategi baru yaitu bertolak dari kenyataan sosial tentang kuatnya budaya kemiskinan dan hancurnya modal sosial, dalam konteks ini salah satu fokus strategi ke depan adalah menghidupkan energi sosial masyarakat miskin, mentransformasikan budaya kaku yang turun temurun ke budaya baru sesuai dengan tuntutan perkembangan zaman.
(Ikhwati 2007) Dari problem area No. 1 diperoleh beberapa kalimat di bawah ini:
1. Kemiskinan menyebabkan tidak terpenuhinya kebutuhan dasar.
2. Kemiskinan merupakan ketidakmampuan ekonomi.
3. Pangan termasuk kebutuhan dasar. 4. Nonpangan termasuk kebutuhan
dasar.
Dari problem area No. 2 diperoleh beberapa kalimat di bawah ini:
1. Kemiskinan merupakan ketidakberdayaan.
2. Kemiskinan merupakan kerentanan. Dari problem area No. 3 diperoleh beberapa kalimat di bawah ini:
1. Kebijakan menyebabkan turunnya tingkat kemiskinan.
2. Data kemiskinan dapat berpengaruh pada kebijakan.
Dari problem area No. 4 diperoleh beberapa kalimat di bawah ini:
1. Jalan dan listrik adalah bagian dari infrastruktur.
2. Pasar besar adalah bagian dari infrastruktur.
3. Sekolah adalah bagian dari infrastruktur.
4. Klinik adalah bagian dari
infrastruktur.
5. Pusat administrasi adalah bagian dari infrastruktur.
Dari problem area No. 5 diperoleh beberapa kalimat di bawah ini:
1. Karakteristik pendidikan adalah bagian dari indikator pendidikan. 2. Ketersediaan pelayanan pendidikan
adalah bagian dari indikator pendidikan.
3. Penggunaan pelayanan pendidikan adalah bagian dari indikator pendidikan.
4. Indikator pendidikan dapat
berpengaruh pada analisis standar hidup rumah tangga.
Dari problem area No. 6 diperoleh beberapa kalimat di bawah ini:
1. Sektor pekerjaan utama termasuk dalam faktor pertimbangan rumah tangga miskin atau tidak miskin. 2. Status pekerjaan termasuk dalam
faktor pertimbangan rumah tangga miskin atau tidak miskin.
3. Jumlah anggota rumah tangga termasuk dalam faktor pertimbangan rumah tangga miskin atau tidak miskin.
4. Sumber penghasilan tetap atau tidak tetap termasuk dalam faktor pertimbangan rumah tangga miskin atau tidak miskin.
Dari problem area No. 7 diperoleh beberapa kalimat di bawah ini:
1. Kemiskinan disebabkan oleh
lemahnya sumber daya manusia.
2. Kemiskinan disebabkan oleh
lemahnya sumber daya alam.
3. Kemiskinan disebabkan oleh
kurangnya penguasaan teknologi.
4. Kemiskinan disebabkan oleh
lemahnya infrastruktur.
5. Kemiskinan disebabkan oleh
lemahnya kelembagaan.
6. Kemiskinan disebabkan oleh
lemahnya budaya sikap dan motivasi. Dari problem area No. 8 diperoleh beberapa kalimat di bawah ini:
1. Pendidikan yang rendah adalah salah satu dampak dari kemiskinan. 2. Mutu kesehatan yang rendah adalah
salah satu dampak dari kemiskinan.
3. Penguasaan teknologi bisa
berpengaruh pada kemiskinan.
4. Keterampilan yang kurang adalah salah satu dampak dari kemiskinan. 5. Faktor kultur dan struktural bisa
berpengaruh pada kemiskinan. Dari problem area No. 9 diperoleh beberapa kalimat di bawah ini:
1. Program bantuan tunai langsung dapat mempengaruhi tingkat kemiskinan.
2. Program bantuan tunai langsung adalah bagian dari pengentasan kemiskinan.
Dari problem area No. 10 diperoleh beberapa kalimat di bawah ini:
1. Transformasi budaya kaku ke budaya baru adalah bagian dari pengentasan kemiskinan.
2. Menghidupkan energi sosial
masyarakat miskin adalah bagian dari pengentasan kemiskinan.
Input berupa kalimat di atas akan dijalankan ke dalam algoritme pembentukan text graph yang dikerjakan Berri (2008), dari algoritme tersebut ada beberapa aturan yang diperbaiki. Algoritme pembentukan text graph beserta flowchartnya dapat dilihat pada Lampiran 1. Setelah kalimat-kalimat tersebut diproses melalui algoritme pembentukan text graph, maka akan diperoleh output berupa text graph seperti di bawah ini:
Dari problem area No. 1 dihasilkan beberapa text graph sebagai berikut:
1. Kemiskinan CAU
JJJG
kebutuhan dasar2. KemiskinanALIketidakmampuan ekonomi
3. Pangan SUB
JJG
kebutuhan dasar 4. NonpanganSUBJJG
kebutuhan dasar Dari problem area No. 2 dihasilkan beberapa text graph sebagai berikut:1. KemiskinanALI ketidakberdayaan 2. KemiskinanALI kerentanan
Dari problem area No. 3 dihasilkan beberapa text graph sebagai berikut:
1. KebijakanCAU
JJJG
tingkat kemiskinan 2. Data kemiskinan CAUJJJG
kebijakan Dari problem area No. 4 dihasilkan beberapa text graph sebagai berikut:1. Jalan dan listrik SUB
JJG
infrastruktur 2. Pasar besarSUBJJG
infrastruktur 3. SekolahSUBJJG
infrastruktur 4. KlinikSUBJJG
infrastruktur5. Pusat administrasiSUB
JJG
infrastruktur Dari problem area No. 5 dihasilkan beberapa text graph sebagai berikut:1. Karakteristik pendidikan SUB
JJG
indikator pendidikan2. Ketersediaan pelayanan pendidikan SUB
JJG
indikator pendidikan3. Penggunaan pelayanan pendidikan SUB
JJG
indikator pendidikan4. Indikator pendidikan CAU
JJJG
standar hidup rumah tanggaDari problem area No. 6 dihasilkan beberapa text graph sebagai berikut:
1. Sektor pekerjaan utamaSUB
JJG
faktor pertimbangan rumah tangga miskin atau tidak miskin2. Status pekerjaan SUB
JJG
faktor pertimbangan rumah tangga miskin atau tidak miskin3. Jumlah anggota rumah tangga SUB
JJG
faktor pertimbangan rumah tangga miskin atau tidak miskin4. Sumber penghasilan tetap atau tidak tetap SUB
JJG
faktor pertimbangan rumah tangga miskin atau tidak miskinDari problem area No. 7 dihasilkan beberapa text graph sebagai berikut:
1. Kemiskinan CAU
JJJG
sumber daya manusia2. KemiskinanCAU
JJJG
sumber daya alam 3. Kemiskinan CAUJJJG
teknologi 4. KemiskinanCAUJJJG
infrastruktur 5. KemiskinanCAUJJJG
kelembagaan 6. Kemiskinan CAUJJJG
budaya sikap danmotivasi
Dari problem area No. 8 dihasilkan beberapa text graph sebagai berikut:
1. Pendidikan rendah CAU
JJJG
kemiskinan 2. Mutu kesehatan rendah CAUJJJG
kemiskinan
3. Penguasaan teknologi CAU
JJJG
kemiskinan4. Keterampilan kurang CAU
JJJG
kemiskinan5. Faktor kultur dan struktural CAU
JJJG
kemiskinanDari problem area No. 9 dihasilkan beberapa text graph sebagai berikut:
1. Program bantuan tunai langsung CAU
JJJG
tingkat kemiskinan2. Program bantuan tunai langsung SUB
JJG
pengentasan kemiskinanDari problem area No. 10 dihasilkan beberapa text graph sebagai berikut:
1. Transformasi budaya kaku ke budaya baru SUB
JJG
pengentasan kemiskinan2. Menghidupkan energi sosial
masyarakat miskinSUB
JJG
pengentasan kemiskinan4.2 Proses Perancangan Algoritme Penggabungan Text Graph
Pada proses perancangan algoritme penggabungan text graph, diperlukan beberapa text graph sebagai input, jadi langkah awal yang dilakukan dalam merancang algoritme ini yaitu mengambil contoh beberapa text graph. Kedua, akan dianalisis struktur dari beberapa text graph tersebut apakah ada konsep yang sama antara text graph yang satu dengan text graph lainnya. Output yang akan dihasilkan yaitu combined graph dalam bentuk matriks.
Langkah-langkah dalam menggabungkan beberapa text graph menjadi combined graph akan diilustrasikan dengan contoh-contoh di bawah ini:
Contoh 1.
Beberapa text graph yang diperoleh dari problem area No. 1 adalah sebagai berikut: 1. Kemiskinan CAU
JJJG
kebutuhan dasar2. Kemiskinan ALI ketidakmampuan ekonomi
3. Pangan SUB
JJG
kebutuhan dasar 4. Nonpangan SUBJJG
kebutuhan dasarUntuk penyederhanaan, konsep pada text graph dimisalkan dengan huruf. Misalkan: a: kemiskinan
b: kebutuhan dasar
c: ketidakmampuan ekonomi d: pangan
e: nonpangan
Dengan demikian text graph di atas akan menjadi:
1. aCAU
JJJG
b 2. aALI c 3. dSUBJJG
b 4. eSUBJJG
bBerikutnya, akan dianalisis struktur dari empat text graph tersebut. Konsep pertama pada text graph ke-1, yaitu a, sama dengan konsep pertama pada text graph ke-2, kemudian konsep kedua pada text graph ke-1 yaitu b sama dengan konsep kedua pada text graph ke-3 dan ke-4. Konsep a dan b tersebut akan muncul satu saja di output. Input yang akan digunakan:
Text graph(1): aCAU
JJJG
b Text graph(2): aALI c Text graph(3): dSUBJJG
b Text graph(4): eSUBJJG
bText graph(1) dimasukkan dalam bentuk matriks seperti di bawah, dengan baris dan kolom (a, b): ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 0 0 0 cau
Angka ”0” menyatakan bahwa tidak ada relasi yang menghubungkan antara konsep di baris dengan konsep di kolom.
Text graph(2)
¾ Konsep pertama, yaitu a, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom pada matriks. Karena setelah a ada relasi “ali” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (a, a), sehingga matriks akan berubah menjadi:
⎥ ⎦ ⎤ ⎢ ⎣ ⎡ 0 0 cau ali
¾ Konsep kedua, yaitu c, belum ada pada matriks, maka ada penambahan baris dan kolom c pada matriks, sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 cau ali
Karena sebelum c ada relasi “ali” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (a, a) ke (a, c), sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 cau ali Text graph(3)
¾ Konsep pertama, yaitu d, belum ada pada matriks, maka ada penambahan baris dan kolom d pada matriks. Sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 cau ali
Karena setelah d ada relasi “sub” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (d, a), sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 sub ali cau
¾ Konsep kedua, yaitu b, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom pada matriks. Karena sebelum b ada relasi “sub” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (d, a) ke (d ,b), sehingga matriks akan berubah menjadi:
⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 sub ali cau Text graph(4)
¾ Konsep pertama, yaitu e, belum ada pada matriks, maka ada penambahan baris dan kolom e pada matriks, sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub ali cau
Karena setelah e ada relasi “sub” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (e, a), sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub ali cau
¾ Konsep kedua, yaitu b, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom pada matriks. Karena sebelum b ada relasi “sub” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (e, a) ke (e, b), sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub ali cau
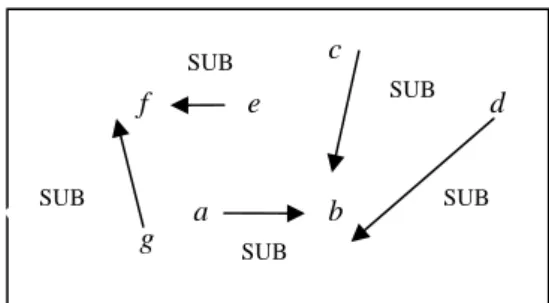
Dengan demikian, hasil analisis beberapa text graph pada Contoh 1 akan membentuk suatu combined graph dalam bentuk suatu matriks seperti pada Gambar 8.
Gambar 8 Hasil analisis Contoh 1. Bentuk combined graph dari Gambar 8 dapat dilihat pada Gambar 9.
⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub ali cau
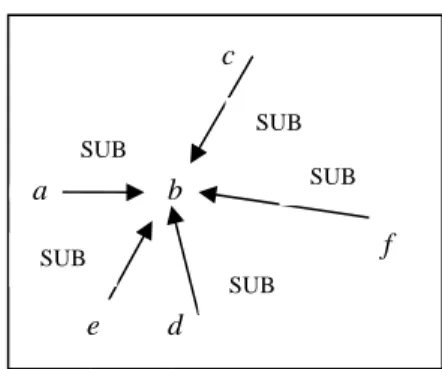
Gambar 9 Combined graph dari Contoh 1. Dari hasil analisis Contoh 1, dapat dibuat aturan penggabungan text graph yaitu:
1. Text graph(1) dimasukkan dalam bentuk matriks sebagai matriks awal dengan baris dan kolom sesuai dengan konsep-konsep yang ada pada text graph tersebut. 2. Jika konsep yang akan diperiksa sudah
ada pada matriks maka konsep tersebut tidak dimasukkan lagi ke dalam matriks. Dengan kata lain tidak ada penambahan baris dan kolom baru pada matriks. 3. Jika konsep yang akan diperiksa belum
ada pada matriks maka konsep tersebut akan dimasukkan ke dalam matriks. Dengan kata lain ada penambahan baris dan kolom baru pada matriks.
4. Jika sebelum konsep yang diperiksa ada relasi maka relasi tersebut dipindahkan ke kolom konsep tersebut.
5. Jika setelah konsep yang diperiksa ada relasi maka relasi tersebut dimasukkan ke baris konsep tersebut tetapi kolomnya pada kolom pertama.
Untuk menguji aturan penggabungan text graph sudah berlaku umum atau tidak, maka diberikan contoh yang lain.
Contoh 2.
Beberapa text graph yang diperoleh dari problem area No. 5 dan 6 adalah sebagai berikut:
1. Karakteristik pendidikan SUB
JJG
indikator pendidikan2. Ketersediaan pelayanan pendidikan SUB
JJG
indikator pendidikan3. Penggunaan pelayanan pendidikan SUB
JJG
indikator pendidikan4. Sektor pekerjaan utamaSUB
JJG
faktor pertimbangan RT miskin atau tidak miskin5. Status pekerjaanSUB
JJG
faktor pertimbangan RT miskin atau tidak miskinUntuk penyederhanaan, konsep pada text graph dimisalkan dengan huruf. Misalkan: a: karakteristik pendidikan
b: indikator pendidikan
c: ketersediaan pelayanan pendidikan d: penggunaan pelayanan pendidikan e: sektor pekerjaan utama
f: faktor pertimbangan RT miskin atau tidak miskin
g: status pekerjaan
Dengan demikian text graph di atas akan menjadi: 1. aSUB
JJG
b 2. cSUBJJG
b 3. dSUBJJG
b 4. eSUBJJG
f 5. gSUBJJG
fBerikutnya, akan dianalisis struktur dari lima text graph tersebut. Konsep kedua pada text graph ke-1, yaitu b, sama dengan konsep kedua pada text graph ke-2 dan ke-3, kemudian konsep kedua pada text graph ke-4 dan text graph ke-5 juga sama, yaitu f. Konsep yang sama tersebut akan muncul satu saja di output. Input yang akan digunakan:
Text graph(1): aSUB
JJG
b Text graph(2): cSUBJJG
b Text graph(3): dSUBJJG
b Text graph(4): eSUBJJG
f Text graph(5): gSUBJJG
fText graph(1) dimasukkan dalam bentuk matriks seperti di bawah, dengan baris dan kolom (a, b): 0 0 0 sub ⎡ ⎤ ⎢ ⎥ ⎣ ⎦
Angka ”0” menyatakan bahwa tidak ada relasi yang menghubungkan antara konsep di baris dengan konsep di kolom.
Text graph(2)
¾ Konsep pertama, yaitu c, belum ada pada matriks, maka ada penambahan baris dan kolom c pada matriks, sehingga matriks akan berubah menjadi: 0 0 0 0 0 0 0 0 sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
Karena setelah c ada relasi “sub” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (c, a),
a b CAU ALI c e SUB d SUB
sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 sub sub
¾ Konsep kedua, yaitu b, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom b pada matriks. Karena sebelum b ada relasi “sub” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (c, a) ke (c, b), sehingga matriks akan berubah menjadi:
⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 sub sub Text graph(3)
¾ Konsep pertama, yaitu d, belum ada pada matriks, maka ada penambahan baris dan kolom d pada matriks, sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub
Karena setelah d ada relasi “sub” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (d, a), sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub
¾ Konsep kedua, yaitu b, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom pada matriks. Karena sebelum b ada relasi “sub” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (d, a) ke (d, b), sehingga matriks akan berubah menjadi:
⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub Text graph(4)
¾ Konsep pertama, yaitu e, belum ada pada matriks, maka ada penambahan baris dan kolom e pada matriks,
sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub
Karena setelah e ada relasi “sub” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (e, a), sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub
¾ Konsep kedua, yaitu f, belum ada pada matriks, maka ada penambahan baris dan kolom f pada matriks, sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub
Karena sebelum f ada relasi “sub” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (e, a) ke (e, f), sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub Text graph(5)
¾ Konsep pertama, yaitu g, belum ada pada matriks, maka ada penambahan baris dan kolom g pada matriks, sehingga matriks akan berubah menjadi:
⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub
Karena setelah g ada relasi “sub” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (g, a), sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub sub
¾ Konsep kedua, yaitu f, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom pada matriks. Karena sebelum f ada relasi “sub” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (g, a) ke (g, f), sehingga matriks akan berubah menjadi:
⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub sub
Dengan demikian, hasil analisis beberapa text graph pada Contoh 2 akan membentuk suatu combined graph dalam bentuk suatu matriks seperti pada Gambar 10.
Gambar 10 Hasil analisis Contoh 2. Bentuk combined graph dari Gambar 10 dapat dilihat pada Gambar 11.
Gambar 11 Combined graph dari Contoh 2. Hasil analisis contoh beberapa text graph yang kedua, tidak ada perbaikan aturan dari aturan yang pertama. Selanjutnya akan ditinjau text graph yang diperoleh dari problem area No. 6 dan 7.
Contoh 3.
1. Jumlah anggota rumah tangga SUB
JJG
faktor
pertimbangan rumah tangga miskin atau tidak miskin2. Sumber penghasilan tetap atau tidak tetap SUB
JJG
faktor pertimbangan rumah tangga miskin atau tidak miskin3. Kemiskinan CAU
JJJG
SDM 4. Kemiskinan CAUJJJG
SDAUntuk penyederhanaan, konsep pada text graph dimisalkan dengan huruf. Misalkan: a: jumlah anggota rumah tangga
b: faktor pertimbangan rumah tangga miskin atau tidak miskin
c: sumber penghasilan tetap atau tidak
d: kemiskinan
e: SDM
f : SDA
Dengan demikian text graph di atas akan menjadi:
1. aSUB
JJG
b 2. cSUBJJG
b 3. dCAUJJJG
e 4. dCAUJJJG
fBerikutnya, akan dianalisis struktur dari empat text graph tersebut. Konsep kedua pada text graph ke-1 yaitu b sama dengan konsep kedua pada text graph ke-2, kemudian konsep pertama pada text graph ke-3 yaitu d sama dengan konsep pertama pada text graph ke-4. Konsep yang sama tersebut akan muncul satu saja di output. Input yang digunakan:
Text graph(1): aSUB
JJG
b Text graph(2): cSUBJJG
b Text graph(3): dCAUJJJG
ea b SUB c d SUB SUB e SUB f g SUB ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub sub
Text graph(4): dCAU
JJJG
fText graph(1) dimasukkan dalam bentuk matriks seperti di bawah, dengan baris dan kolom (a, b): 0 0 0 sub ⎡ ⎤ ⎢ ⎥ ⎣ ⎦
Angka ”0” menyatakan bahwa tidak ada relasi yang menghubungkan antara konsep di baris dengan konsep di kolom.
Text graph(2)
¾ Konsep pertama, yaitu c, belum ada pada matriks, maka ada penambahan baris dan kolom c pada matriks, sehingga matriks akan berubah menjadi: 0 0 0 0 0 0 0 0 sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
Karena setelah c ada relasi “sub” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (c, a), sehingga matriks akan berubah menjadi: 0 0 0 0 0 0 0 sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
¾ Konsep kedua, yaitu b, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom pada matriks. Karena sebelum b ada relasi “sub” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (c, a) ke (c, b), sehingga matriks akan berubah menjadi:
0 0 0 0 0 0 0 sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ Text graph(3)
¾ Konsep pertama, yaitu d, belum ada pada matriks, maka ada penambahan baris dan kolom d pada matriks, sehingga matriks akan berubah menjadi: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
Karena setelah d ada relasi “cau” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (d, a),
sehingga matriks akan berubah menjadi: 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub cau ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
¾ Konsep kedua, yaitu e, belum ada pada matriks, maka ada penambahan baris dan kolom e pada matriks, sehingga matriks akan berubah menjadi: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub cau ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
Karena sebelum e ada relasi “cau” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (d, a) ke (d, e), sehingga matriks akan berubah menjadi: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub cau ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ Text graph(4)
¾ Konsep pertama, yaitu d, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom pada matriks. Karena setelah d ada relasi “cau” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (d, a), sehingga matriks berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 cau cau sub sub
¾ Konsep kedua, yaitu f, belum ada pada matriks, maka ada penambahan baris dan kolom f pada matriks, sehingga matriks akan berubah menjadi:
⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 cau cau sub sub
Karena sebelum f ada relasi “cau” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (d, a) ke (d, f), sehingga matriks akan berubah menjadi: ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 cau cau sub sub
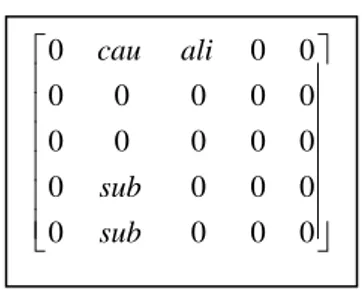
Dengan demikian, hasil analisis beberapa text graph pada Contoh 3 akan membentuk suatu combined graph dalam bentuk suatu matriks seperti pada Gambar 12.
Gambar 12 Hasil analisis Contoh 3. Bentuk combined graph dari Gambar 12 dapat dilihat pada Gambar 13.
Gambar 13 Combined graph dari Contoh 3.
Berdasarkan hasil analisis Contoh 3, tidak ada perbaikan aturan. Selanjutnya akan ditinjau text graph yang diperoleh dari problem area No. 4.
Contoh 4.
1. Jalan dan listrik SUB
JJG
infrastruktur
2. Pasar besar SUBJJG
infrastruktur
3. SekolahSUBJJG
infrastruktur 4. KlinikSUBJJG
infrastruktur5. Pusat administrasiSUB
JJG
infrastruktur Untuk penyederhanaan, konsep pada text graph dimisalkan dengan huruf. Misalkan: a: jalan dan listrikb: infrastruktur c: pasar besar
d: sekolah
e: klinik
f: pusat administrasi
Dengan demikian text graph di atas akan menjadi: 1. aSUB
JJG
b 2. cSUBJJG
b 3. dSUBJJG
b 4. eSUBJJG
b 5. fSUBJJG
bBerikutnya, akan dipelajari struktur dari lima text graph tersebut. Konsep kedua pada text graph ke-1 sampai text graph ke-5 sama yaitu b. Konsep yang sama tersebut akan muncul satu saja di output. Input yang digunakan:
Text graph(1): aSUB
JJG
b Text graph(2): cSUBJJG
b Text graph(3): dSUBJJG
b Text graph(4): eSUBJJG
b Text graph(5): fSUBJJG
bText graph(1) dimasukkan dalam bentuk matriks seperti di bawah, dengan baris dan kolom (a, b): 0 0 0 sub ⎡ ⎤ ⎢ ⎥ ⎣ ⎦
Angka ”0” menyatakan bahwa tidak ada relasi yang menghubungkan antara konsep di baris dengan konsep di kolom.
Text graph(2)
¾ Konsep pertama, yaitu c, belum ada pada matriks, maka ada penambahan baris dan kolom c pada matriks, sehingga matriks akan berubah menjadi: 0 0 0 0 0 0 0 0 sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ a b SUB c SUB d CAU f CAU e ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 cau cau sub sub
Karena setelah c ada relasi “sub” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (c, a), sehingga matriks akan berubah menjadi: 0 0 0 0 0 0 0 sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
¾ Konsep kedua, yaitu b, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom pada matriks. Karena sebelum b ada relasi “sub” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (c, a) ke (c, b), sehingga matriks akan berubah menjadi:
0 0 0 0 0 0 0 sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ Text graph(3)
¾ Konsep pertama, yaitu d, belum ada pada matriks, maka ada penambahan baris dan kolom d pada matriks, sehingga matriks akan berubah menjadi: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
Karena setelah d ada relasi “sub” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (d, a), sehingga matriks akan berubah menjadi: 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
¾ Konsep kedua, yaitu b, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom pada matriks. Karena sebelum d ada relasi “sub” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (d, a) ke (d, b), sehingga matriks akan berubah menjadi:
0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ Text graph(4)
¾ Konsep pertama, yaitu e, belum ada pada matriks, maka ada penambahan baris dan kolom e pada matriks, sehingga matriks berubah menjadi:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
Karena setelah e ada relasi “sub” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (e, a), sehingga matriks berubah menjadi:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
¾ Konsep kedua, yaitu b, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom pada matriks. Karena sebelum b ada relasi “sub” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (e, a) ke (e, b), sehingga matriks akan berubah menjadi:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ Text graph(5)
¾ Konsep pertama, yaitu f, belum ada pada matriks, maka ada penambahan baris dan kolom f pada matriks, sehingga matriks berubah menjadi:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
Karena setelah f, ada relasi “sub” maka relasi tersebut dimasukkan ke posisi (baris, kolom) = (f, a), sehingga matriks berubah menjadi:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
¾ Konsep kedua, yaitu b, sudah ada pada matriks, maka tidak ada penambahan baris dan kolom pada matriks. Karena sebelum b ada relasi “sub” maka relasi tersebut dipindahkan dari posisi (baris, kolom) = (f, a) ke (f, b), sehingga matriks akan berubah menjadi:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sub sub sub sub sub ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
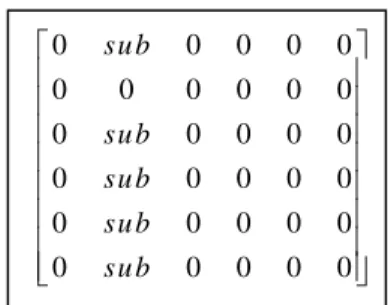
Dengan demikian, hasil analisis beberapa text graph pada Contoh 4 akan membentuk suatu combined graph dalam bentuk suatu matriks seperti pada Gambar 14.
Gambar 14 Hasil analisis Contoh 4. Bentuk combined graph dari Gambar 14 dapat dilihat pada Gambar 15.
Gambar 15 Combined graph dari Contoh 4. Berdasarkan hasil analisis Contoh 4, tidak ada perbaikan aturan.
Lebih lanjut, dilakukan uji hasil analisis text graph di atas dengan text graph-text graph yang lain secara berulang-ulang sehingga diperoleh aturan yang berlaku umum. Berdasarkan analisis yang dilakukan, maka diperoleh aturan penggabungan text graph sebagai berikut:
1. Text graph(1) dimasukkan dalam bentuk matriks sebagai matriks awal dengan baris dan kolom sesuai dengan konsep-konsep yang ada pada text graph tersebut. 2. Jika konsep yang akan diperiksa sudah
ada pada matriks maka konsep tersebut tidak dimasukkan lagi ke dalam matriks. Dengan kata lain tidak ada penambahan baris dan kolom baru pada matriks. 3. Jika konsep yang akan diperiksa belum
ada pada matriks maka konsep tersebut akan dimasukkan ke dalam matriks. Dengan kata lain ada penambahan baris dan kolom baru pada matriks.
4. Jika sebelum konsep yang diperiksa ada relasi maka relasi tersebut dipindahkan ke kolom konsep tersebut.
5. Jika setelah konsep yang diperiksa ada relasi maka relasi tersebut dimasukkan ke baris konsep tersebut tetapi kolomnya pada kolom pertama.
Berdasarkan aturan penggabungan text graph di atas maka dapat dibuat algoritmenya sebagai berikut:
Algoritme Penggabungan Text Graph
Nama : Algoritme yang mengambil input m text graph dan menggabungkannya menjadi sebuah combined graph (dalam bentuk matriks)
Input : m text graph
Output : combined graph dalam bentuk matriks
Keterangan: text graph : konsep dan relasi yang direpresentasikan dalam bentuk graf konsep : bagian dari text graph selain relasi
combined graph : gabungan dari dua atau lebih text graph
a b SUB c SUB d SUB e SUB f SUB 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 su b su b su b su b su b ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦
Begin
Masukkan m text graph {m=banyaknya text graph}
Masukkan text graph(1) dalam bentuk matriks { text graph(1) merupakan matriks awal} j:=2,…,m
{j=indeks untuk menunjukkan text graph ke-}
∀konsep pada text graph(j) i:=1,...,n
{i= indeks untuk menunjukkan konsep ke-} while j ≤
m
while i ≤
n
{n=banyaknya konsep}
if konsep i
pada
text graphj ∃ pada matriks → ∃penambahan baris dan kolom konsep i pada matriks{jika konsep i pada text graph(j) ∃ pada baris dan kolom matriks maka matriks tetap} if sebelum konsep i pada text graph j ∃ relasi →pindahkan relasi pada posisi sementara ke kolom konsep i
{posisi sementara yaitu posisi (baris, kolom)=(konsep i, konsep pertama)} else→ ∃
pemindahan relasi ke kolom
iif setelah konsep i pada text graph j ∃ relasi →masukkan relasi ke posisi sementara
{posisi sementara yaitu posisi (baris, kolom)=(konsep i, konsep pertama)} else → ∃
pemasukan relasi ke posisi sementara
else → ∃ penambahan baris dan kolom konsep i pada matriks
{jika konsep i pada text graph j ∃ pada baris dan kolom matriks maka matriks berubah} if sebelum konsep i pada text graph j ∃ relasi →pindahkan relasi pada posisi sementara ke kolom konsep i
{posisi sementara yaitu posisi (baris, kolom)=(konsep i, konsep pertama)} else→ ∃
pemindahan relasi ke kolom
iif setelah konsep i pada text graph j ∃ relasi →masukkan relasi ke posisi sementara
{posisi sementara yaitu posisi (baris, kolom)=(konsep i, konsep pertama)} else → ∃
pemasukan relasi ke posisi sementara
i++ j++ end while end while end
Secara ringkas langkah-langkah dalam algoritme penggabungan text graph digambarkan dalam bentuk flowchart sebagai berikut:
Text graph(1) dalam bentuk matriks m text graph j:=2 j:=j+1 i:=1 i:=i+1 Apakah konsep i terdapat di matriks?
Tidak ada penambahan baris dan kolom konsep
i di matriks Ya
Ada penambahan baris dan kolom konsep i di
matriks
Tidak
Apakah sebelum konsep i
terdapat relasi?
Pindahkan relasi ke kolom konsep i dan hilangkan relasi bila pada kolom konsep i
sudah ada relasi yang sama. Ya
Apakah setelah konsep i terdapat relasi?
Masukkan relasi ke posisi (baris konsep i,kolom konsep pertama)
Ya
Apakah i=n (banyaknya konsep)?
Apakah j=m (banyaknya text graph)?
Ya Ya Tidak Tidak Tidak Tidak Tidak ada pemindahan
relasi ke kolom konsep i
Tidak ada pemasukan relasi ke posisi (baris konsep i,kolom konsep
pertama)
Mulai
Selesai
Gambar 16 Flowchart algoritme penggabungan text graph.