BAB V SPIRAL TRANSISI

MINGGU 7 & 8

Diskripsi singkat : materi minggu ini berisi tentang lengkung atau busur

transisi yang berupa lengkung priral atau klotoid, dengan sifat-sifatnya dan kegunaannya dalam survey rute.

Manfaat : apabila mahasiswa menguasai pengetahuan ini maka diharapkan akan dapat merencanakan alinemen transportasi lebih baik lagi dalam arti tercapainya kenyamanan dan keamanan berlalulintas.

Relevansi : setelah mengikuti kuliah minggu ini, diharapkan mahasiswa akan lebih memahami persoaalan-persoalan geomatisasi dalam survey rute,.

Learning Outcome : setelah mengikuti kuliah minggu ini mahasiswa dapat menerapkan pengetahuannya dalam merancang rute transportasi yang lebih baik.

BAB V

SPIRAL TRANSISI

Spiral transisi untuk jalan raya dan jalur kereta api adalah sebuah lengkungan yang secara bertahap mengalami perubahan kelengkungan dari lurus menjadi melingkar. Ini sangat penting untuk jalur kereta api yang mempunyai kecepatan tinggi, untuk kenyamanan operasi merubah ketinggian jalur secara halus.

Penggunaan spiral transisi untuk desain jalan raya umumnya mempunyai keuntungan yang sama dengan untuk jalur kereta api , terutama dengan adanya penambahan “faktor keselamatan “ , penamaan dan penyediaan jalur transisional juga mengurangi tendensi penyimpangan dari jalur lalulintas.

Ketika mobil bergerak melebar pada jalan raya kemudian berbelok dengan arah melingkar, kemudi harus di disesuaikan dengan sudut baru, lebih tergantung pada jari-jari kelengkungan. Pergerakan ini tidak bisa dilakukan secara tiba-tiba atau instan tetapi memerlukan interval waktu, juga memerlukan lengkung transisi , panjangnya dengan menggunakan persamaan panjang × waktu.

V.1. Formula Dan Notasi

TS = perubahan titik dari tangen ke spiral SC = perubahan titik dari spiral ke lingkaran CS = perubahan titik dari lingkaran ke spiral ST = perubahan titik dari spiral ke tangent

SS = perubahan titik dari sebuah spiral ke yang lainnya l = garis spiral dari TS ke beberapa titi pada spiral ls = panjang total spiral dari TS ke Sc

θ = sudut pusat dari spiral l

θs = sudut pusat dari garis spiral ls, yang biasa disebut “sudut spiral”

Ө = sudut defleksi spiral pada TS dari inisial tangent ke beberapa titik pada spiral; D = derajat dari lengkungan spiral pada sembarang titik

R = jari-jari

Dc = Derajat perubahan lengkung perpindahan dari lingkaran ke spiral yang menjadi tangent pada SC. Lihat gambar 67.; Rc adalah jari-jarinya

K = Dc/ls = mulai perubahan derajat kelengkungan per feet dari spiral Δ = Total sudut pusat dari kurva lingkaran

Δc = sudut pusat lingkaran sepanjang Lc diperpanjang dari SC ke CS

y = offset tangent dari titik sembarang pada spiral dengan referensi ke TS dan inisial tangent

ys = offset tangent pada SC

x = jarak tangent beberapa titik pada spiral dengan referensi ke TS dan inisial tangent xs = jarak tangent untuk SC

p = offset dari inisial tangent ke PC pada sebagian lingkaran ; p=ys-Rc vers θs k = absis dari perpindahan PC didasarkan ke TS,

k = xs - Rc sin θs.

a = jarak dari PC ke TS pada spiral yang mana digunakan untuk lengkung lingkaran yang exis.

Ts = jarak total tangent = jarak dari PI ke TS , atau dari PI ke ST; Ts = (Rc+p) tan ½ Δ+k

LC = panjang panjang tali busur; LT= tangent panjang ; ST= tangent pendek. Lihat gambar V.1

Ls = 200 θs/Dc ; Dc = 200 θs/ls ; θs = ls Dc / 200; θ = (l/ls)2_{θs ; Ө = θ/3 – Cs = θs/3 (l/ls)}2

- Cs

V.2. Perkembangan Teori Spiral.

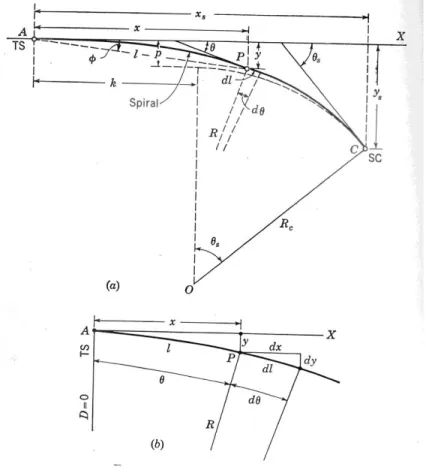
Pada gambar 67, lengkung APCadalah spiral transisi yang berhubungan dengan tangent AX dengan titik C(SC) pada lingkaran. Pada titik A ditangen dimana spiral dimulai (TS) , jarinya terbatas ; pada titik tangensial dengan titik lingkaran , jari-jarinya adalah Rc, dan derajat kelengkungannya Dc,sama dengan lingkaran tersebut; pada beberapa titik tengah spiral (titikP), jari-jarinya adalah R dan derajatnya adalah kurva D, dimana D:Dc = garis AP :garis AC

R= Variabel jari-jari pada beberapa titik P spiral (R=Rc pada SC) l= Panjang garis spiral AP (l=ls pada SC);

θ= sudut pusat dari AP (θ = θs Pada SC)

x dan y = koordinat titik P dengan referensi ke TS dan axis AX ( x dan y menjadi xs

dan ys pada SC)

Karena derajat bervariasi secara langsung terhadap jarak l dari TS, jari-jari adalah berbanding terbalik terhadap jarak: sehingga

R = K/ l (a)

Dimana K adalah konstan .

Pada titik C (SC), akhir dari spiral, persamaan diatas menjadi;

Rc = K/ ls (b)

Eleminasi K dengan membagi(a) dengan (b), diperoleh

R = Rc ls/ l (V.1)

Dari defrensial sektor pada titik P, kita memperoleh dθ=dl/R. Substitusikan nilai R dari pers(80) menjadikan

dθ=l dl/Rc ls

diintegralkan θ=l2/2Rcls (θ dalam radian) (V.2)

karma Rc dan ls adalah konstan, terlihat bahwa θ bervariasi terhadap kuadrat jarakdari TS.

Pada titik C (SC) θ= θs, yang mana sering disebut sudut spiral. karna θ= θs kemudian l=ls ; sehingga persamaan (V.2) menjadi

yang mana θs dalam radian.

Substitusikan 5,729.58/Dc untuk Rc dan θs dalam derajat, maka persamaan (V.3) menjadi

θs=( ls/200) Dc, (V.6) ls=200 θs/ Dc (V.7)

sehingga panjang total lingkaran adalah kedua busur lingkaran pada sudut pusat θs dan jari-jari Rc (dan derajat curva,Dc);

bandingkan persamaan (81) dan (82), kita memperoleh θ:θs = l2:ls2, atau

θ = (l/ls)2θs (V.8)

persamaan (85) rumus yang tepat untuk mencari θ pada beberapa titik sepanjang spiral. Karna l/ls adalah rsio abstrak, θ dan θs dapat dalam radian maupun derajat, yang kemudian cocok untuk hal praktis.

Dari defrensial segitiga pad P (ditunjukkan untuk skala luas) pada gbr.67b, kita memperoleh dy=dl sin θ dan dx= dl cos θ

Perluasan dari fungsi sinus dan cosinus , integral,dan reduksi, kita mendapatkan perkiraan(lihat lampiran C untuk solusi penuh dan rumus yang lebuh akurat):

y =l/100[0.58θ-…], (V.9)

x =l/100[100-0.3046θ2(10)-2 + 0.4296θ4(10)-7 - …] (V.10)

jika l =250 ft, θ=120

, y(table 15) = 0.069595 X 250 = 17.40 ft.

letakkan kembali θ pada pers((86) dengan nilai yang diberikan oleh pers(V.2), kita memperoleh perkiraan

y= l3/6Rcls (V.11)

ditunjukkan bahwa transisi spiral adalah perkiraan dari parabola kubik; sehingga tangen offset mendekati proporsional untuk kubus dengan jarak dari TS .

V. 3. Fungsi Spiral dan Lingkaran.

Pada gambar V.2, dua lengkung spiral memanjang dari TS ke SC dan dari CS ke ST dihubungkan oleh lingkaran ditengah sampai sudut pusat Δc= (Δ- 2θs) derajat. Untuk membuat ruang untuk spiral, lingkaran terbagi dalam dua bagian ke posisi FF’, dimana H”F” = p. memotong PI menjadi dua, disebut “trow,” persamaan p sec ½ Δ. Bagian yang penting, atau fungsi, dari lengkung lingkaran yang dispiralkan adalah (lihat gambar .67a dan 68)

P = HF = ys - Rc vers θs dan k = xs – Rc sin θs dimana xs , ys, Rc, dan θs sudah didefenisikan .

Ini secara nyata digunakan bahwa offset dari H ke spiral sangat dekat ½ (HF) atau ½ p. Juga, garis HF kira-kira membagi dua spiral.

Berdasarkan pada gambar V.2, kita memperoleh Es = total jarak external = (Rc + p ) sec ½ Δ – Rc

= (Rc + p ) exsec ½ Δ+ p, (V.12) Ts = total jarak tangent = (Rc + p ) tan ½ Δ + k (V.13)

Gamabr V.2. Lengkung spiral terkait yang tidak dispiral.

Dimana E dan T adalah external dan jarak tangent untuk tidak membagi dua lengkung lingkaran .

Jika Δ, Dc, dan ls diketahui, Ts dan Es dapat ditentukan dengan mengunakan dua metode: dengan pers (V.12) dan (V.13) atau dengan interpolasi pada table 18 dan 19.

1. Pada aplikasi pers (V.12) dan (V.13), besaran p dan k (untuk ls = 1 stasiun)

diambilsecara langsung dari table 15 dan dikalikan dengan panjang dari spiral, akan ditunjukkan dengan contoh 1.

2. Interpolasi pada tabel 18 dan 19 melebihi rentang 10 baik pada Δ dan θs memberikan hasil yang hampir sama mendekati seratusan feet/ kaki. .

Karna table 18 an 19 didasarkan pada kurva 10 , hal itu akan cocok diaplikasikan untuk kedua busur dan pada definisi tali busur.tik.

Gambar V.3. Bagian dari spiral dan lingkaran oskulasi.

Contoh 1.

Diberikan Δ = 400 20’, Dc = 60, ls = 400 ft.

dibutuhkan perhitungan Ts dan Es , dimana ls = 400 = 200 θs /6, dimana θs = 120

1. Gunakan table 15, nilai dari p dan k adalah p = 1.743 X 4 = 6.97; k = 49,927 X 4 = 199.71 karna Dc = 60, Rc kemungkina didapat pada table 5 atau dari formula Rc = 55729.58/6 = 954.93 kemudian tak ada natural tangent dan external terlihat dapat ditemukan pada table 40 dan 41, kita memperoleh,dari pers(V.12) dan (V.13),

Ts = 961.90 X 0.3672680 + 199.71= 552.99 ft, Es = 961.90 X0.0653102 + 6,97 = 69.8 ft.

2. Masukkan table 18 dengan Δ = 400 20’ dan θs= 120 , kita memperoleh 3,298.87 19.07 ---+ Ts = 3,317.94 (untuk kelengkungan 10 ) Ts (kelengkungan 60) = 3,317.94/6 = 552.99 ft

Dengan cara yang sama dari table 19 , didapat 412.2

6.6 __________+

Es= 418.8 (untuk kelengkungan10); Es(untuk kelengkungan 60) = 418.8/6 = 69.8ft.

Contoh 2

Diberikan Δ = 500 12’, Dc = 8,40, ls= 250 ft. dibutuhkan perhitungan: total jarak tangent Ts

solusi: dari rumus ls = 200 θs/Dc, didapat 250 = 200 θs / 8.4 dimana θs = 10.50 menggunakan table interpolasi dibuat vertikal dan horizontal, dengan pendekatan dibawah.

θs Δ 100 110 50000’ 3,684.28 3,786.79 (61.43 X 12/60 ) 12.29 12.30 (61.49 X 12/60) __________ _________ 50012’ 3,696.57 3,799.09 (102.52 X ½ ) 51.26 __________ 3,747.83 (untuk lengkung 10) 3,747.83 Ts (untuk lengkung 8.40 ) = _______ = 446.17 ft 8.4

catatan : interpolasi ganda dapat menghindari penandaan nilai integral untuk ls dan θs , sedangkan Dc menjadi kecil.

Pada gambar V.3, panjang tangent

(LT, atau U) = AB = AD-BD= xc- yc cot θs ;

Juga tangent pendek (ST, atau V)= BC = yc/ sin θs.dari pada menggunakan furmula ini, panjang dan pendek dari tangent akan lebih mudah didapat dari table 15. Titik B , perpotongan tangent spiral AB dan BC, disebut PIs, adalah koresponden titik didepan tangent.

V.4. Sudut Difleksi.

Pada gambar 67a, ф = 1/3 θ - Cs; atau , ф = 1/3(l/ls)2 θs – Cs (V.14) Dimana Cs (dalam detik) koreksi kecil yang diberikan pada table 20, atau dari rumus Cs (dalam second) = 0.0031 θs3 + 0.0023 θs5 (10)-5 . Pada SC , dimana l/ls = 1,

фc= 1/3 θs- Cs (V.15)

Contoh.

Diketahui Ds = 7015’, ls = 400ft , θs = 150, dan TS pada sta.37+10.2 Ditanyakan; lokasi dari spiral dengan defleksi dari TS dan inisial tangent. Catatan: karena coreksi Cs untuk sudut defleksi akhir hanya 13 detik, ini akan diabaikan

Methode 1. Menggunakan rumus ф= 1/3 θ = 1/3(l/ls)2 θs , ini sangat baik untuk menggekspresikan 1/3 θs dalam menit; jadi 1/3 (150) = 300 menit. Kemudian ф = 1/3(l/ls)2 X 300 menit, diberikan pada table A

Metode 2. Jika spiral dibagi kedalam 10 persamaan dengan masing-masing 40 ft, defleksi titik bagian persamaan diberikan secara langsung pada table 23 untuk θs= 150

. ini adalah prosudur yang simple, tetapi stasiun yang sama belum ditempatkan, yang biasa iinginkan. TABEL A Stasiun l l/Ls 2 s l l Sudut Difleksi 37 + 10,2 TS + 50 38 + 00 + 50 39 + 00 + 50 40 + 00 + 50 41 + 00 + 10,2 ST 0 39,8 89,8 139,8 180,8 239,8 289,8 339,8 389,8 400,0 0 0,100 0,224 0,350 0,474 0,600 0,724 0,850 0,975 1,000 0 0,010 0,050 0,122 0,225 0,360 0,524 0,722 0,951 1,000 0o 0o 03΄ 0o 15΄ 0o 37΄ 1o 07,5΄ 1o 48΄ 2o 37΄ 3o 37΄ 4o 45΄ 5o 00΄

V.5. Prosedur Umum Untuk Memasang Spiral dan Lingkaran.

Dalam artian disini tabel sudah diberikan, ruang kerja pemasangan lengkung spiral lingkaran sangat mudah. Mari kita asumsikan bahwa PI, Δ, dan Dc sudah diketahui. Langkah berikut adalah tipikal (gambar VI.3).

1. Pilih panjang spiral , kemudian sudut spiral mengikuti dari θs = ls Dc/ 200. 2. Tetapkan jarak total tangent Ts dari table 18, atau dari rumus

Ts = (Rc + p ) tan ½ Δ + k (p dan k dari table 15). Degan Ts diketahui, TS (atau ST) diletakkan dengan mengukur dari PI. Juga,dari jarak (Ts-U) dari PI (dimana U=LT, dari table 15), titik B, PIs,ditetapkan. Kemudian SC mungkin ditempatkan didepan (control) sebagai berikut:i:pasang/dirikan teodolit pada B, dibidik dari PI, putar sebesar sudut θs, dan diukur jarak V , dimana V = ST dari table 15.

3. Dengan menyetel teodolit pada TS, nonius pembacaan dibuat 0000’ pada arah tangen, sudut defleksi berubah menjadi kuadrat jarak sepanjang spiral. Defleksi total ke SC adalah 1/3 θs dikurangi koreksi yang biasanya diabaikan.

4. Selanjutnya, dengan menyetel teodolit pada SC, dan diorientasikan kebelakang ..dengan melihat pada TS ataupun PIs, lengkung lingkaran dapat ditentukan dengan cara defleksi seperti biasa.

V.6. Divergensi Sudut dan Jarak .

Jika sebuah garis lurus dan lingkaran mempunyai kelengkungan dan transisi spiral yang konstan, ini adalah sebuah kurva dengan perubahan keluk yang seragam, yang mempunyai perbedaan spiralpada sudut dan offset dari kurva lengkung untuk memberi jarak pada jarak yang sama dari tangent. Ini adalah kegunaan daripada spiral.

Gambar V.4.. Divergensi sudut dan divergensi linier.

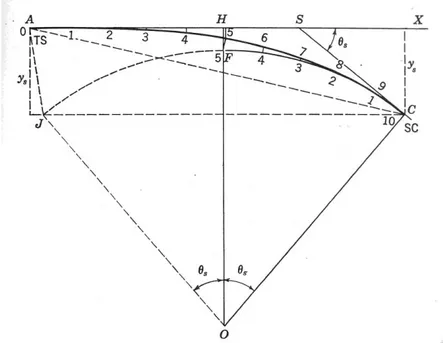
Gambar V.4 menunjukkan penyimpangan spiral dari garis AH dengan offset yang sama dari lingkaran CF. Jika spiral dibagi dalam 10 bagian yang sama, offset dari titik 1,2,3,dst pada lingkaran berhubungan dengan titik 9,8,7,dst pada spiral, sama praktisnya dengan offset tegak lurus dari tangen ke titik spiral 1,2,3,dst.

Dengan posisi di TS ( gb.V.4 ) bacaan nonius 0º00' pada tangen, defleksi ke titik 1,2,3,dst adalah Ө₁, Ө₂, Ө3 ,dst, dimana Ө adalah bervariasi sesuai dengan

kuadrat jarak dari TS. Jika teodolit disetel pada SC dengan bacaan 0º00' pada auxiliary tangen, defleksi ke titik 9,8,7,dst adalah δ₁- Ө₁, δ₂- Ө₂, δ₃- Ө₃,dst, dimana Ө adalah bervariasi sesuai dengan kuadrat jarak dari ST dan sudut-sudut δ nya adalah untuk lingkaran .

Contoh.

Menggunakan data yang sama pada contoh 1 halaman 174, dimana θS = 12º , l_S = 400ft, D_C = 6º, diminta untuk menghitung defleksi dari spiral kedua dari CS (lihat tabel A ).

Gambar. V.5.Memperlihatkan sudut difleksi kemuka dan belakang dari sembarang titik P pada spiral.

Tabel A

Stasiun defleksi

Kurva 6º Tangent spiral pada TS Spiral berdasar tangent pada CS 38 + 00 ( CS ) 0º00' 0º00' 0º00' 38 + 50 1º30' 0º04' 1º26' 39 + 00 3º00' 0º15' 2º45' 39 + 50 4º30' 0º34' 3º56' 40 + 00 6º00' 1º00' 5º00' 40 + 50 7º30' 1º34' 5º56' 41 + 00 9º00' 2º15' 6º45' 41 + 50 10º30' 3º04' 7º26' 42 + 00 ( ST ) 12º00' 4º00' 8º00'

V.7. Defleksi Dari Titik Tengah Spiral.

Fakta bahwa perubahan spiral dari lingkaran pada tingkat yang sama seperti pada tangent, memberikan sebuah metode untuk menentukan lokasi stasiun sebelum atau sesudah titik manapun.

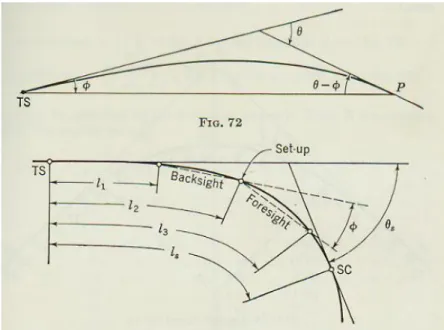
Jika posisi pada titik P ( gb. 71 ), bacaan vernier 0º00' pada auxilliary tangent PS, defleksi ke titik depan P' adalah δ + Ө = defleksi untuk lengkng busur PC' ( = PP' ) dari radius R dan defleksi busur spiral PP', jika titik P di TS. Demikian juga defleksi dari P ke titik di belakang titik P'' adalah δ – Ө.

Contoh. Diberikansudut spiral θS = 16º, DC = 4º, dan TS pada stasiun 31 + 12.4, diasumsikan bahwa stasiun 32 – 36 telah ditentukan melalui defleksi dari TS, tentukan lokasi titik tengah darispiral dengan defleksi dari stasiun 36 + 00.

Penyelesaian . Ls = 200 x 4 16 = 800 ft TS = sta 31 + 12.4 Ls = 8 + 00.0 --- SC = sta 39 + 12.4

DC = derajat kelengkungan spiral padasembarang titik ( sta 36 ), kita dapat DS : DC =

l : l_S dimana l adalah jarak dari TS ke stasiun 36 (= 487.6 ft ). Dari sini diketahui DS = DC x

S l l _{= 4 x} 800 6 . 487 _{= 2.438º = 2º26.28'} Kemudian defleksi dari lengkungan untuk sta. 37, 100 ft ke depan adalah ½ DS = 1º13.14' = 73.14'.

Dengan menggunakan rumus Ө = ( Ls

L

)2x 320' , maka defleksi spiral untuk jarak 100 ft adalah Ө = (

800 100

)2 x 320' = 5 menit.

Dengan posisi di stasiun 36 bacaan vernier 0º00' pada auxilliary tangent, hasil defleksi di berikan pada tabel A.

Tabel A

stasiun Jarak ( ft ) Defleksi δ + Ө

37 100 1º13.14' + 0º05.0' = 1º18.1'

38 200 2º26.28' + 0º20.0' = 2º46.3'

39 300 3º39.42' + 0º45.0' = 4º24.4'

39 + 12.4 ( SC ) 312.4 3º48.50' + 0º48.8' = 4º37.3'

Catatan. Akan dilihat bahwa variasi defleksi lengkungan lingkaran δ berbanding

langsung/lurus dengan jarak dari titik tangent . Sementara variasi sudut defleksi spiral Ө sebanding dengan kuadrat variasi dari jaraknya.

Untuk orientasi alat pada stasiun 36 perlu diketahui total defleksi spiral dari TS ke stasiun 36 yaitu ( 800 6 . 487 )2x 3 16 = 1,981˚=1˚59'

Gambar 72 menunjukan bahwa bacaan sudut dari titik P ke TS adalah δ – Ө =2Ө ( Ө = ₃1θ ). Bacaan sudut pada sta. 36 adalah 3º58', dan jika vernier diubah

menjadi 0º00' dan toropong pada posisi auxilliary tanget.

Metode Alternatif. Rumus umum oleh Kofoid dan didukung oleh Public Road Administration ( pra ) adalah ...Ө = ( l₁ + l₂ + l₃ ) ( l₃ - l₁ ) . ₂

3s s

l (V.9) Dimana θs adalah sudut spiral dan Ө ( pada posisi titik manapun pada spiral ) adalah sudut defleksi dari bacaan belakang maupun depan seperti pada gambar 73.

Apabila posisi alat ukur di Ts, l₁ = l₂ = 0 dan bacaan belakang pada tanget.

Apabila posisi alat ukur di SC, l₂ = l3 = LS dan bacaan depan pada tangent lokal.

.

Apabila alat ukur didirikan pada sembarang titik, sudut defleksi dari bidikan ke tangent lokal dapat dihitung dengan membuat l3 = l2 dan dari bidikan ke depan

dengan membuat l₁ = l₂ .

Hasilnya akurat untuk semua tujuan praktis kecuali koreksi C untuk transisi yang tajam sangat terasa. Tetapi ketika TS dan SC ditentukan langsung dan tidak dengan membawa perubahan stasiun dari TS ke SC, kesalahan tidak terlalu besar dan koreksi C tidak diperlukan.

Kasus Khusus. 10 talibusur spiral . Jika spiral dibagi 10 bagian yang sama,

deflksi ke masing-masing titik diberikan langsung di tabel 20 untuk semua nilai dari sudut spiral θ_S.

V.8. Lengkung Spiral Ganda.

Jika tidak ada busur lengkungan tengah yaitu, jika ΔC = 0 kita mempunyai spiral ganda seperti pada gambar 74 dimana θ_S = ½Δ , Seperti lengkung , secara teori dan perubahannya mengalami perubahan superelevasi yang sangat nyata. Superelevasi dapat dibuat konstan di sekitar tengah kurva sejak deviasi dari spiral dari lingkaran sangat kecil.

Jika Δ = 20 , θS = 10 , lS= 500 ft, yS = 20 ft, dan jarak total = 1000 ft , offset dari tangent ke titik 2 ( 100 ft dari SS ) = ( 1/5 )3 x 29 = 0,23 ft.

Tabel 25 memberikan daftar tangen dan lain-lain pada unit lengkung spiral ganda dan hampir sama dengan tabel 1 untuk lengkungan. Pada contoh yang diberikan , semua stasiun sepanjang lengkungan ditentukan dengan defleksi dari TS untuk spiral pertama dan dari ST untuk spiral kedua.

Contoh. Diberikan Δ = 32˚10' jarak tangent tak terbatas tapi jarak keluar terbatas

kira-kira 48 ft. PI pada sta. 87+12.2. diminta : data-data lengkungan untuk spiral ganda.

Penyelesaian . Tabel 25 memberikan nilai E_S (untuk spiral 100 ft )= 9,683; dimana ratio 48/9,683 = 4,99 = 5.00. Jarak tiap spiral 500 ft. ES= 9,683 x 5 = 48,4 ft; TS = 101,897 x 5 = 509,5 ft.

Sudut spiral = ½Δ = 16˚05' = 965' dengan rumus ( 92 ) dan koreksi CS = 0 didapat, Ө ( menit ) = (

S l

l

)2 x 321,7 untuk spiral pertama ( dari TS ).

Ө ( menit ) = ( S S l l l

)2x 321,7 untuk spiral kedua ( dari ST ).

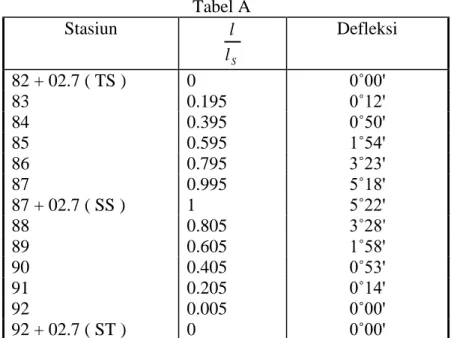
Daat dilihat bahwa semua sudut defleksi pada tabel A mempunyai nilai hampir sama. Tabel A Stasiun S l l Defleksi 82 + 02.7 ( TS ) 0 0˚00' 83 0.195 0˚12' 84 0.395 0˚50' 85 0.595 1˚54' 86 0.795 3˚23' 87 0.995 5˚18' 87 + 02.7 ( SS ) 1 5˚22' 88 0.805 3˚28' 89 0.605 1˚58' 90 0.405 0˚53' 91 0.205 0˚14' 92 0.005 0˚00' 0˚00'

Kesimpulan umum,. Apabila ES terbatas dan TS tidak terbatas, mempunyai nilai hampir sama akan membentuk sebuah spiral dengan sebuah transisi atau perubahan : dan ketika E_S tidak terbatas dan T_S terbatas akan membentuk sebuah kurva lengkung.

V.9. Penggunaan Spiral Pada Lengkung Lingkaran Dimana Bagian Pusat Tidak Dipindah.

Pada gambar 75 diasumsikan bahwa kurva lengkung dari radius R dan derajat kelengkungan D telah ada dan bagian pusat telah beada pada garis lurus tapi akhir dari pembagian dapat dihaluskan sehingga menjadi lingkaran yang berhinpit dengan spiral dan mempunyai tangent yang sama dan berhimpit dengan lengkung yang ada pada titik SC dan CS.

Gambar .V.9. Spiral majemuk dengan busur lingkaran yang tidak dirubah. a = jarak dari PC ke TS. Nilai lS, DC, RC, yS, LT dan ST seperti biasa kecuali bila digunakan pada spiral dengan panjang kira-kira ¾ dari jarak TS ke SC.

y_S, ( gb. 76. ) sama untuk spiral seperti pada lengkung biasa, dimungkinkan untuk mencari panjang dan fungsi lain dari spiral yang akan diperlukan untun proses berikutnya. Appendix D memberikan latar belakang teori untuk tabel 26 yang berisi nilai lS, a, DC, dst yang membentuk spiral. Nilai –nilai tersebut dihitung berdasarkan

basis kelengkungan 1˚ dan berbagai nilai dari sudut spiral θs;nilai-nilai tersebut dapat digunakan pada definisi talibusur dan busur..

Akan dilihat bahwa a kira- kira 1_{3 l}

s; nilai yang pasti diberikan pada tabel 26.

Contoh. Diketahui lengkung lingkaran : Δ = 42˚12.5' , D = 5˚ , dan PC pada stasiun

81 + 11.40. Diasumsikan bahwa PC dan pertengahan lengkungan tetap tidak dipindah. Hitung data lengkung untuk spiral dan pusat lengkungannya.

Penyelesaian : jika jarak spiral lS = 300 ft, lS ( untuk kurva 1˚) = 300 x 5 = 1500 ft dari tabel 26 didapat θ_S = 10˚ 00,2' , a = 500,16/5 = 100,03 ft, D_C = 1,3338x5 = 6,669˚ = 6˚40', yS = 87,11/5 = 17,42 ft , LT = 1,001.61/5 = 200.32, ST = 501,45/5 = 100,29 ft.

Empat nilai terakhir boleh digunakan ataupun tidak pada pemasangan lengkungan. DC diperlukan bila ada titik tengah pada spiral dengan θS = 10˚00.2' ; Δ_S = Δ - 2 θ_S = 22˚12.1', untuk arc pusat lengkung dari jarak 100 x Δ_C/D = 100 x 22.2017/5 = 444.03 ft.

Dengan mengurangkan jarak a ( = 100,03 ft ) dari stasiun PC dicari TS. 81 + 11.43 – ( 1 + 00.03 ) = 80 + 11.40. Dengan posisi pada stasiun 80 + 11.40, TS bacaan mikroskope 0˚00' pada tangent, defleksi untuk posisi stasiun yang lain ditentukan dengan rumus: 3 S ( s l l )2 = ( s l l )2 x 200', dimana θS = 10º = 600'

Catatan Pada contoh selanjutnya Δ = 42˚12,5' dan D = 5˚ E ( tabel 2 ) = 82,4 ft dimungkinkan untuk garis pusat diubah berlawanan PI sehingga E kira-kira 90 ft, kemudian D (harga yang direvisi) =

90 ) 1 (untukkelengkungan 0 E = 4,577º.

Untuk kemudahan perhitungan D = 4,5º ( nilai akhir ), kemudian nilai yang sedikit diperbaiki dari E menjadi

45 ) 1 (untukkelengkungan o E = 5 , 4 925 . 411 = 91,54 ft.

Jika lS = 300 ft, lS ( untuk kelengkungan 1º ) = 4,5 x 300 = 1,350 ft dari tabel 26 kita dapat θ_S = 9º00', a = 5 , 4 ) 1 (untukkurva a = 5 , 4 11 , 450 = 100,02 ft; D_C = 1,3337 x 4,5 = 6,002º, yS = 5 , 4 58 , 70 = 15, 68 dst.

V.10.Spiral Tidak Sama.

Untuk penerapan spiral pada lengkung lingkaran seperti pada gambar V.9 atau V.10, kedua titik akhir spiral mungkin tidak sama panjangnya tanpa diterangkan sebabnya. Busur lengkung tengah telah ada pada posisi dan berhimpit dengan spiral lain.

Misalkan θS dan lS sama dengan sudut spiral dan panjang seperti pada spiral pertama, sementara θS

2

dan lS

2

berhubungan dengan spiral kedua. Dan biarkan tanda-tanda pada lengkung 1 dan 2 sama seperti bagian lain dari spiral pertama dan kedua .

Derajat kelengkungan D sama pada kedua lengkungan, sementara D (D_{C 1} dan D_{C 2} ) akan berbeda.

Misal Δ = 42º12,5' dan D = 5º seperti contoh pada halaman 185 data-data yang telah diketahui diasumsikan dapat digunakan pada kedua spiral. Jika l_S 2 = 400 ft dan l_S 2 (untuk kelengkungan 1º ) = 400 x 5 = 2000 ft. Bedasarkan tabel 26, sehubungan dengan bagian spiral kedua θS2 = 13º20,52', a = 667.02 / 5 = 133.40 ft, D_{C 2} = 1.3342 x 5 = 6,6710º , x_{S 2}= 1,989,2/5 = 397,84 ft, yS2 = 154.64/5 = 30.93 ft

dst.

Catatan : bahwa sudut pusat dari lengkung tengahan lingkaran = Δ_C = Δ – (θS1 + θS2 ) LC = 100 ΔC / D = 100 x 18.8633/5 = 377.27.

Gambar V.10. Menggambarkan sebagian dari gambar V.9.

V.11. Penentuan Lokasi Spiral Dengan Offset.

Offset dari tangen. Diketahui sudut pusat θ pada sembarang titik pada sebuah spiral dengan rumus θ = ( l / l_S )2 _{x θ}

S, hubungan koordinat x dan y dapat ditentukan dengan mengalihkan nilai unit ( dari tabel 15 ) dengan l. Apabila talibusur diukur sepanjang lengkungan, jarak x tidak diperlukan . Offset y boleh diperiksa . Kira-kira dengan mengasumsikan spiralnya sebagai sebuah parabola kubik.

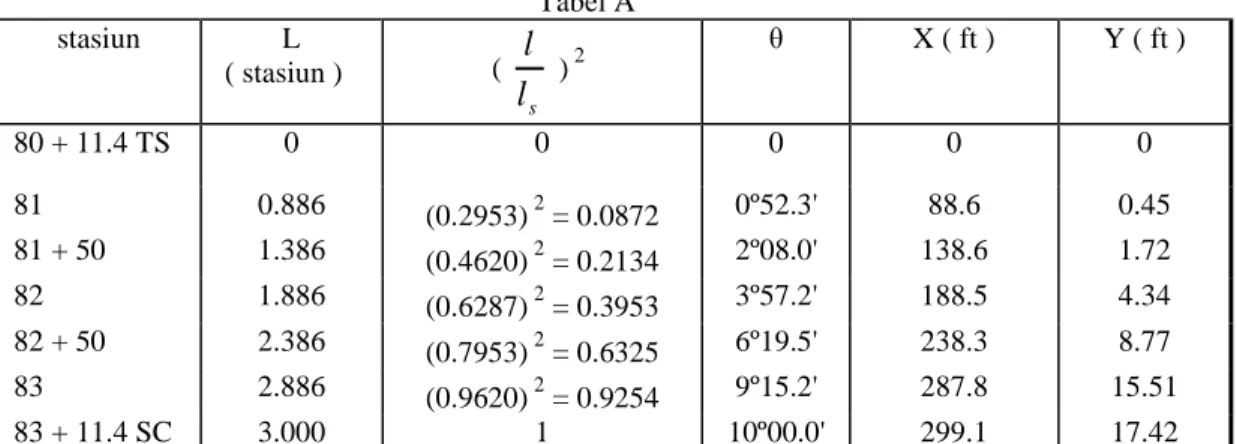
Contoh. Diketahui TS pada sta. 81 + 11.4 , θS ( sudut spiral ) = 10, lS = 300 ft = 3 stasiun . Hitung, koordinat x dan y untuk semua titik pada spiral per 50 ft dari stasiun 81.

Penyelesaian : hitung θ untuk tiap titik , kemudian masukkan tabel 15 untuk nilai unit x dan y yang akan di kalikan dengan l, seperti pada tabel A. sbb:

Tabel A stasiun L ( stasiun ) ( s l l )2 θ X ( ft ) Y ( ft ) 80 + 11.4 TS 0 0 0 0 0 81 0.886 _(0.2953)2 = 0.0872 0º52.3' 88.6 0.45 81 + 50 1.386 _(0.4620)2 = 0.2134 2º08.0' 138.6 1.72 82 1.886 _(0.6287)2 = 0.3953 3º57.2' 188.5 4.34 82 + 50 2.386 _(0.7953)2 = 0.6325 6º19.5' 238.3 8.77 83 2.886 _(0.9620)2 = 0.9254 9º15.2' 287.8 15.51

V.12. Lengkung Spiral Bolak-Balik.

Pada gambar 77 , 2 kurva lengkung HB dan BF’, ditunjukkan dengan garis – garis yang akn pada B (PRC ).

Δ1, Δ2 = sudut luar kurva pertama dan kedua masing- masing , sementara bagian lain adalah D1, D2 ( Derajat kurva ) : T1, T2 ( tangent ) ; L1, L2 ( panjang kurva ) dst. Diminta gambar untuk membuat persekutuan yang mungkin tanpa mengubah gambar yang telah ada...

Metode berikut akan mengenalkan tentang penyelangan tangen. Dengan metode yang sama dimungkinkan digunakan untuk memperpanjang selang tangen pada permulaan yang tidak cukup untuk lintasan superelevasi.

Gambar. V.11. Lengkung spiral bolak-balik.

Dengan asumsi titik tengah M1 yang terletak berlawanan dengan PI dari

lengkungan pertama (lebih tajam) sebagai posisi yang fix, tetapi lengkungan kedua mungkin berubah kerampingannya terhadap pusat tersebut.

Prosedur :

1. Pada titik B (PRC) (gb. 77) dilakukan offset pada sudut kanan ke tangen V1BV2 dengan jarak BN ( = p -

8 1

ys ), dimana p dan y, ditrentukan dari

“sudut spiral” (= 2 1

2. Menelusuri pada tengahan spiral NM1 dengan offset dari lengkungan BM1

atau dengan defleksi ( pertengahan busur yang kanan dari spiral ini dihilangkan ).

3. Memisalkan garis yang melalui N yang sejajar dengan V1V2 memotong

terminal tangen di J.

4. Dengan teodolit di N, menentukan garis pandang pada tangen tengahan spiral NM1 di N. Ini dilakukan dengan memutar sudut JNV’2 ( = F ) dari

garis NJ, dimana F = (₂1

)2 x Fs = 8 1_D

1, setiap sudut berubah sesuai kuadrat jarak dari titik awal spiral.

5. Titik V’2 ( PI baru ) mungkin diletakkan di tanah atau dengan hitungan

berikut : menyelesaikan segitiga NJV’2 untuk JV’2 dan NV’2,, sebagai

bagian yang diketahui adalah sudut di N dan J, dan sisi NJ = BV2 + BN x

tan (90 – D2).

6. Menghitung sudut eksternal baru D’2, bahwa D’2 = D2 – F.

7. Menelusuri sepanjang lengkungan FF’ dengan terminal pada atau dekat dengan F’, titik origin PT.

Ini menunjukkan bahwa panjang selang tangen adalah NF dan bahwa alinemen baru diperbaiki dengan memendekkannya.

Contoh : Diberikan lengkungan bolak-balik dengan data: D1 = 900 , D1 = 30o,

L1 = 300 ft, T1 = 191,0 ft; D2 = 600, D2 = 200, L2 = 300 ft, T2 = 165,4 ft. Dengan asumsi bahwa permulaan selang tangen (seperti gb. V.11).

Penyelesaian : Jika Fs =₂1 D1 = 450, p ( Tabel 15, untuk panjang spiral = 300 ft)

= 6,403 x 3 = 19,21 ft.

Pengoffsetan y dari tangen permulaan pada TS (tidak ditunjukkan pada gb. V.11) bervariasi ketelitiannya pada potongan jarak dari TS, kita mendapatka y (ke titik N) = (₂1 ₎3 _{x y}

s = 8

1_{x 75,147 = 9,39 ft, dimana y}

s ditentukan dari Tabel 15, Tabel 15,

untukFs = 450 dan ls 300 ft. Kemudian BN = 19,21 -9,39 = 9,82 ft.

Sudut JNV’2 = F = 4 1_F

NJ = BV2 + 9,82 x tan (90 – D2) = T2 + 9,82 x tan 300 = 165,40 +5,67 = 171,07 ft. JV’2 = ' 48045 sin 07 . 171 x sin 11015’ = 44,39 ft, NV’2 = ' 4845 07 , 171 x sin 1200 = 197,05 ft, V2V’2 = 44,39 + 9,82 x sec300 = 55,73 ft.

Dengan asumsi bahwa PT dari lengkungan kedua tidak mengalami perubahan , V2F’ =T2 – V2V’2 = 165,40 -55,73 ft = T’2 = panjang tangen hasil perbaikan.

NF = panjang selang tangen = NV’2 – FV’2 = 197,95 – T’2 = 197,05 –109,67 =

87,38 ft.

Panjang perbaikan lengkungan FF’ = 100 x

0 2 T ' T = 205,95 ft, dimana T0 =

panjang tangen (Tabel 1) untuk lengkungan dengan panjang 100 ft dan ’2 = 48045’.

Derajat kelengkungan FF’ = 100 x 95 , 205 75 , 48 = 23,6710.

Ini berarti jarak antara tangen NF dan busur FF’ adalah 6,67 ft lebih pendek dari busur BF’; juga lintasan superelevasi 87,38 ft bertambah ketika tanpa existed pada layout awal.

V.13. Spiral Sejajar (Paralel).

Pada gb. VI.10, R = variabel garis tengah spiral pada jarak l dari TS; R0 =

variabel radius dari bagian luar spiral paralel; Ri = variabel radius bagian dalam spiral

paralel. Pada SC, R = Rc, Ro = Rc + ωωωωw , dan Ri = Rc – ω, dimana Untuk beberapa differensial busur dari panjang dl berdampingan dengan sudut pusat dθ (gb. 78b), hubungan konsentis luar dan dalam dari busurmasing-masing adalah dlo = ( R + ω )dθ dan dli = ( R – ω) dθ sedangkan dl = R dθ

Perhatikan bahwa θ = (l/ls)2Х θs, yang daripadanya dθ= 2l / ls2 Х θs, kita mempunyai dl0 = R dθ+ ωdθ = dl + ₂

ls l 2

dimana R dθ= dl.

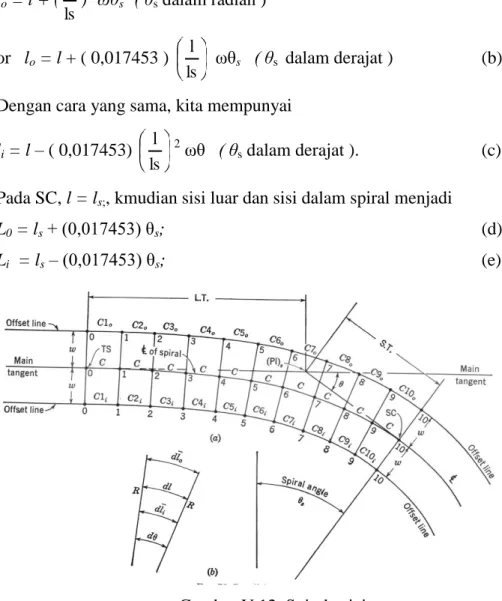
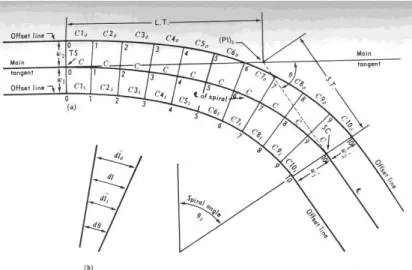
Dengan menyatukan, kita mendapatkan lo = l + ( ls l )2 ωθs ( θs dalam radian ) or lo = l + ( 0,017453 ) ls l ωθs ( θs dalam derajat ) (b)

Dengan cara yang sama, kita mempunyai li = l – ( 0,017453)

ls l ₂

ωθ ( θs dalam derajat ). (c)

Pada SC, l = ls;, kmudian sisi luar dan sisi dalam spiral menjadi

L0 = ls + (0,017453) θs; (d)

Li = ls – (0,017453) θs; (e)

Gambar V.12. Spiral sejajar.

Pematokan dengan Sudut Defleksi. Diketahui panjang lengkungan dan sudut spiral Ө, yang masih perlu disamakan terhadap garis pusat spiral, bagian luar dan bagian dalam spiral paralel diletakkan di suatu tempat dengan sudut defleksi untuk mendapatkan beberapa titik yang diinginkan sepanjang lengkungan .

Bagain luar dan bagian dalam spiral paralel harus berlawanan secara radial terhadap garis tengah spiral, keduanya terletak pada TS dan pada SC, karakteristik

spiral dari lenkungan-lengkungan ini berkurang kerampingannya ( tidak terlalu besar ) gabungan pada Sc.

Pematokan dengan Offset. Dua prosedur yang mungkin digunakan untuk memancang bagian luar dan dalam lengkungan-lengkungan paralel: (1) membagi garis tengah lengkungan dengan bagian yang sama (2) titik-titik pada lengkungan paralel diletakkan berlawanan dengan setasiun penuh pada garis tengah lengkungan.

1. Misalkan garis tengah lengkungan dibagi dengan n bagian yang sama. Denagn membagi garis tengah lengkungan dalam bagian yang sama, persamaan (b) menunjukkan bahwa panjang dari bagian pertama (disebut clo) adalah :

clo = n ls + (0,017453) ₂ n 1 ωθs.

Pada bagian-bagian selanjutnya , dalam suatu rangkaian, bertambah dengan konstanta penambahan yang meliputi 2/n2, diferensial kedua 1/n2, 4/n2, 9/n2, 16/n2,dst. Oleh karena itu, biasanya, konstanta penambahan (disebut CI) adalah

CI = (0,034906) ₂

n (V.17)

Persamaan (94) memberikan koreksi sebagai penambahan ke (atau subtrasi dari) tiap potongan yang berurutan.

Perlu dicatat bahwa sisi luar potongan pertama (disebut clo) selalu sama

dengan ls/n ditambah dari satu-setengah dari penambahan CI.

Pengoffsetan patok dipasaang dengan meletakkan secara berturutan potongan yang terkoreksi pada jarak radial ω yang diinginkan dari titik-titik garis tengah /sumbu lengkungan. Pilihan metode pendirian garis bagian dalam dari patok-patok adalah seperti berikut: setelah pemasangan patok-patok garis bagian luar dengan metode di atas, pengukuran kedua dari jarak offset sisi luar patk, melalui pengukuran jarak secara langsung dengan pita baja yang berakhir pada titik tali busur di garis tengah .

Contoh 1. Diberikan ω= 15 ft, ls = 300 ft, Dc = 60, dari data θs = 90. Diminta

:secara berturutan bagian luar dan bagian dalam talibusur apabila garis sumbu lengkungan dibagi kedalam enam bagian yang sama sebesar setiap 50 ft.

Penyelesaian. Dengan n = 6, Persamaan. (94) memberikan CI = (0,034906) x 15 x_{3 6}9

= 0,131 ft. Potongan-potongan tali busur : cl0 = 50,065; cli = 49,935 c20 = 50,196; c2i = 49,804 c3o = 50,327; c3i = 49,673 c40 = 50,458; c4i = 49,542 c50 = 50,589; c5i = 49,411 c60 = 50,720; c6i = 49,280 302,355 297,645

2. Titik-titik pada spiral sejajar yang berlawanan dengan stasiun tetap

Contoh 2.

Diberikan ω = 15 ft, ls = 300 ft, Dc = 60, Өs = 9 0 ( sama dengan data pada

contoh ). Juga diasumsikan PC pada sta. 15 + 60. Diminta: secara berturutan potongan luar dan potongan dalam.talibusur.

Penyelesaian : Dengan persm. (b), l0 = l + (0,017453)(l/ls)2 x 15 x 9 = l +

(2,35616)(l/ls)2 = l + lengkungan tambahan Pentabulasian hasil-hasil berikut akan

Stasiun l ls l 2 ls l Penamba han lengk. lo c0 ci 51 + 60 0 0 0 0 0 > 40,042 39,958 52 40 0,1333 0,0178 0,042 40,042 >50,170 49,830 52 + 50 90 0,3 0,09 0,212 90,212 > 50,301 49,699 53 140 0,4667 0,2178 0,513 140,513 > 50,432 49,568 53 +50 190 0,6333 0,4011 0,945 190,945 > 50,563 49,437 54 240 0,8 0,64 1,508 241,508 > 60,848 59,152 54 +50 300 1 1 2,356 302,356

V.14. Spiral Tidak Sejajar Baik Bagian Luar dan Bagian Dalam Dimana Jarak Radial Sebagai Variabel.

Pada gb.VI.13, R = variabel radius garis tengah spiral pada beberapa titik yang berjarak l dari TS; Ro = variabel radius dari bagianluarlengkungan; RI = variabel radius

dari bagian dalam lengkungan, bagian luardan dalm lengkungan nonparalel ini bukan langsung spiral sebenarnya, tetapi mereka sebagai representasi yang baik dari garis referensi); Rc = Radius lengkungan lingkaran pada SC, Ro = Rc + ω’2, RI = Rc – ω’1.

Δω sama dengan konstan atau variabel pertambahan radial. Jika garis tengah lengkungan dibagi dalam n bagian yang sama, Δω = ( ω’1 – ω1 )/ n pada sisi dalam.

Ketika garis tengah lengkungan diawali dan diakhiri dengan subpotongan, prosedur modifikasi perampingan akan ditunjukkan selanjutnya.

dlo = (lihat gb. 79b) = R dθ + (ω2 + Δω)dθ

= R dθ + ω2 dθ + Δω dθ. (a)

Subtitusi pada persm. (a) R dθ= dl, dθ = (2l / ls2) θs,

Δω = (l / ls ) (ω’2 – ω2), kita mendapat dlo = dl + ω2 ₂ 2 ls l θs + ₃ 2 2 lsls ( ω’2 – ω2)θs, (b)

Dimana θs = sudut spiral dalam radial (dikalikan dengan 0,017453 jika dalanm

derajat).

Integrasi dalam persm. (b), kita mendapatkan

Lo = l + ω2 ls l 2 (θs) + 3 2 3 ls l ( ω’2 – ω1)θs. (VI.18) Demikianjuga lI = l – ω1 2 ls l (θs) + 3 3 2 ls l (ω’1 – ω1) (θs). (VI.19)

Dengan menggunakan notasi yang sama seperti subbab (93) dimana C10, C20,

C30, dst., sama dengan potongan luar secara berturutan, juga C10, C20, C30, dst., yang

sesuai dengan talibusur atau busur, sebagaimana ditunjukkan pada gb. 79.

Gambar VI.13. Spiral luar dan dalam tidak s4jajar dimana jarak radialnya sebagai variabel.

L10, l20, l30, dst., sama dengan jarak busur sepanjang lengkungan luar yang

sama dengan jarak busur l1, l2, l3, dst., sepanjang sumbu lengkungan. C10 = l10, C20 =

C10 = l10 = l1 + ω2( ls l )2 (θs) + 3 2 _(ω’ 2 – ω2) ls l₁ (θs), (c) C20 = l2 – l1 + ω2 2 1 2 2 ls l ls l (θs) + ₃2( ω’2 – ω2) 3 1 3 2 s s l l l l (θs), (d) C30 = l3 – l2 + ω2 2 2 2 3 s s l l l l (θs) + 3 2_(ω’ 2 – ω2) 3 2 3 3 s s l l l l (θs), dst .(e) Demikian juga C1I = l1I = l1 – ω1 2 1 s l l (θs) - 3 2_{( ω’} 1 – ω1) 3 1 s l l (θs), (f) C2I = (l2 – l1) - ω1 2 2 2 2 s s l l l l (θs) - 3 2_{( ω’} 1 – ω1) 3 1 3 2 s s l l l l (θs),dst (g)

Jika garis tengah lengkungan dibagi dalam bagian yang sama, l1 = l2 – l1 = l3 –

l2 = ls /n, dst. Jika ini di mulai dengan sub potongan, maka l1 kurang dari ls/n. Dengan

tiap bagian garis tengah = ls/n, hal ini berati C10 + C20 + C30 + . . . Cn0 menjadi

Cn = ls + ω2 x1,0 x θs + 3 2 _(ω’ 2 – ω2) x θs; (h) juga C1i + C2i + C3i + . . . Cni = ls – ω1 x 1,0 x θs - 2 3 _(ω’ 1 – ω1) x θs. (i)

Persamaan (h) dan (i) digunakan sebagai cheking.

Apabila garis rtengah lengkungan diaωali dan diakhiri dengan sub potongan, cheking yang mudah dapat ditemukan dengan mudah.

Jika jarak radial ke lengkungan bagian luar di samakan, kemudian (ω’2 – ω2) =

Contoh. Diberikan ls = 300 ft, Dc = 60 ( dari θs = sudut spiral = lsDc/200 = 90),

n = 6, ω2 = 20 ft, ω’2 = ft, ω1 = 21 ft, dan ω’1 = 27 ft. Diminta; secara berturutan

potongan luar dan dalam atau busur apabila garis tengah lengkungan dibagi dalam 6 bagian yang sama sebesar 50 ft.

Penyelesaian. ω untuk lengkungan bagian luar adalah 6

20 23

= 0,5 ft; ω

untuk lengkungan bagian dalam adalah 6 21 27 = 1,0 ft. Dengan Persm. (b), (c), (d), dst., C10 = 50,088721, C20 = 50,291980, C30 = 50,463967, C40 = 50,874119, C60 = 51,092228. Dengan total 33,45575.

Dengan persamaan. (i), total 300 + 20 x θs + 3

2 _{x 3,0 x θ}

s = 300 + 3,1416 +

0,3142 = 303,4558 (cheking).

Dengan Persm. (e), (f), (g), dst.,C1i = 49,90561, C2i = 49,704748, C3i =

49,486583, C4i = 49,250962, C5i = 48,997886, C6i = 48,72737. Total adalah

296,073007.

Dengan Persm. (i), Totalnya adalah 300 – 21 x θs -₃2 x 6 x θs = 300 – 3,2987 –

0,683 = 296,0730 (cheking).

Soal-soal latihan.

1. Diketahui Δ = 40o 12’, Dc = 40 00’ (definisi busur), dan ls = 400ft . Hitung Ts dengan Tabel 18 dan cek dengan menggunakan persamaan (90). Jwb: θs = 8o 00’;Ts = 725,76 ft.

2. Soal sama dengan No.1 di atas, Dc = 5o. Jwb : θs = 10o 00’; Ts = 621,28 ft. 3. Diketahui data seperti soal No. 1, hitung defleksi dari TS (asumsikan pada

stasiun 88 + 19,5) ke stasiun 89 + 00. Jwb : (untuk definisi yang lain dari D) 0o06,5’.

4. Diketahui sudut spiral θs = 8o 00’. Hitung defleksi dari TS ke titik 6. 8, dan

10 (SC) dari sepuluh talibusur spiral. Prosedur, gunakan tabel 23, dan cek dengan persamaan 91. Jwb : 0o57,6’; 1o 42,4’ ; 2o 40,0’.

5. Teodolit disetel pada titik 7 dari sepuluh talibusut spiral, bacaan pada auxilary tangen dibuat 00o 00’, dan sudut spiralnya θs = 6o 00’. Gunakan

6. PC dari lengkung lingkaran dengan D = 6o 00’ pada stasiun 85 + 32,48, Δ = 36o 36’, dan L = 610 ft. Titik tengah ke tiga dari lengkung ini sudah fixed/tetap tetapi titik akhir ketiga (setiap sudut pusat berkisar 12o 00’) mungkin dipertajam agar dapat dispiralkan. Apabila sudut spiral θs = 12o

7. 00’, Tentukan lokasi TS dan SC. Hint : gunakan Tabel 26 untuk θs= 12o 00,39’. Jwb : Sta 84+32,44; Sta. 87+ 32,44.

Tugas :

Mahasiswa diberikan tugas untuk menyelesaikan 3 buah soal dari 7 soal diatas.dan mendiskusikan hasilnya didepan kelas.

Latihan :

Diskusi kelompok membahas materi busur peralihan spiral, baik yang tunggal, majemuk dan bolak-balik.

Rangkuman :

Referensi

1. Hickerson, T.F., 1964, Route Location and Design, Fifth Edition, Mc. Graw-Hill Book Company, New York.

2. Irvine,., 1995, Penyigian untuk Konstruksi, Edisi kedua, Penerbit ITB Bandung.

3. Kavanagh,B.F.,1997. Surveying with Construction Application, Prentice Hall Inc, New Jersey.

4. Meyer, C.F., 1970, Route Surveying, Mc Graw-Hill Book Company, New York.