Fakultas Ilmu Komputer
5525
Pemilihan Aturan
Fuzzy Inference System
Mamdani Menggunakan
Algoritme
Particle Swarm Optimization
Dalam Sistem Penyiraman Otomatis
Pada Tanaman Tomat
Indah Larasati1, Budi Darma Setiawan2, Mahendra Data3
Program Studi Teknik Informatika, Fakultas Ilmu Komputer, Universitas Brawijaya Email: 1[email protected], 2[email protected], 3[email protected]
Abstrak
Laboratorium Tanah Benih Balai Pengkajian Teknologi Pertanian (BPTP) Jawa Timur merupakan salah satu tempat kerja yang bertugas melakukan pengkajian tanah untuk pembibitan tanaman. Salah satu pengujian tanah pada Laboratorium Tanah BPTP Jatim adalah pengujian parameter kelembapan tanah. Saat ini di tempat tersebut sedang dikembangkan alat siram otomatis berdasarkan sensor kelembapan tanah untuk memprediksi kebutuhan volume air yang berfungsi untuk menjaga kelembapan media penumbuhan benih. Penelitian ini akan menghitung banyaknya volume air tanaman dengan dua variabel masukan yaitu kelembapan awal dan lama waktu siram menggunakan metode Fuzzy Inference System Mamdani. Kedua variabel tersebut dapat menyebabkan aturan fuzzy sering terulang atau aturan yang sama digunakan lebih dari satu. Untuk menghindari hal tersebut, maka diperlukan pemilihan aturan
fuzzy dengan menggunakan algoritme Particle Swarm Optimization. Pengujian sebanyak 10 kali percobaan dengan menerapkan jumlah partikel sebanyak 250, nilai bobot inersia (w) adalah 0,7, nilai kombinasi C1 dan C2 adalah 1,4 dan 1,3, dan iterasi maksimalnya adalah 2500, maka diperoleh nilai
fitness tertinggi pada percobaan ketujuh yaitu sebesar 1,39949 dengan nilai Root Mean Square Error
(RMSE) sebesar 1,50319. Hasil dari nilai fitness tertinggi tersebut mampu memilih aturan yang awalnya 27 aturan menjadi 8 aturan.
Kata kunci: pengujian tanah, fuzzy inference system, mamdani, algoritme Particle Swarm Optimization, pemilihan aturan fuzzy.
Abstract
Laboratorium Tanah Benih Balai Pengkajian Teknologi Pertanian (BPTP) East Java is one of the institutes to do some research on plant nursery. One of soil testings which have been done in Laboratorium Tanah BPTP East Java is the parameter testing soil humadity. The research laboratory, right now, is developing an automatic watering based on soil humadity sensory to predict the amount of water needed to keep the humadity of the growing seed media. This research will figure out how much water plant volume with two input variables which are the initial humadity and flushing duration using
Fuzzy Inference System Mamdani method. The two variables can cause often repeated rule based fuzzy
or the same rule used more than once. Thus, to prevent these things to be happened, it needs fuzzy rule base fuzzy choice by using Particle Swarm Optimization algorithm. The testing was done in ten times trials by applying the amount of particles which is 250, value of inertia quality (w), which is 0,7, combination value of C1 and C2, which are 1,4 and 1,3, and the maximum iteration, which is 2500, and then it obtained the highest fitness value is on the seventh trial, which is 0,39949 with Root Mean Square Error (RMSE) value, which is 1,50319. The result from the highest fitness value is able to change the system from 27 arrangements to eight arrangements.
Keywords: initial moisture, fuzzy inference system, mamdani, Particle Swarm Optimization algorithm, rule base fuzzy choice
1. PENDAHULUAN
Pengolahan tanah yang baik menjadi salah
tanah dapat dilakukannya pengujian terhadap tanah. Pengujian terhadap tanah mempunyai berbagai parameter pendukung. Seperti pada
Laboratorium Tanah Balai Pengkajian
Teknologi Pertanian (BPTP) Jawa Timur, terdapat 8 parameter yang digunakan untuk pengujian tanah. Salah satu parameter tersebut adalah kadar air (Balai Pengkajian Teknologi Pertanian Jawa Timur, 2010). Kelembapan tanah merupakan salah satu benda yang mengandung kadar air, karena kelembapan tanah merupakan banyaknya kandungan air yang terkandung di dalam tanah.
Pengujian parameter kelembapan tanah yang dilakukan oleh Laboratorium Tanah BPTP Jatim menggunakan bantuan alat yang bertujuan untuk mendapatkan data yang ideal. Akan tetapi alat asli yang digunakan untuk pengujian masih sederhana, seperti penggunaan serangkaian paku yang dialiri air ketika melakukan penyiraman untuk menghasilkan kelembapan tanah yang ideal. Alat yang tidak bisa bekerja secara otomatis tersebut menjadi nilai minus tersendiri, karena kelembapan tanah yang dihasilkan di pengujian tersebut dapat tidak sesuai jika diterapkan di lapangan.
Saat ini di Laboratorium Benih BPTP Jatim sedang dikembangkan alat yang diciptakan oleh peneliti terdahulu, Muhammad Rifqi Maulana (2017) yaitu alat siram otomatis berdasarkan sensor kelembapan tanah untuk menentukan kebutuhan volume air dalam tanah. Untuk mendapatkan hasil kelembapan tanah yang optimal, maka dilakukan pengujian tanah untuk mendapatkan data. Data hasil pengujian berupa kumpulan amatan kebutuhan volume air berdasarkan kelembapan tanah. Data tersebut memuat tiga variabel, antara lain adalah kelembapan awal tanah, lama waktu penyiraman dan volume air.
Dari permasalahan tersebut, penelitian ini akan menyelesaikan permasalahan tersebut dengan komputasi cerdas yang nantinya dapat diterapkan pada alat pengukur kelembapan tanah yang sudah dikembangkan oleh penelitian terdahulu. Alat pengukur kelembapan tanah tersebut akan melakukan penyiraman air pada lahan berdasarkan volume air sehingga dapat bekerja secara otomatis. Peneliti akan melakukan optimasi pada pemilihan aturan pada
Fuzzy Inference System Mamdani menggunakan algoritme Particle Swarm Optimization untuk menentukan banyaknya volume air pada tanaman tomat. Namun pada penelitian ini, berfokus pada komputasi cerdasnya yang akan
mengolah hasil sensor kelembapan tanah untuk
menentukan banyaknya volume air
menggunakan suatu metode.
Fuzzy Ineference System Mamdani sangat fleksibel pada perubahan dan ketidakpastian masalah (Hidayat, et al., 2014)
, s
ehingga Fuzzy Ineference System Mamdani ini sangat cocok untuk menentukan waktu yang paling optimal dengan kondisi yang tidak pasti. Fuzzy Ineference System Mamdani dapat melakukanpenalaran seperti bagaimana manusia
melakukan penalaran dengan nalurinya. Metode
fuzzy sendiri mempunyai 2 faktor yang dapat mempengaruhi kinerjanya, yaitu aturan dan derajat keanggotaannya (Esmin & Torres, 2007), sehingga untuk mendapatkan kinerja
yang optimal, aturan dan derajat
keanggotaannya perlu ditentukan dengan tepat. Pada penelitian ini hanya berfokus pada penentuan aturannya.
Permasalahan
optimasi
secara
matematis dapat dilakukan menggunakan
algoritme
Particle Swarm Optimization.
Algoritme Particle Swarm Optimization (PSO) adalah metode pencarian nilai optimal dengan mengadopsi pola hewan seperti sekelompok burung yang sedang mencari makan. Apabila terdapat seekor burung yang lebih dulu menemukan makanan, maka akan memberitahu kepada burung burung yang lain. Hal tersebut menunjukkan bahwa algoritme PSO dapat mencari solusi secara acak dari suatu kumpulan yang setiap partikelnya berkaitan dengan posisi dan kecepatan dalam melakukan pencarian baru berdasarkan perilakunya.
2. LANDASAN TEORI
2.1 Kelembapan Tanah
Kelembapan tanah atau yang bisa juga disebut sebagai lengas tanah merupakan air yang mengisi seluruh atau sebagian ruang pori - pori dalam tanah. Menurut Suyono dan Sudarmadil (1997) menyatakan bahwa kelembapan tanah kelembapan tanah sangat dinamis, hal ini disebabkan oleh penguapan melalui permukaan tanah, transparansi dan perkolasi. Kapasitas penyimpanan tanah tergantung pada tekstur, kedalaman dan struktur tanah.
2.3 Volume Air Dalam Tanah
utama
pembentuk
protoplasma.
Air
membantu menghasilkan hidrogen ketika
proses fotosintesis. Volume air yang tinggi
membuat aktivitas fisiologis pada tumbuhan
menjadi tinggi sedangkan volume air yang
rendah
membuat
aktivitas
fisiologis
tumbuhan menjadi rendah. Air juga dapat
menjaga suhu pada tanaman
(Noggle, 1983)
. Kelembapan air merupakan salah satu bentuk dari persediaan air dalam tanah yang dipengaruhi oleh besarnya volume air yang disiramkan ke tanah atau pengaruh curah hujan. Pemberian air terhadap tanah memiliki tujuan antara lain untuk menjaga dan meningkatkan kelembapan tanah agar tetap optimal.2.4 Logika Fuzzy
Profesor Lotfi A. Zadeh dari Universitas California tahun 1965, seorang guru besar di University of California, Berkeley, Amerika Serikat adalah seseorang yang pertama kali memperkenalkan konsep logika fuzzy. Dasar logika fuzzy adalah teori himpunan fuzzy. Pada teori himpunan fuzzy, peranan derajat keanggotaan sebagai penentu keberadaan elemen dalam suatu himpunan sangat penting. Nilai keanggotaan atau derajat keanggotaan menjadi ciri utama dalam penalaran dengan logika fuzzy tersebut (Kusumadewi & Purnomo, 2004).
2.5 Himpunan Fuzzy
Himpunan merupakan suatu kumpulan atau koleksi objek – objek yang mempunyai kesamaan sifat tertentu (Susilo, 2006).
Fungsi keanggotaan diartikan sebagai berikut: Jika X adalah himpunan semesta, maka fungsi keanggotaan µA (fungsi keanggotaan A pada X) yang diartikan oleh himpunan fuzzy A memiliki ketentuan berikut:
µA: X → [0,1] (1)
Di mana [0,1] merupakan interval bilangan real dari nol sampai dengan satu. Dua himpunan A dan B dinyatakan sama jika dan hanya jika
µA(x) = µB(x). Jika µA(x) bernilai satu, menunjukkan x adalah anggota penuh dari himpunan fuzzy A. Sementara nilai antara nol hingga satu menunjukkan bahwa x merupakan anggota dari himpunan fuzzy A secara parsial.
2.6 Fuzzy Inference System Mamdani
Fuzzy Inference System adalah sebuah sistem penarikan kesimpulan dari kumpulan-kumpulan kaidah fuzzy, kesimpulan yang diambil dapat berupa input nilai eksak maupun
Rules dalam kaidah fuzzy. Metode mamdani
dikenal juga sebagai metode Max-Min
(Kusumadewi & Purnomo, 2004). Metode Max-Min ini diperkenalkan pada tahun 1975 oleh Ebrahim Mamdani. Dalam penggunaan metode mamdani, prosesnya terdiri dari beberapa tahapan, antara lain:
1. Pembentukan himpunan fuzzy
Dalam tahap pertama ini, menentukan terlebih dulu semua variable yang terkait dalam proses yang akan ditentukan. Variabel input
maupun variabel output dibagi menjadi satu atau lebih himpunan fuzzy.
2. Aplikasi fungsi implikasi
Pada tahap ini basis aturan disusun. Basis aturan yang dimaksud adalah aturan-aturan
berupa implikasi-implikasi fuzzy yang
menyatakan relasi antara variabel input dengan variabel output. Fungsi implikasi yang digunakan pada metode mamdani adalah Min.
3. Komposisi aturan
Aturan fuzzy berisi pernyataan-pernyataan logika fuzzy atau fuzzy statement yang berbentuk pernyataan IF-THEN. Pada metode mamdani, komposisi aturan yang digunakan adalah Max, yaitu solusi himpunan fuzzy yang diperoleh dengan cara mengambil nilai maksimum pada aturan. Kemudian nilai maksimum tersebut
untuk memodifikasi daerah fuzzy dan
mengaplikasikannya ke output dengan
menggunakan operator OR (gabungan).
Misalkan ada 3 aturan (proposisi) sebagai berikut:
[R1] IF Kuota Penerimaan RENDAH And
Peminat NAIK THEN Pendaftar
BERTAMBAH;
[R2] IF Kuota Penerimaan STANDAR THEN Pendaftar NORMAL;
[R3] IF Kuota Penerimaan TINGGI AND
Peminat TURUN THEN Pendaftar
BERKURANG;
4. Penegasan (defuzzifikasi)
Menurut Kusumadewi (2004) input dari proses defuzzifikasi adalah suatu himpunan
fuzzy yang diperoleh dari komposisi aturan-aturan fuzzy, sedangkan output yang dihasilkan merupakan suatu bilangan pada domain himpunan fuzzy dalam range tertentu, maka harus diambil suatu nilai tertentu sebagai output.
Metode yang digunakan saat melakukan proses defuzzifikasi adalah:
a. Metode Centroid
Pada metode Centroid menghasilkan solusi yang didapatkan dari hasil jumlah momen dibagi dengan jumlah luas pada daerah baru yang
Proses algoritme Particle Swarm
Optimization diinspirasi oleh perilaku sosial dari binatang, seperti sekawan burung dan sekelompok ikan dalam suatu gerombolan (swarm) (Sevkli & Guner, 2006).
Particle Swarm Optimization (PSO) merupakan salah satu teknik optimasi yang memiliki kesamaan dengan Genetic Algorithm, yaitu dimulai dengan membangkitkan populasi secara acak. Namun berbeda dengan Genetic Algorithm, PSO tidak memiliki operator evolusi, yaitu crossover dan mutasi. Selain itu, setiap partikel di dalam PSO juga berhubungan dengan suatu kecepatan. Partikel-partikel tersebut bergerak melalui penelusuran ruang dengan
kecepatan yang dinamis berdasarkan perilaku historisnya. Oleh karena itu, partikel-partikel mempunyai kecenderungan untuk bergerak ke ruang penelusuran yang lebih baik setelah melewati proses penelusuran sebelumnya.
b. Inisialisasi posisi terbaik partikel sampai posisi awalnya
pi (0) = xi (0) (5)
c. Hitung nilai fitness dari masing-masing partikel dan bila f(xj(0)) ≥ f(xi(0)) Ɐ i ≠ j maka inisialisasi global best adalah
g = xj (0) (6)
2. Sampai kriteria terpenuhi, ulangi langkah berikut:
a.
Ubah kecepatan partikel sesuai dengan ekuasi pada persamaan sebagai berikut:vi (t+1) = vi(t) + C1 (pi– xi(t)) R1+C2 (g-xi(t)) R2 (7)
b.
Ubah posisi partikel sesuai dengan ekuasi pada persamaan sebagai berikut:xi(t+1) = xi(t)+vi(t+1) (8)
c.
Evaluasi nilai fitness partikelf(xi(t+1)) (9) dijadikan sebagai variabel g.
2.8 Binary Particle Swarm Optimization
mengusulkan versi modifikasi dari PSO yang disebut Binary Particle Swarm Optimization
(BPSO) yang dapat digunakan untuk
memecahkan masalah optimasi fungsi diskrit. Perbedaan utama dari standar PSO dan BPSO adalah pada interpretasi dari kecepatan.
Pada BPSO kecepatan dibatasi dalam kisaran [0,1]. Persamaan dari kecepatan seperti persamaan (12).
𝑣′
𝑖𝑗(𝑡) = 𝑠𝑖𝑔((𝑡)) =1+𝑒−𝑣𝑖𝑗(𝑡)1 (12)
Persamaan (12) digunakan untuk
memperbarui vektor kecepatan partikel. Posisi baru partikel diperoleh dengan menggunakan persamaan 13.
𝑥𝑖𝑗(𝑡 + 1) = {1 , 𝑖𝑓 𝑟0 , 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒 𝑖𝑗< 𝑠𝑖𝑔(𝑣𝑖𝑗(𝑡 + 1))
3. METODE PENGUMPULAN DATA
Data yang dikumpulkan adalah data kebutuhan volume air pada tanaman tomat. Data tersebut didapatkan dari hasil pengujian tanah secara langsung oleh Hendra Pratama Budianto (2017)dengan menggunakan alat siram otomatis yang dikembangkan oleh Muhammad Rifqi Maulana (2017). Pengujian tanah secara langsung tersebut dilakukan pada tanggal 10 November 2016 – 30 Januari 2017. Pengujian yang dilakukan oleh Hendra Pratama Budianto dan Muhamad Rifqi Maulana didampingi oleh pakar dari Laboratorium Tanah BPTP Jawa Timur.
Gambar 1. Alat Siram Otomatis Yang Digunakan Untuk Pengujian Tanah
Alat siram otomatis yang digunakan dalam pengujian tanah tersebut berdasarkan sensor kelembapan tanah. Pengambilan data dilakukan dengan cara mengukur beberapa sampel tanah
yang pada keadaan yang berbeda dimulai dari keadaan kering hingga keadaan basah. Kemudian, pada masing-masing sampel tersebut diukur dahulu kelembapan awal tanahnya dengan bantuan sensor kelembapan tanah pada alat yang digunakan. Setelah itu, diukur banyaknya air yang dibutuhkan dari
masing-masing sampel tanah hingga mencapai
kelembapan ideal tanaman tomat. Sehingga data yang dihasilkan berupa kumpulan amatan kelembapan tanah terhadap kebutuhan volume air yang didapatkan.
4. PERANCANGAN ALGORITME
Pada penelitian ini permasalahan yang ingin di selesaikan adalah memilih aturan fuzzy
menggunakan algoritme optimasi yaitu
algoritme PSO. Diselesaikan berdasarkan 2 variabel masukan yaitu kelembapan awal dan lama waktu siram.
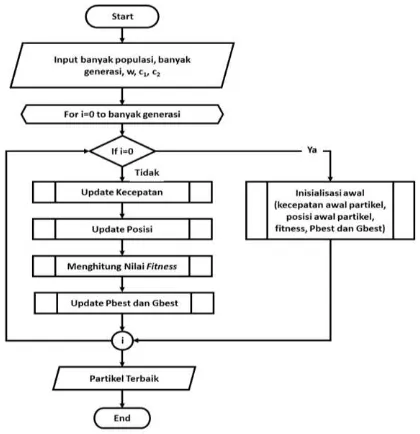
Rancangan algoritme PSO pada penelitian ini yaitu setiap partikel berisi 27 indeks posisi. Indeks posisi tersebut merepresentasikan 27 aturan yang telah di tentukan. Setiap satu indeks posisinya menghitung 30 data kebutuhan volume air terhadap kelembapan tanah pada tanaman tomat. Diagram alir algoritme PSO dapat dilihat pada gambar 2.
Gambar 2. Diagram Alir Algoritme Particle Swarm Optimization
5.1 Pengujian dan Analisis Jumlah Partikel
Pengujian jumlah partikel atau yang bisa disebut dengan pengujian ukuran populasi bertujuan untuk mendapatkan jumlah partikel dengan nilai fitness terbaiknya. Pengujian jumlah populasi ini dilakukan sebanyak lima kali percobaan dengan jumlah partikel 50 sampai 300 dengan kelipatan 50. Selain itu ada beberapa parameter lain sebagai masukan untuk menguji jumlah partikel yaitu nilai bobot inersia, nilai C1
dan C2, dan jumlah iterasi maksimal. Masing-masing nilai parameter pendukung yang di masukan antara lain nilai bobot inersia (w)
adalah 1,00, nilai C1 dan C2 adalah 2,00, dan jumlah iterasi maksimal adalah 1500. Nilai parameter tersebut akan digunakan untuk mengukur semua jumlah partikel. Sehingga hasil pengujian ditunjukkan oleh Tabel 1 dan Gambar 3.
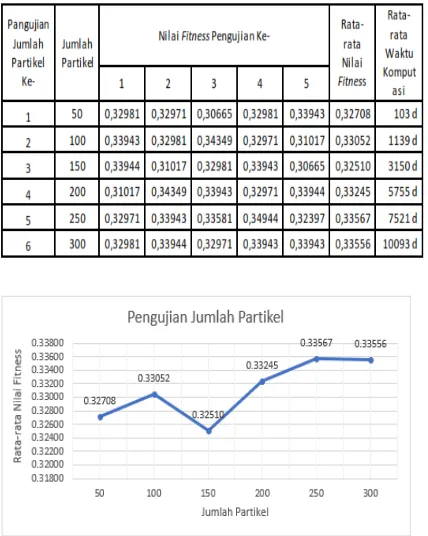
Tabel 1. Hasil Pengujian Jumlah Partikel
Gambar 3. Grafik Hasil Pengujian Jumlah Partikel
Dari hasil pengujian pada Tabel 1 dan Gambar 3 dapat dilihat rata-rata nilai fitness
terbaik dimiliki oleh jumlah partikel sebanyak 250 partikel dengan nilai fitness sebesar 0,33567. Sedangkan rata-rata nilai fitness
terkecil dimiliki oleh jumlah partikel sebanyak 150 partikel dengan nilai fitness sebesar 0,32510. Pada jumlah partikel sebanyak 100 partikel, rata-rata nilai fitness-nya mengalami
kenaikan. Namun, pada jumlah partikel sebanyak 150 partikel, rata-rata nilai fitness-nya mengalami penurunan. Hal tersebut disebabkan karena dari lima kali pengujian menggunakan jumlah partikel sebanyak 150 partikel, terdapat 1 hasil pengujian yang memiliki nilai fitness
sangat kecil dibanding 4 hasil pengujian yang lainnya. Ketidakpastian mendapatkan partikel yang semakin optimal tersebut juga disebabkan karena pembangkitan nilai partikel ini secara
acak.
5.2 Pengujian dan Analisis Nilai Bobot Inersia (w)
Pengujian nilai bobot inersia (w) bertujuan untuk mendapatkan nilai w dengan nilai fitness
terbaiknya. Pengujian nilai w ini juga bertujuan untuk mendapatkan posisi partikel yang terbaik. Pengujian nilai w ini dilakukan sebanyak sepuluh kali percobaan dengan nilai w 1,45 sampai 0,9 dengan selisih 0,05. Selain itu ada beberapa parameter lain sebagai masukan untuk menguji nilai w yaitu jumlah partikel, nilai C1
dan C2, dan jumlah iterasi maksimal. Masing-masing nilai parameter pendukung yang di masukan antara lain jumlah partikel adalah 50, nilai C1 dan C2 adalah 2,00, dan jumlah iterasi maksimal adalah 1500. Nilai parameter tersebut akan digunakan untuk mengukur semua nilai w. Sehingga hasil pengujian ditunjukkan oleh Tabel 2 dan Gambar 4.
Gambar 4. Grafik Hasil Pengujian Nilai Bobot Inersia (w)
Dari hasil pengujian pada Tabel 2 dan Gambar 4 dapat dilihat rata-rata nilai fitness
terbaik dimiliki oleh nilai w adalah 0,7 dengan nilai fitness sebesar 0,36870. Sedangkan rata-rata nilai fitness terkecil dimiliki oleh nilai w adalah 0,5 dengan nilai fitness sebesar 0,33318. Pada Gambar 4 terjadi kenaikan dan penurunan nilai fitness yang diakibatkan pemberian nilai w mempengaruhi pencarian posisi terbaik oleh setiap partikel dalam keseluruhan iterasi di setiap kali proses PSO. Maka dapat disimpulkan dari hasil pengujian nilai w bahwa pengujian ini sangat mempengaruhi nilai fitness pada setiap kali percobaan. Semakin besar nilai w juga belum tentu mendapatkan nilai fitness yang semakin optimal dikarenakan tidak terlalu banyak peningkatan bahkan bisa saja menurun.
5.3 Pengujian dan Analisis Nilai C1 dan C2
Pengujian nilai 𝐶1 dan 𝐶2 bertujuan untuk mendapatkan nilai 𝐶1 dan 𝐶2 dengan nilai fitness
terbaiknya. Pengujian nilai 𝐶1 dan 𝐶2 ini juga bertujuan untuk mengatur keseimbangan antara komponen kognitif dan komponen sosial. Pengujian nilai 𝐶1 dan 𝐶2 ini dilakukan sebanyak sepuluh kali percobaan dengan kombinasi nilai 𝐶1-nya 0,2 sampai 2 dengan selisih sekitar 0,2 dan kombinasi nilai 𝐶2-nya 0,1 sampai 2 dengan selisih sekitar 0,3. Selain itu ada beberapa parameter lain sebagai masukan untuk menguji nilai 𝐶1 dan 𝐶2 yaitu jumlah partikel, nilai bobot inersia, dan jumlah iterasi maksimal. Masing-masing nilai parameter pendukung yang di masukan antara lain jumlah partikel adalah 50, nilai bobot inersia adalah 1,00, dan jumlah iterasi maksimal adalah 1500. Nilai parameter tersebut akan digunakan untuk mengukur semua nilai 𝐶1 dan 𝐶2. Sehingga hasil pengujian ditunjukkan oleh Tabel 3 dan Gambar 5.
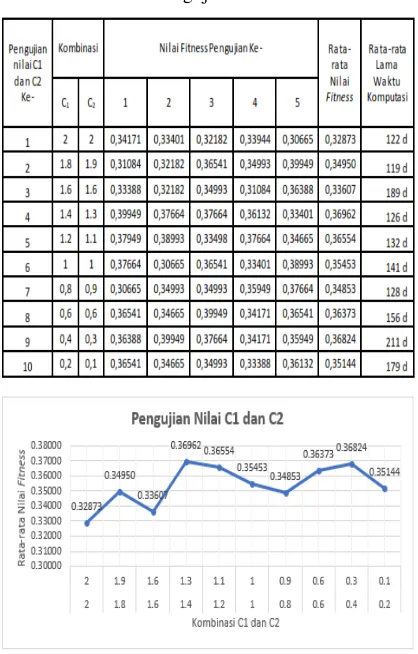
Tabel 3. Hasil Pengujian nilai 𝐶1 dan 𝐶2
Gambar 5. Grafik Hasil Pengujian Nilai 𝐶1 dan 𝐶2
Dari hasil pengujian pada Tabel 3 dan Gambar 5 dapat dilihat rata-rata nilai fitness
terbaik dimiliki oleh kombinasi nilai 𝐶1 adalah 1,4 dan nilai 𝐶2 adalah 1,3 dengan nilai fitness
sebesar 0,36962. Sedangkan rata-rata nilai
fitness terkecil dimiliki oleh kombinasi nilai 𝐶1
adalah 2 dan nilai 𝐶2 adalah 2 dengan nilai
fitness sebesar 0,32873. Pada Gambar 5 terjadi kenaikan dan penurunan nilai fitness yang diakibatkan pembangkitan nilai secara acak atau nilai random pada setiap kali proses particle swarm optimization.
5.4 Pengujian dan Analisis Jumlah Iterasi Maksimal
bobot inersia, dan nilai C1 dan C2. Masing-masing nilai parameter pendukung yang di masukan antara lain jumlah partikel adalah 50, nilai bobot inersia (w) adalah 1,00, dan nilai C1
dan C2 adalah 2,00. Nilai parameter tersebut akan digunakan untuk mengukur semua jumlah iterasi maksimal. Sehingga hasil pengujian ditunjukkan oleh Tabel 4 dan Gambar 6.
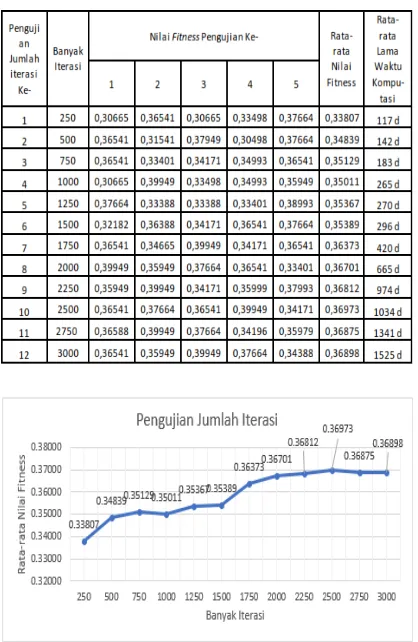
Tabel 4. Hasil Pengujian Jumlah Iterasi Maksimal
Gambar 6. Grafik Hasil Pengujian Jumlah Iterasi Maksimal
Dari hasil pengujian pada Tabel 4 dan Gambar 6 dapat dilihat rata-rata nilai fitness
terbaik dimiliki oleh jumlah iterasi maksimal sebanyak 2500 iterasi dengan nilai fitness
sebesar 0,36973. Sedangkan rata-rata nilai
fitness terkecil dimiliki oleh jumlah iterasi maksimal sebanyak 250 iterasi dengan nilai
fitness sebesar 0,33807. Dari grafik pada Gambar 6 dapat diketahui bahwa perubahan
pada jumlah iterasi maksimal sangat
berpengaruh terhadap besarnya fitness yang tercapai. Pengujian jumlah iterasi maksimal dengan fitness yang paling kecil dihasilkan oleh angka 250 iterasi, fitness yang kecil dipengaruhi oleh jumlah iterasi maksimal yang kecil juga
karena area pencarian yang dilakukan oleh algoritme PSO masih tergolong sempit. Sehingga dapat disimpulkan bahwa peningkatan jumlah iterasi seiring dengan peningkatan jumlah fitness. Namun pada titik tertentu mengalami penurunan karena area pencarian sudah menjauhi area optimal. Selain itu jumlah iterasi yang terlalu besar memerlukan waktu pencarian yang lebih panjang dan tidak menjamin solusi yang dihasilkan dapat lebih mendekati optimal.
5.5 Analisis Hasil Pengujian
Berdasarkan hasil dari pengujian parameter algoritme PSO, yaitupengujian jumlah partikel, nilai bobot inersia (w), nilai C1 dan C2, dan jumlah iterasi maksimaldidapatkan hasil terbaik dari masing-masing pengujian. Hasil terbaik tersebut antara lain jumlah partikelnya sebanyak 200 partikel, nilai bobot inersia (w) adalah 0,7, nilai C1 adalah 1,4 dan nilai C2 adalah 1,3, dan iterasi maksimalnya adalah 2500. Nilai parameter algoritme PSO yang telah didapat akan dijadikan sebagai input untuk mencari aturan pada fuzzy inference system mamdani yang telah dioptimasi. Aturan hasil optimasi tersebut nantinya akan digunakan untuk menghitung kebutuhan volume air dalam sistem penyiraman otomatis pada tanaman tomat. Setelah jumlah volume air didapatkan akan dihitung nilai eror yang didapatkan dari hasil
perhitungan menggunakan metode fuzzy
inference system Mamdani dengan rumus RMSE dan akan ditampilkan hasil fitness setelah optimasi menggunakan algoritme PSO yang digunakan sebagai akurasi sistem. Hasil perhitungan jumlah volume air dalam sistem penyiraman otomatis pada tanaman tomat dapat dilihat pada Gambar 7.
Gambar 7. Grafik Analisis Hasil Pengujian
inference system Mamdani dengan rumus RMSE dan hasil setelah dioptimasi menggunakan algoritme PSO. Hasil terbaik setelah dioptimasi adalah pengujian ke 7 dengan nilai fitness
terbesar yaitu 0,39949 dengan lama waktu komputasi selama 1263 detik. Pada pengujian ke 7 tersebut, nilai RMSE yang didapatkan adalah 1,50319.Dalam hal ini terlihat bahwa nilai eror menggunakan RMSE mengalami kenaikan dan penurunan. Dari hasil terbaik setelah dioptimasi tersebut, dapat diketahui aturan fuzzy inference system Mamdani yang terbaik untuk menghitung jumlah volume air dalam sistem penyiraman otomatis pada tanaman tomat.
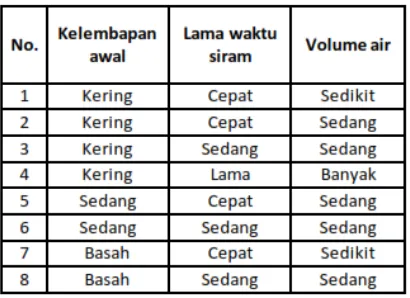
Tabel 5. Aturan Hasil Optimasi
Aturan fuzzy inference system Mamdani yang terpilih akan digunakan untuk menghitung kebutuhan volume air pada tanaman tomat. Setelah kebutuhan volume air didapatkan akan dihitung nilai eror yang didapat dari hasil
perhitungan menggunakan metode fuzzy
inference system Mamdani setelah dioptimasi menggunakan PSO.Pada Kebutuhan volume air setelah dioptimasi, nilai eror yang dihasilkan sebesar 0,581. Hasil tersebut memperlihatkan bahwa nilai eror setelah metode fuzzy inference system Mamdani diperoleh dari beberapa faktor lain seperti derajat keanggotaan yang belum optimal dan penentuan aturan yang belum sesuai
karena akan memengaruhi perhitungan
defuzzifikasinya. Sedangkan pada algoritme PSO nilai eror dapat diperoleh dari beberapa faktor yaitu terdapat faktor bilangan random
yang dibangkitkan setiap kali pemberian nilai partikel yang menginterpretasikan aturan yang
digunakan, menghitung kecepatan dan
menghitung pergerakan posisi partikel pada algoritme particle swarm optimization. Bilangan tersebut belum tentu sama antara proses pemilihan aturan fuzzy inference system
Mamdani satu dengan yang lainnya, sehingga hasil fitness dan aturan yang dihasilkan berbeda pula.
6. KESIMPULAN
Berdasarkan hasil dan analisis Pengujian, didapatkan kesimpulan antara lain:
1. Ketika melakukan pemilihan aturan fuzzy inference system Mamdani menggunakan algoritme PSO, terdapat beberapa parameter yang mempengaruhi proses optimasi. Pada pengujian jumlah partikel didapatkan jumlah partikel optimal yaitu sebanyak 250 dengan nilai fitness sebesar 0,33567 dan lama waktu komputasi sistem selama 7521 detik. Pada pengujian nilai bobot inersia didapatkan nilai bobot inersia optimal adalah 0,7 dengan nilai
fitness sebesar 0,36870 dan lama waktu komputasi sistem selama 189 detik. Pada pengujian nilai C1 dan C2 didapatkan nilai
C1 dan C2 optimal adalah C1 1,4 dan C2 1,3 dengan nilai fitness sebesar 0,36962 dan lama waktu komputasi sistem selama 126 detik. Dan pada pengujian jumlah iterasi maksimal didapatkan iterasi optimal yaitu 2500 dengan nilai fitness 0,36973 dan lama waktu komputasi sistem selama 1034 detik.
2. Dari beberapa kali percobaan, didapatkan nilai akurasi sistem yang berbeda satu sama lain yang dapat dilihat dari nilai fitness yang dihasilkan. Nilai akurasi sistem yang berbeda disebabkan karena aturan yang terpilih yang dimiliki oleh setiap partikel di setiap iterasinya juga berbeda. Selain itu, hal tersebut terjadi dikarenakan terdapat faktor bilangan acak (random) yang dibangkitkan
setiap kali menghitung kecepatan
pergerakan partikel dalam proses algoritme PSO. Dapat disimpulkan bahwa setelah metode fuzzy inference system Mamdani dioptimasi menghasilkan nilai eror 0,581. Hal ini membuktikan bahwa metode fuzzy inference system Mamdani yang telah dioptimasi algoritme PSO dapat diterapkan
dalam menyelesaikan permasalahan
menentukan kebutuhan volume air pada tanaman tomat.
7. SARAN
Saran yang dapat digunakan untuk
1. Penambahan variabel masukan tidak hanya kelembapan awal tanah dan lama waktu siram saja, dapat ditambahkan beberapa parameter lain seperti debit keran, suhu dan variabel lainnya yang mendukung proses penanaman tanaman. Penambahan variabel masukan dapat menambah jumlah aturan
fuzzy, sehingga dengan jumlah aturan yang semakin banyak mungkin saja akan mendapatkan hasil yang lebih optimal lagi.
2. Penelitian berikutnya disarankan tidak terfokus hanya pada satu tanaman saja melainkan semua jenis tanaman yang sesuai dengan pembibitan di Balai Teknologi Pertanian Jawa Timur (BPTP Jatim). Sehingga dapat membantu BPTP dalam pembibitan semua jenis tanaman yang ada.
8. DAFTAR PUSTAKA
Balai Pengkajian Teknologi Pertanian Jawa Timur. (2010). Laboratorium Tanah.
Dipetik Juli 20, 2017, dari
http://jatim.litbang.pertanian.go.id/ind/ Budianto, H. P., Setiawan, B. D., & Adikara, P.
P. (2017). Algoritme Genetik untuk Optimasi Pembentukan Fungsi Regresi Linier dalam Menentukan Kebutuhan Volume Air Penyiraman Tanah. Jurnal Pengembangan Teknologi Informasi dan Ilmu Komputer , 1(9), 748-753.
Esmin, A. A., & Torres, G. L. (2007). Evolutionary computation based fuzzy membership functions optimization.
IEEE International Conference on Systems, Man and Cybernetics.
Hidayat, H. R., Putri, R. R., & Mahmudy, W. F. (2014). Sistem Pakar Penentuan
Kebutuhan Pembelajaran Bahasa
Inggris dengan Metode Fuzzy Inference System Mamdani. Repository Jurnal Mahasiswa PTIIK Universitas Brawijaya, 4(3).
Kusumadewi, S., & Purnomo, H. (2004).
Aplikasi Logika Fuzzy untuk Pendukung Keputusan. Jakarta: Graha Ilmu.
Marini, F., & Walczak, B. (2015). Particle Swarm Optimization (PSO). IEEE Chemometrics and Intelligent Laboratory Systems, 13.
Muhammad Rifqi Maulana, M. H. (2017). Penerapan Metode Logika Fuzzy Untuk
Alat Monitoring Kelembapan Tanah Pada. Jurnal Pengembangan Teknologi Informasi dan Ilmu Komputer, 1(1), x-x. Noggle, G. d. (1983). Introduction Plant Physiology (2nd ed.). New Jersey: Prentice Hall, Inc, Englewood Clifts. Sevkli, M., & Guner, A. R. (2006). Acontinuous
Particle Swarm Optimization for Uncapacitated Facility Location Problem. In Ant Colony Optimization and Swarm Intelligence (pp. 4150:316-323). Lecture Notes in Computer Science.
Susilo, F. (2006). Himpunan dan Logika Kabur Serta Aplikasinya. Yogyakarta: Graha Ilmu.
Suyono, & Sumardil. (1997). Hidrologi Dasar.