APLIKASI TEOREMA GREEN PADA BIDANG DALAM MENGHITUNG LUAS SEGI-n DENGAN BANTUAN MATLAB SKRIPSI. Diajukan untuk Memenuhi Salah Satu Syarat

APLIKASI TEOREMA GREEN PADA BIDANG DALAM MENGHITUNG LUAS SEGI-𝒏 DENGAN BANTUAN MATLAB

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Pendidikan

Program Studi Pendidikan Matematika

Disusun Oleh:

Michael Bobby Christian 141414022

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

i

APLIKASI TEOREMA GREEN PADA BIDANG DALAM MENGHITUNG LUAS SEGI-𝒏 DENGAN BANTUAN MATLAB

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Pendidikan

Program Studi Pendidikan Matematika

Disusun Oleh:

Michael Bobby Christian 141414022

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

ii

SKRIPSI

APLIKASI TEOREMA GREEN PADA BIDANG DALAM MENGHITUNG LUAS SEGI-𝒏 DENGAN BANTUAN MATLAB

Oleh:

Michael Bobby Christian 141414022

Disetujui oleh: Dosen Pembimbing

iii

SKRIPSI

APLIKASI TEOREMA GREEN DALAM MENGHITUNG LUAS SEGI-𝒏

DENGAN BANTUAN MATLAB

Dipersiapkan dan disusun oleh:

Michael Bobby Christian 141414022

Telah dipertahankan di depan panitia penguji Pada tanggal 8 Mei 2019

dan dinyatakan memenuhi syarat

Susunan Panitia Penguji

Nama Lengkap Tanda Tangan

Ketua : Dr. Marcellinus Andy Rudhito, S.Pd. ... Sekretaris : Beni Utomo, M.Sc. ... Anggota I : Beni Utomo, M.Sc. ... Anggota II : Cyrenia Novella Krisnamurti, M.Sc. ... Anggota III : Dominukus Arif Budi Prasetyo, M.Si. ...

Yogyakarta, 8 Mei 2019

Fakultas Keguruan dan Ilmu Pendidikan Universitas Sanata Dharma

Dekan,

iv

HALAMAN PERSEMBAHAN

Kupersembahkan untuk:

Tuhan dan Allahku Yesus Kristus

Bapa Yoseph dan Bunda Maria

Papahku Hendrik dan mamahku Seravina

Almamater: Universitas Sanata Dharma Yogyakarta

v

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 8 Mei 2019 Peneliti

vi

LEMBAR PERNYATAAN PERSETUJUAN

PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma: Nama : Michael Bobby Christian

NIM : 141414022

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah yang berjudul:

APLIKASI TEOREMA GREEN DALAM MENGHITUNG LUAS SEGI-𝑵

DENGAN BANTUAN MATLAB

Dengan demikian saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelolanya dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikan di internet atau media lain untuk kepentingan akademis tanpa meminta ijin dari saya maupun memberikan royalty kepada saya selama tetap mencantumkan nama saya sebagai peneliti.

Dengan pernyataan ini saya buat dengan sebenarnya Yogyakarta, 8 Mei 2019

Yang menyatakan

vii

ABSTRAK

Michael Bobby Christian. 2019. Aplikasi Teorema Green pada Bidang dalam Menghitung Luas Segi-𝒏 dengan Bantuan MATLAB. Skripsi. Program Studi

Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma, Yogyakarta.

Aplikasi Teorema Green merupakan salah satu teorema dalam kalkulus vektor yang mengkaji bagaimana cara menghitung luas yang batas daerahnya merupakan kurva tertutup dan sederhana. Teorema tersebut dapat diterapkan pada bangun persegi panjang yang merupakan kurva tertutup dan sederhana. Perluasan atau akibat teorema Green pada bidang dapat digunakan untuk menghitung pendekatan luas daerah lingkaran satuan sebagai konsep limit.

Metode yang diterapkan dalam penelitian ini adalah studi kasus yang mempelajari integral garis untuk menghitung luas daerah dikaji dengan akibat teorema Green pada bidang yang dilakukan secara analitik sehingga dapat digunakan untuk menghitung luas segi-𝑛 dengan nilai n yang semakin besar. Luas lingkaran satuan didekati secara numerik yakni data luas dari segi-𝑛 yang dibuat. Langkah-langkah penelitian ini diawali dengan menemukan persamaan yang dapat digunakan untuk menghitung luas daerah segi-𝑛, segi-𝑛 yang dibuat adalah segi-𝑛 beraturan dan tak beraturan yang dibuat di luar dan di dalam lingkaran satuan. Selanjutnya menyusun program dengan bantuan MATLAB untuk menghitung dan memunculkan visualisasinya. Langkah berikutnya menghitung luas daerah segi-𝑛 untuk 𝑛 = 4, 8, 16, 32, 64, 128, 256, 512, dan 1024, kemudian data luas daerah tersebut akan dibandingkan dengan luas daerah lingkaran satuan yaitu 𝜋, dan memastikan bahwa program yang dibuat dapat berjalan dengan baik untuk semua nilai 𝑛.

Hasil penelitian menunjukkan, bahwa luas segi-𝑛 beraturan dan tak beraturan dengan menggunakan akibat teorema Green pada bidang untuk menghitung luas daerah dengan bantuan software MATLAB dapat digunakan dengan baik untuk semua nilai 𝑛. Luas segi-𝑛 yang dicari dengan nilai 𝑛 semakin besar yang dibuat di luar atau di dalam lingkaran satuan, setelah diamati luasannya semakin mendekati luas dari lingkaran satuan. Program yang disusun mampu menunjukkan visualisasi daerah segi-𝑛 beraturan dan tak beraturan yang dibuat di luar dan di dalam lingkaran satuan untuk semua nilai 𝑛 yang diinginkan. Program yang dihasilkan ini juga dapat digunakan untuk membantu dalam memahami pembelajaran konsep limit yaitu luas segi-𝑛 akan konvergen ke suatu nilai dalam kasus ini konvergen keluas daerah lingkaran satuan.

viii

ABSTRACT

Michael Bobby Christian. 2019. The Application of Green’s Theorem in Plane Geometry for Calculating The Area of Polygon by Using MATLAB. Thesis. Mathematics Education Study Program, Department of Mathematics and Science Education, Faculty of Teacher Training and Education, Sanata Dharma University, Yogyakarta.

The Green Theorem is one of the theorems in vector calculus which examines how to calculate the area where the boundary area is a closed curve and simple. The theorem can be applied to a rectangle which is a closed and simple curve. The extension or effect of the Green theorem on the field can be used to calculate the area of the unit circle area which is approach as a limit concept.

The method applied in this thesis was a case study that studies line integrals to calculate the area studied with the results of the Green theorem in an analytical field so that it can be used to calculate the n-faceted area. The area of the unit circle is approached numerically, which was the broad data from the n-aspect made. The writing steps began by finding a equation that could be used to calculate the area of the n-nodes, the n-nodes made are regular and irregular facets made outside and inside the unit circle. Then, compiling the program with MATLAB to calculate and bring up the visualization. The next step was to calculate the area of the nodes for n = 4, 8, 16, 32, 64, 128, 256, 512, and 1024, then the area data were compared to the area of the unit circle, which was π, and ensured that the program made could run well for all values n.

The results of the writing show, that the area of regular and irregular polygon using the results of the Green theorem in fields to calculate the area aided by MATLAB software can be used well for all values of n. The area of polygon is sought by the value of n wich is getting bigger which is made outside or inside the unit circle, after observing the area polygons it is getting closer to the area of the unit circle. The program was compiled to be able to show visualization of regular and irregular polygons made outside and inside a unit circle for all desired n values. The resulting program can also be used to assist in understanding limit concept learning, namely the polygons area will converge to a value in this case converging the area of the unit circle.

ix

KATA PENGANTAR

Puji dan syukur peneliti panjatkan kepada Tuhan Yang Maha Esa yang telah melimpahkan berkat dan rahmat-Nya sehingga peneliti dapat menyelesaikan skripsi yang berjudul “Aplikasi Teorema Green pada Bidang dalam Menghitung Luas Segi-𝑛 dengan Bantuan MATLAB” ini dengan baik. Skripsi ini disusun untuk memenuhi salah satu syarat memperoleh gelar Sarjana Pendidikan.

Banyak masalah yang menghambat dalam penelitian skripsi ini. Peneliti menyadiri skripsi ini tidak dapat selesai dengan baik tanpa adanya dukungan dan doa dari berbaga pihak. Oleh karena itu, pada kesempatan kali ini peneliti ingin menyampaikan ucapan terima kasih kepada:

1. Bapak Dr. Yohanes Harsoyo, S.Pd., M.Si. selaku dekan Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma Yogyakarta.

2. Bapak Beni Utomo, M.Sc. selaku Ketua Program Studi Pendidikan Matematika, juga selaku dosen pembimbing skripsi yang telah bersedia meluangkan waktu, tenaga, dan tiada lelah selalu mengingatkan peneliti penelitian skripsi di Universitas Sanata Dharma Yogyakarta.

3. Ibu Maria Suci Apriani, S.Pd., M.Sc. selaku dosen pembimbing akademik NIM genap yang telah bersedia memberikan masukan, semangat, dan refleksi selama peneliti menjalani kuliah di Program Studi Pendidikan Matematika Universitas Sanata Dharma Yogkyakarta.

4. Bapak, ibu, dan pastor dosen Program Studi Pendidikan Matematika Universitas Sanata Dharma yang telah mendidik peneliti selama kuliah di Pendidikan Matematika Universitas Sanata Dharma Yogyakarta.

5. Seluruh staff sekretariat JPMIPA yang telah membantu dalam hal administrasi, perpustakaan Universitas Sanata Dharma yang telah menyediakan buku-buku referensi yang menunjang perkuliahan selama berkuliah dan dalam penelitian skripsi, dan Laboran Micro Teaching Pendidikan Matematika yaitu mas Made Setianto yang terus mengingatkan penetili menyusun skripsi.

x

6. Kedua orangtua peneliti Papah Hendrikus Hendrik, Mamah Seravina Sumartini yang selalu mendukung dan juga adik peneliti Ignatius Benny Christian yang selalu mendukung peneliti.

7. Veronika Kania Anindita yang tiada lelah memberikan dukungan, semangat, dan menjadi pengingat agar tidak menyerah dalam penelitian skripsi.

8. Teman-teman seperjuangan Jonathan Wijaya, Fransiska Intan, Suhardy, Amdika Styadi, Joseph Wijaya, yang memberi semangat untuk mengerjakan skripsi.

9. Teman-teman Kos Asolole: Bagus, Favian, Yunus, Morgan, Hendra, Vander, Dimas, Bayu, Dominikus Bagus, dan Rizki yang menemani dalam penyusunan skripsi selama di kos.

10. Teman-teman kelas A dan bimbingan DPA Bu Maria NIM Genap 2014 Pendidikan Matematika Universitas Sanata Dharma Yogyakarta, yang telah memberikan pengalaman berharga yang tak dilupakan selama perkuliahan. 11. Teman-teman bimbingan skripsi Pak B: Anton, Titis, Dita, Desi, Hera, Meli,

yang sama-sama telah membuat Pak Beni kewalahan, tetap terus semangat. 12. Teman-teman Student Staff Humas dan Staff Humas Universitas Sanata

Dharma Yogyakarta yang memberikan pengalaman berharga bagi peneliti di akhir-akhir masa perkuliahan.

13. Semua pihak yang telah membantu peneliti selama kuliah dan selama menulis skripsi yang tidak dapat disebutkan satu persatu.

Peneliti mengucapkan terima kasih atas segala kritik dan saran yang membangun guna melengkapi skripsi ini. Semoga tulisan ini dapat bermanfaat dan memberikan wawasan yang lebih kepada setiap pembacanya.

Yogyakarta, 8 Mei 2019 Peneliti

xi

DAFTAR ISI

HALAMAN JUDUL ... i

HALAMAN PENGESAHAN ... iii

HALAMAN PERSEMBAHAN ... iv

PERNYATAAN KEASLIAN KARYA ... v

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ... vi

ABSTRAK ... vii

ABSTRACT ... viii

KATA PENGANTAR ... ix

DAFTAR ISI ... xi

DAFTAR TABEL ... xiii

DAFTAR GAMBAR ... xiv

DAFTAR SIMBOL ... xv BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 3 C. Batasan Masalah ... 3 D. Tujuan Penelitian ... 4 E. Manfaat Penelitian ... 4 F. Metode Penelitian ... 5 G. Sistematika Penelitian ... 6

BAB II KAJIAN PUSTAKA DAN DASAR TEORI ... 8

A. Sistem Koordinat Kartesius ℝ𝟐 ... 8

B. Koordinat Kutub ... 11

C. Lingkaran ... 13

D. Segi-𝒏 ... 18

E. Persamaan Garis Lurus ... 20

F. Konversi Sudut Radian Dalam Derajat ... 27

G. Turunan Parsial ... 28

H. Diferensial ... 29

xii

J. Luas Daerah Suatu Kurva... 31

K. Integral Kurva ... 33

BAB III AKIBAT TEOREMA GREEN PADA BIDANG ... 38

A. Teorema Green Pada Bidang ... 38

B. Kasus-kasus Pengaplikasian Teorema Green dalam Bidang ... 39

BAB IV PEMBAHASAN DAN HASIL ... 45

A. Formulasi Luas Segi-𝒏 Menggunakan Akibat Teorema Green Pada Bidang ... 46

B. Menghitung Luas Segi-𝒏 Menggunakan Akibat Teorema Green Pada Bidang dengan Menggunakan MATLAB ... 64

BAB V PENUTUP ... 85

A. Kesimpulan ... 85

B. Saran ... 87

DAFTAR PUSTAKA ... 88

xiii

DAFTAR TABEL

Tabel 4.1 Koordinat Titik Segiempat Beraturan di Luar Lingkaran Satuan. ... 66

Tabel 4.2 Pasangan Titik Segiempat Beraturan di Luar Lingkaran Satuan. ... 67

Tabel 4.3 Luas Segiempat Beraturan di Luar Lingkaran Satuan... 67

Tabel 4.4 Koordinat Titik Segiempat Beraturan di Dalam Lingkaran Satuan. .... 69

Tabel 4.5 Pasangan Titik Segiempat Beraturan di Dalam Lingkaran Satuan. ... 69

Tabel 4.6 Luas Segiempat Beraturan di Dalam Lingkaran Satuan. ... 70

Tabel 4.7 Koordinat Titik Segiempat Tak Beraturan di Dalam Lingkaran Satuan. ... 71

Tabel 4.8 Pasangan Titik Segiempat Beraturan di Dalam Lingkaran Satuan. ... 72

Tabel 4.9 Luas Segiempat Tak Beraturan di Dalam Lingkaran Satuan ... 72

Tabel 4.10 Koordinat Titik Segiempat Beraturan di Luar Lingkaran Satuan. ... 74

Tabel 4.11 Pasangan Titik Segiempat Beraturan di Luar Lingkaran Satuan. ... 74

Tabel 4.12 Luas Segiempat Beraturan di Luar Lingkaran Satuan... 75

Tabel 4.13 Koordinat Titik Segidelapan Beraturan di Dalam Lingkaran Satuan. 76 Tabel 4.14 Pasangan Titik Segiempat Beraturan di Dalam Lingkaran Satuan. ... 77

Tabel 4.15 Luas Segiempat Beraturan di Dalam Lingkaran Satuan ... 77

Tabel 4.16 Koordinat Titik Segiempat Tak Beraturan di Dalam Lingkaran Satuan. ... 79

Tabel 4.17 Pasangan Titik Segiempat Beraturan di Dalam Lingkaran Satuan. ... 80

Tabel 4.18 Luas Segiempat Tak Beraturan di Dalam Lingkaran Satuan ... 80

xiv

DAFTAR GAMBAR

Gambar 2. 1 Koordinat Kartesius ... 8

Gambar 2. 2 Kuadran Pada Bidang Koordinat... 9

Gambar 2. 3 Jarak Dua Titik Ruas Garis 𝐴𝐵 ... 10

Gambar 2. 4. Koordinat Kutub ... 11

Gambar 2. 5 Koordinat Kartesius ... 12

Gambar 2. 6 Lingkaran Berpusat di (0,0) ... 14

Gambar 2. 7 Lingkaran yang Berpusat di Titik A(𝑎, 𝑏) ... 15

Gambar 2. 8 Lingkaran Satuan ... 17

Gambar 2. 9 Persegi ... 18

Gambar 2. 10 Segitiga Sama Sisi ... 18

Gambar 2. 11 Segilima Tak Beraturan ... 18

Gambar 2. 12 Segienam Dalam Lingkaran ... 19

Gambar 2. 13 Segienam Luar Lingkaran ... 20

Gambar 2. 14 Garis 𝑙 ∥ Sumbu 𝑦 ... 20

Gambar 2. 15 Garis 𝑠 ∥ Sumbu 𝑥 ... 21

Gambar 2. 16 Garis 𝑙 yang Melewati Titik Asal Dan Sebuah Titik Tertentu ... 21

Gambar 2. 17 Garis 𝑙 yang Melewati Dua Titik ... 23

Gambar 2.18 Garis 𝑔 yang Melewati Suatu Titik dan Gradien Garis G Diketahui ... 25

Gambar 2. 19 Garis 𝑔 yang Berpotongan dengan Kedua Sumbu ... 26

Gambar 2. 20 Daerah di Atas Sumbu 𝑥 ... 32

Gambar 2. 21 Daerah di Bawah Sumbu 𝑥 ... 32

Gambar 2. 22 Daerah di Antara Dua Kurva ... 33

Gambar 2. 23 Partisi C dari [𝑎, 𝑏] ... 34

Gambar 2. 24 Luas Tirai Tegak Melengkung Sepanjang C ... 35

Gambar 3. 1 Ilustrasi Kasus I (Elips) ... 39

Gambar 3. 2 Daerah yang Dibatasi Oleh 𝑦 = 𝑥 dan 𝑦 = 𝑥2 ... 42

Gambar 3. 3 Daerah D yang dibatasi oleh Kurva C ... 43

Gambar 4. 1 Lingkaran Satuan ... 48

Gambar 4. 2 Segiempat di Luar Lingkaran Satuan ... 49

Gambar 4. 3 Segiempat ABCD di Dalam Lingkaran Satuan ... 51

Gambar 4. 4 Segidelapan ABCDEFGH ... 61

Gambar 4. 5 Segienambelas ABCDEFGH ... 62

Gambar 4. 6 Segiempat Beraturan di Dalam Lingkaran Satuan ... 66

Gambar 4. 7 Segiempat Beraturan di Dalam Lingkaran Satuan ... 68

Gambar 4. 8 Segiempat Tak Beraturan di Dalam Lingkaran Satuan ... 70

Gambar 4. 9 Segidelapan Beraturan di Dalam Lingkaran Satuan ... 73

Gambar 4. 10 Segidelapan Beraturan di Dalam Lingkaran Satuan ... 75

xv

DAFTAR SIMBOL

ℝ2 : Ruang Dimensi Dua Atas Semua Bilangan Real 𝑑(𝐴𝐶̅̅̅̅) : Panjang Ruas Garis 𝐴𝐶

𝜃 : Nama Sudut

|𝑥 − 𝑦| : Nilai Mutlak dari 𝑥 Kurang 𝑦 𝑔||𝑙 : Garis 𝑔 Sejajar Garis 𝑙

‖𝑃‖ : Norma P 𝑚 : Gradien Garis

 

b a f x dx



: Integral Tentu Suatu Fungsi 𝑥 Dari 𝑎 Sampai 𝑏 Terhadap 𝑥

( , )

C

f x y ds



: Integral Kurva Fungsi 𝑓(𝑥, 𝑦) Atas Lintasan C R



: Integral Lipat Dua Atas Daerah R

𝐷_𝑥 : Notasi Turunan Terhadap Variabel Bebas 𝑥 𝑑𝑦 : Notasi Diferensial Suatu Fungsi

≈ : Nilai Pendekatan

𝜕 : Notasi Turunan Parsial

∆𝑥 : Perubahan Nilai 𝑥

∑ : Penjumlahan Suatu Barisan Bilangan

° : Satuan Derajat

|| : Notasi Menyatakan Kesamaan Panjang Dua Atau Lebih Ruas Garis

1

BAB I

PENDAHULUAN

A. Latar Belakang

Matematika kini bukanlah suatu hal yang asing bagi kita. Terlebih kini Matematika dapat dikatakan suatu kebutuhan utama. Permasalah matematika dapat diselesaikan melalui dua metode yakni secara analitik ataupun secara numerik. Secara analitik, kita menggunakan rumus dan teorema yang sudah baku dalam pelajaran Matematika. Contohnya, dalam menghitung luas persegi panjang dengan rumus 𝑙𝑢𝑎𝑠 = 𝑝 × 𝑙 dimana 𝑝 adalah panjang dari persegi panjang dan 𝑙 lebar persegi panjang, solusi yang didapatpun berupa jawaban eksak. Namun pada metode numerik, digunakan pendekatan (aproksimasi) dengan menyusun algoritma yang terprogram dengan banyak perulangan. Contohnya adalah mencari nilai terdekat dari bilangan irrasional seperti √7, 𝜋, dan 𝑒. Saat ini jika mencari luas suatu bangun dalam matematika merupakan permasalah yang masih sederhana atau dengan kata lain untuk masing-masing bentuknya telah tersedia formula-formulanya, namun apabila kita hendak menghitung luas daerah yang bentuknya lebih rumit atau misal menghitung luas daerah suatu kota atau bahkan pulau tidak ada formula yang diberikan yang dapat digunakan untuk menghitung luas daerahnya. Seperti halnya yang dilakukan oleh pemerintah dalam mencari luas daerah suatu kota, tanah warga, dsb. Penelitian skripsi ini mencoba menemukan sebuah cara untuk menghitung luas daerah yang juga dapat digunakan untuk membantu dalam pembelajaran konsep limit.

Salah satu bidang ilmu matematika yakni kalkulus. Kalkulus meliputi dua permasalahan berikut, yaitu kalkulus diferensial dan kalkulus integral yang saling berkaitan dengan teorema dasar kalkulus. Kalkulus merupakan awalan menuju pelajaran matematika lainnya yang lebih tinggi, seperti analisis matematika yang khusus mempelajari fungsi dan limit. Contohnya dalam buku kalkulus karya Purcell dan Steward mereka berdua mengawalinya dengan mengulas tentang limit. Purcell mengatakan bahwa salah satu yang mengarah pada konsep pembelajaran limit yaitu luas lingkaran yang didekati secara grafis oleh luas segi-𝑛 yang dibuat di dalam dan di luar lingkaran, yang akan konvergen ke suatu nilai yakni akan konvergen ke luas lingkaran tersebut.

Kalkulus vektor merupakan salah satu cabang kalkulus yang lebih lanjut, di dalamnya terdapat beberapa materi yang berkaitan untuk menghitung luas daerah adalah integral garis dan akibat teorema Green pada bidang. Nama Teorema Green didapat dari George Green yakni seorang ilmuwan otodidak Inggris (yang juga merupakan penemu kasus khusus Teorema Stokes dimensi dua). Teorema Green menyatakan hubungan antara integral garis yang dilakukan sepanjang kurva tertutup sederhana 𝐶 dan integral lipat dua pada daerah bidang 𝐷 yang dibatasi oleh 𝐶 dalam vektor. Guna menyatakan teorema Green digunakan perjanjian bahwa penyelusuran 𝐶 dengan arah berlawanan putaran jarum jam ini menunjukkan dalam teorema Green arah menjadi syarat penting dalam pengerjaannya. (Stewart, 1999: 543-544).

Akibat teorema Green pada bidang untuk menghitung luas daerah dilakukan secara analitik dan kemudian perhitungan pada penelitian ini akan

dikaji secara numerik dengan menggunakan bantuan software MATLAB. MATLAB merupakan suatu software pemograman yang cukup diminati kalangan matematikawan untuk memecahkan permasalahan numerik, karena MATLAB juga dapat menyajikan visulisasi dari masalah numerik yang dicari. Penelitian ini lebih difokuskan pada memanfaatkan akibat Teorema Green pada bidang; terutama dalam memecahkan permasalahan tentang menghitung luas segi-𝑛 yang nantinya dapat dimanfaatkan untuk memberikan pemahaman lebih dalam konsep limit.

B. Rumusan Masalah

Rumusan masalah dalam penelitian ini adalah:

1. Bagaimana cara menghitung luas segi-𝑛 dengan menggunakan akibat Teorema Green pada bidang untuk menghitung pendekatan luas lingkaran satuan?

2. Bagaimana penggunaan akibat Teorema Green pada bidang untuk menghitung luas suatu daerah dengan menggunakan MATLAB?

C. Batasan Masalah

Batasan-batasan masalah dalam penelitian ini adalah:

1. Menghitung luas daerah dengan integral garis yang dikaji dengan akibat teorema Green pada bidang.

2. Luas pada segi-𝑛 yang dibuat di luar dan di dalam lingkaran satuan 3. Pendekatan dilakukan dengan membuat dan menghitung luas dari

4. Software yang digunakan dalam membantu penelitian ini adalah

MATLAB.

D. Tujuan Penelitian

Tujuan penelitian yang ingin dicapai adalah:

1. Menganalisa cara menghitung luas segi-𝑛 dengan menggunakan akibat teorema Green pada bidang untuk menghitung luas sebagai pembelajaran konsep limit.

2. Menghitung luas suatu daerah pada segi-𝑛 dengan menggunakan MATLAB.

E. Manfaat Penelitian

Adapun manfaat dari penelitian ini adalah sebagai berikut: 1. Bagi Peneliti

Peneliti menambah pengetahuan mengenai Teorema Green, serta dapat membangun suatu program yang dapat membantu serta

mem-visual-kan pendekatan yang dilakukan dengan menggunanakan bantuan

MATLAB. 2. Bagi Pembaca

Pembaca dapat mengetahui bagaimana melakukan pendekatan luas lingakaran secara numerik dengan memanfaatkan akibat dari teorema Green, melalui MATLAB.

F. Metode Penelitian

Metode yang digunakan oleh peneliti dalam menyusun skripsi ini adalah metode studi pustaka, yakni peneliti membaca referensi-referensi yang berkaitan dengan segi-𝑛, teorema Green, lingkaran, dan MATLAB. Kemudian peneliti mencoba untuk memanfaatkan apa yang telah didapat kemudian mencoba membuat suatu program dalam MATLAB yang dapat digunakan dalam pengembangan berikutnya.

Langkah-langkah yang dilakukan dalam penelitian ini adalah:

1. Membaca berbagai referensi yang berkaitan dengan geometri analitik bidang, kalkulus diferensial, kalkulus integral, teorema Green, lingkaran, dan berbagai referensi lain yang dibutuhkan, serta menonton

tutorial dalam menggunakan MATLAB.

2. Melakukan pengakajian rumus dari akibat teorema Green pada bidang untuk menghitung luas daerah secara analitik.

3. Membuat segi-𝑛 beraturan yang dibuat di dalam dan di luar lingkaran satuan, serta segi-𝑛 tak beraturan yang dibuat di dalam dengan 𝑛 = 4, 8, 16, 32, sampai 1024.

4. Menemukan koordinat (𝑥, 𝑦) titik-titik sudut pada segi-𝑛 beraturan yang dibuat di luar dan di dalam lingkaran satuan serta segi-𝑛 tak beraturan yang dibuat di dalam lingkaran satuan.

6. Membuat program pada MATLAB sebagai alat bantu visual dalam proses penggambaran lingkaran satuan dan segi-𝑛 berurutan dan tak beraturan hingga membantu proses perhitungan.

7. Membandingkan luas masing-masing segi-𝑛 beraturan dengan luas lingkaran satuan.

8. Menyusun hasil penelitian.

G. Sistematika Penelitian

Tujuan akhir penelitian skripsi ini yaitu untuk mengetahui bahwa luas lingkaran satuan dapat didekati secara numerik dengan menggunakan segi-𝑛 beraturan. Agar penelitian penelitian ini tersusun secara sistematis, maka peneliti memberikan sistematika penelitian sebagai berikut:

BAB I PENDAHULUAN

Adapun pada bab I berisikan latar belakang, rumusan masalah, batasaan masalah, tujuan penelitian, manfaat penelitian, metode penelitian, dan sistematika penelitian.

BAB II LANDASAN TEORI

Adapun pada bab II berisikan sistem koordinat kartesius, jarak dua titik pada bidang, segi-𝑛, persamaan garis lurus, pengertian luas, lingkaran satuan, turunan parsial, dan integral garis. Pada bab ini menjadi batasan materi yang digunakan dalam penelitian ini.

Penelitian ini akan melakukan pendekatan luas lingkaran satuan secara numerik oleh luas segi-𝑛 yang dibuat di luar dan di dalam lingkaran satuan. Selanjutnya untuk menghitung luas segi-𝑛 tersebut

dengan menggunakan integral garis yang dikaji dengan akibat teorema Green pada bidang yang dilakukan secara analitik. Penelitian skripsi ini merupakan lanjutan dari penelitian sebelumnya yang juga menghitung luas segi-𝑛 dengan akibat teorema Green pada bidang menggunakan

software Microsoft Excel untuk segi-𝑛 yang beraturan, sedangkan dalam skripsi ini akan dihitung luas daerah segi-𝑛 beraturan dan tak beraturan yang dibuat di luar dan di dalam lingkaran satuan dengan mengunakan MATLAB dan memanfaatkan fitur GUI.

BAB III TOEREMA GREEN PADA BIDANG

Adapun pada bab III berisikan Teorema Green pada bidang dan kasus-kasus pengaplikasian Teorema Green dalam bidang.

BAB IV HASIL DAN PEMBAHASAN

Adapun pada bab IV berisikan formulasi luas segi-𝑛 beraturan menggunakan akibat Teorema Green pada bidang, dan formulasi luas segi-𝑛 menggunakan akibat Teorema Green pada bidang dengan menggunakan MATLAB.

BAB V KESIMPULAN DAN SARAN

Adapun pada bab V berisikan kesimpulan dan saran dari penelitian skripsi ini.

8

BAB II

KAJIAN PUSTAKA DAN DASAR TEORI

A. Sistem Koordinat Kartesius ℝ𝟐 1. Sistem Koordinat Kartesius ℝ2

Sistem koordinat kartesius di dimensi dua (ℝ2_{) atau bidang} terdiri dari dua garis yang saling tegak lurus dan berpotongan di titik 𝑂(0,0) yang disebut titik asal (Suarsana, 2014). Garis yang mendatar (horizontal) dinamakan sumbu 𝑥. pada sumbu 𝑥 dari titik 𝑂 ke kanan disebut arah positif atau sumbu 𝑥 positif. Sedangkan dari titik 𝑂 ke kiri dikatakan arah negatif atau sumbu 𝑥 negatif. Garis yang tegak (vertikal) dinamakan sumbu 𝑦. Pada sumbu 𝑦, dari titik 𝑂 ke atas disebut arah positif atau sumbu 𝑦 positif. Sedangkan dari titik 𝑂 ke bawah dikatakan arah negatif atau sumbu 𝑦 negatif. Letak titik-titik yang ada pada ℝ𝟐 dinyatakan dalam bentuk (𝑥, 𝑦). Gambar 2.1 menunjukkan titik 𝑃 pada koordinat kartesius.

Gambar 2. 1 Koordinat Kartesius

Sumber: Suarsana, 2014 𝑦 𝑥 𝑂 𝑃(𝑥, 𝑦) (𝑥, 0) (0, 𝑦)

Sebuah titik 𝑃 pada koordinat kartesius dapat dinyatakan sebagai berikut 𝑃(𝑥, 𝑦), 𝑥 merupakan koordinat titik 𝑃 pada sumbu-𝑥 disebut absis, sedangkan 𝑦 merupakan koordinat dari titik 𝑃 pada sumbu-𝑦 disebut ordinat.

Sumbu koordinat pada bidang kartesius terbagi menjadi empat daerah yang disebut kuadran Suarsana (2014), seperti Gambar 2.2 di bawah ini:

Gambar 2. 2 Kuadran Pada Bidang Koordinat

Sumber: Suarsana, 2014

Keterangan:

Kuadran I, koordinat 𝑥 positif dan 𝑦 positif Kuadran II, koordinat 𝑥 negatif dan 𝑦 positif Kuadran III, korrdinat 𝑥 negatif dan 𝑦 negatif Kuadran IV, koordinat 𝑥 positif dan 𝑦 negatif 2. Jarak Dua Titik Pada Bidang

Menurut Suarsana (2014), jarak dua titik merupakan suatu besaran satuan panjang, yang terbentuk dari dua buah titik berbeda pada bidang, maka jarak antara kedua titik tersebut adalah panjang ruas garis

𝑂 𝑥 𝑦 Kuadran II (−, +) Kuadran I (+, +) Kuadran III (−, −) Kuadran IV (+, −)

yang menghubungkan kedua titik tersebut. Jarak Euclides yaitu perhitungan jarak dari 2 buah titik yang berdekatan.

Gambar 2. 3 Jarak Dua Titik Ruas Garis 𝐴𝐵̅̅̅̅

Sumber: Suarsana, 2014

Misalkan 𝐴(𝑥₁, 𝑦₁) dan 𝐵(𝑥₂, 𝑦₂) dua titik berbeda seperti pada Gambar 2.3, dengan 𝑥₁ ≠ 𝑥₂ dan 𝑦₁ ≠ 𝑦₂ selanjutnya 𝐶(𝑥₂, 𝑦₁). Selanjutnya Wernick (1968), melalui segitiga siku-siku ∆𝐴𝐶𝐵 dengan siku-siku di titik 𝐶 dengan menggunakan teorema Phytagoras untuk menghitung panjang ruas garis 𝐴𝐵̅̅̅̅, diperoleh:

𝑑(𝐴𝐶̅̅̅̅) = |𝑥₂− 𝑥₁| 𝑑(𝐵𝐶̅̅̅̅) = |𝑦₂− 𝑦₁| Kemudian 𝑑(𝐴𝐵̅̅̅̅)2 _{= 𝑑|𝐴𝐶̅̅̅̅|}2_{+ 𝑑|𝐵𝐶̅̅̅̅|}2 𝑑(𝐴𝐵̅̅̅̅)2 = (𝑥2− 𝑥1)2+ (𝑦2− 𝑦1)2 𝑑(𝐴𝐵̅̅̅̅)2 _{= √(𝑥} 2− 𝑥1)2+ (𝑦2− 𝑦1)2 Contoh 2.1:

Tentukan jarak antara titik 𝐴(1,4) dan titik 𝐵(−3,2)! 𝐵(𝑥2, 𝑦2)

(𝑥1, 𝑦1)

Penyelesaian: 𝑑(𝐴𝐵̅̅̅̅) = √(𝑥₂− 𝑥₁)2_{+ (𝑦} 2− 𝑦1)2 𝑑(𝐴𝐵̅̅̅̅) = √(−3 − 1)2_{+ (2 − 4)}2 𝑑(𝐴𝐵̅̅̅̅) = √(−4)2_{+ (−2)}2 𝑑(𝐴𝐵̅̅̅̅) = √16 + 4 𝑑(𝐴𝐵̅̅̅̅) = √20 = 2√5

Jadi, jarak antara titik 𝐴 dan titik 𝐵 adalah 2√5.

B. Koordinat Kutub

Koordinat kutub juga dapat digunakan untuk menentukan kedudukan suatu titik selain mengunakan koordinat kartesius. koordinat kutub dinyatakan dalam sebuah sinar garis dengan sumbu-𝑥 dan titik pangkalnya, sinar garis ini biasanya digambar mengarah ke kanan dan dinamakan sumbu kutub, sedangkan titik pangkalnya disebut titik asal atau kutub (Suarsana, 2014).

Gambar 2. 4. Koordinat Kutub

Sumber: Sursana, 2014

Suatu titik dinyatakan dengan pasangan (𝑟, 𝜃) dengan 𝑟 menyatakan jarak titik 𝑃 ke titik 𝑂 sedangkan 𝜃 adalah sudut antara sinar yang memancar dari titik 𝑂 melewati titik 𝑃 dengan sumbu 𝑥 positif, seperti pada Gambar 2.4.

𝑃(𝑟, 𝜃) 𝑟

𝜃

Koordinat kutub dapat membantu untuk memudahkan dalam mengubah persamaan kutub menjadi persamaan kartesius atau sebaliknya, sehingga titik 𝑃(𝑥, 𝑦) dalam sistem koordinat kartesius yang dinyatakan sebagai 𝑃(𝑟, 𝜃) dalam sistem koordinat kutub, seperti pada gambar di bawah ini:

Gambar 2. 5 Koordinat Kartesius

Sumber: Suarsana, 2014

Berdasarkan pada Gambar 2.5, Jika ∆ 𝑂𝑇𝑃 siku-siku di 𝑇, maka diperoleh hubungan sebagai berikut:

𝑥 = 𝑟 cos 𝜃 𝑦 = 𝑟 sin 𝜃 𝑟2 = 𝑥2 + 𝑦2 tan 𝜃 =𝑦 𝑥⟺ 𝜃 = 𝑎𝑟𝑐 tan 𝑦 𝑥 Contoh 2.2:

Nyatakan koordinat kartesius berikut ke dalam koordinat kutub: a. Titik 𝐵(3,3√3) b. Titik 𝐷(−√3, 1) Penyelesaian: a. i. menentukan jari-jari: 𝑦 𝑥 𝑂 𝑟 𝜃 𝑥 𝑦 𝑃(𝑥, 𝑦) 𝑇(𝑥, 0)

𝑟 = √𝑥2 _{+ 𝑦}2 _{= √3}2_{+ (3√3)}2 _{= √9 + 27 = √36 = 6} ii. menetukan sudut:

𝜃 = 𝑎𝑟𝑐 tan𝑦

𝑥= 𝑎𝑟𝑐 tan 3√3

3 = 60°

Karena nilai 𝑥 dan 𝑦 positif, sehingga titik 𝐵 ada di kuadran I dengan sudut 60°.

Jadi, koordinat kutub dari 𝐵(3,3√3) adalah 𝐵(6,60°). b. i. menentukan jari-jari:

𝑟 = √𝑥2_{+ 𝑦}2 _{= √(−√3)}2_{+ 1}2 _{= √3 + 1 = √4 = 2} ii. menetukan sudut:

𝜃 = 𝑎𝑟𝑐 tan𝑦

𝑥= 𝑎𝑟𝑐 tan 1

−√3= 30°

Karena nilai 𝑥 negatif dan 𝑦 positif, akibatnya titik 𝐷 ada di kuadran II, sehingga sudutnya: 180° − 30° = 150°.

Jadi, koordinat kutub dari 𝐷(−√3, 1) adalah 𝐷(2,150°).

C. Lingkaran

Definisi 2.1 (Muharti, 1973: 82)

Lingkaran adalah semua himpunan titik-titik yang berjarak sama dengan suatu titik tertentu yang disebut titik pusat. Jarak titik-titik dengan titik tertentu disebut jari-jari.

Berikut ini akan ditunjukkan persamaan lingkaran yang bertitik pusat di titik asal (0,0) dan persamaan lingkaran yang bertitik pusat di titik (𝑎, 𝑏).

Gambar 2. 6 Lingkaran Berpusat di (0,0)

Sumber: Suarsana, 2014

Pada Gambar 2.6 nampak lingkaran dengan titik pusat di 𝑂(0,0) dan jari-jari 𝑟 satuan panjang. Untuk menemukan persamaan lingkaran, misalkan diberikan titik 𝐴(𝑥, 𝑦). Jarak titik 𝑂 ke titik 𝐴 dengan teorema Phytagoras adalah √𝑥2_{+ 𝑦}2 _{. Namun diketahui bahwa 𝑂𝑇̅̅̅̅ adalah} jari-jari lingkaran, maka diperoleh persamaan lingkaran yang berpusat di titik (0,0):

√𝑥2 _{+ 𝑦}2 _{= 𝑟}

𝑥2_{+ 𝑦}2 _{= 𝑟}2 _(2.1) Selanjutnya untuk persamaan lingkaran yang berpusat di titik (𝑎, 𝑏) dengan jari-jari 𝑟 dapat diturunkan sebagai berikut:

𝑂

Gambar 2. 7 Lingkaran yang Berpusat di Titik A(𝑎, 𝑏)

Sumber: http://memedwachiantosmkn10.blogspot.com diakses pada 10 Desember 2018.

Menentukan persamaan lingkaran seperti Gambar 2.7, ambil sembarang titik pada lingkaran, misal titik 𝑃(𝑥, 𝑦). Pada segitiga siku-siku 𝐴𝑃′𝑃 didapat jarak titik 𝐴 ke titik 𝑃 adalah √(𝑥 − 𝑎)2_{+ (𝑦 − 𝑏)}2_. Padahal jaraknya adalah jari-jari lingkaran, yaitu 𝑟, maka diperoleh persamaan di bawah ini:

√(𝑥 − 𝑎)2_{+ (𝑦 − 𝑏)}2 _{= 𝑟}

(𝑥 − 𝑎)2_{+ (𝑦 − 𝑏)}2 _{= 𝑟}2 _(2.2) Karena 𝑃(𝑥, 𝑦) adalah sembarang titik pada lingkaran tersebut, berlaku persamaan di atas untuk setiap titik pada lingkaran tersebut. Sehingga persamaan lingkaran yang berpusat 𝐴(𝑎, 𝑏) dengan berjari-jari satuan adalah:

(𝑥 − 𝑎)2_{+ (𝑦 − 𝑏)}2 _{= 𝑟}2 _(2.3) 𝑥2_{+ 𝑦}2_{+ 𝐴𝑥 + 𝐵𝑦 + 𝐶 = 0 disebut sebagai persamaan umum} lingkaran. Apabila diketahui persamaan umum suatu lingkaran, maka

(𝑥 − 𝑎)

𝑃′_{(𝑥, 𝑏)}

dapat ditemukan koordinat-koordinat titik pusat dan jari-jarinya. Persamaan bentuk umum tersebut diubah menjadi:

𝑥2_{+ 𝐴𝑥 +}1 4𝐴 2 _{+ 𝑦}2_{+ 𝐵𝑦 +}1 4𝐵 2 ₌1 4𝐴 2₊1 4𝐵 2_{− 𝐶} (𝑥 +1 2𝐴) 2 + (𝑦 +1 2𝐵) 2 =1 4𝐴 2 ₊1 4𝐵 2_{− 𝐶 (2.4)} Dari persamaan (2.3) dan (2.4), dapat disimpulkan bahwa titik pusat lingkaran adalah (−1

2𝐴, − 1

2𝐵) dan jari-jarinya adalah:

𝑟 = √1 4𝐴

2₊1 4𝐵

2_{− 𝐶.}

Dari pernyataan di atas terkait titik pusat dan jari lingkaran, terdapat 2 kemungkinan yang dapat terjadi, yaitu:

a. Jika 1 4𝐴

2₊1 4𝐵

2_{− 𝐶 > 0, persamaan bentuk umum itu} menyatakan lingkaran nyata.

b. Jika 1 4𝐴

2 ₊1 4𝐵

2_{− 𝐶 = 0, persamaan bentuk umum itu} menyatakan lingkaran dengan jari-jari nol, berarti berupa sebuah titik.

c. Jika 1 4𝐴

2₊1 4𝐵

2_{− 𝐶 < 0, persamaan bentuk umum itu} menyatakan lingkaran imajiner, yaitu lingkaran yang tidak mudah untuk dibayangkan.

2. Lingkaran Satuan

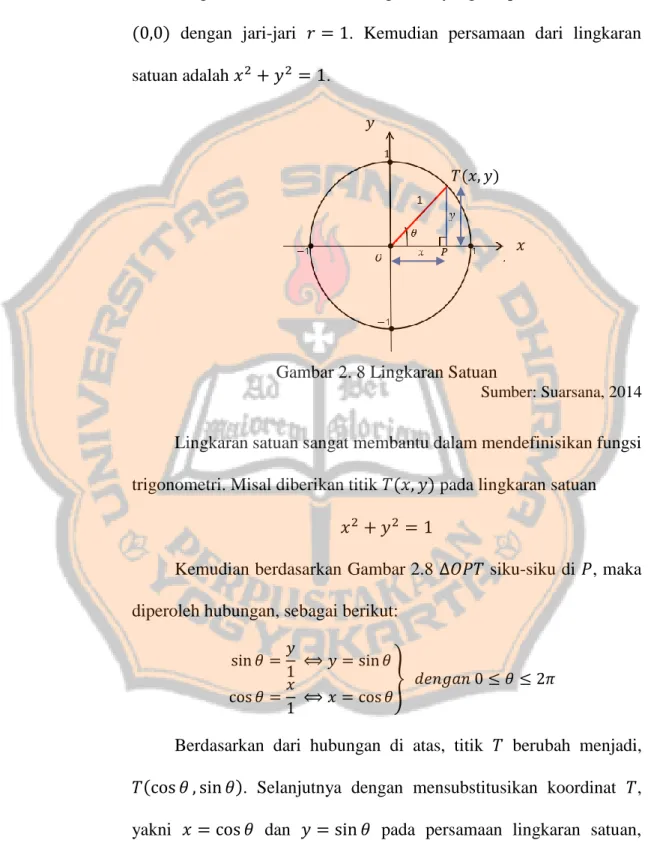
Lingkaran satuan adalah lingkaran yang berpusat di titik asal (0,0) dengan jari-jari 𝑟 = 1. Kemudian persamaan dari lingkaran satuan adalah 𝑥2 + 𝑦2 = 1.

Gambar 2. 8 Lingkaran Satuan

Sumber: Suarsana, 2014

Lingkaran satuan sangat membantu dalam mendefinisikan fungsi trigonometri. Misal diberikan titik 𝑇(𝑥, 𝑦) pada lingkaran satuan

𝑥2 _{+ 𝑦}2 _{= 1}

Kemudian berdasarkan Gambar 2.8 ∆𝑂𝑃𝑇 siku-siku di 𝑃, maka diperoleh hubungan, sebagai berikut:

sin 𝜃 =𝑦

1 ⟺ 𝑦 = sin 𝜃 cos 𝜃 =𝑥

1 ⟺ 𝑥 = cos 𝜃

} 𝑑𝑒𝑛𝑔𝑎𝑛 0 ≤ 𝜃 ≤ 2𝜋

Berdasarkan dari hubungan di atas, titik 𝑇 berubah menjadi, 𝑇(cos 𝜃 , sin 𝜃). Selanjutnya dengan mensubstitusikan koordinat 𝑇, yakni 𝑥 = cos 𝜃 dan 𝑦 = sin 𝜃 pada persamaan lingkaran satuan, sehingga persamaan lingkaran satuan menjadi:

1

𝑇(𝑥, 𝑦) 𝑦

cos2𝜃 + sin2𝜃 = 1. (2.5)

D. Segi-𝒏

Definisi 2.2 (Bronshtein, 1998: 175)

Segi-𝑛 adalah bidang datar yang dibatasi oleh garis lurus sebanyak n

garis/sisi pada bidang datar, kemudian jumlah besar sudut dalamnya adalah

(𝑛 − 2) 180°. Segi-𝑛 disebut beraturan jika sisi-sisi dan sudut-sudutnya

adalah sama panjang dan sama besar. Sedangkan segi-𝑛 disebut tak

beraturan ketika sisi-sisinya tidak sama panjang dan besar sudut-sudut dalamnya berbeda.

Contoh seperti pada Gambar 2.9, 2.10 dan 2.11, berturut-turut persegi adalah segiempat beraturan, segitiga sama sisi adalah segitiga beraturan, dan segilima tak beraturan.

Gambar 2. 10 Segitiga Sama Sisi Gambar 2. 9 Persegi

Segi-𝑛 dikatakan sebagai segi-𝑛 yang dibuat di dalam lingkaran satuan apabila segi-𝑛 dibuat melalui titik-titik sudut yang berada pada lingkaran satuan dan daerah yang dibatasi oleh segi-𝑛 berada di dalam lingkaran satuan. Jika segi-𝑛 dalam lingkaran merupakan segi-𝑛 beraturan, maka titik pusat lingkaran juga merupakan titik pusat dari segi-𝑛, seperti pada Gambar 2.12 di bawah ini. Titik 𝑂 merupakan titik pusat dari segi-6 sekaligus lingkaran satuan serta 𝑂𝐹̅̅̅̅ adalah 𝑟 atau jari-jari lingkaran satuan.

Gambar 2. 12 Segienam Dalam Lingkaran

Sumber: Bronshtein, 1998

Selanjutnya segi-𝑛 dikatakan sebagai segi-𝑛 yang dibuat di luar lingkaran satuan apabila sisi-sisi pada segi-𝑛 bersinggungan dengan lingkaran. Jika segi-𝑛 yang dibuat di luar lingkaran satuan merupakan segi-𝑛 beraturan, maka titik pusat lingkaran satuan juga merupakan titik pusat dari segi-𝑛, seperti pada Gambar 2.13 di bawah ini. Titik 𝑂 merupakan titik pusat segi-6 sekaligus lingkaran dan 𝑑(𝑂𝐺̅̅̅̅) = 𝑟 atau jari-jari lingkaran satuan.

Gambar 2. 13 Segienam Luar Lingkaran

Sumber: Bronshtein, 1998

E. Persamaan Garis Lurus

Garis lurus adalah garis yang menghubungkan dua titik dengan jarak terdekat. Sehingga persamaan garis lurus adalah suatu persamaan yang menyatakan titik-titik yang dilalui oleh suatu garis lurus. Persamaan garis lurus ada beberapa macam jenisnya, menurut Suarsana (2014) yakni:

1. Garis Sejajar Sumbu-Sumbu Koordinat

Gambar 2. 14 Garis 𝑙 ∥ Sumbu 𝑦

Sumber: Suarsana, 2014 𝐹 𝐴 _{𝐺 𝐵} 𝐶 𝐷 𝐸 𝑂 𝑟 𝑦 𝑥 𝑂 𝑙 𝐴(𝑎, 0)

Gambar 2. 15 Garis 𝑠 ∥ Sumbu 𝑥

Sumber: Suarsana, 2014

Garis 𝑙 pada Gambar 2.14 melalui titik 𝐴(𝑎, 0) dan sejajar sumbu-𝑦 yang berarti semua ruas garis yang dibuat melalui sumbu-sumbu-𝑦 dan tegak lurus dengan garis 𝑙 sama panjang yakni berjarak sebesar 𝑎, sehingga persamaan garis 𝑙 dinyatakan sebagai 𝑥 = 𝑎. Selanjutnya garis 𝑠 pada Gambar 2.15 melalui titik 𝐵(0, 𝑏) dan sejajar sumbu-𝑥, sehingga persamaan garis 𝑠 merupakan 𝑦 = 𝑏.

2. Garis Melalui Titik Asal dan Sebuah Titik Tertentu

Persamaan garis lurus yang melalui titik asal (0,0) dan sebuah titik tertentu 𝑃(𝑥₁, 𝑦₁), dapat dibuat dengan sebelumnya menentukan atau mencari sifat-sifat yang sama yang dimiliki oleh semua titik pada garis, misal garis 𝑙, seperti gambar di bawah ini:

Gambar 2. 16 Garis 𝑙 yang Melewati Titik Asal Dan Sebuah Titik Tertentu Sumber: Suarsana, 2014 𝑦 𝑥 𝑂 𝑠 𝐵(0, 𝑏) 𝑦 𝑥 𝑂 𝑙 𝑃(𝑥1, 𝑦1) 𝑇(𝑥2, 𝑦2) 𝑄(𝑥1, 0) 𝑅(𝑥2, 0) 𝛼 𝑆(0, 𝑦1) 𝑈(0, 𝑦2)

Ambilah sebarang titik T dan titik P pada garis 𝑙 dan titik R dan Q masing-masing adalah proyeksi titik T dan P pada sumbu-𝑥. Misalkan 𝑇(𝑥₂, 𝑦₂) dan 𝑅(𝑥2, 0), 𝑃(𝑥1, 𝑦1) dan 𝑄(𝑥1, 0) serta 𝑇𝑅 ∥ 𝑃𝑄 maka:

𝑑(𝑇𝑅̅̅̅̅): 𝑑(𝑂𝑅̅̅̅̅) = 𝑑(𝑃𝑄̅̅̅̅): 𝑑(𝑂𝑄̅̅̅̅) 𝑦2: 𝑥2 = 𝑦1: 𝑥1 atau dapat ditulis

𝑦₂ 𝑥2

= 𝑦1 𝑥1

Jika 𝛼 adalah sudut yang dibentuk garis 𝑙 dengan sumbu 𝑥 arah positif, maka:

𝑦₂ 𝑥₂ =

𝑦₁

𝑥₁ = tan 𝜃

Dapat dilihat bahwa perbandingan ordinat dan absis setiap titik garis 𝑙 adalah tan 𝜃. Apabila sebarang titik (𝑥, 𝑦) terletak pada garis 𝑙, maka diperoleh:

𝑦

𝑥 = tan 𝜃

Mengingat titik 𝑃(𝑥1, 𝑦1) diketahui, maka nilai tan 𝜃, sehingga diperoleh: 𝑦 𝑥= tan 𝜃 𝑦 𝑥= 𝑦1 𝑥₁

Jadi persamaan garis lurus 𝑙 yang melalui titik asal 𝑂 dan 𝑃(𝑥₁, 𝑦₁) adalah:

𝑦 =𝑦1 𝑥1

𝑥 (2.6)

3. Garis Melalui Dua Titik yang Diketahui

Garis yang melalui dua titik yaitu suatu garis lurus yang dibuat melalui dua buah titik yang diberikan misalkan titik 𝐴(𝑥₁, 𝑦₁) dan titik 𝐵(𝑥₂, 𝑦₂) dapat merupakan titik yang berbeda atau pun dua titik yang saling berhimpit. Persamaan garis yang melalui dua titik yang diketahui dapat dinyatakan sebagai berikut:

Gambar 2. 17 Garis 𝑙 yang Melewati Dua Titik

Sumber: Suarsana, 2014

Pada Gambar 2.17, garis lurus 𝑙 melalui titik-titik 𝐴(𝑥₁, 𝑦₁) dan 𝐵(𝑥₂, 𝑦₂) yang diketahui, dengan bantuan teorema Phytagoras dan jarak dua titik, dapat dinyatakan:

tan𝜃=𝑑(𝐶𝐵̅̅̅̅) 𝑑(𝐴𝐶̅̅̅̅)=

𝑦2− 𝑦1 𝑥2− 𝑥1

Langkah untuk menentukan persamaan garis yang melalui dua titik yang diketahui, diawali dengan mengambil sebarang titik 𝑃(𝑥, 𝑦)

𝑦 𝑥 𝑂 𝑙 𝐵(𝑥2, 𝑦2) 𝐴(𝑥1, 𝑦1) 𝐶(𝑥2, 𝑦1) 𝑃(𝑥, 𝑦) 𝜃 𝛼 (𝑥2, 0) (𝑥, 0) (𝑥1, 0) (0, 𝑦1) (0, 𝑦) (0, 𝑦2)

pada garis lurus 𝑙, maka gradien garis lurus 𝑙 sama juga dengan gradien ruas garis 𝐴𝐵̅̅̅̅.

tan𝜃 =𝑦 − 𝑦1 𝑥 − 𝑥1

Karena gradien ruas garis 𝐴𝑃̅̅̅̅ sama dengan gradien ruas garis 𝐴𝐵̅̅̅̅ sehingga diperoleh persamaan:

𝑦 − 𝑦1 𝑥 − 𝑥1

=𝑦2− 𝑦1 𝑥2− 𝑥1

(2.7)

atau dapat ditulis

𝑦 − 𝑦1 𝑦₂− 𝑦₁ =

𝑥 − 𝑥1

𝑥₂− 𝑥₁ (2.8) Karena 𝑃(𝑥, 𝑦) adalah sebarang titik pada garis lurus 𝑙, maka persamaan (2.8) merupakan persamaan garis lurus yang melalui titik 𝐴(𝑥₁, 𝑦₁) dan 𝐵(𝑥₂, 𝑦₂).

4. Garis Melalui Suatu Titik Tertentu dengan Gradien yang Diketahui Persamaan garis juga dapat dibuat apabila diberikan satu titik dan gradien garis tersebut juga diketahui. Misalkan sebuah garis 𝑔 dibuat melalui titik 𝐴(𝑥₁, 𝑦₁) dan gradien garis 𝑔 yaitu 𝑚. Selanjutnya diambil sebarang titik 𝑃(𝑥, 𝑦) pada garis 𝑔, sehingga gradien ruas garis 𝐴𝑃̅̅̅̅ adalah

𝑦 − 𝑦₁ 𝑥 − 𝑥1

Gambar 2.18 Garis 𝑔 yang Melewati Suatu Titik dan Gradien Garis 𝑔 Diketahui

Sumber: Suarsana, 2014

Gradien ruas garis 𝐴𝑃̅̅̅̅ sama saja dengan gradien garis 𝑔, karena gradien garis 𝑔 adalah 𝑚, maka diperoleh persamaan sebagai berikut:

𝑦 − 𝑦₁ 𝑥 − 𝑥₁ = 𝑚

𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁) (2.9) Karena 𝑃(𝑥, 𝑦) adalah sebarang titik pada garis lurus 𝑔, persamaan garis lurus yang melalui titik (𝑥₁, 𝑦₁) dengan gradien 𝑚 adalah:

𝑦 − 𝑦₁ = 𝑚(𝑥 − 𝑥₁) (2.10) 5. Garis dengan Perpotongan Kedua Sumbu Diketahui

Suatu garis lurus dapat dibuat berpotongan dengan sumbu-𝑋 dan sumbu-𝑌 masing-masing berpotongan di titik 𝐴(0, 𝑎) dan 𝐵(𝑏, 0), atau juga dapat dikatakan persamaan garis yang melalui dua titik yang masing-masing berada di sumbu-𝑥 dan sumbu-𝑦.

𝑦 𝑥 𝑂 𝑔 𝑃(𝑥, 𝑦) 𝐴(𝑥1, 𝑦1) 𝑄(𝑥, 𝑦1)

Gambar 2. 19 Garis 𝑔 yang Berpotongan dengan Kedua Sumbu

Sumber: Suarsana, 2014

Berdasarkan Gambar 2.19 diberikan suatu garis yang melalui dua titik yaitu 𝐴(0, 𝑎) dan 𝐵(𝑏, 0), sehingga menurut persamaan (2.8) persamaan garisnya adalah:

𝑦 − 𝑦₁ 𝑦2− 𝑦1

= 𝑥 − 𝑥1 𝑥2− 𝑥1

Selanjutnya dengan mensubtitusikan 𝐴(0, 𝑎) dan 𝐵(𝑏, 0) ke persamaan (2.8), didapat: 𝑦 − 0 𝑏 − 0= 𝑥 − 𝑎 0 − 𝑎 𝑦 𝑏= 𝑥 − 𝑎 −𝑎 𝑦 𝑏= 𝑥 −𝑎+ 1 𝑦 𝑏+ 𝑥 𝑎= +1 𝑎𝑦 + 𝑏𝑥 = 𝑎𝑏 Akhirnya didapat persamaan garis yang melalui titik 𝐴(𝑎, 0) dan 𝐵(0, 𝑏) adalah 𝑎𝑦 + 𝑏𝑥 = 𝑎𝑏 (2.11) 𝑦 𝑥 𝑂 𝑔 𝐴(𝑎, 0) 𝐵(0, 𝑏)

F. Konversi Sudut Radian Dalam Derajat

Definisi 2.3 (Zen, 2012: 39)

Sudut adalah dua sinar garis yang bertemu di satu titik yang disebut titik sudut. Ukuran sudut yang sering digunkaan adalah “derajat” yang dinotasikan °.

Satu derajat dapat dituliskan: 1° = 1

360𝑝𝑢𝑡𝑎𝑟𝑎𝑛

Ukuran sudut yang lazim digunakan selain “derajat” adalah “radian” (disingkat: rad), satu radian didefinisikan sebagai ukuran sudut di dalam sebuah lingkaran yang diapit oleh dua jari-jari dan panjang busur lingkaran yang sama dengan panjang jari-jari tersebut. Satu radian dapat dituliskan:

1 𝑟𝑎𝑑 =180°

𝜋 𝑎𝑡𝑎𝑢 1° = 𝜋 180𝑟𝑎𝑑

Contoh 2.3:

Ubahlah ukuran sudut berikut ke dalam ukuran radian! a. 30° b. 100° Penyelesaian: a. 30° = 30 × 𝜋 180𝑟𝑎𝑑 = 𝜋 6𝑟𝑎𝑑 b. 100° = 100 × 𝜋 180𝑟𝑎𝑑 = 5𝜋 9 𝑟𝑎𝑑

G. Turunan Parsial

Definis 2.4 (Purcell, 2007: 624)

Andaikan bahwa 𝑓 adalah suatu fungsi dua peubah 𝑥 dan 𝑦. Jika 𝑦

ditahan agar konstan, misalnya 𝑦 = 𝑦0, maka 𝑓(𝑥, 𝑦0) menjadi fungsi satu

peubah 𝑥. Turunannya di 𝑥 = 𝑥₀ di sebut turunan parsial terhadapa 𝑥 di (𝑥0, 𝑦0) dan 𝑓𝑥(𝑥0, 𝑦0). Jadi, 𝑓_𝑥(𝑥₀, 𝑦₀) = lim ∆𝑥→0 𝑓(𝑥₀+ ∆𝑥, 𝑦₀) − 𝑓(𝑥₀, 𝑦₀) ∆𝑥 (2.12) Demikian pula, turunan parsial 𝑓 terhadapat 𝑦 dinyatakan oleh 𝑓_𝑦(𝑥0, 𝑦0), dan dituliskan sebagai,

𝑓_𝑦(𝑥0, 𝑦0) = lim_∆𝑥→0

𝑓(𝑥0, 𝑦0+ ∆𝑦) − 𝑓(𝑥0, 𝑦0) ∆𝑦

Misal diberikan 𝑧 = 𝑓(𝑥, 𝑦), terdapat cara penelitian lainnya dengan menggunakan notasi 𝜕 yang merupakan lambang khas dalam matematika dan disebut tanda turunan parsial.

𝑓𝑥(𝑥, 𝑦) = 𝜕𝑧 𝜕𝑥= 𝜕𝑓(𝑥, 𝑦) 𝜕𝑥 𝑓𝑦(𝑥, 𝑦) = 𝜕𝑧 𝜕𝑦= 𝜕𝑓(𝑥, 𝑦) 𝜕𝑦 Contoh 2.4:

Jika 𝑧 = 𝑥2sin(𝑥𝑦2), carilah 𝜕𝑧 𝜕𝑥 dan

𝜕𝑧 𝜕𝑦!

Penyelesaian: 𝜕𝑧 𝜕𝑥= 𝑥 2𝜕 sin(𝑥𝑦 2₎ 𝜕𝑥 + sin(𝑥𝑦 2₎𝜕𝑥 2 𝜕𝑥 𝜕𝑧 𝜕𝑥= 𝑥 2𝜕 sin(𝑥𝑦 2₎ 𝜕𝑥 + sin(𝑥𝑦 2₎𝜕𝑥 2 𝜕𝑥 = 𝑥2cos(𝑥𝑦2)𝜕(𝑥𝑦 2₎ 𝜕𝑥 + sin(𝑥𝑦 2_{) ⋅ 2𝑥} = 𝑥2_cos(𝑥𝑦2_{) 𝑦}2_{+ 2𝑥 sin(𝑥𝑦}2₎ = 𝑥2𝑦2cos(𝑥𝑦2) + 2𝑥 sin(𝑥𝑦2₎ demikian pula, 𝜕𝑧 𝜕𝑦 = 𝑥 2𝜕 sin(𝑥𝑦2) 𝜕𝑦 + sin(𝑥𝑦 2₎𝜕𝑥2 𝜕𝑦 = 𝑥2_cos(𝑥𝑦2_{) ⋅ 2𝑥𝑦 + 0 = 2𝑥}3_{𝑦 cos(𝑥𝑦}2_). H. Diferensial Definisi 2.5 (Purcell, 2007: 143)

Misalkan 𝑦 = 𝑓(𝑥) adalah fungsi terdiferensial dari variabel bebas 𝑥. ∆𝑥 adalah pertambahan sebarang dalam variabel bebas 𝑥, sedangkan notasi 𝑑𝑥 disebut diferensial variabel bebas 𝑥, adalah sama dengan ∆𝑥. Selanjutnya

𝑓′(𝑥₀) = lim ∆𝑥0→0

𝑓(𝑥₀+ ∆𝑥) − 𝑓(𝑥₀) ∆𝑥

jika ∆𝑥 kecil, maka:

𝑓(𝑥₀ + ∆𝑥) − 𝑓(𝑥₀) ≈ ∆𝑥𝑓′_(𝑥

Ruas kiri ekpresi diatas adalah ∆𝑦 yang merupakan perubahan sebenarnya dalam variabel 𝑦 ketika 𝑥 berubah dari 𝑥 menjadi:

𝑥 + ∆𝑥 yakni

∆𝑦 = 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥). Notasi 𝑑𝑦, didefinisikan oleh 𝑑𝑦 = 𝑓′(𝑥)𝑑𝑥.

Contoh 2.4: Carilah 𝑑𝑦 jika: a. 𝑦 = 𝑥3_{− 3𝑥 + 1!} b. 𝑦 = sin(𝑥4_{− 3𝑥}2_{+ 11)!} Penyelesaian: a. 𝑑𝑦 = (3𝑥2 − 3)𝑑𝑥 b. 𝑑𝑦 = cos(𝑥4− 3𝑥2+ 11) ⋅ (4𝑥3− 6𝑥)𝑑𝑥 I. Integral Tentu Definisi 2.6 (Purcell, 2007: 224)

Misalkan suatu fungsi yang didefiniskan pada interval tertutup [𝑎, 𝑏].

Jika terdapat nilai

𝑙𝑖𝑚

‖𝑃‖→0∑(𝑓(𝑥̅𝑖)∆𝑥𝑖) 𝑛

𝑖=1

(2.14)

Maka dapat dikatakan 𝑓 terintegralkan pada [𝑎, 𝑏]. Lebih lanjut dinotasikan

∫ 𝑓(𝑥)𝑑𝑥 𝑏

disebut integral tentu dari fungsi 𝑓dari [𝑎, 𝑏], selanjutnya didefinisikan sebagai berikut: ∫ 𝑓(𝑥)𝑑𝑥 𝑏 𝑎 = lim ‖𝑃‖→0∑(𝑓(𝑥̅ )∆𝑥𝑖 𝑖) 𝑛 𝑖=1 (2.15) Pada ( ) b a f x dx



dapat disebut 𝑎 sebagai titik ujung bawah dan 𝑏 sebagai titik ujung atas untuk integral. Dalam definisi, ( )

b

a

f x dx



, secara implisit dapat diasumsikan bahwa 𝑎 < 𝑏. Sehingga juga dapat dinotasikan sebagai berikut dengan 𝑎 > 𝑏: ∫ 𝑓(𝑥) 𝑑𝑥 𝑏 𝑎 = − ∫ 𝑓(𝑥) 𝑑𝑥 𝑎 𝑏 , 𝑎 > 𝑏 (2.16)

J. Luas Daerah Suatu Kurva

Menurut Purcell (2007), terdapat dua masalah geometri yang memunculkan pemikiran terpenting dalam kalkulus. Masalah pencarian garis singgung berkaitan dengan turunan (derivative), dan permasalahan terkait mencari luas daerah berkaitan dengan integral tentu (definite integral).

1. Daerah di Atas Sumbu 𝑥

Suatu daerah dibatasi oleh sebuah kurva 𝑦 = 𝑓(𝑥) dan sumbu-𝑥 sepanjang 𝑎 sampai 𝑏 seperti Gambar 2.20.

Gambar 2. 20 Daerah di Atas Sumbu 𝑥

Sumber: Purcell, 2007

Misalkan 𝑦 = 𝑓(𝑥) menentukan persamaan kurva di bidang-𝑥𝑦 dan misalkan 𝑓 tak-negatif pada interval [𝑎, 𝑏], seperti ditunjukkan pada Gambar 2.20. Berdasarkan daerah 𝑅 yang dibatasi oleh grafik-grafik 𝑦 = 𝑓(𝑥), 𝑥 = 𝑎, 𝑥 = 𝑏 dan 𝑦 = 0. Terlihat bahwa 𝑅 adalah daerah tertutup yang dibatasi oleh 𝑦 = 𝑓(𝑥), diantara 𝑥 = 𝑎 dan 𝑥 = 𝑏. Luas 𝐴(𝑅), diberikan oleh:

𝐴(𝑅) = ∫ 𝑓(𝑥) 𝑏 𝑎

𝑑𝑥 (2.17) 2. Daerah di Bawah Sumbu 𝑥

Suatu daerah dibatasi oleh sebuah kurva 𝑦 = 𝑓(𝑥) dan sumbu-𝑥 sepanjang 𝑎 sampai 𝑏 seperti Gambar 2.21.

Gambar 2. 21 Daerah di Bawah Sumbu 𝑥

Sumber: Purcell, 2007 𝑦 𝑥 𝑏 𝑎 𝑓(𝑥) 𝑅 𝑦 𝑥 𝑏 𝑎 𝑓(𝑥) 𝑅

Luas adalah bilangan tak-negatif. Jika grafik 𝑦 = 𝑓(𝑥) terletak di bawah sumbu 𝑥 maka b ( )

a f x dx



adalah bilangan negatif, sehingga tidak dapat menyatakan suatu luas. Sehingga luasnya dinyatakan sebagai berikut:

𝐴(𝑅) = − ∫ 𝑓(𝑥) 𝑏 𝑎

𝑑𝑥 (2.18)

3. Daerah di Antara Dua Kurva

Gambar 2. 22 Daerah di Antara Dua Kurva

Sumber: Purcell, 2007

Berdasarkan pada Gambar 2.2 daerah yang dimaksud berada diantara kurva-kurva 𝑦 = 𝑓(𝑥) dan 𝑦 = 𝑔(𝑥) dengan 𝑔(𝑥) ≤ 𝑓(𝑥) pada [𝑎, 𝑏], seperti. Adapun untuk mencari luasanya menggunakan metode iris, aproksimasi, integrasi. Yakinkan untuk memperhatikan bahwa 𝑓(𝑥) − 𝑔(𝑥) memberikan tinggi yang benar dari irisan tipis tersebut.

K. Integral Kurva

Menurut Purcell (2007), integral garis atau integral kurva adalah

hasil dari generalisasi integral tentu ( ) b

a

f x dx

[𝑎, 𝑏] dengan suatu kurva 𝐶 di bidang-𝑥𝑦, sehingga menghasilkan integral yakni

 

,

C

f x y ds



.

Misalkan 𝐶 suatu kurva bidang mulus, 𝐶 diberikan soleh persamaan parameter

𝑥 = 𝑥(𝑡), 𝑦 = 𝑦(𝑡), [𝑎, 𝑏]

𝑥′ dan 𝑦′ kontinu dan tidak secara serentak nol pada [𝑎, 𝑏], andaikan bahwa 𝐶 terorientasi positif (arah positifnya berpadanan terhadap pertambahan nilai 𝑡) bahwa 𝐶 hanya ditelusuri sekali saat 𝑡 berubah dari 𝑎 ke 𝑏. Jadi, 𝐶 memiliki titik awal di (𝑥(𝑎), 𝑦(𝑎)) dan titik terakhir (𝑥(𝑏), 𝑦(𝑏)). Partisi dari selang [𝑎, 𝑏] menghasilkan pembagian kurva 𝐶 menjadi 𝑛 subbusur 𝑃𝑖−1𝑃𝑖

𝑎 = 𝑡₀ < 𝑡₁ < 𝑡₂ < ⋯ < 𝑡_𝑛 = 𝑏

Gambar 2. 23 Partisi C dari [𝑎, 𝑏]

Sumber: Purcell, 2007

Partisi dari [𝑎, 𝑏] ini menghasilkan suatu pembagian kurva 𝐶 ke dalam 𝑛 busur-bagian. Misalkan ∆𝑠𝑖 melambangkan panjang busur 𝑃𝑖−1𝑃𝑖 dan

misalkan |𝑃| merupakan aturan untuk mempartisi P; yaitu misalkan |𝑃| adalah ∆𝑡_𝑖 𝑡𝑒𝑟𝑏𝑒𝑠𝑎𝑟 = 𝑡_𝑖 − 𝑡_𝑖−1.

Contoh 2.5:

Pilih titik 𝑄𝑖(𝑥̅𝑖, 𝑦̅𝑖) pada subbusur 𝑃𝑖−1𝑃𝑖 seperti pada Gambar 2.23.

Gambar 2. 24 Luas Tirai Tegak Melengkung Sepanjang C

Selanjutnya memperhatikan jumlahan Riemann 1 ( , ) n i _{i i} i f x y s  



. Jika 𝑓

positif, jumlahan ini mengaproksimasi luas tirai tegak melengkung seperti Gambar 2.22. Jika 𝑓 kontinu pada daerah D yang mengandung kurva 𝐶. Maka jumlahan Riemann memiliki limit untuk |𝑃| → 0. Limit ini disebut integral garis dari 𝑓 sepanjang 𝐶 dari A ke B; yaitu

∫ 𝑓(𝑥, 𝑦)𝑑𝑠 𝐶 = lim |𝑃|→0∑ (𝑓(𝑥̅𝑖, 𝑦̅𝑖)∆𝑠𝑖) 𝑛 𝑖=1

Guna memperoleh perhitungan yang baik disajikan dalam parameter 𝑡 dan menjadi integral tentu biasa. Integral garis atas kurva 𝐶 dapat dinyatakan

𝑃𝑛= 𝐵 𝑧 = 𝑓(𝑥, 𝑦)

dalam integral tentu biasa dari 𝑎 sampai 𝑏 dalam parameter 𝑡, seperti di bawah ini: ∫ 𝑓(𝑥, 𝑦)𝑑𝑠 𝐶 = ∫ (𝑓(𝑥(𝑡), 𝑦(𝑡))√[𝑥′_(𝑡)]2_{+ [𝑦}′_(𝑡)]2_{) 𝑑𝑡} 𝑏 𝑎 (2.19) Contoh 2.6:

Hitung integral garis



3



C

x y ds



; dengan 𝐶 adalah kurva 𝑥 = 3𝑡, 𝑦 = 𝑡3_{, 0 ≤ 𝑡 ≤ 1!} Jawab: Diketahui: 𝑥 = 3𝑡 maka 𝑥′_{= 3 dan} 𝑦 = 𝑡3 _{maka 𝑦}′ _{= 3𝑡}2 𝑓(𝑥, 𝑦) = 𝑥3_{+ 𝑦}

Subtitusi nilai 𝑥 dan 𝑦 ke 𝑓(𝑥, 𝑦), sehingga menjadi fungsi dalam 𝑡, yakni, 𝑓(𝑡) = (3𝑡)3+ 𝑡3 = 27𝑡3 + 𝑡3 = 28𝑡3. Maka ∫ 𝑓(𝑥, 𝑦)𝑑𝑠 𝐶 = ∫ (𝑓(𝑥(𝑡), 𝑦(𝑡))√[𝑥′_(𝑡)]2_{+ [𝑦}′_(𝑡)]2_{) 𝑑𝑡} 𝑏 𝑎

Kemudian telah diberikan batas nilai t dari 0 hingga 1, selanjutnya batas tersebut sebagai nilai-nilai integral tentu, seperti di bawah ini,

∫ (𝑥3 + 𝑦)𝑑𝑠 𝐶 = ∫ (28𝑡3√[3]2_{+ [3𝑡}2_]2_{) 𝑑𝑡} 1 0 = ∫ (28𝑡3_{√9 + 9𝑡}4_{) 𝑑𝑡} 1 0

= 84 ∫ (𝑡3√1 + 𝑡4_{) 𝑑𝑡} 1 0 = 84 4 ∙ 2 3(1 + 𝑡 4₎3_2|𝑡 = 1 𝑡 = 0= 14(2√2 − 1) = 14(√2 − 1).

38

BAB III

AKIBAT TEOREMA GREEN PADA BIDANG

Bab III ini peneliti mempelajari akibat teorema Green pada bidang untuk mencari luas segi-𝑛. Perlu disadari bahwa akibat dari Teorema Green pada bidang dapat membantu dalam menyelesaikan persoalan integral garis dengan lebih efisien. Seperti beberapa contoh kasus yang akan ditunjukkan pada bab ini.

A. Teorema Green Pada Bidang

Teorema Green merupakan teorema yang cukup penting karena teori ini menyatakan hubungan antara integral garis yang dilakukan sepanjang kurva tetutup 𝐶 pada bidang dengan integral lipat dua (double integral) atas suatu daerah yang dibatasi oleh 𝐶. Teorema ini, dengan kata lain, menjelaskan bahwa permasalahan integral garis dalam menghitung luas daerah yang dibatasi suatu kurva dapat diselesaikan dengan akibat teorema Green dengan lebih baik/ efisien. Suatu kurva tertutup sederhana 𝐶 memiliki dua arah yaitu berlawanan arah dengan arah putarjarum jam/ CCW (counter-clock-wise) sebagai arah positif, dan searah dengan putaran jarum jam/ CW (clock-wise) sebagai arah negatif.

Jika 𝑅 ada suatu daerah tertutup dalam bidang 𝑋𝑌 yang dibatasi oleh kurva tertutup sederhana 𝐶. Misal 𝑀(𝑥, 𝑦) dan 𝑁(𝑥, 𝑦) masing fungsi kontinu dan mempunyai turunan parsial pertama yang juga kontinu dalam R, maka

∮ 𝑀 𝑑𝑥 + 𝑁 𝑑𝑦 𝐶 = ∬ (𝜕𝑁 𝜕𝑥 − 𝜕𝑀 𝜕𝑦) 𝑅 𝑑𝑥𝑑𝑦 (3.1)

Kurva tertutup 𝐶 dilintasi dalam arah positif (berlawanan arah jarum jam/ counter clockwise). Pembuktian teorema ini dapat dilihat pada Marsden (1976: 405-407).

B. Kasus-kasus Pengaplikasian Teorema Green dalam Bidang

Bagian ini menunjukkan bahwa akibat teorema Green pada bidang untuk mengitung luas dapat dilakukan dengan baik, untuk ke dalam beberapa permasalahan atau kasus. Berikut adalah kasus-kasus pengaplikasian Teorema Green dalam Bidang.

1. Kasus I

Teorema Green dalam bidang jika 𝐶 adalah sebuah kurva tertutup yang memiliki sifat bahwa sembarang garis lurus yang sejajar sumbu-sumbu koordinat memotong 𝑅 paling banyak pada dua buah titik.

Gambar 3. 1 Ilustrasi Kasus I (Elips)

𝑅 𝐹 𝐵 𝐴 𝐸 𝑏 𝑎 𝑒 𝑓 𝑦 𝑥 𝑦 = 𝑦1(𝑥) 𝑦 = 𝑦2(𝑥)

Bukti:

Misalkan persamaan kurva-kurva 𝐴𝐸𝐵 dan 𝐴𝐹𝐵 masing-masing adalah 𝑦 = 𝑦₁(𝑥) dan 𝑦 = 𝑦2(𝑥) seperti pada Gambar 3.1. Jika 𝑅 adalah daerah yang dibatasi oleh 𝐶, maka:

∬𝜕𝑀 𝜕𝑦 𝑑𝑥𝑑𝑦 𝑅 = ∫ [ ∫ 𝜕𝑀 𝜕𝑦 𝑑𝑦 𝑦2(𝑥) 𝑦=𝑦1(𝑥) ] 𝑑𝑥 𝑏 𝑥=𝑎 = ∫ 𝑀(𝑥, 𝑦) | 𝑌2(𝑥) 𝑦 = 𝑌₁(𝑥) 𝑏 𝑥=𝑎 𝑑𝑥 = ∫ [𝑀(𝑥, 𝑌₂) − 𝑀(𝑥, 𝑌1)]𝑑𝑥 𝑏 𝑥=𝑎 = − ∫ 𝑀(𝑥, 𝑌₁)𝑑𝑥 𝑏 𝑎 − ∫ 𝑀(𝑥, 𝑌₂)𝑑𝑥 𝑏 𝑎 = ∮ 𝑀 𝑑𝑥 𝐶 Sehingga diperoleh ∮ 𝑀 𝑑𝑥 𝐶 = − ∬𝜕𝑀 𝜕𝑦 𝑑𝑥𝑑𝑦 𝑅 (1)

Berikutnya, dengan cara yang sama, misalkan persamaan-persamaan kurva-kurva 𝐸𝐴𝐹 dan 𝐸𝐵𝐹, masing-masing adalah 𝑥 = 𝑋₁(𝑦) dan 𝑥 = 𝑋2(𝑦), maka

∬𝜕𝑁 𝜕𝑥𝑑𝑥𝑑𝑦 𝑅 = ∫ [ ∫ 𝜕𝑁 𝜕𝑥𝑑𝑥 𝑥2(𝑦) 𝑥=𝑥1(𝑦) ] 𝑑𝑦 𝑓 𝑦=𝑒 = ∫ 𝑁(𝑥, 𝑦) |𝑋2(𝑦) 𝑥 = 𝑋₁(𝑦) 𝑓 𝑒 𝑑𝑦 = ∫[𝑁(𝑋₂, 𝑦) − 𝑁(𝑋₁, 𝑦)]𝑑𝑦 𝑓 𝑒 = ∫ 𝑁(𝑋₁, 𝑦) 𝑑𝑦 𝑓 𝑒 + ∫ 𝑁(𝑋₂, 𝑦) 𝑑𝑦 𝑓 𝑒 = ∮ 𝑁 𝑑𝑦 𝐶 Sehingga diperoleh: ∮ 𝑁 𝑑𝑦 𝐶 = ∬𝜕𝑁 𝜕𝑦𝑑𝑥𝑑𝑦 𝑅 (2)

Jumlahkan (1) dan (2) untuk memperoleh:

C R N M M dx N dy dxdy y y      _  _    





∎

2. Kasus II

Gambar 3. 2 Daerah yang Dibatasi Oleh 𝑦 = 𝑥 dan 𝑦 = 𝑥2 Akan dibuktikan akibat teorema Green pada bidang untuk



2



2

C

xyy dxx dy



, dengan 𝐶 adalah kurva tertutup dari daerah yang dibatasi oleh 𝑦 = 𝑥 dan 𝑦 = 𝑥2, yang berpotongan di titik (0,0) dan titik (1,1).

Bukti:

Sepanjang 𝑦 = 𝑥2 dari (0,0), sampai (1,1), integral garisnya yaitu, ∫ ((𝑥)(𝑥2) + 𝑥4_{)𝑑𝑥 + (𝑥}2_{)(2𝑥)𝑑𝑥} 1 0 = ∫ (3𝑥3+ 𝑥4)𝑑𝑥 1 0 = 19 20 Sedangkan sepanjang 𝑦 = 𝑥 dari (1,1), sampai (0,0) integral garisnya yaitu, ∫ ((𝑥)(𝑥) + 𝑥2)𝑑𝑥 + (𝑥2)𝑑𝑥 0 1 = ∫ 3𝑥2𝑑𝑥 0 1 = −1

Maka integral lintasannya adalah 19 1 1

20 20

3. Kasus III

Gambar 3. 3 Daerah D yang dibatasi oleh Kurva C

Sumber: https://id.wikipedia.org/wiki/Teorema_Green diakses pada 12 Desember 2018

Akibat teorema Green pada bidang juga dapat digunakan untuk menghitung luas suatu daerah dengan konsep integral garis. Jika suatu daerah 𝐷 pada bidang mempunyai batas 𝐶, dengan kurva 𝐶 sederhana, tertutup, mulus sepotong-sepotong, seperti Gambar 3.3 maka luas 𝐷 diberikan oleh: 𝐴(𝐷) =1 2∮ 𝑥 𝑑𝑦_𝐶 − 𝑦 𝑑𝑥 (3.2) Bukti: Diberikan ( , ) 2 y M x y   dan ( , ) 2 x

N x y   dan terapkan akibat teorema Green untuk menghitung luas.

∮ 𝑥 2 𝑑𝑦 𝐶 −𝑦 2 𝑑𝑥 = ∬ ( 𝜕 𝜕𝑥( 𝑥 2) − 𝜕 𝜕𝑦(− 𝑦 2)) 𝑑𝑥𝑑𝑦 𝐷

= ∬ (1 2+ 1 2) 𝑑𝐴 𝐷 = 𝐴(𝑅) ∎

45

BAB IV

PEMBAHASAN DAN HASIL

Bab ini membahas tentang penggunaan atau pengaplikasian Teorema Green untuk menghitung pendekatan luas lingkaran. Luas lingkaran akan didekati menggunakan luas dari lingkaran satuan yakni lingkaran yang berjari-jari 1, berpusat di titik pangkal (0,0), dan memiliki luas 𝜋. Metode yang digunakan dalam penelitian ini yaitu studi pustaka dengan membaca buku-buku yang berkaitan dengan luas daerah dan Teorema Green. Seperti yang telah diulas pada Bab III bahwa teorema ini dapat diaplikasikan untuk menghitung luas daerah, prinsipnya dalam Teorema Green mirip dengan integral garis yakni menghitung panjang lintasan suatu kurva. Sedangkan dalam bidang teorema green menghitung luasan suatu daerah yang dibatasi oleh suatu kurva, dan kurva tersebut masing-masing lintasannya terbentuk dari dua titik yang saling berdekatan. Penelitian ini mengambil pendekatan yang dibangun dari segi-𝑛 beraturan dan tidak beraturan yang dibuat di dalam serta di luar lingkaran satuan. Nilai 𝑛 yang akan digunakan adalah 4, 8, 16, 32, 64, 128, 256, 512, dan 1024.

Teorema Green yang ada tidak dapat langsung digunakan begitu saja untuk menghitung luas daerah segi-𝑛, melainkan perlu dikaji kembali secara analitik sehingga ditemukan formula yang dapat digunakan untuk menghitung luas segi-𝑛. Langkah ini membutuhkan pengetahuan tentang persamaan garis melalui dua titik, diferensial, integral garis, dan Teorema Green. Luas daerah dalam skripsi ini seperti yang telah dikatakan di atas, yakni menggunakan luas daerah segi-𝑛 beraturan dan tidak beraturan. Aplikasi Teorema Green pada bidang dapat digunakan untuk

menghitung luas daerah tersebut, karena kurva yang membatasi daerah tersebut memenuhi syarat agar teorema ini dapat digunakan. Adapun syarat-syaratnya yakni suatu daerah yang dibatasi oleh kurva tertutup yang sederhana, mulus sepotong-sepotong, dan tetap mempertahankan luasan berada disebelah kiri lintasan.

Penelitian ini membutuhkan titik sudut-titik sudut dari segi-𝑛. Kemudian titik-titik yang saling berdekatan disubstitusikan ke dalam persamaan yang telah didapat. Melalui proses tersebut akan diperoleh luasan sebelah kiri dari garis yang terbentuk melalui dua titik yang berdekatan dan arah integrasinya berlawanan arah jarum jam. Proses ini terus diulang dengan pasangan titik yang lain hingga pasangan titik (𝑛 − 1, 𝑛), setelah itu luasan pada masing-masing lintasan yang didapat kemudian dijumlahkan sehingga didapat luas daerah sepanjang lintasan 𝐶 dari segi-𝑛 beraturan di dalam dan di luar lingkaran satuan. Luas dari segiempat beraturan, segidelapan beraturan, dst, menjadi data yang akan diamati.

Pada penelitian ini peneliti harus menemukan rumus untuk menghitung segi-𝑛 di dalam ataupun diluar baik beraturan maupun tidak beraturan

A. Formulasi Luas Segi-𝒏 Menggunakan Akibat Teorema Green Pada

Bidang

Pada awal dari pembahasan ini telah dikatakan bahwa persamaan yang ada tidak dapat serta-merta digunakan untuk menghitung luas daerah yang dicari. Pembahasan diawali dengan mengkaji beberapa aturan yang akan digunkaan dalam menjelaskan penggunaan akibat Teorema Green pada bidang untuk menghitung luasan. Bagian ini merupakan tahapan mengkaji