MODEL SPASIAL SUDUT ZENITH MATAHARI PADA LAPISAN F IONOSFER

ISSN 0853 - 0823

MODEL SPASIAL SUDUT ZENITH MATAHARI PADA LAPISAN

F

₂

IONOSFER

Slamet Syamsudin

Pusat Pemanfaatan Sains Antariksa , LAPAN Jl. Dr. Junjunan No. 133, Bandung.

INTISARI

Persamaan cosinus zenith matahari di lapisan F₂ ionosfer diturunkan dari sistem persamaan differensial linier orde satu. Persamaan cosinus zenith matahari yang diperoleh terdiri dari tiga bagian yaitu pada waktu siang hari , waktu senja hari dan malam hari. Untuk menghindari diskontinuitas harga cosinus zenith tepat pada saat matahari terbit maka harga cosinus zenith matahari diwaktu siang diambil sebagai harga maksimal antara siang hari dan harga cosinus zenith matahari pada saat matahari terbenam ( Levin , 1978 ). Dalam melakukan perhitungan cosinus zenith dalam perioda 24 jam maka diperlukan persaamaan waktu yang membedakan antara siang dan malam, dimana persamaan waktu ini tergantung kepada lokasi yaitu lintang, bujur dan waktu yaitu tanggal dan bulan. Waktu yang digunakan dalam menghitung cosinus zenith ini pada setiap lokasi adalah waktu universal.

I. PENDAHULUAN

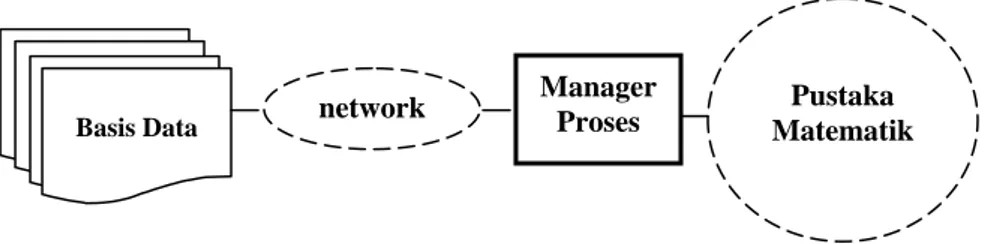
Model matematik sebagai mesin pengolah data untuk memberikan informasi frekuensi merupakan hasil inovasi para peneliti dan telah banyak dipublikasikan dalam bentuk journal , baik secara nasional maupun internasional. Model-model matematik tersebut di implementasikan sebagai salah satu piranti lunak pada sistem ini dalam bentuk pustaka standar dan hubungan pustaka ini dengan sistem informasi disajikan pada Gambar 1.

Gambar 1. Skema model perhitungan sudut zenith matahari

Manager proses adalah suatu modul yang langsung berhubungan dengan pustaka matematik sedangkan keterkaitan manager sistem dengan basis data adalah melalui network sistem. Pengguna tidak perlu mengetahui kinerja sistem secara internal oleh karena data input untuk piranti lunak model matematik telah ditanggulangi oleh manager proses, kinerja motor sistem dijelaskan pada sub bab teknologi, demikian juga dengan output yang diberikan oleh suatu model matematik.

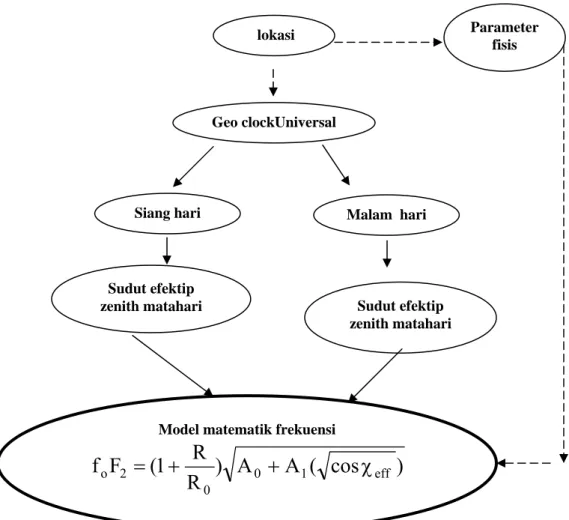
Keuntungan lain dari pustaka matematik adalah setiap implementasi piranti lunak model matematik dapat dikompilasi secara terpisah yang selanjutnya digunakan oleh motor sistem. Akurasi perhitungan yang diperoleh dari model matematik yang digunakan tergantung dari hasil penelitian model matematik yang terus berkembang dari waktu ke waktu. Untuk mengantisipasi hal ini maka struktur model matematik sebagai mesin penghasil informasi dirancang secara sistematis dan fleksibel terhadap perubahan sebagai akibat dari hasil inovasi peneliti dan implementasi model yang baru kepada sistem yang dibangun tidak berpengaruh kepada struktur sistem secara keseluruhan hanya pada titik perubahan itu sendiri. Untuk hal tersebut rincian elemen basis dari model yang membangun sistem secara keseluruhan diperoleh seperti tampak pada Gambar 2.

Pustaka Matematik

Basis Data network

Manager Proses

ISSN 0853 - 0823

Gambar 2. Struktur perhitungan f_oF2

Lokasi, geo clok, sudut efektip zenith matahari dan parameter fisis adalah unsur atau elemen atomik yang membangun model matematik frekuensi sebagai mesin penghasil informasi Dari strukur sistem yang dibangun dapat dilihat bahwa data geo clock merupakan fungsi dari lokasi dan perhitungan waktu lokasi setempat adalah secara universal. Model utama dari sistem ini adalah untuk menghitung frekuensi komunikasi dan frekuensi kritis lapisan F₂. Berdasarkan kepada sifat fisis dari lapiasn tersebut maka perlu dibedakan antara frekuensi antara siang atau malam hari, pada struktur diatas hal ini dinyatakan oleh input sudut zenith matahari untuk siang atau malam hari yang selanjutnya merupakan input untuk model utama ( Stanislawska, 1978).

II. SISTEMATIKA PERHITUNGAN PARAMETER MODEL

Salah satu faktor yang mempengaruhi frekuensi lapisan ionosfer adalah sudut zenith matahari. Untuk lapisan F₂ yang diperhitungkan adalah harga cosinus efektif sudut zenith matahari terhadap lapisan ini yang dibedakan antara siang dan malam hari. Rumusan terhadap parameter ini diperoleh dengan pendekatan secara empiris dengan menggunakan system linear (Deveureux, 1980 ) yang digambarkan oleh blok diagram berikut

Input Output

Gambar 3. Sistem linier persamaan differensial untuk cosinus zenith matahari

lokasi Geo clockUniversal Sudut efektip zenith matahari Parameter fisis

Model matematik frekuensi

)

cos

(

)

1

(

_{0 1} 0 2 eff o

A

A

R

R

F

f

=

+

+

χ

Sudut efektip zenith matahari

Siang hari Malam hari

ISSN 0853 - 0823

Sistem ini dinyatakan oleh persamaan difrensial orde n (Ridger P. ,1990 ) yaitu

0 , ) ( ) ( ) ( ) ( ( 1) 1 ) ( 0 + + + = ≥ − _{t a y t f t t} y a t y a n n n L

dengan a_i adalah konstanta dan a0≠0, dan fungsi f(t) dipandang sebagai input kepada sistem y(t) adalah output atau respond dari sistem. Himpunan dari {_y(_t), _y'(_t), ,_y(n−1)(_t)}

L disebut sebagai

himpunan variabel keadaan dari system, harga dari himpunan fungsi-fungsi ini himpunan fungsi ini pada waktu

t

₀ keadaan system pada keadaan

t

₀. Output y(t)dari system pada waktu t secara khusus ditentukan oleh keadaan system padkaa saat t = 0 dan pengetahuan fungsi input f(s) pada interval

t s≤ ≤

0 Untuk kasus zenith matahari dilakukan pendekatan dengan mengambil f(t)= cosλ, dimana fungsi ini dinyatakan sebagai

cos cos sin{ ( )} T T T Terbit Siang _∆ − π χ = χ (1 )

Dimana Tsunrise adalah waktu saat matahari terbit dan ∆T adalah lama waktu siang hari. Selanjutnya

variabel keadaan dinyatakan oleh himpunan _{{cos eff , (cos eff )}}

dt

d _χ

χ

Jadi permasalahan cosinus zenith selanjutnya dapat dipandang sebagai system linier orde pertama dimana system ini dikendalikan oleh cosχ yang secara eksplisit dinyatakan oleh persamaan differensial berikut

τ_D (cosχ_eff)+cosχ_eff =cosχ dt d ₍₂₎ dan ⎪⎩ ⎪ ⎨ ⎧τ χ = τ 1 . 0 ) cos ( . max 2

0 eff TengahP hari

D

dengan menggunakan transformasi Laplace pada persamaan (2) dan persamaan (1) digunakan sebagai fungsi

cos

χ

diperoleh

⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ α − β + α β + χ = χ ⎟⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎝ ⎛ τ − − cos sin 1 cos ) (cos ₂ D T T hari Tengah Siang eff

pagi

e

(3)

dan , ( ) dan (cos ) cos(L Z₂)

T T T T eff siang Pagi D _{= +} ∆ − π = α ∆ πτ = β

Jika pada persamaan (3) diatas diambil harga T=TTerbit maka harga α menjadi sama dengan

π

dengan demikian diperoleh harga-harga sebagai berikut cosα=cosπ=−1, sinα=sinπ=0 dan

Senja Terbit T

T

T= −

∆

Selanjutnya harga ini disubstitusikan ke dalam persamaan (3) diatas maka diperoleh

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎪ ⎪ ⎭ ⎪ ⎪ ⎬ ⎫ ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ + β β + χ = χ ⎟⎟ ⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎜ ⎝ ⎛ τ − − D T T hari Tengah Senja eff

pagi

e 1 1 cos ) (cos ₂

(4)

Untuk menghindari diskontinuitas tepat sebelum perhitungan cos zenith sesudah matahari terbit maka perhitungan persamaan (3) diperbaiki dengan menambah kondisi sebagai berikut

⎪⎩ ⎪ ⎨ ⎧ χ χ = χ τ − ∆ . ) 24 ( . ) (cos ) (cos . max ) (cos Siang eff N T Senja eff Siang eff e (5)

ISSN 0853 - 0823

Dengan cara yang sama pada persamaan (1) diatas untuk malam hari diperoleh

(

)

(

)

( ) cos cos N TSenja T Senja eff Malam eff e τ − − χ = χ (6) III. HASIL

Parameter : Cosinus effectif zenith mathari Satuan lintang,bujur : Derajat

Lintang : -6.00 Bujur : 106.00

Bulan : April

Waktu : Universal Time Tanggal Jam 01 02 03 04 05 000 0.5629878 0.56541878 0.56791067 0.57045817 0.57305562 001 0.53841484 0.54005474 0.54172325 0.54341471 0.54512304 002 0.49234521 0.49304712 0.49374157 0.49442261 0.49508423 003 0.31204915 0.31151852 0.31099984 0.31049067 0.30998757 004 0.18926737 0.18894553 0.18863095 0.18832211 0.18801697 005 0.11479646 0.11460125 0.11441045 0.11422314 0.11403806 006 0.06962758 0.06950918 0.06939345 0.06927983 0.06916758 007 0.04223126 0.04215945 0.04208925 0.04202034 0.04195226 008 0.02561455 0.025571 0.02552842 0.02548663 0.02544533 009 0.01553601 0.01550959 0.01548377 0.01545842 0.01543337 010 0.00942307 0.00940704 0.00939138 0.00937601 0.00936081 011 0.00571538 0.00570566 0.00569616 0.00568684 0.00567762 012 0.00346655 0.00346066 0.0034549 0.00344924 0.00344365 013 0.00922239 0.0093908 0.00956587 0.0097476 0.00993605 014 0.04171224 0.04228546 0.0428814 0.04350007 0.04414167 015 0.09341434 0.09453906 0.09570794 0.09692092 0.09817823 016 0.15929839 0.16104311 0.16285512 0.16473424 0.16668051 017 0.23389451 0.23625436 0.23870337 0.24124083 0.24386652 018 0.31153771 0.31444204 0.31745324 0.3205702 0.32379207 019 0.38662592 0.38994774 0.39338824 0.39694566 0.4006184 020 0.45387766 0.45744559 0.46113661 0.46494821 0.46887806 021 0.50857657 0.51218808 0.51591891 0.51976591 0.52372575 022 0.54678994 0.55022556 0.55376863 0.55741501 0.56116062 023 0.56554997 0.56858802 0.57171369 0.5749222 0.57820868

ISSN 0853 - 0823

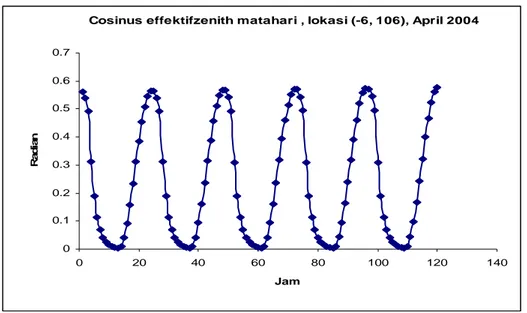
Cosinus effektifzenith matahari , lokasi (-6, 106), April 2004

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0 20 40 60 80 100 120 140 Jam Ra d ia n

Gambar 4. Cosinus zenith matahari pada lokasi (₋6_°,106o) IV. KESIMPULAN

1. Cosinus zenith matahari pada lapisan ionosfer dapat ditentukan secara spasial menggunakan waktu universal.

2. Fungsi zenith matahari terhadap lapisan F₂ ionosfer disuatu lokasi ( lintang dan bujur tergantung pada bulan dan tanggal.

3. Perbedaan harga sudut zenit matahari sebagai fungsi tanggal pada bulan dan jam yang sama relatif dan perbedaan ini akan membesar sesuai dengan pertambahan hari.

4. Pengaruh zenith matahari tertinggi adalah pada jam 10.00 – 14.00 siang hari dan mencapai puncaknya pada tengah hari.

V. DAFTAR PUSTAKA.

Ritger Paul , 1990, Diffrensial Equation with aplication, Mc Graw Hill, new york

Stanislawska, 1978, Instituto Nazionale di Geofisica, 1991, Local Model of the Ionosphere Based Upon Data From Miedzezyn Station, Rome.

E.L. Deveureux,G3CCZ and D. Wilkinson , BSc,CEng, FIERE, G4LEH , RADIO COMMUNICATION 1980

P.H . Levine at al , Minimuf -3 – A simplified hf muf prediction algoritm IEE Conference on antennas & propagation , 1978