Cambridge Pre-U Further Mathematics (9795)
Teks penuh
Gambar
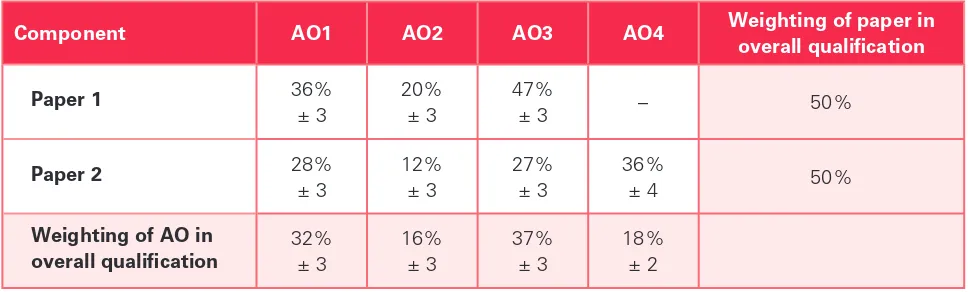
Garis besar
Dokumen terkait
Candidates will demonstrate in-depth knowledge and critical understanding of relevant business theories and concepts and apply this knowledge to business problems and issues
Candidates will demonstrate in-depth knowledge and critical understanding of relevant business theories and concepts and apply this knowledge to business problems and issues
The Pre-U list of mathematical formulae and statistical tables (MF20) has been updated for examinations from June 2017.. The updated version will be issued for
Knowledge of the pure mathematics syllabus content of Cambridge Pre-U Mathematics is assumed for Cambridge Pre-U Short Course in Further
Following an internal review of our Pre-U Further Mathematics papers, we have updated the specimen assessment materials for examination from 2016.. Individual questions in the
> 93% 15 > 87% 14 • correct selection, recall and use of facts, rules, definitions and procedures; comprehension and clear communication of mathematical concepts and techniques;