BAB V STATISTIKA DESKRIPTIF

79

N

Y

N

Y

Y

Y

Y

_n



_i













1 2 3

....



N

Y

N

Y

Y

Y

Y

_n



_i











_{2 3}

....

1

Y

BAB V

STATISTIKA DESKRIPTIF

A. Capaian Pembelajaran

Mahasiswa mampu mengetahui dan memahami serta mengaplikasikan statistika deskriptif ukuran tendensi sentral dan statistika deskriptif ukuran dispersi (sebaran).

B. Indikator Capaian Pembelajaran

1. Kemampuan menggunakan statistik deskriptif ukuran tendensi sentral: rerata (mean), median, modus, midrange.

2. Kemampuan menggunakan statistika deskriptif ukuran dispersi (sebaran): selang, standar deviasi dan varians; koefisien keragaman, kesalahan baku dari rerata (standard error), estimasi selang kepercayaan rerata.

C. Materi

I. UKURAN GEJALA PUSAT ATAU TENDENSI SENTRAL

Disebut ukuran gejala pusat atau tendensi sentral (central tendency), karena nilai atau harga ukuran gejala pusat mampu memberi gambaran tentang posisi atau letak pusat data atau nilai-nilai pengamatan, baik dalam bentuk data terserak, maupun yang sudah dikelompokkan dalam bentuk tabel distribusi frekuensi. Data yang disajikan dengan ukuran-ukuran gejala pusat lebih mudah dibaca dibandingkan dengan data yang masih dalam keadaan terserak.

Posisi atau letak pusat data yang ada dapat dilihat dari besarnya harga rata-rata, modus, median, kuartil, desil, dan persentil.

A. Rata-rata (mean)

Rata-rata (mean) meliputi rata-rata hitung, rata-rata ukur, rata-rata harmonis dan rata-rata tertimbang.

1. Rata-rata hitung (arithmatic mean) a. Rata-rata data terserak

Jika Anda memperoleh data dari kegiatan sensus, maka harga rata-rata yang Anda miliki merupakan rata-rata populasi diberi simbol , apabila Anda memperoleh data dari penelitian sampling, maka datanya merupakan data statistik sampel. Oleh karena itu jika Anda cari rata-ratanya, maka rata-rata tersebut meupakan rata-rata sampel atau rata-rata contoh, dan diberi simbol

Y

(baca Y bar).

Rumus rata-rata populasi () adalah sebagai berikut:

Keterangan:

Yi : data (nilai pengamatan) untuk i = 1,2,3, ... , N

N : banyaknya data/nilai pengamatan (ukuran populasi)

Rumus rata-rata sampel (

Y

): = Keterangan:

Yi : data (nilai pengamatan) untuk i = 1, 2, 3, ...., N N : banyaknya data/nilai pengamatan (ukuran sampel)

Biologi FMIPA Universitas Negeri Malang (State University of Malang)

Email: sulisetijono.fmipa@um.ac.id copyright August 2016

i i i k k k i i f Y f f f f f Y f Y f Y f Y f            .... .... 3 2 1 3 3 2 2

Y

Coba Anda perhatikan contoh penelitian sensus berikut ini.

Setelah berhasil dihasilkan 30 ekor biri-biri melalui kegiatan cloning (kopian), pada usia 1 tahun seluruh biri-biri tersebut didata berat tubuhnya. Ternyata hasilnya sebagai berikut (dalam kg):

78 89 87 69 69 60 62 72 72 72 60 97 66 66 66

78 81 78 88 68 82 84 91 82 98 89 96 82 83 86

Karena merupakan hasil sensus, berarti rata-rata yang akan dihitung adalah rata-rata populasi (). Rata-rata populasi dari N data sebanyak 30 sebesar:

 =

78,3666666

7

kg

30

86

...

69

89

78









_

Bagaimana jika penelitian yang dilakukan merupakan penelitian sampling? Misal 30 ekor biri-biri tersebut merupakan sampel diambil secara acak dari populasi biri-biri hasil cloning sebanyak 100 ekor, berapa rata-ratanya?

Rata-rata sampel (

Y

) dari n data sebanyak 30 adalah:

Y

=

78,3666666

7

kg

30

86

...

69

89

78











b. Rata-rata hitung data yang dikelompokkan

Rumus rata-rata hasil sensus untuk data yang sudah dikelompokkan ke dalam k kelompok adalah sebagai berikut:

Rata-rata populasi ()  = i i i k 3 2 1 k k 3 3 2 2 1 1

f

Y

f

f

....

f

f

f

Y

f

....

Y

f

Y

f

Y

f























Yi : nilai tengah kelas ke-i untuk i = 1, 2, 3, ...., k

fi : frekuensi kelas ke-I, dan fi + f2 + f3 + .... + fk = n

=

Perhatikan contoh penelitian sensus di bawah ini.

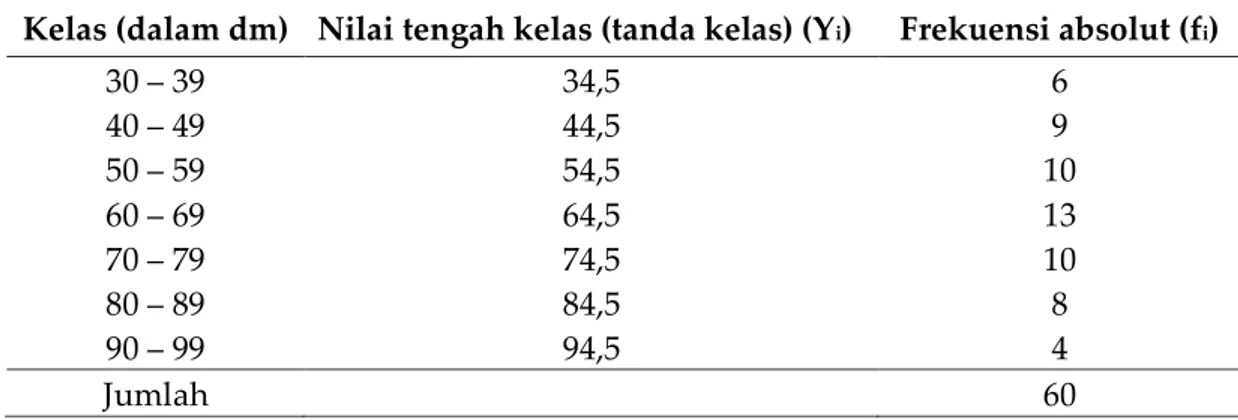
Hasil pendataan tinggi dari seluruh tanaman lamtoro yang tumbuh di pekarangan penduduk desa Minapadi adalah seperti pada Tabel 5.1. Karena seluruh pohon didata, maka rata-rata yang dihitung adalah rata-rata populasi (), yaitu:

=

4

8

10

13

10

9

6

)

5

,

94

(

)

5

,

84

(

8

)

5

,

74

(

10

)

5

,

64

(

13

)

5

,

54

(

10

)

5

,

44

(

9

)

5

,

34

(

6

























 =

60

3790

= 63,16666667 dm

Bagaimana jika data di atas adalah data hasil penelitian sampling? Misalkan 60 pohon tersebut merupakan sebagian dari 600 pohon lamtoro yang ada di desa Minapadi, yang diambil secara acak? Berapakah rata-ratanya?

Y

=

4

8

10

13

10

9

6

)

5

,

94

(

)

5

,

84

(

8

)

5

,

74

(

10

)

5

,

64

(

13

)

5

,

54

(

10

)

5

,

44

(

9

)

5

,

34

(

6

























N

Y

Y

Y

Y

log

log

...

log

_N

log

₁



₂



₃





N N Y Y Y Y₁. ₂. ₃...

N

Y

_i

log



n

Y

_i

log



G

Y

n n Y Y Y Y₁. ₂. ₃...

Y

=

60

3790

= 63,16666667 dm

Tabel 5.1 Hasil Pengukuran Tinggi Tanaman Lamtoro di Pekarangan Penduduk Desa Minapadi

Kelas (dalam dm) Nilai tengah kelas (tanda kelas) (Yi) Frekuensi absolut (fi)

30 – 39 34,5 6 40 – 49 44,5 9 50 – 59 54,5 10 60 – 69 64,5 13 70 – 79 74,5 10 80 – 89 84,5 8 90 – 99 94,5 4 Jumlah 60

2. Rata-rata ukur (Geometric mean)

Rata-rata ukur (Geometric mean) merupakan rata-rata nilai/harga pengamatan yang dihitung atas dasar akar banyaknya nilai/harga pengamatan dari hasil perkalian seluruh data. Sajian rata-rata ukur akan lebih baik dibandingkan rata-rata hitung jika merupakan data yang menunjukkan urutan perubahan yang tetap atau hampir tetap. Misalnya, data kenaikan atau penurunan dari sesuatu hal.

a. Rata-rata ukur data terserak

Untuk mencari rata-rata ukur dari data yang masih terserak digunakan rumus sebagai berikut:

Rata-rata ukur populasi (G) G =

Atau log G =

disingkat menjadi: log G =

Keterangan:

Yi : data (nilai pengamatan) untuk i = 1, 2, 3, ..., N

N : banyaknya data/nilai pengamatan ukuran (populasi) Rata-rata ukur sampel (

Y

G) =

atau log

Y

G =

n

Y

log

...

Y

log

Y

log

Y

log

₁



₂



₃





_n

disingkat menjadi: log

Y

G =

Keterangan:

Yi : data (nilai pengamatan) untuk i = 1, 2, 3, ..., n

n : banyaknya data/nilai pengamatan (ukuran sampel) Coba anda perhatikan contoh penelitian sensus di bawah ini.

Hasil sensus berat badan 30 ekor biri-biri usia 1 tahun hasil cloning (kembaran) menunjukkan kenaikan rata-rata berat triwulan I sebanyak 10 kg, triwulan II sebanyak 15

i i i

f

Y

f





(

log

)

i i i

f

Y

f





(

log

)

3 .... 11 9 5 5 , 94 log 3 .... 5 , 54 log 11 5 , 44 log 9 5 , 34 log 5        

15 kg, triwulan III sebanyak 22,5 kg, dan triwulan IV sebanyak 15 kg. bErap rata-rata kenaikan badan per triwulan?

Kenaikan triwulan II = 15/10 x triwulan I = 1,50 kali Kenaikan triwulan III = 22,5/15 x triwulan II = 1,50 kali Kenaikan triwulan IV = 15/22,5 x triwulan III = 0,67 kali

Jika dihitung dengan menggunakan rumus rata-rata hitung populasi ():

 =

3

67

,

0

50

,

1

50

,

1





= 1,22 kali

Jika dihitung dengan menggunakan rumus rata-rata ukur populasi (G):

G = 3

(

1

,

50

)(

1

,

50

)(

0

,

67

)

= 1,15 atau log G =

3

67

,

0

log

50

,

1

log

50

,

1

log





= 0,17825732/3 = 0,059419106 kali sehingga G = antilog 0,059419106 = 1,146618929 kali = 1,15 kali

Jika data tersebut merupakan data hasil penelitian sampling, berarti notasinya tinggal diganti dengan notasi untuk sampel, sedang hasilnya akan tetap sama.

b. Rata-rata ukur yang dikelompokkan

Untuk mencari rata-rata ukur dari data yang sudah dikelompokkan dapat digunakan rumus sebagai berikut:

Rata-rata ukur populasi  log G =

Keterangan:

Yi : nilai tengah kelas ke-i = 1, 2, 3, ...., k

fi : frekuensi kelas ke-i, dan fi + f2 + f3 + .... + fk = N

Rata-rata ukur sampel (

Y

G)  log

Y

G =

Keterangan:

Yi : nilai tengah kelas ke-i untuk i = 1, 2, 3, ..., k

fi : frekuensi kelas ke-i dan f1 + f2 + f3 + ... + fk = n

Untuk penelitian sensus perhatikan contoh di bawah ini.

Hasil pengukuran terhadap pertambahan tinggi 60 tanaman lamtoro yang ada di pekarangan penduduk Desa Minapadi setelah disusun dalam bentuk tabel distribusi frekuensi tampak pada Tabel 5.2.

Jika dihitung dengan menggunakan rata-rata hitung ()  =

3

....

11

9

5

)

5

,

94

(

3

....

)

5

,

54

(

11

)

5

,

44

(

9

)

5

,

34

(

5

















=

60

3780

= 63,0 cm Jika dihitung dengan menggunakan rata-rata geometri (G):

log G =

= = 1,783819018

N

Y

Y

Y

Y

N

1

....

1

1

1

3 2 1









Tabel 5.2 Hasil Pertambahan Tinggi Tanaman Lamtoro Selama 1 Bulan yang Tumbuh di Pekarangan Penduduk Desa Minapadi

Kelas (dalam cm) Nilai tengah kelas (tanda kelas) (Yi) Frekuensi absolut (fi)

30 – 39 34,5 5 40 – 49 44,5 9 50 – 59 54,5 11 60 – 69 64,5 13 70 – 79 74,5 12 80 – 89 84,5 7 90 – 99 94,5 3 Jumlah 60

3. Rata-rata harmonis (harmonic mean)

Rata-rata harmonis (harmonic mean) adalah rata-rata yang diperoleh dengan cara mencari kebalikan atau invers dari datanya. Rata-rata harmonis biasa digunakan untuk mencari rata-rata dari banyak hal yang berbeda kualitasnya.

Rata-rata harmonis populasi (H):

(H) = Keterangan:

Yi : data(nilai pengamatan untuk i = 1, 2, 3, ...., N

N : banyaknya data/nilai pengamatan (ukuran populasi) Rata-rata harmonis sampel (

Y

H):

Y

H =

Keterangan :

Yi : data(nilai pengamatan untuk i = 1, 2, 3, ...., N

N : banyaknya data/nilai pengamatan (ukuran populasi) Coba Anda perhatikan contoh penelitian sensus berikut ini.

Seluruh luas lahan padi di Desa Minapadi 15300 ha. Setelah lahan dibagi menjadi 5 bagian, dan tiap bagian ditanami padi Cisadane, IR-28, VUTW, Rajalele dan Cianjur, hasilnya seperti pada Tabel 5.3.

Tabel 5.3 Hasil Produksi Padi Desa Minapadi menurut Kultivarnya Kultivar padi Luas lahan (ha) Produksi/ha (ton) Produksi total (ton)

Cisadane 3.060 7,4 22.644

IR-26 3.060 6,7 20.502

VUTW 3.060 6,6 20.196

Rajalele 3.060 5,7 17.442

Cianjur 3.060 6,5 19.890

Jika rata-rata produksi padi tiap bagian dicari dengan rata-rata hitung ():  =

5

890

.

18

442

.

17

196

.

20

502

.

20

644

.

22









= = 20.134,8 ton

atau:  =

5

5

,

6

7

,

5

6

,

6

7

,

6

4

,

7









= 6,58 ton/ha Jika dicari dengan rata-rata harmonis (H):

H =

890

.

19

1

442

.

17

1

196

.

20

1

502

.

20

1

644

.

22

1

5









= 19.995,07 ton atau H =

5

,

6

1

7

,

5

1

6

,

6

1

7

,

6

1

4

,

7

1

5









= 6,534 ton

4. Rata-rata tertimbang (weighted mean)

Rata-rata tertimbang (weighted mean) adalah rata-rata yang dicari dengan mempertimbangkan tingkat pentingnya kelompok-kelompok datanya.

Rata-rata tertimbang populasi (W) W = i i i k 3 2 1 k k 3 3 2 2 1 1

N

Y

N

N

....

N

N

N

Y

N

....

Y

N

Y

N

Y

N























Keterangan:

Yi : data (nilai pengamatan) untuk i = 1, 2, 3, ...., k

N : banyaknya data (nilai pengamatan) untuk i = 1, 2, 3, ...., k Rata-rata tertimbang sampel (

Y

W):

W

Y

= i i i k 3 2 1 k k 3 3 2 2 1 1

n

Y

n

n

....

n

n

n

Y

n

....

Y

n

Y

n

Y

n























Yi : data (nilai pengamatan) untuk i = 1, 2, 3, ...., k

n : banyaknya data (nilai pengamatan) untuk i = 1, 2, 3, ...., k

Coba Anda perhatikan contoh penelitian sensus ini. Produktivitas tanaman padi berdasarkan kultivarnya dari seluruh lahan yang ada di Desa Minapadi berdasarkan kultivarnya dari seluruh lahan yang ada di Desa Minapadi ditampilkan pada Tabel 5.4. Tabel 5.4 Hasil Produksi Desa Minapadi menurut Kultivarnya

Jenis padi Luas lahan (ha) Produksi/ha (ton) Produksi total (ton)

Cisadane 1.200 7,4 22.644 IR-26 4.100 6,7 20.502 VUTW 3.300 6,6 20.196 Rajalele 700 5,7 17.442 Cianjur 2.500 6,5 19.890 C-4 3.000 7,0 21.000 Ketan 500 5,6 2.800 Jumlah 15.300 102.170

Kalau dihitung harga rata-rata produksi padi dengan menggunakan rata-rata hitung ():  =

7

6

,

5

0

,

7

5

,

6

7

,

5

6

,

6

7

,

6

4

,

7













= 6,5 ton/ha

Jika dihitung dengan menggunakan rata-rata tertimbang (W): W =

500

....

300

.

3

100

.

4

200

.

1

)

6

,

5

)(

500

(

....

)

6

,

6

)(

300

.

3

(

)

7

,

6

)(

100

.

4

(

)

4

,

7

)(

200

.

1

(

















= 6,677777778 ton/ha B. Modus

Modus adalah data yang memiliki frekuensi pemunculan terbanyak. Oleh karena itu, cara mencari modus dapat dilihat dari berapa kali suatu data muncul di antara seluruh data yang ada.

1. Menentukan modus data terserak

Agar lebih mudah melacaknya, data diurutkan dari yang terkecil ke yang terbesar atau sebaliknya.

Coba Anda perhatikan contoh penelitian sampling ini. Hasil pengukuran berat 30 ekor biri-biri yang diambil secara acak dari populasi biri-biri hasil cloning sebanyak 100 ekor, adalah sebagai berikut (dalam kg):

78 89 87 69 69 60 62 72 72 72 60 97 66 66 66 78 81 78 88 68 82 84 91 82 98 89 96 82 83 86

Agar dapat dicari modusnya, data tersebut harus diurutkan dari yang terbesar ke yang terkecil. Hasilnya adalah sebagai berikut:

98 97 96 91 89 89 88 87 86 84 83 82 82 82 81 78 78 78 72 72 72 69 69 68 66 66 66 62 60 60

Data sebesar 82,78, 72 dan 66 muncul tiga kali. Dengan demikian, sebaran data di atas memiliki empat modus yakni 82, 78, 72 dan 66. Dengan kata lain data di atas merupakan data tetramodal, sehingga termasuk data multimodal.

2. Menentukan modul data yang dikelompokkan

Modus untuk data yang sudah dikelompokkan dapat dihitung dengan rumus sebagai berikut: Mo =

_















2 1 1

s

s

s

C

L

Keterangan:

L : batas bawah (lower class boundary) kelas yang mengandung modus (kelas yang memiliki frekuensi terbesar).

s1 : selisih frekuensi kelas yang mengandung modus dengan frekuensi kelas

dibawahnya.

s2 : selisih frekuensi kelas yang mengandung modus dengan frekuensi kelas di atasnya.

C : panjang kelas atau selang kelas (selisih harga batas bawah dengan batas atas kelas) Sebagai contoh perhitungan, perhatikan data penelitian sampling hasil pengukuran tinggi 60 batang tanaman lamtoro yang ada di pekarangan penduduk Desa Minapadi seperti pada Tabel 5.5.

















m kb n

f

f

C

L

0

,

5

_















m n ka

f

f

C

U

( )

0

,

5

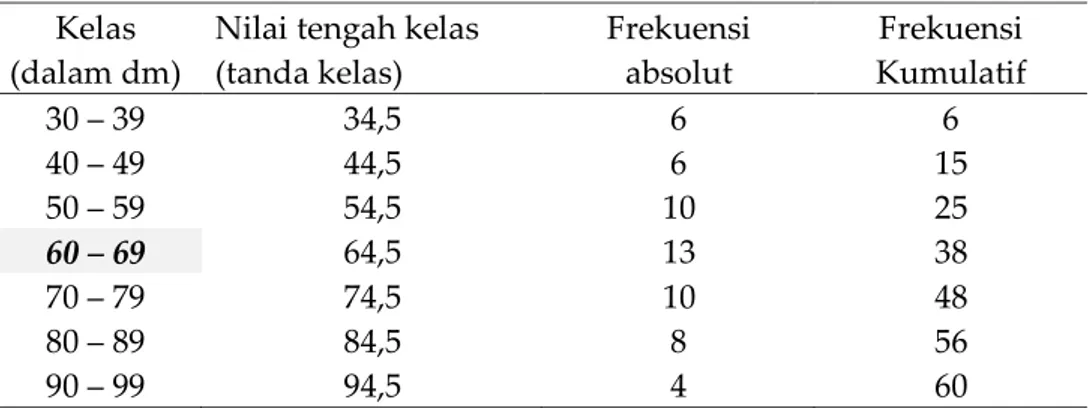
Tabel 5.5 Hasil Pengukuran Tinggi Tanaman Lamtoro di Desa Minapadi

Kelas (dalam dm)

Nilai tengah kelas (tanda kelas) Frekuensi absolut Frekuensi Kumulatif 30 – 39 34,5 6 6 40 – 49 44,5 6 15 50 – 59 54,5 10 25 60 – 69 64,5 13 38 70 – 79 74,5 10 48 80 – 89 84,5 8 56 90 – 99 94,5 4 60

Coba Anda perhatikan, kelas yang manakah yang mengandung modus? Carilah kelas yang frekuensinya terbanyak, dan ternyata kelas 60–69. Oleh karena itu cari harga batas bawah kelasnya (L). L dari kelas 60 – 69 = 59,5 s1 : 13 – 10 = 3 s2 : 13 – 10 = 3 C: 39,5 – 29,5 = 10 Mo = 59,5 + 10

_



_





3

3

3

= 64,5 C. Median

Median adalah suatu nilai yang membagi data yang telah diurutkan besarnya dari yang terbesar sampai yang terkecil atau sebaliknya), menjadi dua kelompok data, yakni dara kelompok atas dan data kelompok bawah dengan anggota yang sama banyaknya.

1. Menentukan median data terserak

Agar lebih mudah melacak posisi median, data perlu diurutkan dari yang terkecil ke yang terbesar atau sebaliknya. Kemudian cari posisi atau letak median dengan rumus:

Posisi Me = (N + 1)/2 untuk data sensus

atau Posisi Me = (n + 1)/2 untuk posisi data sampling

Seteah diperoleh posisi median, Anda akan dapat mempeoleh harga mediannya.

Coba perhatikan contoh berikut ini. Dari hasil penelitian sampling berupa pengukuran berat terhadap 30 ekor biri-biri yang diambil secara acak dari populasi biri-biri hasil cloning sebanyak 100 ekor yang telah dihitung modusnya, sekarang carilah mediannya. Perhatikan datanya.

78 89 87 69 69 60 62 72 72 72 60 97 66 66 66 78 81 78 88 68 82 84 91 82 98 89 96 82 83 86

Setelah diurutkan dari yang terbesar ke yang terkecil terlihat sebagai berikut: 98 97 96 91 89 89 88 87 86 84 83 82 82 82 81

78 78 78 72 72 72 69 69 68 66 66 66 62 60 60

Karena data sampling, berarti banyaknya data (n) = 30.

Berarti posisi median (Me) = (n + 1)/2 = (30+1) = 15,5. Data ke 15 = 81; data ke-16 = 78, berarti Me = (81+78)/2 = 79,5 kg

2. Menentukan median data yang dikelompokkan

Median untuk data yang sudah dikelompokkan dapat dihitung dengan rumus sebagai berikut:

Me = , atau Me = Keterangan :

L : batas bawah (lower class boundary) kelas yang mengandung median (kelas yang mengandung datum ke (n + 1)/2 dari n data)

U : batas atas kelas (upper class boundary) yang mengandung median C : panjang kelas atau selang kelas

n atau N : banyaknya data, n untuk data sampling dan N data sensus.

fkb : frekuensi kumulatif kelas di bawah kelas yang mengandung median. fka : frekuensi kumulatif kelas di kelas yang mengandung median. fm : frekuensi absolut kelas yang mengandung median.

Sebagai contoh coba perhatikan hasil penelitian sensus terhadap tinggi tanaman lamtoro di Desa Morangan yang tersaji pada Tabel 5.6.

Tabel 5.6 Hasil Sensus Tinggi Tanaman Lamtoro di Desa Morangan

Kelas (dalam dm)

Nilai tengah kelas (tanda kelas)

Frekuensi absolut Frekuensi Kumulatif 30 – 39 34,5 16 16 40 – 49 44,5 29 45 50 – 59 54,5 30 75 60 – 69 64,5 53 128 70 – 79 74,5 32 160 80 – 89 84,5 25 185 90 – 99 94,5 15 200

Oleh karena 200 tanaman lamtoro diamati semua berarti merupakan data sensus, maka banyaknya data (N) = 200. Posisi median sebelum data diurutkan = (N + 1)/2 = (200 + 1)/2 = 100,5, dengan demikian kelas yang mengandung median adalah kelas 60-69, sehingga:

L: 59,5 U : 69,5 C : 10 fkb : 75 fka: 128 fm: 53 Me =  _  _ 53 75 ) 200 ( 5 , 0 10 5 , 59 = 64,22 dm atau Me =  _  _ 53 ) 200 ( 5 , 0 128 10 5 , 69 = 64,22 dm D. Kuartil

Kuartil adalah tiga buah nilai yang membagi data yang telah diurutkan besarnya, menjadi empat kelompok data dengan anggota yang sama banyaknya. Karena kuartil membagi menjadi 4 kelompok sama banyak, maka harga kuartil kedua akan sama dengan harga median. 1. Menentukan kuartil data yang terserak

Untuk memperoleh harga kuartil I, kuartil II dan kuartil III, data harus diurutkan terlebih dahulu dari yang terkecil ke yang terbesar. Kemudian dicari lebih dahulu posisi atau letak masing-masing kuartil, baru dapat diperoleh harganya.

Mula-mula cari kuartil II atau mediannya, misalkan n = 61, maka (n + 1)/2 = 31. Jadi kuartil II adalah data urutan ke 31. Mengapa? Karena data urutan ke 31 membagi data menjadi dua kelompok, masing-masing beranggotakan 30 data. Kelompok I beranggotakan data ke 1 sampai data ke 30, dan kelompok II beranggotakan data ke 32 sampai data ke 61. Posisi kuartil I akan membagi kelompok I menjadi dua kelompok yang anggota sama banyak. Karena anggota kelompok I sebanyak 30, berarti kuartil I = (n + 1)/2 = (30 + 1)/2 = 15. Jadi kuartil I berada diantara data urutan ke 15 dan data urutan ke 16. Kuartil III = (n + 1)/2 = (30 + 1)/2 = 15,5, tetapi urutan data kelompok II dimulai dari urutan ke 32 dan seterusnya sampai urutan ke 61. Karena data pertama pada posisi urutan ke 32, maka posisi kuartil III pada urutan 15,5 berada diantara data urutan ke 46 dan data urutan ke 47.

















m kb n

f

f

C

L

0

,

75

















m kb n

f

f

C

L

0

,

25

2. Menentukan kuartil data yang dikelompokkan

Untuk data yang telah dikelompokkan, harga kuartilnya dapat dihitung dengan rumus sebagai berikut.

Kuartil I atau K1 dicari dengan rumus: K1 =

Kuartil II sama dengan median. Bagaimana dengan kuartil III? Kuartil III atau K3 dicari dengan rumus: K3 =

Keterangan:

L : batas bawah (lower class boundary) kelas yang mengandung kuartil yang dimaksudkan.

C : panjang kelas atau selang kelas.

n atau N : banyaknya data, n untuk data sampling dan N untuk data sensus.

fkb : frekuensi kumulatif kelas di bawah kelas yang mengandung kuartil yang dimaksudkan.

fm : frekuensi absolut kelas yang mengandung kuartil yang dimaksudkan.

Sebagai contoh perhitungan, perhatikan kembali data penelitian sampling hasil pengukuran tinggi 60 batang tanaman lamtoro yang diambil secara acak dari 600 tanaman lamtoro yang ada di pekarangan penduduk Desa Minapadi yang disajikan pada Tabel 5.6 yang sudah dihitung harga modusnya. Oleh karena data hasil penelitian sampling, maka banyaknya data (n) = 60. Oleh ketiga kuartil, data terkelompokkan menjadi 4 kelompok, masing-masing beranggotakan 15 data.

Kelas (dalam dm)

Nilai tengah kelas (tanda kelas)

Frekuensi absolut Frekuensi Kumulatif 30 – 39 34,5 16 16 40 – 49 44,5 29 45 50 – 59 54,5 30 75 60 – 69 64,5 53 128 70 – 79 74,5 32 160 80 – 89 84,5 25 185 90 – 99 94,5 15 200

Mencari harga kuartil I (K1):

Posisi kuartil I di urutan ke 15,5 atau antara datake 15 dan data ke 16. Jadi kelas yang mengandung kuartil I adalah kelas 50 – 59. Dengan demikian:

L : 49,5 C : 10 fkb : 15 fm : 10 K1 =













10

15

)

60

(

25

,

0

10

5

,

49

= 49,5 dm

Posisi kuartil II di urutan ke 30,5 atau antara data ke 30 dan data ke 31. Jadi kelas yang mengandung kuartil II adalah kelas 60 – 69. Dengan demikian:

L : 59,5 C : 10 fkb : 25 fm : 13 K2 =













13

25

)

60

(

5

,

0

10

5

,

59

= 63,35 dm

Posisi kuartil III di urutan ke 45,5 atau antara data ke 45 dan data ke 46. Jadi kelas yang mengandung kuartil III adalah kelas 70 – 79. Dengan demikian:

L : 59,5 C : 10 fkb : 38 fm : 13 K3 =













13

38

)

60

(

75

,

0

10

5

,

69

= 74,88 dm

E. Desil

Desil adalah sembilan buah nilai yang membagi data yang telah diurutkan besarnya, menjadi sepuluh kelompok data dengan anggota yang sama banyaknya. Oleh karena itu, harga desil kelima (Dv) akan sama dengan harga mediannya. Agar dapat dikelompokkan menjadi 10 kelompok, maka banyaknya data juga harus berkelipatan 10.

a. Menentukan desil data terserak

Mula-mula data dibagi dua untuk mencari desil V atau mediannya. Misal, banyaknya data 60. Posisi desil V = (n + 1)/2 = (60 + 1)/2 = 30,5. Dengan demikian desil V berada di antara data urutan ke 30 dan data urutan ke 31. Kemudian kelompok pertama harus dibagi lagi menjadi lima kelompok, demikian pula kelompok yang kedua. Kelompok pertama yang beranggotakan 30 data, jika dibagi menjadi lima kelompok, masing-masing akan beranggotakan enam data. Dengan demikian, desil I (D1) di urutan 6,5 atau antara data ke 6 dan ke 7. Desil II (D2) di urutan 12,5 atau antara data ke 12 dan ke 13.

Di mana posisi desil V? Desil V (D5) di urutan 30,5 atau antara data ke 30 dan ke 31. Demikian pula untuk kelompok kedua, jika dibagi lagi menjadi lima kelompok masing-masing juga beranggotakan enam data. Oleh karena itu, desil VI (D6) diurutan 36,5 atau antara data ke 36 danke 37. Di mana posisi desil IX? Desil IX (D9) di urutan 54,5 atau antara data ke 54 dan ke 60.

b. Menentukan desil data yang dikelompokkan Desil I atau D1 dicari dengan rumus:

D1 =

















m kb n

f

f

10

,

0

C

L

Desil II atau D2 dicari dengan rumus:

D2 =

















m kb n

f

f

20

,

0

C

L

Bagaimana dengan desil IX atau D9? Desil IX dapat dihitung dengan rumus:

D9 =

















m kb n

f

f

90

,

0

C

L

Keterangan:

L : batas bawah (lower class boundary) kelas yang mengandung desil yang dimaksudkan.

C : panjang kelas atau selang kelas.

n atau N : banyaknya data, n untuk data sampling dan N untuk data sensus.

fkb : frekuensi kumulatif kelas di bawah kelas yang mengandung desil yang dimaksudkan.

fm : frekuensi absolut kelas yang mengandung desil yang dimaksudkan. F. Persentil

Persentil adalah 99 buah nilai yang membagi data yang telah diurutkan besarnya, menjadi 100 kelompok data dengan anggota yang sama banyaknya. Dengan demikian, harga persentil ke 50 akan sama dengan harga mediannya. Agar dikelompokkan menjadi 100 kelompok tentunya data harus cukup banyak, yakni merupakan kelipatan 100.

Untuk data yang telah dikelompokkan, besarnya persentil dapat dihitung dengan rumus sebagai berikut:

P1 =

















m kb n

f

f

01

,

0

C

L

Persentil kedua atau P2 dicari dengan rumus:

P2 =

















m kb n

f

f

02

,

0

C

L

Bagaimana dengan desil IX atau D9? Desil IX dapat dihitung dengan rumus:

D99 =

















m kb n

f

f

99

,

0

C

L

Keterangan:

L : batas bawah (lower class boundary) kelas yang mengandung persentil yang dimaksudkan.

C : panjang kelas atau selang kelas.

n atau N : banyaknya data, n untuk data sampling dan N untuk data sensus. fkb : frekuensi kumulatif kelas di bawah kelas yang mengandung persentil

yang dimaksudkan.

fm : frekuensi absolut kelas yang mengandung persentil yang

dimaksudkan.

LATIHAN

1. Jelaskan mengapa nilai rata-rata, modus dan median mampu menjadi ukuran gejala pusat!

2. Jelaskan perbedaan nilai rata-rata hitung, rata-rata ukur, rata-rata tertimbang dan rata-rata harmonis!

3. Jelaskan bagaimana prosedur mencari kuartil untuk data terserak!

4. Data yang bagaimanakah yang dapat dicari harga desil dan persentilnya!

RANGKUMAN

1. Data yang terserak sangat sukar untuk diinterpretasi. Oleh karena itu perlu disajikan secara terorganisasi.

2. Ukuran gejala pusat mampu memberikan informasi yang lebih komunikatif dalam kita membaca data daripada masih berwujud data terserak ataupun jika sudah dikelompokkan ke dalam distribusi frekuensi.

3. Dengan melihat besarnya ukuran gejala pusatnya, kita dapat mengetahui deskripsi atau gambaran yang utuh dari kondisi populasi atau sampel yang kita teliti, apalagi jika sudah dilengkapi dengan ukuran penyimpangannya.

II.

UKURAN PENYIMPANGAN ATAU VARIABILITAS

Ukuran penyimpangan atau ukuran variabilitas disebut pula ukuran dispersi, karena merupakan ukuran yang mampu memberi gambaran tentang besar kecilnya data terhadap rata-ratanya. Ukuran penyimpangan juga menunjukkan keberagaman harga data atau nilai pengamatan. Semakin besar ukuran penyimpangannya berarti semakin besar tingkat keberagaman harga data atau nilai pengamatan. Semakin besar ukuran peyimpangannya berarti semakin besar tingkat keberagaman harga data yang kita miliki. Oleh karena itu, dengan

Kisaran atau rentang (R) = nilai pengamatan terbesar – nilai pengamatan terkecil

n Y Y_i





diberikannya ukuran gejala pusat beserta ukuran penyimpangan atau ukuran variabilitas/ dispersinya, akan dapat diperoleh gambaran yang lengkap tentang keadaan data tersebut.

Untuk lebih mudah memperoleh gambarannya, dapat dilihat dari ilustrasi sebagai berikut: Dua induk ayam sama-sama memiliki 3 anak. Ketiga anak ayam dari induk pertama masing-masing beratnya 3 ons, 4 ons, dan 5 ons. Anak dari induk kedua masing-masing beratnya 3,5 ons, 4 ons, dan 4,5 ons. Kalau dicari reratanya, maka rerata (rata-rata) masing-masing kelompok anak ayam tersebut 4 ons. Namun demikian, jika dilihat berat tiap ekornya, ketiga anak ayam dari induk pertama kurang seragam dibanding ketiga anak dari induk yang kedua. Oleh karena itu, kalau informasi yang disampaikan hanya ukuran gejala pusatnya, dalam hal ini berupa reratanya, belum dapat memberi gambaran sepenuhnya terhadap keadaan berat anak ayam dari kedua induk tersebut.

Besarnya penyimpangan data dari rata-ratanya dapat dilihat dari harga kisaran atau rentangan (range), simpangan rata-rata (mean deviation), simpangan baku (standard deviation), varians/ragam (variance), dan koefisien variasi (coeffisien of variability/coeffisien of variation). A. RENTANG ATAU KISARAN (RANGE)

Rentang atau kisaran (range) adalah selisih antara nilai pengamatan terkecil

dengan nilai pengamatan terbesar dari suatu data.

Sebagai contoh, perhatikan data hasil sensus terhadap 30 ekor biri-biri usia 1 tahun hasil cloning (kembaran) yang menunjukkan berat badan sebagai berikut (dalam kg):

78 89 87 69 69 60 62 72 72 72 60 97 66 66 66 78 81 78 88 68 82 84 91 82 98 89 96 82 83 86

Nilai atau harga data terkecil 60 dan data terbesar 98, maka rentang/kisaran data (R) = 98 – 60 = 28.

B. SIMPANGAN RATA-RATA ATAU DEVIASI RATA-RATA (mean

deviation)

Simpangan atau deviasi adalah jumlah dari harga mutlak selisih antara setiap data dengan reratanya. Jika simpangan atau deviasi tersebut dibagi dengan banyaknya data (N untuk populasi atau n untuk sampel), maka akan diperoleh rerata simpangan (simpangan rata-rata) atau deviasi rata-rata. Untuk simpangan rata-rata tidak ada notasi khusus.

1. Mencari rerata simpangan dari data terserak

Rumus rerata simpangan atau rerata deviasi populasi adalah sebagai berikut: Rerata simpangan populasi =

N

Y

_i







Keterangan:

 : rerata populasi

Yi : data (nilai pengamatan) ke-i untuk i = 1, 2, 3, …., N

N : banyaknya data atau ukuran populasi

Rumus simpangan rata-rata atau deviasi rata-rata sampel adalah sebagai berikut: Simpangan rata-rata sampel =

Y

: rata-rata sampel

Yi : data (nilai pengamatan) ke-i untuk i = 1, 2, 3, …., N

N : banyaknya data (nilai pengamatan)

Coba anda perhatikan contoh penghitungan rerata simpangan untuk hasil penelitian sensus berikut ini. Hasil sensus terhadap 30 ekor biri-biri usia 1 tahun hasil cloning (kembaran) menunjukkan berat adalah sebagai berikut (dalam kg).

78 89 87 69 69 60 62 72 72 72 60 97 66 66 66 78 81 78 88 68 82 84 91 82 98 89 96 82 83 86 Jika dibuat tabel akan tersaji pada Tabel 5.7.

Tabel 5.7 Data Sensus Berat Biri-Biri Hasil Cloning Usia Satu Tahun (Dalam kg) Pengamatan ke Berat biri-biri (kg) Yi Penyimpangan

Y

_i





1 78 0,36666667 2 89 10,63333333 3 87 8,63333333 4 69 9,36666667 5 69 9,36666667 6 60 18,36666667 7 62 16,36666667 8 72 6,36666667 9 72 6,36666667 10 72 6,36666667 11 60 18,36666667 12 97 18,63333333 13 66 12,36666667 14 66 12,36666667 15 66 12,36666667 16 78 0,36666667 17 81 2,63333333 18 78 0,36666667 19 88 9,63333333 20 68 10,36666667 21 82 3,63333333 22 84 5,63333333 23 91 12,63333333 24 82 3,63333333 25 98 19,63333333 26 89 10,63333333 27 96 17,63333333 28 82 3,63333333 29 83 4,63333333 30 86 7,63333333 Jumlah 2351 279,0  Yi 

Y

_i





i i i f Y f   



i i i

f

Y

Y

f







i i f Y   



30 279

Oleh karena hasil sensus maka harus digunakan rumus untuk populasi, sehingga harga rerata populasi ():  = 30 2351   N Yi

= 78,36666667 kg. Sedangkan rerata simpangan atau rerata deviasi populasi: Simpangan rata-rata populasi = = = 9,3 kg

2. Mencari rerata simpangan atau rerata deviasi populasi

Rerata simpangan populasi untuk data yang sudah dikelompokkan dapat dicari dengan menggunakan rumus berikut:

Rerata simpangan populasi = Keterangan:

 : rata-rata populasi

Yi : nilai tengah kelas ke-i untuk I = 1, 2, 3, ….., k fi : frekuensi kelas ke-i, dan f1 + f2 + f3 + …. + fk = N N : banyaknya data (ukuran populasi)

Rerata simpangan sampel (RS) Simpangan rata-rata sampel = Keterangan:

Y

: rata-rata populasi

Yi : nilai tengah kelas ke-i untuk I = 1, 2, 3, ….., k fi : frekuensi kelas ke-i, dan f1 + f2 + f3 + …. + fk = n n : banyaknya data (ukuran sampel)

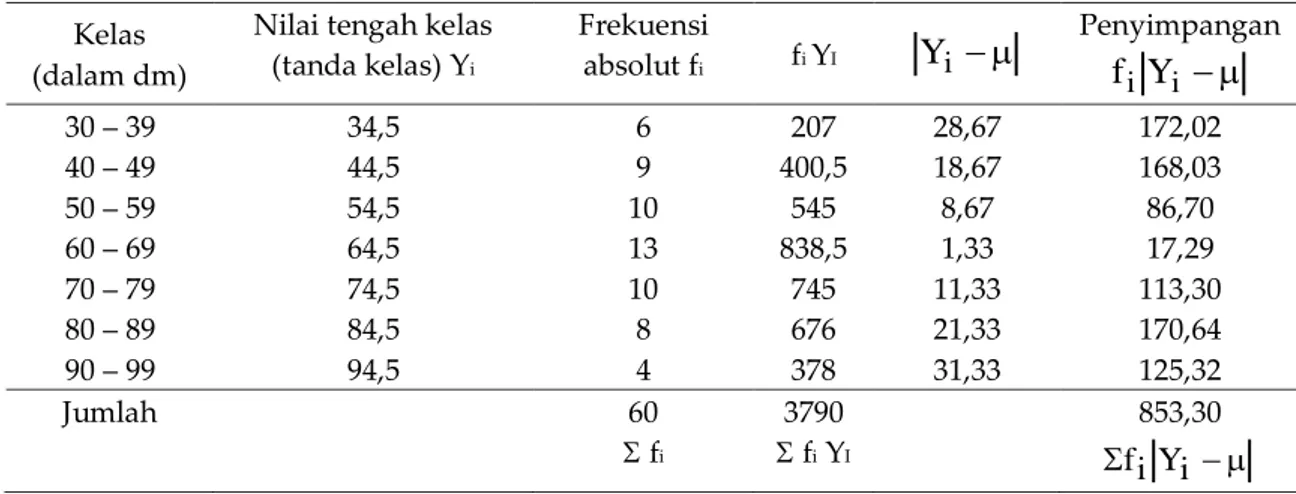
Tabel 5.8 adalah contoh perhitungan untuk mencari rerata simpangan dari yang sudah terkelompokkan dari hasil-hasil sensus terhadap seluruh tanaman lamtoro yang tumbuh di pekarangan penduduk Desa Dadapan yakni sebanyak 60 batang.

Harga rerata populasi () dari N data sebanyak 60 buah dan yang sudah dikelompokkan menjadi 7 kelas tersebut adalah:

 = i i i

f

Y

f





=

60

3790

= 63,17

Besarnya simpangan rata-rata atau deviasi rata-rata populasi: Besarnya rata-rata populasi =

i i i

f

)

Y

(

f









=

60

30

,

853

= 14,22

Tabel 5.8 Hasil Sensus terhadap Pengukuran Tinggi Tanaman Lamtoro di Pekarangan Penduduk Desa Dadapan

Kelas (dalam dm)

Nilai tengah kelas (tanda kelas) Yi Frekuensi absolut fi fi YI

Y

i





Penyimpangan





i i

Y

f

30 – 39 34,5 6 207 28,67 172,02 40 – 49 44,5 9 400,5 18,67 168,03 50 – 59 54,5 10 545 8,67 86,70 60 – 69 64,5 13 838,5 1,33 17,29 70 – 79 74,5 10 745 11,33 113,30 80 – 89 84,5 8 676 21,33 170,64 90 – 99 94,5 4 378 31,33 125,32 Jumlah 60 3790 853,30  fi  fi YI   i Y i f

C. Simpangan baku atau deviasi standar (standard deviation)

Disebut simpangan baku atau deviasi standar karena ukuran ini menunjukkan standar penyimpangan dari rata-ratanya. Dalam menyajikan gambaran penyimpangan yang terjadi, lebih umum disajikan harga simpangan baku atau standar deviasinya daripada ukuran simpangan rata-ratanya.

Kalau dalam perhitungan simpangan rata-rata dengan memberikan harga mutlak untuk menghilangkan harga negatif selisih masing-masing data dengan rata-ratanya, maka pada perhitungan simpangan baku atau standar deviasi dilakukan dengan cara mengkuadratkan selisih masing-masing data dengan rata-ratanya.

1. Mencari simpangan baku dari data terserak

Simpangan baku atau deviasi standar populasi yang diberi notasi  (baca sigma) dapat dihitung menggunakan rumus di bawah ini.

 =

N

Y

N

)

Y

(

i 2 i2 ( Y_N) 2 i 













Untuk memahami bagaimana cara mencari simpangan baku populasi coba perhatikan contoh berikut ini. Hasil sensus terhadap 30 ekor biri-biri usia 1 tahun hasil cloning (kembaran) menunjukkan berat sebagai berikut (dalam kg):

79 89 87 69 69 60 62 72 72 72 60 97 66 66 66 79 81 78 88 68 82 84 91 82 98 89 96 82 83 86

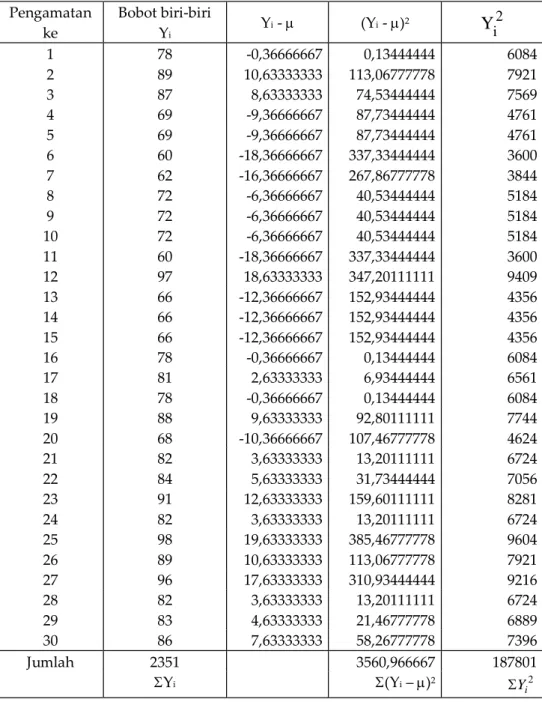
Jika dibuat tabel akan tersaji pada Tabel 5.9. Hasil perhitungannya seperti berikut.

 =

30

0967

,

3560

N

)

Y

(

_i 2









= 10,894 kg atau :  =

30

187801

N

Y

30 ) 2351 ( N ) Y ( 2 i 2 2 i









= 10,895 kg

Untuk mencari simpangan baku atau deviasi standar sampel, diberi notasi s, dapat digunakan rumus di bawah ini.

S =

1

n

n

)

Y

(

Y

1

n

)

Y

Y

(

2 i 2 i 2 i

















Coba perhatikan perhitungan simpangan baku sampel dengan contoh berikut ini. Misalkan ketigapuluh biri-biri tersebut merupakan sampel yang diambil secara acak dari 100 biri-biri hasil cloning yang sudah berhasil dilaksanakan. Dengan demikian, data yang diperoleh merupakan data statistik sampel (lihat Tabel 5.9), sehingga:

1 30 966667 , 3560 1 ) ( 2      n Y Y_i = √ = 11,0811531 atau dihitung dengan rumus yang satunya yaitu:

s

=

Yi

2₋ Yi 2 n

n− s = simpangan baku untuk sampel, pembaginya n-1

Tabel 5.9 Data Sensus Bobot Biri-Biri Hasil Cloning Usia Satu Tahun (dalam kg) Pengamatan ke Bobot biri-biri Yi Y i -  (Yi - )2 2 i

Y

1 78 -0,36666667 0,13444444 6084 2 89 10,63333333 113,06777778 7921 3 87 8,63333333 74,53444444 7569 4 69 -9,36666667 87,73444444 4761 5 69 -9,36666667 87,73444444 4761 6 60 -18,36666667 337,33444444 3600 7 62 -16,36666667 267,86777778 3844 8 72 -6,36666667 40,53444444 5184 9 72 -6,36666667 40,53444444 5184 10 72 -6,36666667 40,53444444 5184 11 60 -18,36666667 337,33444444 3600 12 97 18,63333333 347,20111111 9409 13 66 -12,36666667 152,93444444 4356 14 66 -12,36666667 152,93444444 4356 15 66 -12,36666667 152,93444444 4356 16 78 -0,36666667 0,13444444 6084 17 81 2,63333333 6,93444444 6561 18 78 -0,36666667 0,13444444 6084 19 88 9,63333333 92,80111111 7744 20 68 -10,36666667 107,46777778 4624 21 82 3,63333333 13,20111111 6724 22 84 5,63333333 31,73444444 7056 23 91 12,63333333 159,60111111 8281 24 82 3,63333333 13,20111111 6724 25 98 19,63333333 385,46777778 9604 26 89 10,63333333 113,06777778 7921 27 96 17,63333333 310,93444444 9216 28 82 3,63333333 13,20111111 6724 29 83 4,63333333 21,46777778 6889 30 86 7,63333333 58,26777778 7396 Jumlah 2351 3560,966667 187801 Yi (Yi – )2 2 i Y 

Dengan menggunakan kalkulator fx-350MS atau yang sejenisnya, setelah dinyalakan tombol  tekan 

tekan , di layar kalkulator tampak huruf SD. Data ke-1 bobot biri-biri (Tabel 5.9) 78 lalu tekan tombol data DT (warna biru) untuk yang ini jadi satu dengan tombol .

Setelah memasukkan data 78 tekan tombol , maka di layar muncul n = 1, artinya data yang sudah masuk 1 buah. Data dimasukkan lagi sampai data ke-30 yaitu 86, di layar akan muncul n =30.

= ….? = ….?

tekan  (S-SUM) Di layar akan muncul

tekan 1 muncul angka 187,801 ini artinya = 187801

tekan  muncul angka 2,351 ini artinya ∑Y = 2351 Tekan (S-VAR), di layar akan muncul

tekan muncul angka 78.36666667 ini artinya ̅ = 78,36666667

Angka-angka yang sudah diperoleh dimasukkan ke rumus

s

=

Y_i2− Yi 2 n n−

s

=

− (2 )2 −

= √

− −

= √

=

√ s = 11,0811531  11,08

Sekarang cobalah tekan tombol (dengan lambang xn-1), di layar muncul angka berapakah? Sama dengan yang manakah?

2. Mencari simpangan baku dari data yang dikelompokkan

Jika data sudah dikelompokkan, atau data yang diperoleh berupa data sekunder yang telah dikelompokkan, masih dapat dicari harga simpangan baku atau deviasi standar populasinya dengan rumus seperti berikut.

 =

N

)

Y

(

f

_{i i}





2



Untuk simpangan baku atau deviasi standar sampel (s) dapat dihitung dengan rumus sebagai berikut: s =

1

n

)

Y

Y

(

f

_{i i} 2







Sebagai perhitungannya, coba Anda perhatikan contoh berikut ini. Hasil sensus terhadap seluruh tanaman lamtoro yang tumbuh di pekarangan penduduk desa Jeruk Sawit, yakni sebanyak 60 batang, seperti pada Tabel 5.10.

Rerata populasi () dari N data di atas sebanyak 60 buah yang telah dikelompokkan menjadi 7 kelas adalah:

 =

63,17

dm

60

3790

N

Y

f

_{i i}







 =

60

334

,

17693

N

)

Y

(

f

_{i i} 2









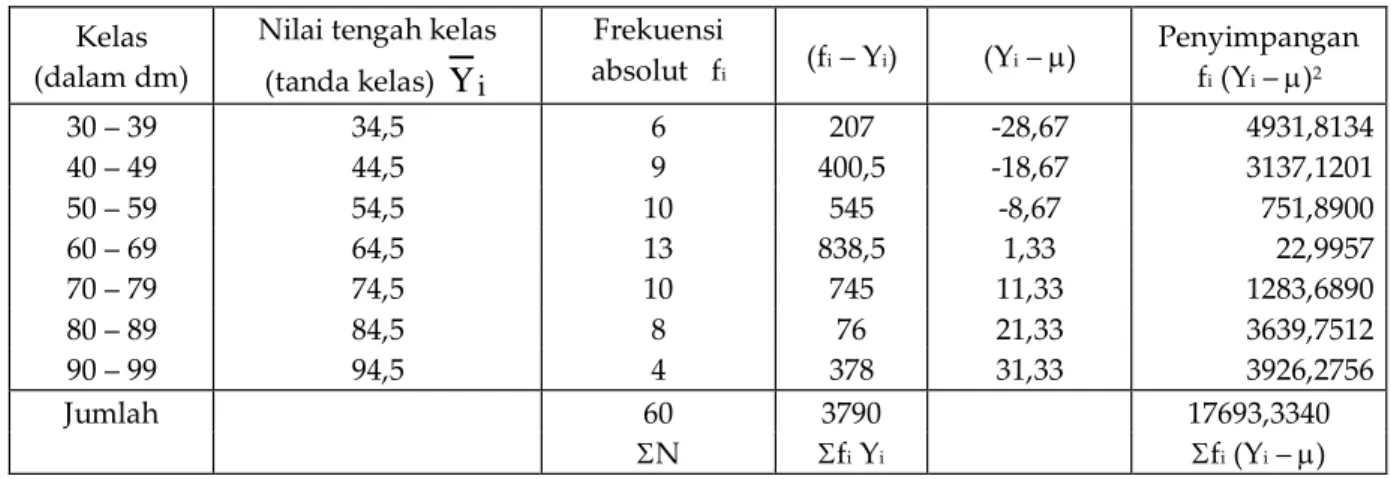
= 17,172 dm ∑x2 ∑x n 1 2 3 𝑥 xn xn-1 1 2 3

Tabel 5.10 Data Sensus Tinggi Tanaman Lamtoro di Pekarangan Penduduk Desa Jeruk Sawit

Kelas (dalam dm)

Nilai tengah kelas (tanda kelas)

Y

i Frekuensi absolut fi (fi – Yi) (Yi – ) Penyimpangan fi (Yi – )2 30 – 39 34,5 6 207 -28,67 4931,8134 40 – 49 44,5 9 400,5 -18,67 3137,1201 50 – 59 54,5 10 545 -8,67 751,8900 60 – 69 64,5 13 838,5 1,33 22,9957 70 – 79 74,5 10 745 11,33 1283,6890 80 – 89 84,5 8 76 21,33 3639,7512 90 – 99 94,5 4 378 31,33 3926,2756 Jumlah 60 3790 17693,3340 N fi Yi fi (Yi – ) Untuk perhitungan penelitian sampling dapat anda perhatikan contoh berikut ini.

Jika data 60 batang lamtoro yang telah diukur diambil secara acak dari 300 pohon yang ada di desa Jeruk Sawit, maka simpangan baku yang diperoleh merupakan simpangan baku sampel, dan perhitungannya adalah seperti berikut. Rerata sampel ( Y ):

Y

= 60 3790   n Y f_{i i} = 63,17 dm s = 1 60 334 , 17693 1 ) ( 2      n Y Y f_{i i} = 17,317 dm

Coba Anda perhatikan besarnya rata-rata dan besarnya simpangan baku antara populasi dan sampel dengan data apakah yang harganya sama? Manakah yang harganya lebih kecil?

D. VARIANSI ATAU RAGAM (variance)

Varians(i) atau ragam (variance) adalah kuadrat dari simpangan baku. Varians atau ragam populasi diberi simbol 2_{. Simpangan baku sampel diberi simbol s. Jika}

besarnya simpangan baku populasi () sudah diketahui yaitu 17,172 maka besarnya varians atau ragam populasi dapat dihitung yaitu sebesar: 2 _{= 17,172}2 _{= 294,877584} 

294,88.

Perhatikan contoh data 30 bobot biri-biri (data Tabel 5.9) dari perhitungan sebelumnya diperoleh s = 11,0811531 maka besarnya variansi atau ragam sampel: s2 _{= (11,0811531)}2

= 122,791954.

E. KOEFISIEN VARIASI/KOEFISIEN VARIABILITAS ATAU ANGKA BAKU

(coeffisien of variability/coeffisien of variation)

Koefisien variansi atau koefisien variabilitas (koefisien keragaman, KK) adalah simpangan baku dibagi dengan rata-ratanya dikalikan 100%. Koefisien variasi diberi simbol CV. Jika besarnya simpangan baku populasi () = 17,172 dan rata-rata populasi () = 63,17, maka besarnya koefisien variasi sampel (CV):

CV (KK, Koefisien Keragaman) populasi

=

 x 100%

CV = 100% 17 , 63 172 , 17 _ = 27,1838%

Perhatikan contoh data 30 bobot biri-biri (data Tabel 5.9) dari perhitungan sebelumnya diperoleh s = 11,0811531 dan ̅

=

78,36666667.

CV bobot biri-biri =

̅ x 100%  =

Koefisien keragaman (KK, CV) dari kelompok data hasil penelitian yang baik adalah berkisar antara 3% sampai dengan 20%. Koefisien keragaman data hasil penelitian tidak diharapkan melebihi 30%, karena variasi datanya terlalu besar. Jika nanti data dengan KK yang besar melebihi 30% digunakan untuk uji beda, hasilnya akan menjadi bias.

F. GALAT BAKU RATA-RATA ATAU SIMPANGAN BAKU RATA-RATA (Simpangan Baku Rerata; STANDARD ERROR)

Galat baku rata-rata (rerata) atau simpangan baku rata-rata (standard error) adalah

simpangan baku dibagi dengan akar banyaknya data, atau akar (varians dibagi banyaknya data). Galat baku rata-rata atau simpangan baku rata-rata populasi diberi simbol _Y. Besarnya dapat dihitung dengan menggunakan rumus:



_Y̅ = 

√

atau



Y̅ =

√

2

Jika besarnya simpangan baku populasi () = 17,172 dan banyaknya data populasi (N) = 60, maka besarnya galat baku rerata populasi:



_Y =

N  = 60 172 , 17 = 2,216895667  2,22

Perhatikan contoh data 30 bobot biri-biri (data Tabel 5.9) dari perhitungan sebelumnya diperoleh s = 11,0811531 dan s2 _{= 122,791954.} Y̅ = √n

atau Y̅ =

√

2 n

Y̅ biri-biri = √

=

2,023132505 atau _Y̅ biri-biri =

√

=

√ = 2,023132505  2,02

G. CI (CONFINDENT INTERVAL)/SELANG KEPERCAYAAN RERATA Rumus CI = ̅  _Y̅

Misalnya rerata data = 41,000 dan standar error 1,200. Banyaknya data n = 10, maka nilai t diperoleh dari tabel t (kumpulan Tabel no. 04), dengan taraf signifikansi ( ) 5% atau taraf kepercayaannya 95%. Cara membaca pada nilai t-tabel ( 2 arah, two tail areas) dicari dulu db (derajat bebas, degree of freedom, degree of variation), yaitu n – 1; 10-1 = 9; maka dengan db = 9 dan

(taraf signifikansi) 5% atau 0,05 diperoleh angka 2,2622. Hasil perhitungan CI adalah:

CI = 41,000  2,2622 x 1,200  41,000  2,71464, dengan demikian selang kepercayaan rerata 95% dari kelompok data tersebut adalah berkisar antara 38,28536—43,71464.

Perhatikan data 30 bobot biri-biri, diperoleh _Y̅ = 2,023132505 dan ̅ = 78,36666667, n = 30, maka db = 30 – 1 = 29, nilai t0,05(db = 29) = 2,0452.

CI = 78,36666667  (2,0452 x 2,023132505)  78,36666667  4,137710599, dengan demikian selang kepercayaan rerata 95% data bobot biri-biri adalah berkisar antara 74,22895607- 82,50437727  74,23 - 82,50.

Untuk memperdalam pemahaman mengenai kegunaan materi statistika deskriptif ukuran dispersi (sebaran), silakan menjawab latihan berikut ini!

1. Jelaskan enam hal yang mampu menjadi ukuran dispersi dari kelompok suatu data? 2. Jelaskan hubungan antara simpangan baku, galat baku dan ragam!

3. Apa artinya bila data memiliki harga simpangan baku yang sangat besar?

D. Ringkasan

Ringkasan yang dapat ditarik setelah Anda mempelajari materi yang ada dalam Kegiatan Belajar variabilitas seperti berikut ini.

1. Untuk menginterpretasikan data, maka data tersebut tidak hanya disajikan dalam bentuk ukuran pemusatan. Agar dapat diinterpretasikan dengan tepat maka diperlukan informasi lain yakni berupa ukuran-ukuran penyimpangan/variabilitas.

2. Setiap ukuran penyimpangan/variabilitas memberikan informasi spesifik, seperti range akan memberikan informasi nilai minimum dan maksimum dari data yang dimiliki; simpangan baku memberikan informasi besarnya standar penyimpangan data dari nilai rata-ratanya; simpangan baku rata-rata menggambarkan besarnya nilai standar kekeliruan dari nilai rata-ratanya, dan seterusnya.

3. Semakin besar nilai penyimpangan/variabilitas dari data yang dimiliki semakin bervariasi/ beragam nilai-nilai dari data tersebut, dan semakin kecil ukuran penyimpangan berarti semakin seragam nilai-nilai data tersebut.

E. Latihan Soal

01. Mengapakah kita memerlukan ukuran gejala pusat dan penyimpangan? 02. Apakah arti median dan apakah kegunaannya?

03. Apakah arti kuartil, desil, persentil? Apakah kegunannya?

04. Mengapakah kita memerlukan simpangan baku, varians, dan standard error? 05. Apakah manfaat angka baku?

06. Apakah yang dimaksud dengan koefisien keragaman? Apakah manfaatnya?

07. Data berikut merupakan data skor hasil lempar cakram mahasiswa Biologi dalam uji kemampuan fisik. 22 25 25 21 29 19 20 26 25 20 26 28 15 16 19 22 25 27 24 25 33 30 28 29 20 18 20 24 25 26 30 28 27 25 25 25 20 18 26 25 24 27 27 28 31

a. Buatlah data di atas ke dalam bentuk distribusi kelompok!

b. Buatlah perhitungan-perhitungan berdasarkan data terserak (tunggal): 1) rerata hitung, geometrik, harmonik! 5) varians (ragam) 2) modus dan median! 6) koefisien keragaman

3) rentang 7) selang kepercayaan rerata (CI) 4) simpangan baku

08. Berikut kumpulkan data dari mahasiswa peserta statistika kelas Saudara tentang: a) umur (dalam bulan); b) massa (bobot) (kg); c) tinggi (m)

d) indeks massa badan: _{( )} ( )

Buatlah perhitungan-perhitungan berdasarkan data terserak/tunggal. 1) rerata hitung, geometrik, harmonik! 5) varians (ragam) 2) modus dan median! 6) koefisien keragaman

3) rentang 7) selang kepercayaan rerata (CI) 4) simpangan baku

Sulisetijono

Biologi FMIPA Universitas Negeri Malang

(State University of Malang)

Email: sulisetijono.fmipa@um.ac.id copyright August 2016