UJI PENDEKATAN NORMAL OSIUS-ROJEK PADA DIAGNOSTIK MODEL REGRESI LOGISTIK

commit to user

UJI PENDEKATAN NORMAL OSIUS-ROJEK PADA

DIAGNOSTIK MODEL REGRESI LOGISTIK

Oleh

ANTO WICAKSONO NIM. M 0105023

SKRIPSI

ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SEBELAS MARET

SKRIPSI

UJI PENDEKATAN NORMAL OSIUS-ROJEK PADA DIAGNOSTIK MODEL REGRESI LOGISTIK

yang disusun oleh

ANTO WICAKSONO

NIM. M0105023

dibimbing oleh

Pembimbing I

Dra. Respatiwulan, M.Si. NIP. 19680611 199302 2 001

Pembimbing II

Sri Kuntari, M.Si. NIP. 19730225 199903 2 001

telah dipertahankan di depan Dewan Penguji

pada hari Selasa, tanggal 4 Agustus 2009

dan dinyatakan telah memenuhi syarat.

Anggota Tim Penguji Tanda Tangan

1. Irwan Susanto, S.Si, DEA

NIP. 19710511 199512 1 001

2. Drs. Muslich, M.Si

NIP. 19521118 197903 1 001

3. Dra. Yuliana Susanti, M.Si

NIP. 19611219 198703 2 001

1. ...

2. ...

3. ...

Disahkan oleh

Fakultas Matematika dan Ilmu Pengetahuan Alam

Dekan Ketua Jurusan Matematika

Prof. Drs. Sutarno, M.Sc., Ph.D.

NIP. 19600809 198612 1 001

Drs. Kartiko, M.Si.

commit to user ABSTRAK

Anto Wicaksono, 2009. UJI PENDEKATAN NORMAL OSIUS-ROJEK PADA DIAGNOSTIK MODEL REGRESI LOGISTIK. Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sebelas Maret.

Model regresi logistik digunakan untuk menunjukkan pola hubungan antara variabel respon yang bersifat kualitatif dan variabel prediktor. Pada model regresi logistik digunakan uji diagnostik model untuk mengevaluasi apakah model sesuai dengan data.

Metode penelitian yang digunakan dalam skripsi ini adalah studi literatur. Tujuan skripsi yaitu menentukan statistik uji pendekatan normal Osius-Rojek dan menerapkan dalam contoh. Estimasi parameter model regresi logistik dilakukan dengan metode maksimum likelihood. Uji signifikansi parameter yang digunakan pada model adalah uji rasio likelihood dan uji chi-kuadrat Wald.

Hasil pembahasan didapatkan statistik uji pendekatan normal Osius-Rojek berdistribusi normal standar untuk ukuran sampel besar. Hasil penerapan uji diagnostik pada contoh mengenai pengaruh dan pengalaman seseorang terhadap status penggunaan mammography (Hosmer and Lemeshow, 1989) didapatkan bahwa model regresi logistik sesuai dengan data.

ABSTRACT

Anto Wicaksono, 2009. THE DIAGNOSTIC OF LOGISTIC REGRESSION MODEL WITH OSIUS-ROJEK NORMAL APPROXIMATION TEST. Mathematics and Natural Science Faculty, Sebelas Maret University.

Logistic regression model is used to explain the relationship between of qualitative response variables and variables predictor. In the logistic regression model, the test diagnostic is used to evaluate whether the model is apropriate to the data.

The research method is literature study. The objective are to determine the statistic test of Osius-Rojek normal approximation test and to apply in an example. The parameter estimation use the maximum likelihood method. The parameter significance test are done by likelihood ratio test and Wald chi-square test.

The result of discussion are the distribution of a statistics test for Osius-Rojek normal approximation test is normal standard for large sample. The application of the test results on the influence and experience of someone of the status of the use of mammography (Hosmer and Lemeshow, 1989) found that the logistic regression model is apropriate to the data.

commit to user MOTO

PERSEMBAHAN

Karya sederhana ini kupersembahkan untuk.

Bapak dan Ibu tercinta, begitu besar pengorbanan dan kasih sayangmu terhadap diriku serta senantiasa berdoa kepada Allah SWT untuk kebaikan anak-anaknya semua itu tak kan terbayarkan sampai kapanpun.

Kakakku Okta, adikku Sari dan Dimas terima kasih untuk motivasi dan dukungannya.

Keluarga besar yang selalu memberi semangat dan mendukung setiap langkahku.

commit to user KATA PENGANTAR

Puji syukur penulis panjatkan kepada Allah SWT yang telah melimpahkan rahmat dan hidayah-Nya sehingga penulis berhasil menyelesaikan skripsi yang berjudul uji pendekatan normal Osius-Rojek pada diagnostik model regresi logistik. Sholawat dan salam semoga senantiasa tercurahkan kepada Nabi Muhammad SAW sebagai pembawa risalah islam.

Pada kesempatan ini penulis mengucapkan terima kasih kepada

1. Dra. Respatiwulan, M.Si sebagai pembimbing I dan Sri Kuntari, M.Si sebagai pembimbing II yang telah banyak memberikan ide, bimbingan, arahan dan kesabaran bagi penulis dalam menyelesaikan skripsi ini.

2. Budi yang telah memberikan masukan dalam penulisan skripsi ini. 3. Semua pihak yang telah membantu kelancaran penulisan skripsi ini.

Penulis berharap semoga saran dan kritik yang membangun untuk perbaikan skripsi ini dan semoga karya sederhana ini dapat bermanfaat bagi semua pembaca.

DAFTAR ISI

halaman

JUDUL ... i

PENGESAHAN ... ii

ABSTRAK...iii

ABSTRACT...iv

MOTO ... v

PERSEMBAHAN...vi

KATA PENGANTAR...vii

DAFTAR ISI...ix

DAFTAR TABEL...x

BAB I PENDAHULUAN...1

1.1 Latar Belakang Masalah ... 1

1.2 Rumusan Masalah ... 2

1.3 Batasan Masalah ... 2

1.4 Tujuan Penulisan ... 2

1.5 Manfaat Penulisan ... 3

BAB II LANDASAN TEORI...4

2.1 Tinjauan Pustaka ... 4

2.1.1 Probabilitas Variabel Random ... 4

2.1.2 Distribusi Sampling...5

2.1.3 Distribusi Bernoulli dan binomial ... 6

2.1.4 Model Regresi Linear ... 7

2.1.5 Regresi Linear Terbobot ... 8

2.1.6 Model Regresi Logistik Biner ... 9

commit to user

2.1.10 Interpretasi Parameter Model...15

2.2 Kerangka Pemikiran...16

BAB III METODE PENELITIAN...17

BAB IV PEMBAHASAN...18

4.1 Prosedur uji pendekatan normal Osius dan Rojek...18

4.2 Contoh...20

BAB V PENUTUP...26

5.1 Kesimpulan...26

5.2 Saran...27

DAFTAR PUSTAKA...28

LAMPIRAN 1...29

LAMPIRAN 2...32

LAMPIRAN 3...38

LAMPIRAN 4...39

DAFTAR TABEL

4.2.1 Sikap wanita terhadap status penggunaan mammography...20

4.2.2. Estimasi Parameter 5 Variabel Prediktor...21

4.2.3 Uji Rasio Likelihood 5 Variabel Prediktor...21

4.2.4 Estimasi parameter 3 Variabel Prediktor...22

4.2.5 Uji rasio likelihood 3 Variabel Prediktor...23

4.2.6. Hasil perhitungan nilai ˆπ_j,v_j, dan c_j...23

4.2.7 Anova……...23

commit to user

BAB I

PENDAHULUAN

1. Latar Belakang Masalah

Pada bidang ilmu kesehatan, banyak peneliti ingin mempelajari hubungan

antara 2 variabel atau lebih. Misalnya, hubungan antara tekanan darah dan umur,

konsentrasi obat dan kecepatan detak jantung (Daniel,1995). Oleh karena itu

diperlukan metode untuk menunjukkan hubungan antara variabel-variabel tersebut.

Menurut Soejoeti (1986) metode yang digunakan untuk menunjukkan hubungan antar

2 variabel atau lebih adalah model regresi.

Model regresi memiliki variabel prediktor dan variabel respon. Variabel

prediktor dan variabel respon dapat bertipe data kuantitatif atau kualitatif. Menurut

Hosmer dan Lemeshow (1989) model regresi yang sesuai bila variabel respon bersifat

kualitatif adalah model regresi logistik. Model regresi logistik dengan nilai variabel

respon terdiri dari 2 kategori disebut model regresi logistik biner sedangkan model

regresi logistik dengan nilai variabel respon lebih dari 2 kategori disebut model

regresi logistik polytomous.

Model regresi logistik memuat parameter yang harus diestimasi. Menurut

Neter et al (1996) estimasi parameter model regresi logistik didapatkan melalui

metode maksimum likelihood. Hasil estimasi parameter perlu uji signifikansi

terhadap model. Menurut Hosmer dan Lemeshow (1989) uji signifikansi parameter

yang digunakan pada model regresi logistik adalah uji rasio likelihood dan uji

chi-kuadrat Wald.

Setelah estimasi dan uji signifikansi parameter model, perlu dilakukan uji

diagnostik model untuk mengevaluasi apakah model regresi logistik sesuai dengan

data (Hosmer and Lemeshow, 1989). Menurut Liu (2007) salah satu uji diagnostik

model regresi logistik adalah uji chi-kuadrat Pearson yang didasarkan pada pola

kovariat. Pola kovariat adalah kelompok nilai yang sama dari masing-masing variabel

Selain uji chi-kuadrat Pearson terdapat uji diagnostik lain yang didasarkan

pada pola kovariat yaitu uji pendekatan normal Osius-Rojek (Liu,2007). Statistik uji

pendekatan normal Osius-Rojek merupakan pengembangan statistik uji chi-kuadrat

Pearson. Statistik uji pendekatan normal Osius-Rojek berdistribusi normal standar

untuk ukuran sampel besar. Pada penulisan skripsi ini dilakukan uji diagnostik model

melalui uji pendekatan normal Osius-Rojek dan menerapkan uji pada pengaruh dan

pengalaman seseorang terhadap status penggunaan mammography (Hosmer and

Lemeshow, 1989) melalui uji pendekatan normal Osius-Rojek.

2. Rumusan Masalah

Masalah yang dibahas dalam skripsi adalah

1. Bagaimana menentukan statistik uji pendekatan normal Osius-Rojek pada

model regresi logistik.

2. Bagaimana menerapkan uji pendekatan normal Osius-Rojek pada pengaruh

dan pengalaman seseorang terhadap status penggunaan mammography.

3. Batasan Masalah

Penulisan skripsi dibatasi pada kasus model regresi logistik biner dan metode

yang digunakan untuk mengestimasi parameter model adalah metode maksimum

likelihood.

4. Tujuan Penulisan

Tujuan dari penulisan skripsi ini adalah

1. Menentukan statistik uji pendekatan normal Osius-Rojek pada model regresi

logistik.

2. Menerapkan uji pendekatan normal Osius-Rojek pada pengaruh dan

commit to user

5 . Manfaat Penulisan

Manfaat yang diperoleh dari penulisan skripsi adalah memperluas wawasan

mengenai uji diagnostik model melalui uji pendekatan Osius-Rojek sebagai suatu

BAB II

LANDASAN TEORI

2.1 Tinjauan Pustaka

Pada tinjauan pustaka diberikan hal-hal yang mendasari penulisan skripsi ini,

yaitu berupa konsep dan teori yang berkaitan dengan diagnostik model regresi

logistik. Teori yang berkaitan meliputi probabilitas variabel random, distribusi

sampling, distribusi Bernoulli dan binomial, model regresi linear, regresi linear

terbobot, model regresi logistik biner, estimasi maksimum likelihood, uji chi-kuadrat

Pearson,interpretasi model regresi logistik.

2.1.1 Probabilitas Variabel Random

Berikut ini definisi-definisi yang berkaitan dengan variabel random menurut

Bain dan Engelhardt (1992).

Definisi 2.1.1

Suatu variabel random X adalah suatu fungsi bernilai real R dengan domain ruang

sampel S, untuk setiap ZS dan suatu bilangan real x atau x\ , sedemikian

sehinggaX Z x.

Berikut ini diberikan definisi mengenai variabel random diskrit dan variabel

random kontinu.

Definisi 2.1.2

Variabel random X dikatakan variabel random diskrit jika himpunan semua nilai

yang mungkin dari variabel random X adalah himpunan yang terhitung yaitu

!

1, 2, , n

commit to user

Definisi 2.1.3

Variabel random X dikatakan variabel random kontinu jika terdapat fungsi densitas

probabilitas f x( ) sehingga fungsi distribusi kumulatif dapat dinyatakan sebagai

( ) _{( )}

x

F x f t dt d

=

¨

.

Definisi 2.1.4. Diberikan X suatu variabel random kontinu dengan fungsi densitas

probabilitas f x . Harga harapan dari X dinyatakan dengan

( ) ( ) .

E X fxf x dx f

³

Selanjutnya diberikan definisi tentang fungsi pembangkit momen yang

diambil dari Bain dan Engelhardt (1992).

Definisi 2.1.5. Diberikan X suatu variabel random, fungsi pembangkit momen (fpm)

dinyatakan dengan

.

tX X

M t E e

Harga harapan dari X atau E X didapatkan melalui momen pertama dari fpm yaitu

2.1.2 Distribusi Sampling

Distribusi sampling adalah distribusi dari suatu statistik. Berikut ini diberikan

teorema-teorema yang berkaitan dengan distribusi sampling menurut Bain dan

Engelhardt (1992).

Teorema 2.1.1.JikaX₁,!,X_nadalah variabel random dari suatu distribusi dengan rata-rata P dan variansi V2

P

S adalah independen

dengan ( ) F ( )

2.1.3 Distribusi Bernoulli dan Binomial

Menurut Bain dan Engelhardt (1992), variabel random yang menyatakan 2

kemungkinan kejadian yaitu sukses atau gagal disebut variabel Bernoulli dan

dinyatakan dengan

1 , jika kejadian sukses

0 , jika kejadian gagal

e

Jika a adalah probabilitas sukses dan b adalah probabilitas gagal maka fungsi

densitas probabilitas untuk distribusi Bernoulli didefinisikan sebagai

1 _{, 0,1}

x x

commit to user

Distribusi binomial merupakan ulangan n kali percobaan Bernoulli dengan

variabel random X menyatakan banyak kejadian sukses. Probabilitas banyaknya

peristiwa sukses dari suatu distribusi probabilitas binomial dirumuskan sebagai

, 0,1, ,

dengan x adalah banyaknya peristiwa sukses, n adalah banyaknya percobaan yang

dilakukan. Variabel random X dengan distribusi binomial memiliki E X nadan

var X nab.

2.1.4 Model Regresi Linear

Menurut Neter et al. (1996) model regresi yang memiliki satu variabel

prediktorX disebut model regresi linear sederhana dan dimodelkan sebagai

0 1 , 1, 2, ,

i i i

Y E E X H i ! n (2.1)

dengan Y_i: variabel respon percobaan ke-i,

i

X : variabel prediktor percobaan ke-i,

0, 1

E E merupakan parameter regresi,

i

H merupakan galat random dan H_i ~N

0,V2

.

Model regresi yang memiliki lebih dari satu variabel prediktor disebut model

regresi linear ganda. Jika X X₁, ₂,!,X_p adalah variabel prediktor dengan n

pengamatan dan Y adalah variabel respon maka model regresi linear ganda dapat

dinyatakan sebagai

0 1 1 2 2 p p

Y E E X E X " E X H,

dan untuk pengamatan ke-idapat dituliskan

0 1 1 2 2 , 1, 2, ,

i i i p i p i

2.1.5 Regresi Linear Terbobot

Model regresi linear dengan variansi galat tidak konstan dapat diestimasi

menggunakan metode kuadrat terkecil terbobot. Menurut Neter dan Wasserman

(1996) metode kuadrat bobot terkecil untuk satu variabel prediktor dinyatakan dengan

2

dengan w_i adalah pembobot. Estimasi parameter regresi didapatkan dengan

meminimumkan S

E E₀, ₁

yaitu menurunkan S

E E₀, ₁

terhadap masing-masing

w sehingga didapatkan persamaan

0 1

Estimasi parameter regresi didapatkan dengan menyelesaikan persamaan (2.3) yang

commit to user

2.1.6 Model Regresi Logistik Biner

Menurut Hosmer dan Lemeshow (1989) model regresi logistik adalah model

yang menyatakan pola hubungan antara variabel prediktor dan variabel respon yang

bersifat kualitatif. Model regresi logistik sederhana yaitu model regresi logistik yang

memiliki satu variabel prediktor X sedangkan model regresi logistik yang memiliki

lebih dari satu variabel prediktor X disebut model regresi logistik ganda. Misalkan

nilai variabel y 1 menyatakan adanya suatu karakteristik dengan probabilitas S x

dan y 0 menyatakan tidak adanya suatu karakteristik dengan probabilitas 1S x

sehingga E y

1|X

S x adalah harga harapan dari y 1 untuk setiap harga x dan

0 |

1

E y X S x dan nilai S(x) terletak pada interval [0,1]. Misalkan terdapat p

variabel prediktor sehingga model regresi logistik dapat dinyatakan sebagai harga

harapan dari Y untuk setiap harga x yang diberikan, dinyatakan sebagai

0 1 1 0 1

denganE_h menyatakan parameter-parameter regresi ke-h,X_hadalah pengamatan

variabel prediktor ke-h untuk h 1, 2!,p

Pada model regresi logistik dilakukan transformasi untuk melinearkan

variabel prediktor terhadap fungsi respon. Transformasi yang digunakan pada model

(2.4) adalah transformasi logit yang dinyatakan dengan g x . Tranformasi logit

didapatkan melalui perbandingan dari S x terhadap 1S x yaitu

( 0 1 1 ... )

sehingga persamaan (2.4) menjadi

exp( ( ))

Apabila variabel prediktor bersifat kualitatif, menurut Draper and Smith

(1998) variabel rancangan diperlukan untuk menunjukkan nilai dari variabel prediktor

dalam model. Jika sebuah variabel berskala kualitatif mempunyai k kategori, maka

dibutuhkan k1 variabel rancangan (Hosmer and Lemeshow, 1989). Misalkan

variabel prediktor ke-h = xh berskala kualitatif dengan k kategori, digunakan k1

variabel rancangan dalam model. Jika variabel-variabel rancangan tersebut

dinyatakan dengan xh(u) dan koefisien-koefisiennya dinyatakan dengan ȕhu, dengan

u=1,2,..., k-1 maka bentuk logit untuk model dengan p variabel prediktor adalah

2.1.7 Estimasi Maksimum Likelihood

Menurut Hosmer dan Lemeshow (1989) estimasi parameter yang digunakan

dalam model regresi logistik adalah metode maksimum likelihood. Berikut ini

diberikan definisi yang diacu dari Bain dan Engelhardt (1992).

Definisi 2.1.6 Fungsi densitas probabilitas bersama dari n variabel random

1, 2, , n

commit to user

estimasi maksimum likelihood dari T yang memenuhi

1, 2, , n;ˆ

max

1, 2, , n;

Setiap variabel respon Y_i untuk model regresi logistik adalah variabel random

berdistribusi Bernoulli dengan probabilitas sukses S x_i dan X_i adalah variabel

prediktor yang bersesuaian dengan Y_i dengan i 1, 2,!,n. Menurut Hosmer dan

Lameshow (1989), fungsi likelihood distribusi Bernoulli untuk n sampel independen

adalah

Menurut Bain dan Engelhart (1992) memaksimumkan fungsi likelihood sama

dengan memaksimumkan fungsi log-likelihood. Fungsi log-likelihood dinyatakan

dengan lnL E sehingga persamaan (2.6) menjadi

estimasi maksimum likelihood didapatkan dengan mencari nilai ˆE yang

menurunkan fungsi log-likelihood terhadap parameter E_h dan ( ) 0

umum turunan pertama dari A E terhadap masing-masing parameter adalah

Pandang kembali persamaan (2.4) sehingga y_i S x_i menjadi

0

Estimasi parameter E₀ didapatkan dengan menyelesaikan persamaan (2.9) yaitu

0

diperoleh dan akan ditentukan kemudian. Hal ini menunjukkan bahwa turunan

pertama fungsi likelihood tidak memberikan penyelesaian estimasi parameter regresi.

Menurut Agresti (1984) estimasi parameter E₀,!,E_p dari fungsi likelihood yang

commit to user

Algoritma iterasi Newton-Raphson dipakai oleh software SPSS version 16 dalam

menentukan estimasi paremeter regresi.

2.1.8 Uji Signifikansi Parameter

Uji signifikansi parameter digunakan untuk mengevaluasi apakah variabel

prediktor berpengaruh terhadap variabel respon. Statistik uji yang digunakan untuk

menilai signifikansi parameter model regresi logistik didasarkan pada uji rasio

likelihood(Hosmer and Lemeshow ,1989).

Menurut Hosmer dan Lemeshow (1989) statistik uji rasio likelihood G

didefinisikan sebagai

0 1

2

G L L

dengan L₀ adalah fungsi log-likelihood dari model tanpa variabel prediktor,

sedangkan L₁ adalah fungsi log-likelihood dari model dengan p variabel prediktor.

Uji signifikansi parameter dilakukan dengan membandingkan statistik uji G dengan

2 ( , )Dp

F untuk tingkat signifikansi D dan derajat bebas p (jumlah variabel prediktor).

Jika G!F_{( , )}2_Dp maka H₀ ditolak pada signfikansi D . Uji hipotesis H₀ menyatakan

bahwa tidak ada variabel prediktor yang berpengaruh terhadap respon dan H₁

menyatakan bahwa terdapat paling tidak satu variabel prediktor yang berpengaruh

terhadap respon.

Jika H₀ ditolak maka dilakukan uji lanjut untuk mengevaluasi pengaruh

masing-masing variabel prediktor terhadap variabel respon. Menurut Agresti (1984)

uji signifikansi setiap variabel prediktor dalam model dapat dilakukan menggunakan

uji chi-kuadrat Wald. Menurut Hosmer dan Lemeshow (1989) statisik uji chi-kuadrat

Wald didefinisikan sebagai

dengan hipotesis

0: h 0, 1, 2, ,

H E h ! p (variabel prediktor ke-h tidak berpengaruh terhadap

variabel respon)

1: h 0

H E z (variabel prediktor ke-h berpengaruh terhadap variabel respon)

Jika W !F2_1,D maka H₀ ditolak yang berarti variabel prediktor ke-hberpengaruh

terhadap variabel respon.

2.1.9 Uji Chi-kuadrat Pearson

Pada analisis model regresi logistik digunakan uji diagnostik model untuk

mengevaluasi kesesuaian model dengan data. Menurut Liu (2007) salah satu uji

diagnostik model regresi logistik adalah uji chi-kuadrat Pearson yang didasarkan pada

pola kovariat. Pola kovariat adalah kelompok nilai untuk kovariat yang sama.

Menurut Liu (2007) pola kovariat dibagi menjadi 2 tipe pola yaitu tipe pola pertama

dan tipe pola kedua. Tipe pola pertama menunjukkan bahwa jumlah pola kovariat J

sama dengan ukuran sampel

J n

sedangkan tipe pola kedua menunjukkan bahwa

jumlah pola kovariat J lebih kecil dari ukuran sampel

J n

.

Menurut Hosmer dan Lemeshow (1989) statistik uji chi kuadrat Pearson

didefinisikan sebagai

2

dengan y_j adalah jumlah kejadian sukses pada pola kovariat ke-j, m_j adalah jumlah

subyek pada pola kovariat ke-j, ˆS_j adalah estimasi probabilitas sukses untuk pola

kovariat ke-j, dan v_j adalah variansi jumlah kejadian sukses untuk pola kovariat ke-j.

Menurut Liu (2007) statistik uji chi-kuadrat Pearson berdistribusi chi-kuadrat dengan

commit to user

kritis menunjukkan bahwa H₀ ditolak jika X2 !F_{D,J p 1}. Uji hipotesis H₀

menyatakan bahwa model sesuai dengan data dan H₁ menyatakan bahwa model tidak

sesuai dengan data.

2.1.10 Interpretasi Parameter Model

Interpretasi model dalam model regresi logistik menggunakan rasio odds

(Hosmer dan Lemeshow, 1989). Odds adalah rasio probabilitas kejadian sukses

terhadap probabilitas kejadian gagal. Misalkan variabel prediktor X dikategorikan 0

dan 1 sehingga odds dari variabel respon dengan kategori x 1 dinyatakan dengan

1 /1 1

S S . Odds dari variabel respon dengan kategori x 0 dinyatakan dengan

0 /1 0

S S .

Menurut Hosmer dan Lemeshow (1989) rasio odds merupakan perbandingan

nilai odds untuk kategori x 1 terhadap odds untuk kategori x 0dan didefinisikan

sebagai

Variabel prediktor X untuk kategori 1 akan memberikan nilai \ kali

dibanding variabel prediktor X pada kategori 0 dalam menghasilkan kejadian sukses Y

. Apabila variabel prediktor X bertipe data kuantitatif, interpretasi untuk setiap

2.2 Kerangka Pemikiran

Model regresi logistik digunakan ketika variabel respon bersifat kualitatif.

Model regresi logistik didapatkan melalui estimasi parameter menggunakan metode

maksimum likelihood. Kemudian diuji signifikansi parameter dengan menggunakan

uji rasio likelihood dan uji chi-kuadrat Wald. Setelah estimasi dan uji signifikansi

parameter model, perlu dilakukan uji diagnostik model untuk mengevaluasi apakah

model regresi logistik sesuai dengan data.

Pada sampel besar uji diagnostik yang digunakan pada model adalah uji

pendekatan normal Osius-Rojek Statistik uji pendekatan normal Osius-Rojek

merupakan pengembangan statistik uji chi-kuadrat Pearson. Statistik uji pendekatan

normal Osius-Rojek didapatkan dengan menghitung harga harapan dari statistik uji

chi-kuadrat Pearson dan mengestimasi variansi galat model melalui regresi linier

terbobot. Hasil perhitungan statistik uji digunakan untuk mengevaluasi apakah model

sesuai dengan data. Apabila model sesuai dengan data, maka model dapat

commit to user

BAB III

METODE PENELITIAN

Metode yang digunakan dalam penulisan skripsi ini adalah studi literatur yaitu

melakukan studi ulang mengenai uji diagnostik model regresi logistik melalui uji

pendekatan normal Osius-Rojek.

Langkah-langkah yang ditempuh untuk menguji diagnostik model regresi

logistik dengan uji pendekatan normal Osius-Rojek sebagai berikut

1. Menentukan statistik uji pendekatan normal Osius-Rojek pada model regresi

logistik.

2. Menerapkan model regresi logistik pada data penelitian Zapka dan Spotts dari

Divisi Kesehatan Universitas Massachusetts (Hosmer dan Lemeshow, 1989).

3. Estimasi parameter model menggunakan metode maksimum likelihood.

4. Uji signifikansi parameter menggunakan uji rasio likelihood dan chi-kuadrat

Wald.

5. Uji diagnostik model menggunakan uji pendekatan normal Osius-Rojek.

BAB IV

PEMBAHASAN

Uji diagnostik model digunakan untuk mengetahui kesesuaian model dengan

data. Menurut Hosmer dan Lemeshow (1989) salah satu uji diagnostik model regresi

logistik adalah uji chi kuadrat Pearson. Pada kasus tipe pola pertama yaitu jumlah

pola kovariat J sama dengan ukuran sampel

J n

, statistik uji chi-kuadrat Pearson

tidak berdistribusi chi-kuadrat sehingga statistik uji chi-kuadrat Pearson tidak dapat

digunakan sebagai uji kecocokan model (Liu, 2007). Oleh karena itu digunakan uji

pendekatan normal Osius-Rojek yang dapat diaplikasikan pada kasus J n dan Jn

(Liu, 2007). Statistik uji pendekatan normal Osius-Rojek merupakan pengembangan

dari statistik uji chi-kuadrat Pearson untuk ukuran sampel besar (Liu, 2007).

4.1 Prosedur Uji Pendekatan Normal Osius-Rojek

Uji pendekatan normal Osius-Rojek merupakan uji diagnostik model yang

didasarkan pada pola kovariat. Tahapan uji pendekatan normal Osius-Rojek adalah

menghitung nilai Sˆj,j 1,2,3,",J dengan ˆSj merupakan estimasi probabilitas pola

kovariat ke-j. Kemudian dihitung variansi jumlah sukses untuk setiap pola kovariat

sebesar v_j m_jSˆ_j(1Sˆ_j) untuk 1, 2, 3,j ",J dengan m_j adalah banyak sampel

pada pola kovariat ke-j.

Model regresi logistik menghasilkan variansi galat yang tidak konstan (Neter

and Wasserman, 1974). Pada kondisi variansi galat tidak konstan digunakan metode

kuadrat terkecil terbobot untuk mendapatkan estimasi variansi galat. Menurut Hosmer

dan Lemeshow (1989) tahapan prosedur uji pendekatan normal Osius-Rojek

selanjutnya adalah melakukan regresi linier terbobot untuk variabel respon c_j

terhadap kovariat Xj dengan pembobot vj. Variabel cjdidefinisikan

commit to user

perhitungan Jumlah Kuadrat Galat (JKG) dari regresi linier terbobot tersebut. JKG

merupakan jumlah kuadrat dari nilai estimasi dengan nilai pengamatan sebenarnya.

Menurut McCullagh dan Nelder (1989) jika nilai m_jSˆ_j lebih dari 1 untuk setiap pola

kovariat ke-j maka diberikan faktor koreksi untuk variansi galat

sebesar

Menurut Hosmer dan Lemeshow (1989) statistik uji pendekatan normal

Osius-Rojek didefinisikan sebagai

Liu (2007) menyebutkan bahwa statistik uji z berdistribusi normal standar atau

~ 0,1

z N untuk ukuran sampel besar. Harga harapan dari statistik uji chi-kuadrat

Pearson didapatkan melalui momen pertama dari fungsi pembangkit momen statistik

uji _X2 _yaitu

Pada persamaan (4.1.1) dicari momen ke-1 dan dievaluasi pada t =0 sehingga

didapatkan

Estimasi variansi dari statistik uji chi-kuadrat pearson didapatkan dari nilai

JKG hasil regresi linear terbobot . Menurut Liu (2007) faktor koreksi A sama dengan

0 atau

A 0

bila jumlah pola kovariat J sama dengan jumlah ukuran sampel

J n

.

Hasil perhitungan statistik uji pendekatan normal Osius-Rojek digunakan

untuk mengevaluasi apakah model sesuai dengan data. Daerah kritis menunjukkan

D . Uji hipotesis H₀ menyatakan model sesuai dengan data dan H₁ menyatakan

model tidak sesuai dengan data.

4.2 Contoh

Data yang digunakan untuk menerapkan uji pendekatan normal Osius-Rojek

adalah data penelitian Zapka dan Spotts dari Divisi Kesehatan Universitas

Massachusetts (Hosmer dan Lemeshow, 1989). Data penelitian digunakan untuk

menjelaskan pengaruh pendapat dan pengalaman seseorang terhadap status

penggunaan mammography. Nilai variabel prediktor dan variabel respon diberikan

pada Tabel 4.2.1.

Tabel 4.2.1 Sikap Wanita Terhadap Status Penggunaan Mammography

Pertanyaan Jawaban

Pernah melakukan percobaan mammography?

Variabel Respon Y

0 : Tidak pernah, 1 : Pernah

Tidak membutuhkan mammographykecuali

punya gejala? SYMPT

_{( )}

X₁

1 : Sangat Setuju, 3 : Tidak Setuju 2 : Setuju, 4 : Sangat Tidak Setuju

Merasakan manfaat mammography? PB X₂ Skor persepsi 5 – 20

Riwayat kanker payudara? HIST X₃ 0 : Tidak, 1 : Ya

Periksa payudara sendiri? BSE X₄ 0 : Tidak, 1 : Ya

Mungkinkahmammographytemukan kanker

baru ? DETC

_{( )}

X₅

1 : Tidak Mungkin

2 : Mungkin, 3 : Sangat Mungkin

Nilai variabel PB X₂ pada Tabel 4.2.1 menunjukkan semakin tinggi nilai

skor persepsi semakin menurunkan pendapat orang terhadap manfaat penggunaan

mammography. Hasil estimasi parameter model dengan bantuan program SPSS

version 16 ditunjukkan pada Tabel 4.2.2 sehingga didapatkan estimasi model regresi

commit to user

dengan

11 12 13 2 3

4 51 52

ˆ 3.050 1.704 1.869 0.450 0.185 1.225 1.164 0.168 0.556

g X X X X X

X X X

x

Tabel 4.2.2. Estimasi Parameter 5 Variabel Prediktor

Variabel Db Estimasi

Parameter SE Wald p-value

Konstan 1 3.050 0.572 28.426 0.000

Kemudian dilakukan uji signifikansi parameter dengan menggunakan uji rasio

likelihood. Pada Tabel 4.2.3 yang selengkapnya dapat dilihat pada Lampiran 2

didapatkan nilai uji rasio likelihood.

Tabel 4.2.3 Uji Rasio Likelihood5 Variabel Prediktor

Model

-2 Log

Likelihood G db

Konstanta 563.518

98.517 8

1, 2, 3, 4, 5

X X X X X _465.001

Tabel 4.2.3 menunjukkan nilai 2

(0.05,8)

98.517 15.51

G !F maka H₀ ditolak,

berarti terdapat pengaruh sekurang-kurangnya satu variabel prediktor terhadap

variabel respon atau terdapat pengaruh sikap wanita terhadap status penggunaan

Selanjutnya dilakukan uji chi-kuadrat Wald untuk mengetahui variabel

prediktor yang berpengaruh terhadap variabel respon. Nilai uji chi-kuadrat Wald dari

masing-masing variabel prediktor ditunjukkan pada Tabel 4.2.2. Daerah kritis

menunjukkan bahwa H₀ ditolak jika statistik uji chi-kuadrat Wald > X2(1;0.05) = 3,84

pada tingkat signifikansi D 0.05.

Pada Tabel 4.2.2 didapat nilai statistik uji chi-kuadrat Wald dari seluruh

variabel prediktor dan konstanta yang lebih besar dari F2_0.05,1 3.84 kecuali variabel

X13 dan X51 yang memiliki nilai statistik uji chi-kuadrat Wald lebih kecil dari

20.05,1 3.84

F . Hasil uji signifikansi parameter didapatkan bahwa variabel SYMPT(3)

[X13] dan DETC(1) [X51] tidak berpengaruh signifikan terhadap model regresi logistik

sehingga variabel SYMPT dan DETC (Hosmer dan Lemeshow, 1989).

Selanjutnya estimasi parameter model regresi logistik untuk 3 variabel

prediktor yaitu PB [X2], HIST [X3], BSE [X4] dilakukan melalui estimasi parameter

dengan bantuan program SPSS version 16. Hasil estimasi parameter ditunjukkan

pada Tabel 4.2.4 sehingga diperoleh estimasi model regresi logistik

ˆ

dengan fungsi logit sebagai berkut

2 3 4

ˆ 2.816 0.265X 1.103X 1.179X

g x

Tabel 4.2.4 Estimasi Parameter 3 Variabel Prediktor

Variabel db Estimasi

Parameter SE Wald

KONSTAN 1 2.816 0.529 _28.381

PB [X2] 1 -0.265 0.55 23.455

HIST [X3] 1 -1.103 0.357 9.554

commit to user

Tabel 4.2.5 Uji Rasio Likelihood3 Variabel Prediktor

Model -2 Log Likelihood G db

Konstanta 563.518 53.975 3

Variabel X2, X3, X4 509.543

Tabel 4.2.5 menunjukkan nilai 2

(0.05,3)

98.517!F 7.81

G maka H₀ ditolak,

berarti terdapat pengaruh sekurang-kurangnya satu variabel prediktor terhadap

variabel respon atau terdapat pengaruh sikap wanita terhadap status penggunaan

mammography. Selanjutnya dilakukan uji signifikansi parameter satu-satu dengan

menggunakan uji chi-kuadrat Wald. Pada Tabel 4.2.4 didapatkan nilai statistik uji

chi-kuadrat Wald dari seluruh variabel prediktor dan konstanta yang lebih besar dari

20.05,1 3.84

F sehingga H₀ ditolak, berarti masing-masing variabel prediktor sikap

wanita secara signifikan berpengaruh terhadap status penggunaan mammography.

Tabel 4.2.4 dan Tabel 4.2.5 selengkapnya dapat dilihat pada Lampiran 2.

Setelah didapatkan model regresi logistik yang signifikan dalam parameternya

dilakukan uji diagnostik model melalui uji pendekatan normal Osius-Rojek untuk

mengevaluasi apakah model sesuai dengan data. Prosedur uji pendekatan normal

Osius-Rojek yaitu menghitung nilai ˆS_j,v_j, dan c_j yang disajikan pada Tabel 4.2.6.

Tabel 4.2.7. Anova

Model Jumlah _{Kuadrat db Rataan kuadrat F}

Regresi _{1166.932 3 388.977 6.268}

Galat _{1551.423 25 62.057}

Tabel 4.2.6 selengkapnya dapat dilihat pada Lampiran 3 dan Tabel 4.2.7

selengkapnya dapat dilihat pada Lampiran 4. Pada Tabel 4.2.7 didapatkan nilai JKG

sebesar 1551.423. Berdasarkan pada Tabel 4.2.6 dihitung statistik uji chi-kuadrat

Pearson

2 =2 29-9.251 =39.497. J

j j

A ª_«J m º_»

¬

¦

¼ Nilai statistik uji pendekatan normal

Osius-rojek adalah 15.337

29 3 1

0.242.

regresi logistik sesuai dengan data.

Setelah diketahui bahwa parameter regresi logistik memiliki pengaruh yang

signifikan terhadap estimasi model regresi logistik dan model sesuai dengan data,

selanjutnya dilakukan interpretasi model regresi logistik dengan menggunakan odds

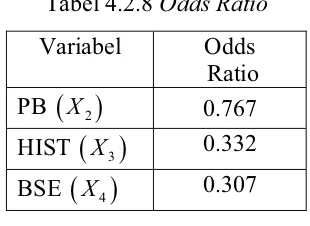
ratio. Pada Tabel 4.2.8 ditunjukkan nilai odds ratio untuk model regresi logistik biner

yang mengandung 3 variabel prediktor. Tabel 4.2.8 selengkapnya dapat dilihat pada

lampiran 2.

Tabel 4.2.8 Odds Ratio

commit to user

penggunaan mammography sebesar 0.767 kali. Proporsi wanita yang mempunyai

riwayat kanker payudara ternyata pernah memeriksakan payudaranya dengan

mammography sebanyak 0.332 kali lebih besar dibandingkan wanita yang tidak

mempunyai riwayat kanker payudara. Proporsi wanita yang dapat memeriksa

payudara sendiri ternyata pernah memeriksakan payudaranya dengan mammography

sebanyak 0.307 kali lebih besar dibandingkan wanita yang tidak dapat memeriksa

BAB V

PENUTUP

5.1. Kesimpulan

Berdasarkan hasil pembahasan, diperoleh kesimpulan sebagai berikut :

1. Uji pendekatan Osius-Rojek merupakan uji diagnostik model regresi logistik

untuk ukuran sampel besar. Statistik uji pendekatan Osius-Rojek adalah

2. Pada pengaruh dan pengalaman seseorang terhadap status penggunaan

mammographydidapatkan estimasi model regresi logistik yang sesuai adalah

ˆ

berarti H₀ diterima sehingga model regresi logistik sesuai dengan data.

3. Berdasarkan nilai odds ratio disimpulkan setiap kenaikan 1 skor persepsi manfaat

penggunaanmammography menunjukkan penurunan penggunaan mammography

sebesar 0.767 kali. Proporsi wanita yang mempunyai riwayat kanker payudara

pernah memeriksakan payudaranya dengan mammography sebanyak 0.332 kali

lebih besar dibandingkan wanita yang tidak mempunyai riwayat kanker payudara.

Proporsi wanita yang dapat memeriksa payudara sendiri ternyata pernah

memeriksakan payudaranya dengan mammography sebanyak 0.307 kali lebih

commit to user

5.2. Saran

Saran yang dapat penulis sampaikan adalah peggunaan uji pendekatan normal

Osius-Rojek pada penulisan skripsi ini dibatasi pada kasus model regresi logistik

biner. Hal ini dimungkinkan untuk membahas uji pendekatan normal Osius-Rojek