STATISTICS
WEEK 6
DISTRIBUSI NORMAL
Pengantar:
Setelah mempelajari materi pokok bahasan disini, mahasiswa diharapkan:
1. Mampu menggunakan konsep0konsep dasar teori Distribusi Probabilitas Kontinu secara benar.
2. Mampu melakukan operasi hitungan0hitungan yang berkaitan dengan
Daftar Isi Materi:
Distribusi Normal
Distribusi Normal Baku Distribusi Normal Baku
Perhatikan grafik Histogram dan
Poligon berikut
Histogram Poligon Kurva f(X)
! """#
$%%& ' ( )
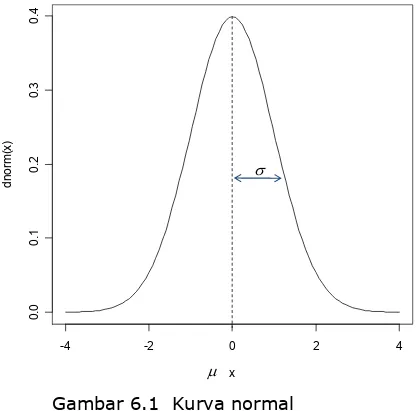
!*+ σ&
( ! ,&
#
-.
Distribusi Normal
Distribusi normal merupakan salah satu distribusi yang paling penting dalam statistika. Disebut pula dengan distribusi Gauss
(Gaussian distribution).
Fungsi densitas dari variabel random X dengan mean dan
Fungsi densitas dari variabel random X dengan mean dan
variansi σ2 adalah:
, −∞ < x <∞
(
)
[ σ ]σ
π
/
,
/
-/
.
!*
&
σ
#. #, / , .
/
/
/
*
/
,
/
-/
.
/
%
!*
%
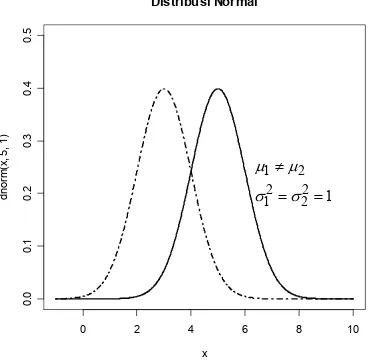
&
σ σ
≠
= =
/ , . $ /
/
/
/
*
/
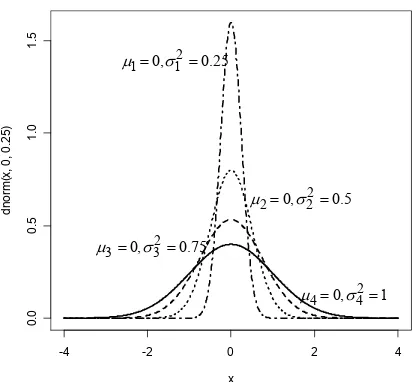
%
!*
/
/
,
%
&
σ
= =
σ
= =
#. #, / , .
/
/
/
%
*
σ
= =
σ
= =
/
.
/
/
$
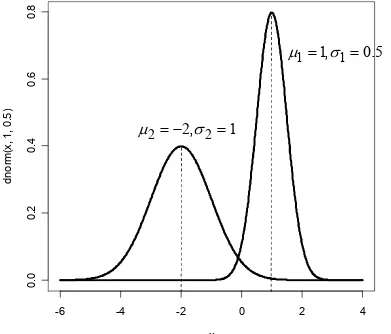
!*
/
%
&
σ
= =
σ
= − =
# #. #, / , .
/
/
/
,
*
Karakteristik Distribusi Normal
Data merupakan data kontinu (interval atau rasio)
Sebaran bersifat simetris dengan modus tunggal
(unimodal)
Mean=median=modus
Mean=median=modus
Batas nilai memungkinkan untuk seluruh bilangan
riil tak terbatas kekiri maupun kekanan
Perhitungan Probabilitas pada
Distribusi Normal
P(x1 < X < x2) =
=
∫
σ
[ − σ]
−
∫
=
Integral di atas tidak dapat diselesaikan secara analitis. Untuk memudahkan perhitungan tersedia tabel normal yang
berisikan luas dibawah area kurva normal baku
z=
[ ]
σ
π
∫
σ
Sifat Distribusi Normal
Grafik simetri terhadap sumbu tegak x (=μ)
Grafik selalu berada diatas sumbu X (f(X)>0)
Mempunyai satu nilai Modus
Grafik mendekati sumbu X (tidak akan memotong sumbu Grafik mendekati sumbu X (tidak akan memotong sumbu X)
Luas dibawah kurva f(X) dan diatas sumbu X sama
Kurva Normal
Kurva normal yang dibentuk oleh normal, memiliki bentuk lonceng simetris dan lebih lanjut memiliki properti sebagai berikut:
1.memiliki modus, median, dan mean pada satu titik
2.kurva berbentuk simetri terhadap sumbu vertikal yang 2.kurva berbentuk simetri terhadap sumbu vertikal yang
melewati
3.kurva memiliki titik belok pada x = ±σ
4.kurva normal mencapai sumbu horizontal secara
0
0 1
/ / / % / , /
( / 2% /
/ / % / , /
( / 22
. $ / , . / / / / / % / 3
( / 2%
- 2, /$ / /,% / /,% . $ / , . / / / / / % / 3
( / 22
% %, . $.$
Bentuk umum Kurva Distribusi
Normal
Disebut juga dengan Distribusi Gauss.
( )
=
π
σ
σ
σ
f(X)
σ
!" !
=
=
=
=
π
σ
π
σ
σ
X
*
(! * & !*& * σ *
πσ
−
−
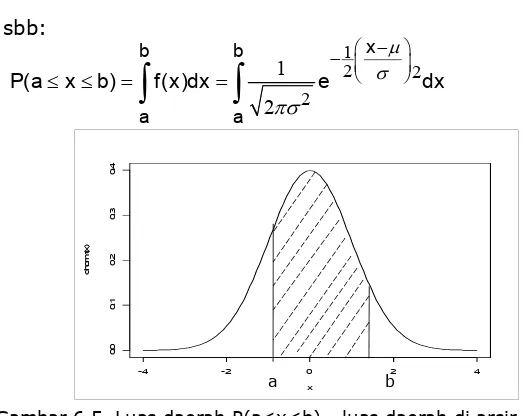
≤ ≤ =
∫
=∫
Luas daerah kurva normal antara x = a dan x = b dinyatakan sbb:
/
.
#. #, / , .
/
/
/
/
,
/
-*
!*
&
Fungsi padat perubah acak normal X, dengan rata0rata dan variansi dinyatakan sebagai:
* ! &! &
!*+ & σ + *
πσ
σ
− −
= −∞ < < ∞
σ
π = =
+ σ
= = !*+ &
Begitu dan diketahui, maka kurva normal dapat ditentukan. Misal:
maka ordinat dengan mudah dapat dihitung.
Untuk mengatasi kesulitan menghitung integral.
Gunakan tabel distribusi normal standart (Z) yaitu distribusi normal dengan
Caranya menggunakan transformasi dengan rumus
Setiap pengamatan perubah acak X dapat ditransformasikan ke perubah acak Z dengan rata0rata 0 dan variansi 1.
Jika X mendapat nilai padananya diberikan oleh . Jadi jika X bernilai dan maka perubah acak Z akan
σ
= =
*
4 = σ−
* 4 = σ−
* = * * = *
X bernilai dan maka perubah acak Z akan
Bernilai dan kemudian dinyatakan sebagai:
* = * * = *
*
4 = σ− 4 = * σ−
( ) * * 4 4 * 4 4
(!* * * & * *
!4 & * (!4 4 4 &
σ πσ πσ − − − ≤ ≤ = =
= = < <
∫
∫
/
,
/
-/
.
/
%
!*
/
"
%
&
#. #, / , .
/
/
/
*
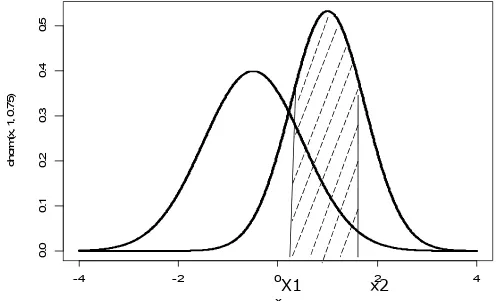
Gambar 6.6 P(x1<x<x2) untuk kurva normal yang berbeda
Distribusi perubah acak normal dengan rata0rata nol dan variansi 1 disebut distribusi normal baku
/ . / / $ !* # / % & / , / -/ . !* / & → #. #- #, # / , / / / , #. #, / , . / / / 4
Ganbar 6.7 Distribusi normal asli dan yang telah ditransformasikan
x1 x2 z1 z2
Probabilitas P(a<X<b)
P(a<X<b) ditentukan oleh luas daerah dibawah kurva f(X)
f(X) Menghitungnya luas daerah di bawah kurva f(X) dengan interval a dan b dilakukan dengan menggunakan
σ
#
=
X
a b
dilakukan dengan menggunakan rumus integral.
Probabilitas P(a<X<b)
(lanjutan)
B B+σ B+2σ B+3σ B03σ B02σ B0σ
0 1 2 3
03 02 01
Dengan transformasi tersebut maka diperoleh Distribusi Normal Z yang mempunyai rata0rata B = 0 dan simpangan baku σ = 1.
Probabilitas P(a<X<b)
(lanjutan)
f(X)
X 02 01 0 1 2 3
03
Probabilitas P(a<X<b)
(lanjutan)
Probabilitas P(z1<Z<z2) dihitung dengan memakai tabel Distribusi Normal Standar.
Contoh :
Tentukan probabilitas dari
(
<
#
≤
)
Tentukan probabilitas dari
Jawab :
Dari tabel diperoleh 0,4943
Maka = 0,4943
(
<
#
≤
)
(
<
#
≤
)
0 2,53
!
= σ =
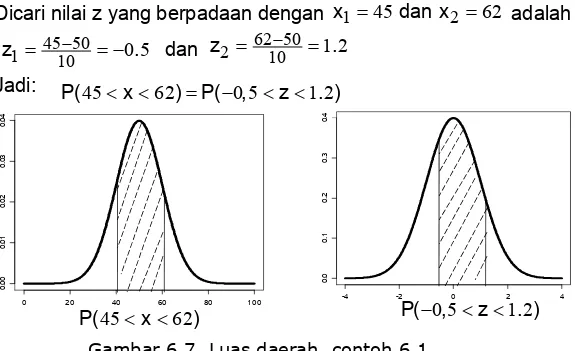
Diketahui suatu distribusi normal dengan
dan Carilah probabilitas bahawa X mendapat nilai
antara 45 dan 62
" #
4
5 6
$
* = * =
4 = − = − 4 = $ − =
$
(! < <* & = (!− < <4 &
/ . / / . #. #, / , . / / / / , / -/ . / ,/ ./ / $/ // / / / / / / / , / / -/ / . $
Gunakan tabel distribusi normal standart, diperoleh:
$
$
(! * & (! 4 &
(!4 & (!4 &
< < = − < <
= < − < −
= −
=
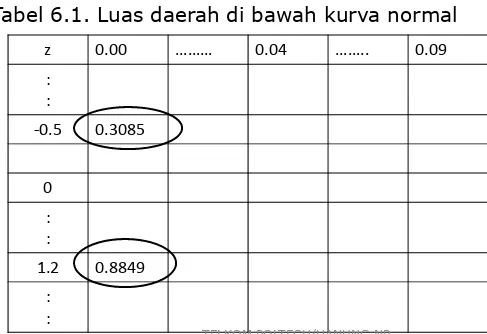
Tabel 6.1. Luas daerah di bawah kurva normal
z 0.00 ……… 0.04 …….. 0.09
: :
-0.5 0.3085
0
: :
PELUANG EKSAK
No B.Bawah B. Atas Luas
(Peluang)
1 Mean -1,645 Deviasi
Baku
Mean + 1,645 Deviasi Baku
90%
2 Mean -1,96 Deviasi
Baku
Mean +1,96 Deviasi Baku
95%
3 Mean -2,58 Deviasi
Baku
Mean +2,58 Deviasi Baku
LATIHAN
Hitung probabilitas dari nilai Z berikut :
P(Z<-1,75)
P(-2,75<Z<-1,52)
P(Z>-1,52)
P(Z>-1,52)
P(Z<0,97)
Bila X adalah variabel acak berdistribusi
Distribusi Kumulatif
Perhitungan probabilitas variabel random Z yang
berdistribusi normal standar akan lebih mudah dihitung dengan memakai fungsi distribusi kumulatif.
Distribusi kumulatif dari Z adalah F(z) dimana Distribusi kumulatif dari Z adalah F(z) dimana
F(z) = P(Z<z) sehingga :
(
) (
) (
)
( ) ( )
%
&
%
&
%
#
%
#
%
#
%
−
=
<
−
<
=
Hitung probabilitas dari P(-1,43<Z<2,53)
a. Dengan distribusi normal standar
b. Dengan distribusi kumulatif
Jawab:
a. P(-1,43<Z<2,53)=P(0<Z<1,43)+P(0<Z<2,53) =0,4236+0,4943=0,9179 b. P(-1,43<Z<2,53)=F(2,53)-F(-1,43)
Dari tabel distribusi normal standar kumulatif nilai z2=2,53 ada diantara 2,50 dan 2,55 juga diantara 2,326 dan 2,576. Kita pilih yang I.
Sedangkan nilai z1=-1,43 ada diantara -1,405 dan -1,476 juga diantara -1,40 dan -1,45. Kita pilih yang II.
Jika za=2,50 dan zb=2,55 kemudian Lz2=luas daerah (besar nilai) z2, Lza dan Lzb masing-masing untuk za dan zb maka besar z2 dapat dihitung dengan rumus :
'% '%
'% '%
% %
% %
Contoh Distribusi Normal
1. Tinggi badan mahasiswa ITB berdistribusi normal
dengan = 165 cm dan
σ
= 10 cm.
7
Berapa probabilitas seorang mahasiswa yang dipilih
7
Berapa probabilitas seorang mahasiswa yang dipilih
secara acak memiliki tinggi lebih dari 180 cm?
7
Tentukan ambang di mana persentase mahasiswa yang
Contoh Distribusi Normal
2. Sebuah pabrik lampu menghasilkan lampu dengan
usia nyala yang berdistribusi normal dengan =
2500 jam dan
σ
= 100 jam. Suatu batch dinyatakan
sebagai baik kalau dari 5 lampu yang diuji,
sebagai baik kalau dari 5 lampu yang diuji,
maksimum 1lampu yang usianya kurang dari 2350
jam. Berapa probabilitas suatu batch dinyatakan
baik? Kalau terjadi kerusakan pada proses produksi
sehingga -nya menjadi 2400 jam, berapa
Pendekatan Distribusi Normal
Terhadap Distribusi Binomial
Pada saat n sangat besar dan p tidak bernilai ekstrim mendekati 0
atau 1, perhitungan terhadap distribusi binomial dapat dilakukan dengan menggunakan pendekatan perhitungan distribusi normal. Teorema:
Teorema:
Jika X adalah sebuah variabel random binomial dengan mean = np
dan variansi σ2 = npq, maka bentuk limit pada saat n ∞ dari
distribusi binomial tersebut adalah:
dengan z berdistribusi normal baku n(z; 0,1)
Pendekatan Dist. Normal atas Dist. Binomial
(Contoh)
LATIHAN
1. Jika diketahui variabel random X mempunyai distribusi
normal dengan rata-rata 18 dan standar deviasi 2,5 hitung nilai k sehingga P(X<k)=0,2578!
2. Sebanyak 1000 rim kertas koran dengan berat 60 gram
diketahui bahwa rata-rata tiap rimnya berisi 450 lembar dengan standar deviasi 10 lembar. Jika distribusi jumlah dengan standar deviasi 10 lembar. Jika distribusi jumlah kertas per rim tersebut berdistribusi normal, berapa
LATIHAN (lanjutan)
3. Nilai ujian statistika sebagian besar mahasiswa mempunyai distribusi
normal dengan rata-rata 34 dan standar deviasi 4. Jika X menyatakan nilai-nilai mahasiswa tersebut, berapakah batas nilai Xo agar 10% dari kelompok nilai terendah berada dibawah Xo?
4. Dari 200 mahasiswa yang mengikuti ujian Statistika diperoleh nilai
rata-ratanya adalah 60 dan standar deviasinya adalah 10. Bila distribusinya menyebar secara normal, berapa :
distribusinya menyebar secara normal, berapa : a. persen yang mendapat nilai A jika nilai A>=80 b. persen yang mendapat nilai C jika nilai C terletak
pada interval 56<=C<=68
LATIHAN (lanjutan)
5. Suatu percobaan mengenai ukuran ruang memori dengan menggunakan
metode Quickshort menyatakan bahwa ukuran penggunaan ruang memori berdistribusi normal dengan rata-rata 510,8 byte dan simpangan baku 40,67 byte.
a. Berapa persen dalam percobaan tersebut
ditemukan ruang memori yang melebihi 600 byte? b. Jika ditemukan 10 buah percobaan mempunyai b. Jika ditemukan 10 buah percobaan mempunyai ruang memori berkisar antara 500 sampai 550
byte, berapakah jumlah percobaan yang telah dilakukan oleh peneliti?
c. Jika dalam percobaan tersebut ditemukan bahwa 10% hasil terendah, berapakah ukuran memori tertinggi dari kelompok hasil percobaan dengan ukuran memori