OPERASI GABUNGAN, JOIN, KOMPOSISI DAN HASIL KALI KARTESIAN PADA GRAF FUZZY SERTA KOMPLEMENNYA. Tina Anggitta Novia 1 dan Lucia Ratnasari 2

(1)

159

Tina Anggitta Novia dan Lucia Ratnasari

1,2

Program Studi Matematika FMIPA UNDIP Jl. Prof. Soedarto, SH, Semarang, 50275

Abstract. A fuzzy graphs G: V

(

,σ,µ

)

is a nonempty set Vtogether with a pair function

[ ]

0,1 :V →

σ and µ:VxV →

[ ]

0,1 satisfied µ

( )

uv ≤σ

( )

u ∧σ

( )

v ∀u v V, ∈ . This paper described about some operations on fuzzy graphs such as union, join, compositions and cartesian product. Complement of union two fuzzy graphs is join of their complement, join complement of two fuzzy graphs is union their complement. Complement of composition two strong fuzzy graphs is composition of their complement, but complement of cartesian product two stong fuzzy graphs is need not cartesian product of their complement.

Keywords : cartesian product, complement, compositions, fuzzy graphs, join

1. PENDAHULUAN

Teori graf merupakan salah satu

bidang bahasan matematika yang

mempelajari himpunan titik yang dihubungkan oleh himpunan garis [1], [5]. Himpunan kabur adalah suatu himpunan dimana nilai keanggotaan dari elemennya adalah bilangan riil dalam interval tertutup [0,1] [4]. Teori graf fuzzy pertama kali diperkenalkan oleh Azriel Rosenfeld pada tahun 1975 yang merupakan suatu perluasan dari teori graf dan himpunan kabur (fuzzy set). Seiring dengan perkembangan jaman maka konsep graf fuzzypun juga semakin berkembang.

Komplemen graf fuzzy pertama kali diperkenalkan oleh Mordeson yang kemudian disempurnakan oleh M.S. Sunitha dan Vijayakumar. Pada tulisan ini akan dibahas mengenai operasi gabungan, join, komposisi dan hasil kali Cartesian pada graf fuzzy kemudian akan diselidiki komplemennya.

2. GRAF FUZZY

Definisi 2.1. [2] Misalkan _{V himpunan} titik berhingga, suatu graf fuzzy yang dinotasikan dengan G: V

(

,σ,µ

)

_atau

disingkatG:

( )

σ,µ adalah sepasang fungsi dengan i. σ :V →

[ ]

0,1 ii. µ:VxV →

[ ]

0,1 yang memenuhi

( ) ( ) ( )

uv ≤σ u ∧σ v ∀u,v∈V µ .

Contoh 2.1 Misalkan diberikan graf fuzzy G dengan himpunan titik V =

{

a,b,c,d,e

}

dan himpunan garis

( ) ( ) ( ) ( ) ( )

{

ab be cd ce de

}

E= , , , , .

Derajat keanggotaan dari himpunan titiknya adalah

( )

a =0.6 ,σ

( )

b =0.3,σ

( )

c =0.6,

σ

( )

d =0.4,σ

( )

e =0.5

σ dan derajat

keanggotaan dari himpunan garisnya adalah

( )

ab =0.3 ,µ

( )

be =0.1 ,µ

( )

cd =0.2 µ

( )

ce =0.5 ,µ

( )

de =0.3 µ , maka graf fuzzy G tersebut :

(2)

Tina Angitta Novia dan Lucia Ratnasari (Operasi Gabungan, Join, Komposisi dan Hasil Kali Kartesian …)

160

(σ,µ)

: G

Gambar 1. Graf fuzzy

Definisi 2.2 [2] Suatu graf fuzzy G:

(

σ,µ

)

adalah graf fuzzy kuat jika

( ) ( ) ( ) ( )

₌_σ _∧_σ _∀ _∈_µ∗

µ uv u v, uv .

Contoh 2.2 Misalkan diberikan graf fuzzy dengan graf dasarnya

( )∗ ∗ ∗_:_σ_,_µ G ( )σ,µ : G

Gambar 2. Graf fuzzy G dan graf dasarnya

maka graf fuzzy tersebut merupakan graf

fuzzy kuat karena

( ) ( ) ( ) ( )

₌_σ _∧_σ _∀ _∈_µ∗

µ uv u v, uv .

Definisi 2.3 [3] Komplemen dari suatu

graf fuzzy G:

( )

σ,µ adalah suatu graf fuzzy yang dinotasikan G:

( )

σ,µ ,dimana

i. σ =σ dan

ii. µ

( ) ( ) ( ) ( )

uv =σ u ∧σ v −µ uv∀u,v∈V Contoh 2.3 Misalkan diberikan graf fuzzy pada Contoh 2.1 maka komplemen dari graf fuzzy tersebut adalah :

( )

σ,µ

:

G

Gambar 3. Komplemen dari garf fuzzy G

3. OPERASI GABUNGAN, JOIN, KOMPOSISI DAN HASIL KALI KARTESIAN PADA GRAF FUZZY Definisi 3.1 [3] Misalkan G₁:

(

σ₁,µ₁

)

dan

(

2 2

)

2: σ ,µ

G adalah dua graf fuzzy dengan

(

1 1

)

1 : V,E G∗ dan G₂∗ :

(

V₂,E₂

)

dan φ = ∩ 2 1 V V . Misalkan

(

1 2 1 2

)

2 1 G V V ,E E G G∗ = ∗∪ ∗ = ∪ ∪

merupakan gabungan dari G dan ₁∗ G , ₂∗ maka gabungan dari graf fuzzy G dan ₁ G ₂ adalah sebuah graf fuzzy

(

1 2 1 2

)

2 1∪ : σ ∪σ ,µ ∪µ =G G G dengan

(

)( )

( )

_{( )}

   ∈ ∈ = ∪ 2 2 1 1 2 1 V u jika u V u jika u u σ σ σ σ dan

(

)( )

( )

_{( )}

   ∈ ∈ = ∪ 2 2 1 1 2 1 E uv jika uv E uv jika uv uv µ µ µ µ

Contoh 3.1 Misalkan diberikan graf fuzzy

(

1 1

)

1: σ ,µ

G dan G₂:

(

σ₂,µ₂

)

:

Gambar 4. Graf fuzzy G₁ dan graf fuzzy G₂

Sehingga gabungan dari graf fuzzy

(

1 1

)

1: σ ,µ

(3)

161

2

1 G

G ∪

Gambar 5. Gabungan dari graf fuzzy G₁ dan graf fuzzy G₂

Definisi 3.2 [3] Misalkan G₁:

(

σ₁,µ₁

)

dan

(

2 2

)

2 : σ ,µ

(

1 1

)

1 : V,E G∗ , G₂∗ :

(

V₂,E₂

)

(

₁ ₂, ₁ ₂ '

)

2 1 G V V E E E G G∗ = ∗+ ∗ = ∪ ∪ ∪

dimana E' adalah himpunan semua garis yang menghubungkan semua titik dari V1 dan V2 .Maka join dari graf fuzzy G dan ₁

2

G adalah sebuah graf fuzzy

(

1 2 1 2

)

2 1 + : σ +σ ,µ +µ =G G G dengan

(

σ1+σ2

)( ) (

u = σ1∪σ2

)( )

u jika u∈V1∪V2 dan

(

)( ) (

_{( )}

)( )

_{( )}

   ∈ ∧ ∪ ∈ ∪ = + ' 2 1 2 1 2 1 2 1 E uv jika v u E E uv jika uv uv σ σ µ µ µ µ

(

1 1

)

1: σ ,µ

G dan G₂:

(

σ₂,µ₂

)

pada Contoh 3.1 sehingga join dari kedua graf fuzzy tersebut adalah :

Gambar 6. Join dari graf fuzzy G₁ dan graf fuzzy G₂

Teorema 3.1 [3] Misalkan G₁ :

(

σ₁,µ₁

)

dan G₂ :

(

σ₂,µ₂

)

merupakan 2 graf fuzzy, maka :

1) G₁+G₂ =G₁∪G₂

2) G₁∪G₂ =G₁+G₂ Bukti :

1) Akan dibuktikan bahwa

2 1 2 1 G G G G + = ∪ , akan dibuktikan

( )

u

(

1 2

)

( )

u 2 1 σ σ σ σ + = ∪ dan µ₁ +µ₂

( )

uv =µ₁∪µ₂

( )

uv : ( i ). σ1 +σ2

( ) (

u = σ1 +σ2

)( )

u , dengan

definisi dari komplemen

(

1 ∪ 2

)( )

u jikau∈V1 ∪V2 = σ σ

( )

   ∈ ∈ = 2 2 1 1 , , V u jika u V u jika u σ σ

( )

(

)

( )

u V u jika u V u jika u 2 1 2 2 1 1 , , σ σ σ σ ∪ =    ∈ ∈ = Sehingga σ1+σ2

( )

u =

(

σ1∪σ2

)

( )

u ( ii ).

(

)

( ) ( )( ) ( )( ) ( )( ) 1 2 1 2 1 2 1 2 uv u v uv µ µ σ σ σ σ µ µ + = + ∧ + − +

(

)( ) (

)( )

(

)

(

)( ) (

)( )

(

( )

)

1 2 1 2 1 2 1 2 1 2 1 2 1 2 , , ' u v uv jika uv E E u v u v jika uv E σ σ σ σ µ µ σ σ σ σ σ σ ∪ ∧ ∪ − ∪   ∈ ∪  =  ∪ ∧ ∪ − ∧   _∈ 

( )

(

( )

)

1 1 1 1 2 2 2 2 1 2 1 2 1 2 , , , ' , u v uv jika uv E u v uv jika uv E u v u v jika uv E dan u V v V σ σ µ σ σ µ σ σ σ σ  ∧ −  ∈   _∧ ₋  =  _∈   _∧ ₋ _∧   _∈ _∈ _∈ 

(4)

Tina Angitta Novia dan Lucia Ratnasari (Operasi Gabungan, Join, Komposisi dan Hasil Kali Kartesian …) 162

( )

uv E uv jika uv E uv jika uv 2 1 2 2 1 1 0 , ,

µ

∪ =      ∈ ∈ = Sehingga µ₁+µ₂

( )

uv =µ₁ ∪µ₂

( )

uv

Dari (i) dan (ii) terbukti G₁+G₂ =G₁∪G₂

2) Akan dibuktikan bahwa

2 1 2 1 G G G G ∪ = + , yaitu ditunjukkan

( )

u

(

1 2

)

( )

u 2 1 σ σ σ σ ∪ = + dan

( )

uv

(

1 2

)

( )

uv 2 1 µ µ µ µ ∪ = + , ( i ). σ₁∪σ₂

( ) (

u = σ₁∪σ₂

)( )

u dengan definisi komplemen

( )

(

)

( )

(

)

( )

u u V u jika u V u jika u V u jika u V u jika u 2 1 2 1 2 2 1 1 2 2 1 1 , , , , σ σ σ σ σ σ σ σ + = ∪ =    ∈ ∈ =    ∈ ∈ = Sehingga σ₁∪σ₂

( )

u =

(

σ₁ +σ₂

)

( )

u (ii). 1

₍

2

( )

_{)( ) (}

_{)( )}

1 2 1 2 1 2 uv u v uv µ µ σ σ σ σ µ µ ∪ = ∪ ∧ ∪ − ∪

( )

1 1 1 1 2 2 2 2 1 1 1 2 , , 0, , ' u v uv jika uv E u v uv jika uv E u v jika u V v V dan uv E σ σ µ σ σ µ σ σ  ∧ −  _∈   _∧ ₋  =  _∈   _∧ ₋   ∈ ∈ ∈ 

( )

(

)

( )

(

)

( )

1 1 2 2 1 1 1 2 1 2 1 2 1 1 1 2 , , , , , , ' uv jika uv E uv jika uv E u v jika u V v V uv jika uv E E u v jika uv E uv µ µ σ σ µ µ σ σ µ µ   ∈    =  ∈   _∧   ∈ ∈   _∪ _{∈ ∪}  =  ∧ ∈  = + Sehingga µ₁∪µ₂

( )

uv =

(

µ₁+µ₂

)

( )

uv

Dari (i) dan (ii) terbukti

2 1 2

1 G G G

G ∪ = + .

Dari 1 dan 2 terbukti bahwa komplemen dari join 2 graf fuzzy merupakan gabungan dari komplemennya dan komplemen dari gabungan 2 graf fuzzy merupakan join dari gabungannya .

(

1 1

)

1: σ ,µ

G dan G₂:

(

σ₂,µ₂

)

pada Contoh 3.1

1) Akan ditunjukkan bahwa

2 1 2 1 G G G G + = ∪ , ( i ). G₁+G₂

Gambar join dari dua graf fuzzy diatas dapat dilihat pada Gambar 6 di Contoh 3.2, sehingga 2 1 G G + = 2 1 G G +

(5)

163 Gambar 7. Komplemen dari join graf fuzzy G₁

dan graf fuzzy G₂ ( ii ). G dan 1

G

₂

1

G

2

G

Gambar 8. Komplemen dari graf fuzzy G₁ dan graf fuzzy G₂ 2 1 G G ∪ = 2 1 G G ∪

Gambar 9. gabungan dari komplemen graf fuzzy

1

G dan graf fuzzy G₂

Sehingga dari (i) dan (ii) diperoleh

2 1 2

1 G G G

G + = ∪

2) Akan ditunjukkan bahwa

2 1 2 1 G G G G ∪ = + , ( i ). G₁ ∪G₂

Gambar gabungan dari dua graf fuzzy diatas dapat dilihat pada Gambar 5 di Contoh 3.1, sehingga

2 1 G G ∪ ₌ 2 1 G G∪

Gambar 11. komplemen dari gabungan graf fuzzy

1

G dan graf fuzzy G₂

( ii ). Gambar komplemen G ₁ dan komplemen G₂ dari dua graf fuzzy diatas dapat dilihat pada Gambar 11, sehingga 2 1 G G + = 2 1 G G+

Gambar 12. Join dari komplemen graf fuzzy G₁dan graf fuzzy G₂

Sehingga dari (i) dan (ii) diperoleh

2 1 2

1 G G G

G ∪ = + .

Sehingga dari 1 dan 2 terbukti bahwa komplemen dari join 2 graf fuzzy merupakan gabungan dari komplemennya dan komplemen dari gabungan 2 graf fuzzy merupakan join dari gabungannya .

Definisi 3.3. [3] Misalkan G₁:

(

σ₁,µ₁

)

dan

(

2 2

)

2 : σ ,µ

(

1 1

)

1 : V,E G∗ , G₂∗ :

(

V₂,E₂

)

dan φ = ∩ 2 1 V V dan misalkan

(

V V E

)

G G G∗ = ₁∗o ₂∗ = ₁× ₂, adalah komposisi dari dua graf, dimana

(

)( )

{

}

(

)(

)

{

}

(

)(

)

{

1 2 1 2 1 1 1 2 2

}

1 1 1 2 1 1 2 2 2 1 2 2 , : , , , : , , , : , , v u E v u v v u u E v u V w w v w u E v u V u v u u u E ≠ ∈ ∪ ∀ ∈ ∀ ∪ ∈ ∀ ∈ ∀ =

(6)

164

Maka komposisi dari graf fuzzy

(

1 2 1 2

)

2

1o = σ oσ ,µ oµ

=G G

G adalah

graf fuzzy yang di definisikan oleh :

(

σ1oσ2

)(

u1,u2

)

=σ1

( )

u1 ∧σ2

( ) (

u2 ,∀u1,u2

)

∈V1×V2 dan ( ) (( )( )) ( ) ( ) ( ) (( )( )) ( ) ( ) ( ) (( )( )) ( ) ( ) ( ) (, , )( , ) '' , , ; , , , , ; , , , , 2 1 2 1 1 1 1 2 2 2 2 2 1 2 1 2 1 1 1 1 2 1 1 1 2 1 1 2 1 2 2 2 1 2 2 2 1 2 2 2 1 E E v v u u v u v u v v u u E v u V w v u w w v w u E v u V u v u u v u u u − ∈ ∀ ∧ ∧ = ∈ ∀ ∈ ∀ ∧ = ∈ ∀ ∈ ∀ ∧ = µ σ σ µ µ µ σ µ µ µ σ µ µ o o o dimana ( )( ) { } ( )( ) { 1 1 2 1 1 1} 2 2 2 1 2 2 , : , , , : , , '' E v u V w w v w u E v u V u v u u u E ∈ ∀ ∈ ∀ ∪ ∈ ∀ ∈ ∀ =

(

1 1

)

1: σ ,µ

G dan G₂:

(

σ₂,µ₂

)

pada Contoh 3.1 sehingga komposisi dari kedua graf fuzzy tersebut adalah :

2 1 G

G o

Gambar 13. Komposisi dari graf fuzzy G₁ dan graf fuzzy G₂

Teorma 3.2. [3] Misalkan G₁

(

σ₁,µ₁

)

dan

(

2 2

)

2 σ ,µ

G adalah dua graf fuzzy kuat maka G₁oG₂ =G₁oG₂ .

Bukti :

Untuk membuktikan bahwa

2 1 2 1 G G G G o = o _, Misalkan G =G₁oG₂ =G:

( )

σ,µ dimana 2 1 2 1 σ ,µ µ µ σ σ = o = o

( )

, , : G1 G2 G σ µ = o dimana

( )

V E G dan , 2 1 = =_µ _µ ∗ µ o

(

,

)

( )

, ; : ₁ ₁ ₁ ₁ ₁ 1 G V E G σ µ = ∗ =

(

,

)

(

,

)

; : ₂ ₂ ₂ ₂ ₂ 2 G V E G σ µ = ∗ = dan

(

1 2 1 2

)

2 1o G : σ oσ ,µ oµ G

Untuk pembuktian di bawah ini garis yang menghubungkan dua titik di notasikan dengan e .

Untuk membuktikan µ₁oµ₂ =µ₁oµ₂ dibuktikan dalam beberapa kasus

Kasus 1.

(

u,u2

)(

u,v2

)

,u2v2 E2

e= ∈

karena e∈Edan G graf fuzzy kuat maka

( )

e =0 µ . Juga

(

µ1oµ2

)

( )

e =0 karena u₂v₂ ∉E₂ . sehingga

(

µ₁oµ₂

)( )

e =

(

µ₁oµ₂

)

( )

e Kasus 2.

(

u,u2

)(

u,v2

)

,u2v2 E2 e= ∉ karena e∉E, sehingga µ

( )

e =0,

( ) (

) (

) ( )

(

) (

)

(

) (

)

( )

(

)

(

( )

)

( )

, , , 0 , , , , 2 2 2 2 1 2 2 1 2 2 1 2 2 2 2 2 2 v u u v u u u v u u u v u u u e v u u u e σ σ σ σ σ σ σ σ σ σ σ µ σ σ µ ∧ ∧ = ∧ ∧ ∧ = ∧ = − ∧ = − ∧ =

dan karena u₂v₂∈E₂, maka

(

)

( )

(

)

( )

e v u u v u u e µ σ σ σ µ σ µ µ = ∧ ∧ = ∧ = 2 2 2 2 1 2 2 2 1 2 1o sehingga

(

µ1oµ2

)( )

e =

(

µ1oµ2

)

( )

e Kasus 3.

(

u1,w

)(

v1,w

)

,u1v1 E1 e= ∈ karena e∈E, maka µ

( )

e =0 .

Kemudian, karena u₁v₁∉E₁ maka

(

µ1oµ2

)

( )

e =0,

(7)

165 Kasus 4.

(

u1,w

)( )

v1,w,u1v1 E1

e= ∉

karena e∉E,maka µ

( )

e =0 dan

( ) (

) (

) ( )

(

) (

)

(

) (

)

( )

, , , 0 , , , , 2 1 1 1 1 1 1 1 1 1 1 w v u w v w u w v w u e w v w u e σ σ σ σ σ σ σ µ σ σ µ ∧ ∧ = ∧ = − ∧ = − ∧ =

dan karena u₁v₁∈E₁di dapat sehingga

(

µ1oµ2

)( )

e =

(

µ1oµ2

)

( )

e

Kasus 5.

(

u1,u2

)(

v1,v2

)

,u1v1 E1 danu2 v2

e= ∈ ≠

karena e∈E, maka µ

( )

e =0 ,

Kemudian, karena u1v1∉E1 maka

(

µ1oµ2

)

( )

e =0, sehingga

(

µ₁oµ₂

)( )

e =

(

µ₁oµ₂

)

( )

e Kasus 6.

(

u1,u2

)(

v1,v2

)

,u1v1 E1 danu2 v2 e= ∉ ≠ karena e∉E, maka µ

( )

e =0

( ) (

) (

) ( )

(

) (

)

(

) (

)

( )

1 1

( )

1 2

( )

2 2

( )

2 1 2 1 2 1 2 1 2 1 2 1 2 1 , , 0 , , , , v u v u v v u u v v u u e v v u u e σ σ σ σ σ σ σ σ µ σ σ µ ∧ ∧ ∧ = ∧ = − ∧ = − ∧ =

dan karena u₁v₁∈E₁, di dapat

( )

e v u v u v u v u µ σ σ σ σ σ σ µ µ µ = ∧ ∧ ∧ = ∧ ∧ = , 2 2 2 2 1 1 1 1 2 2 2 2 1 1 2 1o sehingga

(

µ₁oµ₂

)( )

e =

(

µ₁oµ₂

)

( )

e

Dari kasus 1 sampai kasus 6, ini membuktikan bahwa G₁oG₂ =G₁oG₂ .

Contoh 3.6 Misalkan diberikan dua graf

1

G dan G yang merupakan graf fuzzy ₂ kuat , yaitu :

1

G G2

Gambar 14. Graf fuzzy kuat G₁dan Graf fuzzy kuat G₂

maka,

2

1 G

G o

Gambar 15. Komposisi dari graf fuzzy kuat G₁ dan graf fuzzy kuat G₂

2 1 G

G o

Gambar 16. komplemen dari komposisi dua graf fuzzy kuat

1

G G2

Gambar 17. Komplemen dari graf fuzzy kuat G₁ graf fuzzy kuat G₂

( )

e v u w v u w e µ σ σ σ µ σ µ µ = ∧ ∧ = ∧ = , 1 1 1 1 2 1 1 1 2 2 1o

(8)

166

Gambar 18. Komposisi dari komplemen 2 graf fuzzy kuat

Sehingga didapat bahwa jika G dan ₁ G ₂ merupakan graf fuzzy kuat maka

2 1 2

1 G G G

G o = o ,

Definisi 3.4 [3] Misalkan G₁:

(

σ₁,µ₁

)

dan

(

2 2

)

2 : σ ,µ

(

1 1

)

1 : V,E G∗ , G₂∗ :

(

V₂,E₂

)

(

, ''

)

2 1 G V E G G∗ = ∗× ∗ = adalah cartesian product dari dua graf dimana

2 1 V V V = × dan

(

)(

)

{

}

(

)(

)

{

1 1 2 1 1 1

}

2 2 2 1 2 2 , : , , , : , , '' E v u V w w v w u E v u V u v u u u E ∈ ∀ ∈ ∀ ∪ ∈ ∀ ∈ ∀ = .

maka cartesian product dari

(

1 2 1 2

)

2

1× : σ ×σ ,µ ×µ

=G G

G adalah

graf fuzzy yang di definisikan oleh :

(

σ₁×σ₂

)(

u₁,u₂

)

=σ₁

( )

u₁ ∧σ₂

( ) (

u₂ ∀u₁,u₂

)

∈V dan

(

)(

)

(

)

( )

(

)

(

)(

)

(

)

( )

1

( )

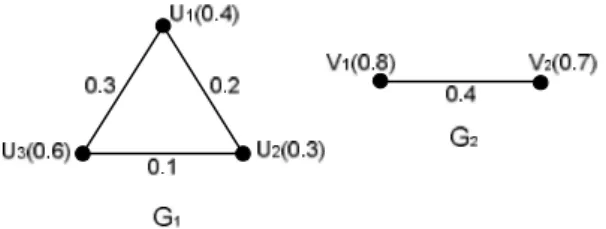
1 1 2 1 1 1 2 1 1 2 1 2 2 2 1 2 2 2 1 2 2 2 1 , , , , , , , , E v u V w v u w w v w u E v u V u v u u v u u u ∈ ∀ ∈ ∀ ∧ = × ∈ ∀ ∈ ∀ ∧ = × µ σ µ µ µ σ µ µ

Cotoh 3.7 Misalkan diberikan graf fuzzy

(

1 1

)

1: σ ,µ

G dan G₂:

(

σ₂,µ₂

)

pada Contoh 3.1, sehingga Cartesian product dari kedua graf fuzzy tersebut adalah :

2 1 G

G×

Gambar 19. Cartesian product dari graf fuzzy G₁ dan graf fuzzy G₂

Misalkan G₁

(

σ₁,µ₁

)

dan G₂

(

σ₂,µ₂

)

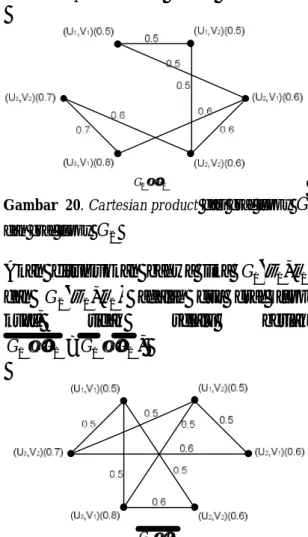
adalah dua graf fuzzy kuat, maka tidak selalu berlaku G₁×G₂ =G₁×G₂ .

Contoh 3.8 Misalkan di berikan graf fuzzy kuat G₁

(

σ₁,µ₁

)

dan G₂

(

σ₂,µ₂

)

pada Contoh 3.6 pada Gambar 14 , maka cartesian product-nya adalah

2

1 G

G×

Gambar 20. Cartesian product dari graf fuzzy G₁ dan graf fuzzy G₂

Akan ditunjukkan bahwa jika G₁

(

σ₁,µ₁

)

dan G₂

(

σ₂,µ₂

)

adalah dua graf fuzzy

kuat, tidak selalu berlaku

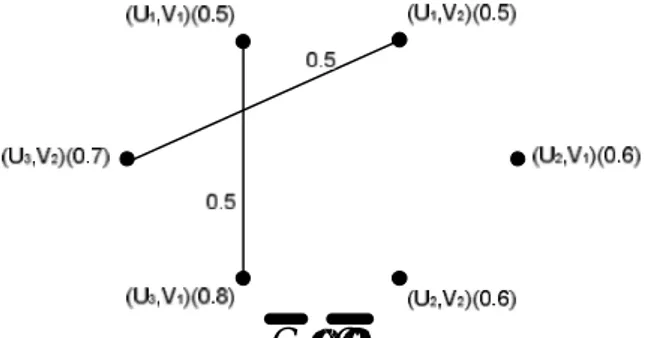
2 1 2 1 G G G G × = × , 2 1 G G×

Gambar 21. Komplemen dari Cartesian product dua graf fuzzy kuat

(U1,V1)(0.5) (U3,V1)(0.8) (U2,V2)(0.6) (U1,V2)(0.5) (U2,V1)(0.6) (U3,V2)(0.7) 0.5 0.5 0.5 0.5 2 1 G G o

(9)

167

berdasarkan komplemen graf fuzzy kuat

1

G dan graf fuzzy kuat G pada Gambar ₂ 21, maka diperoleh :

2

1 G

G ×

Gambar 22. Cartesian product dari komplemen dua graf fuzzy kuat G₁ dan graf fuzzy kuat G₂

Sehingga didapat bahwa jika G₁

(

σ₁,µ₁

)

dan G₂

(

σ₂,µ₂

)

adalah dua graf fuzzy kuat, maka tidak selalu berlaku

2 1 2 1 G G G G × = × . 4. PENUTUP

Berdasarkan pembahasan yang telah diuraikan diperoleh:

1. Komplemen dari gabungan dua graf fuzzy adalah join dari komplemennya.

2. Komplemen dari join dua graf fuzzy adalah gabungan dari komplemennya. Komplemen dari komposisi dua graf fuzzy kuat adalah komposisi dari komplemennya.

3. Jika terdapat dua graf fuzzy kuat, tidak selalu berlaku komplemen dari hasil kali Cartesian dua graf fuzzy adalah

hasil kali Cartesian dari

komplemennya.

5. DAFTAR PUSTAKA

[1] Chartrand, G dan L. Lesniak., (1996), Graphs & Digraphs. New York : Drew University

[2] Mordeson, J.N, & Nair , P., (2000), Fuzzy graphs and Fuzzy hypergraphs. Physica-Verlag : New York.

[3] Sunita, M.S dan A. Vijaya Kumar, (2002), Complement of A Fuzzy Graph. Indian J. Pure Applied Mathematical, 33:9 hal 1451 – 1464. [4] Susilo, F., (2006), . Himpunan dan

Logika Kabur serta Aplikasinya. Yogyakarta : Graha Ilmu.

[5] Wilson, J. et. al., (1990), Graphs An Introductory Approach. New York : University Course Graphs, Network, and Design.