1. Menentukan besaran pokok, besaran turunan dan satuannya atau penggunaan alat ukur dalam kehidupan sehari-hari.

INDIKATOR UN 2013

1. Dalam Fisika ada 7 buah besaran pokok

BESARAN POKOK SATUAN mks/SI SATUAN cgs

Panjang (l) Meter (m) cm

Massa (m) Kilogram (kg) gram (g)

Waktu (t) sekon (s) sekon(s)

Suhu (t,T) kelvin (K) -

Kuat arus listrik (I) ampere (A) -

Intensitas Cahaya Candela (Cd) -

Jumlah zat Mole (mol) -

Selain 7 besaran pokok, besaran yang lain merupakan besaran turunan yang satuannya tergantung dari satuan-satuan besaran pokok yang menyusun rumus besaran tersebut.

Contoh :

BESARAN RUMUS SATUAN SI

Volume (V) V = p  l  t m.m.m = m3 Kecepatan(v) v = s/t m/s Massa Jenis  = m/V kg/m3 Berat (w) w = m  g kg.m/s2 = N Tekanan (P) P = F/A N/m2 = Pa Alat ukur

- ALAT UKUR PANJANG a. Mistar

Mistar memiliki skala terkecil mm sehingga memiliki ketelitian ±1 mm.

Dari contoh di atas maka panjang benda yang diukur adalah 20 cm – 16,6 cm = 3,4 cm

b. Jangka sorong

Jangka sorong memiliki skala utama dan skala tambahan ( nonius). Ketelitian alat ukur ini adalah ± 0,1 mm atau 0,01 cm ( skala terkecil pada skala nonius )

1. Menentukan besaran pokok, besaran turunan dan satuannya atau penggunaan alat ukur dalam kehidupan sehari-hari .

15 16 17 18 19 20 20 benda Skala utama Skala nonius 1 2 3 0 5 7 10

Cara membaca skala dengan menggunakan jangka sorong dari contoh di atas adalah

- Lihat skala nonius skala 0 terletak sesudah skala 1,0 pada skala utama.

- Lihat skala utama dan skala nonius yang berhimpit yaitu skala 7

- Jadi yang diukur 1,0 cm + 0,07 cm = 1,07 cm .

b. Mikrometer sekrup

Sama seperti jangka sorong, micrometer sekrup memiliki skala utama dan skala nonius.

Ketelitian ukur mikrometer sekrup adalah 0,01 mm.

Cara menggunakan skala mikrometer sekrup pada contoh di atas adalah

- Lihat skala utama yang terlihat dari luar : 3,5 mm

- Lihat skala nonius yang berhimpit dengan skala utama : 8 = 0,08 mm

- Jadi yang diukur adalah : 3,5 mm + 0,08 mm = 3,58 mm

- ALAT UKUR MASSA

Untuk mengukur massa benda digunakan neraca atau timbangan. Jenuis neraca yang kita kenal :

1. Neraca pasar

2. Neraca 1 lengan

3. Neraca 2 lengan

4. Neraca 3 lengan

5. Neraca pegas

6. Neraca elektronik /digital

Contoh Soal

1. Berapa massa benda yang diukur saat timbangan menunjukkan posisi seperti tampak pada gambar di bawah ini ?

Berdasarkan contoh di atas , massa yang diukur adalah : 300 g + 60 g + 5,5 g = 365,5 g

0 1 2 3 5 10 15 0 Skala utama Skala nonius 50 60 70 80 90 100g 4 5 6 7 8 9 10g 200 300 400 500 g

ALAT UKUR VOLUME

Untuk mengukur volume benda yang bentuknya tidak teratur (zat cair , batu dsb) digunakan gelas ukur (1) atau gelas ukur dan gelas berpancuran. (2)

ALAT UKUR SUHU

Untuk mengukur suhu digunakan termometer. Termometer yang cukup dikenal adalah termometer Celcius , Reamur, Fahrenheit dan Kelvin. Zat cair pengisi termometer adalah raksa atau alkohol . Contoh Soal

01. Perhatikan tabel berikut !

No Besaran Satuan(dalam SI) Alat ukur

(1) Suhu celsius Termometer

(2) Waktu sekon Stopwatch

(3) Massa kilogram Neraca

(4) Panjang meter Speedometer

Berdasarkan tabel di atas, besaran dengan satuan dalam Sistem Internasional dan alat ukur yang sesuai ditunjukkan oleh nomor....

A. (1) dan (2) C. (2) dan (4)

B. (2) dan (3) D. (3) dan (4)

Jawab : B INDIKATOR UN 2013

ADA TIGA WUJUD ZAT - Zat padat

- Zat cair - Gas

Susunan partikel dan masing-masing zat a. ZAT PADAT

Partikel-partikel zat padat sangat berdekatan, susunannya teratur dan ikatan antar partikel

sangat kuat. Oleh sebab itu zat padat memiliki sifat bentuk dan volumenya tetap.

2. Menentukan sifat-sifat zat berdasarkan wujudnya atau penerapan dalam kehidupan sehari-hari.

1 2

Berdasarkan contoh, hasil pengukuran volume batu dengan gelas ukur (1) adalah :

80 ml – 50 ml = 30 ml.

Pada contoh (2) hasil pengukuran volume benda adalah : 200 ml

b.ZAT CAIR

Partikel-partikel zat cair agak berjauhan , ikatan antar partikel agak lemah , dapat berpindah tempat

tetapi tidak dapat meninggalkan kelompoknya. Oleh sebab itu zat cair memiliki sifat bentuk dapat

berubah sesuai bentuk tempatnya tetapi volumenya tetap.

c. GAS

Partikel-partikel gas sangat berjauhan, ikatan antara partikel sangat lemah sehingga

partikel-partikel gas mudah meninggalkan kelompoknya. Oleh sebab itu gas memiliki sifat bentuk dan

volumenya mudah berubah.

MASSA JENIS ( )

Massa jenis adalah massa benda tiap satuan volume. Sehingga untuk mengukur massa jenis zat maka kita dapat mengukur massa dan volume benda tersebut, kemudian menghitung massa dibagi dengan

volumenya. Untuk zat cair kita dapat juga mengukur massa jenis dengan menggunakan hidrometer.

TERAPUNG, MELAYANG DAN TENGGELAM TERAPUNG

Benda terapung dalam zat cair bila massa jenis benda lebih kecil dari massa jenis zat cair .

MELAYANG

Benda melayang dalam zat cair bila massa jenis benda sama dengan massa jenis zat cair.

TENGGELAM

Benda tenggelam dalam zat cair bila massa jenis benda lebih besar dari massa jenis zat cair.

V

m

ρ



BESARAN mks/SI cgs Massa (m) kg g Volume (V) m3 cm3 Massa jenis kg/m3 _g/cm3 N.B: 1 g/cm3 = 1.000 kg/m3 zatcair benda







zatcair benda







zatcair benda







Contoh Soal

1.Sebuah benda yang hendak ditentukan massa jenisnya, diukur melalui percobaan menimbang massanya dan mengukur volume yang hasilnya seperti pada gambar di bawah ini.

Berapa massa jenis benda benda ? Jawab

Melalui pembacaan neraca , massa benda 365 g Volume benda adalah 25 ml

Maka massa jenis benda

3 3 3

14

,

6

14

.

600

25

365

m

kg

cm

g

cm

g

V

m

ρ









INDIKATOR UN 2013

Konversi Suhu Pada Termometer Skala Termometer

C : R : F : K = 100 : 80 : 180 : 100 = 5 : 4 : 9 : 5 Contoh Soal

1. Suhu 25o C setara dengan = ... oR = ... oF = ... K R = 4/5 x 25o R = 20o R

F = 9/5 x 25 + 32o _{F = 45 + 32}o _{F = 77}o _F

K = 25 + 273 K = 298

2. Suhu50o F setara dengan = . . . oC = . . . 0R = . . . K C = 5/9 x ( 50 – 32)o C = 5/9 x 18o C = 10o C

= 4/9 x ( 50 – 32)o R = 4/9 x 18o R = 8o R = 5/9 x ( 50 – 32) + 273 K = 10 + 273 K = 283 K 3. Menentukan konversi suhu pada termometer.

R = 4/5 to _R F = 9/5 t + 32o F K = t + 273 K C = 5/4 to C F = 9/4 t + 32o F K = 5/4 t + 273 K C = 5/9 (t – 32)o _C R = 4/9 (t – 32)oR K = 5/9 (t – 32)+273 K C = t – 273 oC Diketahui dalam skala C Diketahui dalam skala F

Diketahui dalam skala R Diketahui dalam skala K

o_C 0 100 o_R 0 80 o_F 32 212 K 273 373 100sk 80sk 180sk 100sk

Untuk konversi suhu pada termometer dapat juga menggunakan rumus perbandingan sebagai berikut asal titik tetap bawah dan titik tetap atas masing-masing termometer diketahui.(lihat contoh di bawah)

Contoh Soal

1. Suhu 25o C setara dengan ... o F

INDIKATOR UN 2013

KALOR DAN PERUBAHAN SUHU

Kalor berperan pada perubahan suhu zat. Pada saat zat menerima kalor, maka suhu zat naik sebaliknya ketika zat melepaskan kalor maka suhu zat turun. Banyaknya kalor yang diserap dan kalor yang dilepaskan sehingga suhu zat berubah tergantung pada :

1. Kenaikkan / penurunan suhu

2. massa zat

3. jenis zat ( kalor jenis zat ) RUMUS :

4. Menentukan besaran kalor dalam proses perubahan suhu atau penerapan perubahan wujud zat dalam kehidupan sehari-hari.

dalam kehidupan sehari-hari.

Q = m x c x



t = m x c x (t

2

– t

1

)

X Y X1 Xo Yo Y1 X Y 4 5 80 100 0 80 0 0 100 0 R C R C R C        Celcius Reamur 100o 0o ₀o 80o C R Celcius Fahrenheit 100o 0o ₃₂o 212o C F

9

32

5

180

32

100

32

212

32

0

100

0



















F

C

F

C

F

C

0

1

0

0

1

0

Y

Y

Y

Y

X

X

X

X











Celcius Fahrenheit 100o 0o ₃₂o 212o 25o _F

9

32

5

25

9

32

5









F

F

C

F

o

F

F

F

77

32

45

45

32

9

32

5















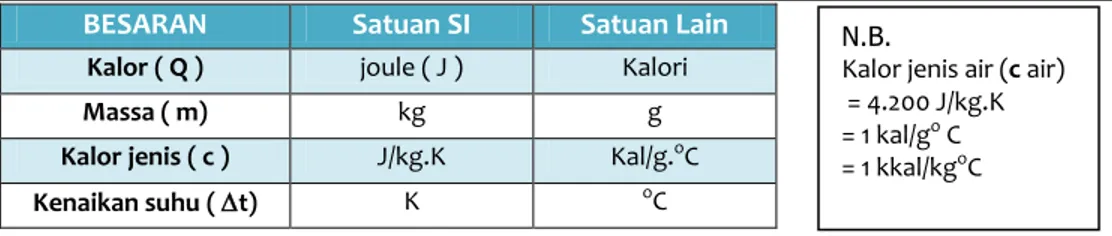
BESARAN Satuan SI Satuan Lain Kalor ( Q ) joule ( J ) Kalori

Massa ( m) kg g

Kalor jenis ( c ) J/kg.K Kal/g.o_C

Kenaikan suhu ( t) K oC

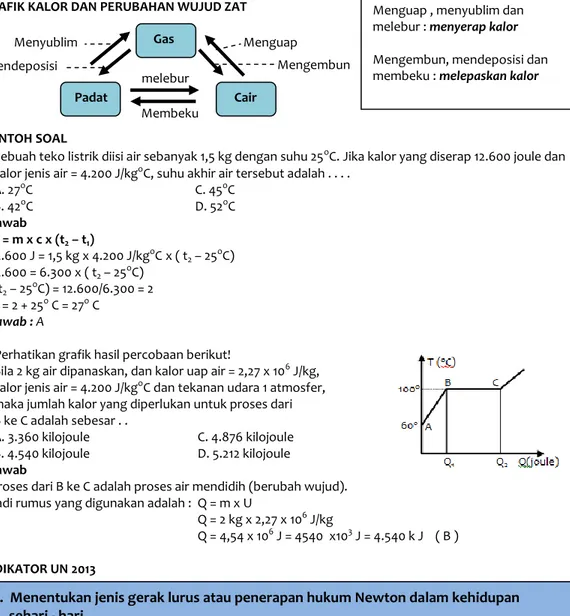
KALOR DAN PERUBAHAN WUJUD ZAT

Pada saat zat dipanaskan pada suhu tertentu suhu zat tidak berubah , zat menyerap kalor tetapi kalor yang

diserap dipakai untuk mengubah wujud zat . Demikian juga ketika zat melepaskan kalor , pada suhu

tertentu suhu zat tetap . Kalor yang dilepaskan digunakan untuk mengubah wujud zat. Suhu pada waktu zat berubah wujud disebut :

1. Titik lebur : suhu pada saat zat padat melebur ( berubah wujud dari padat menjadi cair) 2. Titik didih : suhu pada saat zat cair mendidih (berubah wujud dari cair menjadi gas ) 3. Titik beku : suhu pada saat zat cair membeku (berubah wujud dari cair menjadi padat ) 4. Titik embun : suhu pada saat gas mengembun (berubah wujud dari gas menjadi cair ) Kalor yang diperlukan/dilepaskan ketika zat berubah wujud tergantung pada :

1. Massa zat ( m )

2. Kalor lebur ( L )/ kalor Uap (U ) dari zat tersebut RUMUS :

GRAFIK SUHU - PERUBAHAN SUHU DAN PERUBAHAN WUJUD ES – AIR - UAP

BESARAN Satuan SI Satuan Lain Kalor ( Q ) joule ( J ) Kalori

Massa ( m) kg g

Kalor Lebur ( L) J/kg Kal/g Kalor Uap (U) J/Kg Kal/g

N.B.

Kalor jenis air (c air) = 4.200 J/kg.K = 1 kal/go C = 1 kkal/kgoC

Q = m X L

Q = m X U

Melebur/membeku Mendidih/mengembun 0O_C 100O_C -tO_C Suhu Kalor Q=m x ces x t Q=m x L Q=m x cair x t Q=m x U

GRAFIK KALOR DAN PERUBAHAN WUJUD ZAT

CONTOH SOAL

1. Sebuah teko listrik diisi air sebanyak 1,5 kg dengan suhu 25oC. Jika kalor yang diserap 12.600 joule dan

kalor jenis air = 4.200 J/kgoC, suhu akhir air tersebut adalah . . . .

A. 27oC C. 45oC B. 42oC D. 52oC Jawab Q = m x c x (t2 – t1) 12.600 J = 1,5 kg x 4.200 J/kgoC x ( t2 – 25oC) 12.600 = 6.300 x ( t2 – 25oC) ( t2 – 25oC) = 12.600/6.300 = 2 t2 = 2 + 25o C = 27o C Jawab : A

2. Perhatikan grafik hasil percobaan berikut!

Bila 2 kg air dipanaskan, dan kalor uap air = 2,27 x 106 _J/kg,

kalor jenis air = 4.200 J/kgoC dan tekanan udara 1 atmosfer,

maka jumlah kalor yang diperlukan untuk proses dari B ke C adalah sebesar . .

A. 3.360 kilojoule C. 4.876 kilojoule

B. 4.540 kilojoule D. 5.212 kilojoule

Jawab

Proses dari B ke C adalah proses air mendidih (berubah wujud). Jadi rumus yang digunakan adalah : Q = m x U

Q = 2 kg x 2,27 x 106 J/kg

Q = 4,54 x 106 _{J = 4540 x10}3 _{J = 4.540 k J ( B )} INDIKATOR UN 2013

GERAK LURUS

Gerak lurus terdiri dari :

1 . GERAK LURUS BERATURAN ( Gerak Lurus dengan kecepatan tetap)

2. GERAK LURUS BERUBAH BERATURAN ( Gerak Lurus dengan kecepatan berubah secara beraturan ) Menguap , menyublim dan

melebur : menyerap kalor

Mengembun, mendeposisi dan

membeku : melepaskan kalor

Gas Padat Cair Membeku Mengembun melebur Menguap Menyublim Mendeposisi

5. Menentukan jenis gerak lurus atau penerapan hukum Newton dalam kehidupan sehari - hari

GERAK LURUS BERATURAN (GLB)

Benda dikatakan bergerak lurus beraturan bila bergerak dengan lintasan lurus dan kecepatannya tetap. RUMUS GLB :

GRAFIK GLB

Jenis gerak Lurus dapat diamati dengan menggunakan ticker timer. Dengan memasang ticker timer maka benda benda yang bergerak lurus beraturan (GLB) tampak seperti gambar berikut :

GERAK LURUS BERUBAH BERATURAN (GLBB)

Benda dikatakan Bergerak Lurus Berubah Beraturan bila benda tersebut bergerak dengan lintasan lurus dan kecepatannya berubah secara beraturan.

GERAK LURUS BERUBAH BERATURAN terdiri dari : 1. Gerak Lurus Dipercepat Beraturan 2. Gerak Lurus Diperlambat Beraturan RUMUS :

GRAFIK GLBB

BESARAN SATUAN SI SATUAN LAIN

Jarak (S) m km , cm

Kecepatan (v) m/s km/jam, cm/s

Waktu (t) s Jam

BESARAN SATUAN SI SATUAN LAIN Kecepatan Awal (Vo ) m/s cm/s Kecepatan akhir (Vt) m/s cm/s Percepatan/perlambatan ( a) m/s2 cm/s2 Waktu ( t ) s s Jarak tempuh ( S ) m cm

S = v x t

v t 0 s t 0 0 s t

V

t

= V

o

± a.t

S = V

o.

t ± ½ a.t

2 O t v Dipercepat 0 s t Diperlambat s t Dipercepat t 0 O v Diperlambat

Jenis Gerak Lurus Berubah Beraturan bila dilihat dengan menggunakan ticker timer sebagai berikut :

Contoh Soal

1.Sebuah mobil mengalami kebocoran oli dan melakukan pengereman sehingga bergerak lurus berubah beraturan. Tetesan secara periodik pada jalan seperti gambar . . . .

A.

B.

C.

D.

2. Seorang anak meluncur maju di jalan seperti pada gambar berikut tanpa mengayuh pedal sepedanya.

Jenis gerak lurus berubah beraturan (GLBB) yang terjadi pada sepeda ketika melalui lintasan . . . .

A - B C - D A. GLBB dipercepat GLBB dipercepat B. GLBB diperlambat GLBB dipercepat C. GLBB diperlambat GLBB diperlambat D. GLBB dipercepat GLBB diperlambat Jawab : D ● ● ● ● ● ● ● ● ● ● ● ● ● ●  ● ● ● ● ● ● ●  ● ● ● ● ● ● ●  Jawab : C GERAK LURUS DIPERCEPAT

BERATURAN

GERAK LURUS DIPERLAMBAT BERATURAN

DUA BENDA BERGERAK LURUS BERATURAN DENGAN ARAH SALING BERLAWAN

Bila kedua mobil bergerak GLB dan bergerak bersamaan ,maka waktu tempuh kedua mobil ketika tabrakan adalah :

Contoh Soal

Mobil 1 bergerak GLB dari A ke B dengan kecepatan 3 m/s , sedangkan mobil 2 secara bersamaan bergerak GLB dari B ke A dengan kecepatan 2 m/s. Jika A dari B 600 m, tentukan

a. waktu kedua mobil ketika bertabrakan

b. jarak yang ditempuh mobil 1 ketika bertabrakan

Jawab a.

120s

2m/s

3m/s

600m

2

v

1

v

S

t











b. S1 = v1 x t1 = 3 m/s x 120 s = 360 m

DUA BENDA BERGERAK LURUS BERATURAN SALING MENYUSUL

Untuk benda yang bergerak saling menyusul , benda pertama bergerak lebih dahulu disusul oleh benda kedua yang memiliki kecepatan lebih besar agar dapat menyusul benda pertama. Mobil kedua akan menyusul mobil pertama dan pada saat itu jarak yang ditempuh kedua mobil sama. Ketika itu waktu

tempuh kedua mobil memiliki perbedaan waktu t .

Rumus :

S

1

V

1

V

2

S

2

S

t

2

v

1

v

S

t





S

1

= v

1

x t

S

2

= v

2

x t

V

1

V

2

S = S

1

= S

2

S

1

= S

2

V

1

x t

1

= V

2

x t

2

V

1

x t

1

= V

2

x (t

1

-



t )

HUKUM NEWTON

Ada 3 hukum Newton yang berhubungan dengan gerak : 1. HUKUM I NEWTON

Jika tidak ada gaya yang bekerja pada benda, maka benda yang diam akan tetap diam sedangkan benda yang sedang bergerak akan tepat bergerak dengan kecepatan konstan.

RUMUS :

Hukum I Newton sering juga disebut hukum kelembaman ( sifat malas pada benda) artinya bila benda

sedang diam ingin tetap mempertahankan kedudukannya yaitu tetap diam , sedangkan bila benda sedang

bergerak ingin tetap mempertahankan untuk tetap bergerak. Contoh : Pada saat penumpang dalam mobil

sedang diam dan kemudian tiba-tiba mobil bergerak maka badan penumpang akan terdorong ke arah belakang ( mempertahankan posisi diam). Sebaiknya pada saat penumpang berada dalam mobil yang sedang melaju kencang ( penumpang dalam mobil ikut bergerak) dan tiba-tiba mobil direm ( berhenti), maka si penumpang akan terdorong ke depan ( penumpang mempertahankan tetap bergerak ) 2. HUKUM II NEWTON

Jika ada resultan gaya yang bekerja pada benda , maka benda akan mengalami percepatan. RUMUS :

Contoh penerapan Hukum II Newton :

- Benda jatuh akan mengalami percepatan karena gaya tarik bumi.

- Benda yang dilemparkan vertikal ke atas akan mengalami perlambatan dan akhirnya pada titik tertinggi berhenti karena di tarik oleh gaya gravitasi bumi dengan arah yang berlawanan dengan arah geraknya.

Contoh Soal

Sebuah balok massanya 5 kg didorong dengan gaya seperti tampak pada gambar di bawah ini. Yang akan terjadi pada benda akibat gaya-gaya tersebut adalah . . . .

A. benda akan mengalami percepatan 6 m/s2 _{ke kanan}

B. benda akan mengalami percepatan 6 m/s2 ke kiri

C. benda tetap diam karena mempunyai sifat kelembaman D. benda akan bergerak dengan kecepatan konstan Jawab F = m x a ( F1 – F2 ) = m x a 50 N – 20 N = 5 kg x a 30 N = 5 kg x a a = 30N/5kg = 6 N/kg = 6 m/s2 _{( Jawab: A )}

3. HUKUM III NEWTON

Gaya aksi = - Gaya reaksi ( F aksi = - F reaksi )

Bila benda 1 memberikan gaya aksi pada benda 2 , maka benda 2 akan memberikan gaya reaksi pada benda 1 dengan besar gaya yang sama dengan arah yang berlawanan.

BESARAN SATUAN SI SATUAN LAIN

Gaya ( F ) newton ( N ) dyne

Massa ( m) kg g Percepatan ( a) m/s2 _{/ N/kg cm/s}2



F = 0



F = m x a

5 kg F1 = 50 N F2 = 20 N

Contoh : - Bila kaki kita menendang tembok dengan kuat ( gaya yang besar ), maka tembok akan memberikan gaya reaksi pada kaki dengan besar gaya yang sama sehingga kita merasakan kaki kita terasa lebih sakit dibandingkan dengan bila kita menendang dengan gaya kecil.

- Pada saat peluru ditembakkan dan keluar dari meriam, maka meriam akan terdorong ke arah belakang.

INDIKATOR UN 2013

Usaha dalah hasil kali gaya dengan perpindahan akibat gaya tersebut. RUMUS :

BESARAN SATUAN SI SATUAN LAIN

Gaya ( F ) , Berat ( w) newton ( N ) dyne

Perpindahan ( S ) , ( h ) m cm

Usaha ( W ) joule ( J ) erg

CONTOH SOAL

1. Usaha yang diperlukan untuk mengangkat benda yang massanya 20 kg setinggi

50 cm pada gambar di atas adalah . . . . ( g = 10 m/s2 ₎

Jawab :

W = w x h = m x g x h W = 2 kg x 10 m/s2 x 0,5 m W = 10 joule .

2. Berapa usaha yang diperlukan untuk memindahkan benda dengan gaya 25 N sejauh 40 cm seperti pada gambar di bawah ini ?

Jawab : W = F x S W = 25 N x 0,4 m W = 10 joule

6. Menentukan besaran fisis pada usaha atau energi .

W = F x S

F

S

W = w x h

W

F

h

W = mg x h

F _{50 cm} 20kg

25 N

40 cm

ENERGI POTENSIAL GRAVITASI , ENERGI KINETIK DAN ENERGI MEKANIK Energi adalah kemampuan untuk melakukan usaha

Energi Potensial Gravitasi ( Ep) : energi yang dimiliki benda karena kedudukannya terhadap acuan tertentu. RUMUS :

Energi Kinetik ( Ek) : energi yang dimiliki yang benda yang bergerak

Energi Mekanik (Em) : Gabungan energi potensial dan energi kinetik yang dimiki benda. Energi mekanik yang dimiliki benda selalu tetap karena berlaku hokum kekekalan energi.

HUKUM KEKEKALAN ENERGI MEKANIK

Contoh Soal

1. Sebuah bola basket massanya 2 kg jatuh dari ketinggian 5 m dari tanah.

Bila percepatan gravitasi 10 m/s2, maka tentukan

a) Energi potensial bola mula-mula

b) Energi kinetik bola ketika mengenai lantai

Jawab

a. Ep = m x g x h

Ep = 2 kg x 10 m/s2 x 5 m Ep = 100 joule

b. Gunakan hukum kekekalan energi mekanik karena energi mekanik bola tetap. Ep1 + Ek1 = Ep2 + Ek2

100 joule + 0 = 0 + Ek2

Jadi Ek bola ketika mengenai lantai (Ek2 ) = Ep1 = 100 joule. BESARAN SATUAN SI SATUAN LAIN

Energi Potensial (Ep) Joule ( J ) erg

Energi Kinetik ( Ek ) Joule ( J ) erg

Massa ( m ) kg g Ketinggian ( h ) m cm Kecepatan ( v ) m/s cm/s h

Ep = m x g x h

_{Ek = ½ m x v}

2 v

Em = Ep + Ek

Ep

1

+ Ek

1

= Ep

2

+ Ek

2

2. Sebuah sepeda massanya 15 kg bergerak dengan kecepatan 2 m/s. Berapa besar energi kinetik sepeda saat itu ?

Jawab Ek = ½ .m.v2

Ek = ½ . 15 kg . (2m/s)2 Ek = ½ . 15 . 4 joule = 30 joule. INDIKATOR UN 2013

Pesawat Sederhana adalah alat yang digunakan untuk memudahkan melakukan usaha. TIGA JENIS PESAWAT SEDERHANA :

1. TUAS / PENGUNGKIT

2. KATROL ( Katrol tetap , katrol bergerak , sistem katrol) 3. BIDANG MIRING

1. TUAS/PENGUNGKIT

CONTOH ALAT-ALAT YANG BEKERJA BERDASARKAN PRINSIP TUAS

TUAS - Tuas Kelas 1.

Yang dimaksud tua kelas 1 adalah tuas yang bekerja dengan titik tumpu (T) berada di tengah-tengah.

- Tuas Kelas 2.

Yang dimaksud tuas kelas 2 adalah tuas yang bekerja dengan beban ( B/W ) berada di tengah-tengah.

- Tuas Kelas 3

Yang dimaksud tuas kelas 2 adalah tuas yang bekerja dengan kuasa ( K/F ) berada di tengah-tengah.

Untuk mudah mengingat hafalkan saja : TBK ( secara berurutan tuas kelas 1 : T di tengah, tuas kelas 2 : B di

tengah dan tuas kelas 3 : K di tengah )

7. Menentukan penerapan pesawat sederhana dalam kehidupan sehari-hari.

Lb

Lk

F

W

KM





W x Lb = F x Lk

W = berat beban F = Gaya / Kuasa Lb = lengan beban Lk = lengan kuasa KM = Keuntungan mekanik

Contoh Tuas

2. KATROL

Katrol terdiri dari : Katrol tetap , katrol bergerak dan system katrol

2.1. KATROL TETAP

Katrol tetap : memiliki keuntungan merubah arah gaya sehingga mudah melakukannya , keuntungan mekanik katrol tetap KM = 1 ( Gaya yang dikeluarkan sama dengan berat beban(W) yang harus diangkat). KM adalah perbandingan dari beban (W) dengan gaya (F) yang dikeluarkan. Makin besar KM pesawat , makin untung / mudah kita melakukannya , karena makin kecil gaya yang harus dikeluarkan.

RUMUS

2.2. KATROL BERGERAK

Katrol bergerak : memiliki Keuntungan Mekanik KM = 2. Ini berarti gaya yang harus dikeluarkan F = ½ W dari berat beban W yang harus diangkat.

RUMUS

BESARAN SATUAN SI Berat Benda ( W ) newton (N) Gaya / Kuasa ( F ) newton(N) Keuntungan Mekanik ( KM) -

1





F

W

KM

F = W

2





F

W

KM

F = ½ W

2.3. SISTEM KATROL

Sistem Katrol : Keuntungan mekanik dari sistem katrol tergantung dari jumlah katrol yang dipasang serta bagaimana menyusunnya. Sebagai contoh sistem katrol di bawah ini terdiri dari 2 katrol 1 katrol tetap dan 1 katrol bergerak . Sistem katrol ini memiliki keuntungan mekanik 2. Keuntungan mekanik sama dengan jumlah tali yang menahan beban.

3. BIDANG MIRING

Bidang Miring : Keuntungan mekanik bidang miring tergantung pada panjang bidang miring dan ketinggiannya ketika digunakan.

RUMUS :

CONTOH ALAT-ALAT YANG BEKERJA BERDASARKAN BIDANG MIRING BESARAN SATUAN SI

Berat Benda ( W ) newton (N)

Gaya / Kuasa ( F ) newton(N)

Keuntungan Mekanik ( KM) - Panjang Bidang ( L) m Tinggi bidang (h) m 1 2

KM = 2

F = ½ W

KM = 4

_{F = ½ W}

h

L

F

W

KM





L

h

W

F

Contoh Soal

1. Berapa besar gaya yang diperlukan untuk mengangkat benda yang beratnya 200 N bila

menggunakan

2. Perhatikan permainan jungkat-jungkit seperti gambar berikut !

Massa anak A lebih berat dari anak B. Agar terjadi keseimbangan pada jungkat-jungkit, maka posisi yang benar adalah . . . .

A. titik tumpu T digeser ke titik P B. anak B bergeser ke titik R C. anak A bergeser ke titik P D. anak B bergeser ke titik Q

Jawab : C.

Agar seimbang, maka anak yang lebih berat posisinya lebih dekat dari titik tumpu atau anak yang lebih ringan posisinya harus lebih jauh dari titik tumpu.

a. Katrol tetap Jawab KM = 1 jadi F = W F = 200 N b. Katrol bergerak Jawab KM = 2 jadi F = ½ W F = ½ x 200 N = 100 N

c. Bidang miring seperti gambar

Jawab

2m

5m

F

200N

_





h

L

F

W

KM

F x 5m = 200 N x 2 m F = 400 Nm/5m F = 80 N

F

W=200N W=200N

F

F

W=200N 5 m 2 m

INDIKATOR UN 2013

TEKANAN

Tekanan adalah : Gaya yang bekerja pada benda tiap satuan luas. RUMUS :

 TEKANAN PADA BIDANG (Zat Padat )

Contoh Soal

1. Sebuah kardus yang berisi mangga mempunyai massa 24 kg terletak di atas lantai dan ukurannya seperti

pada gambar (g = 10m/s2). Besar tekanan kardus terhadap lantai adalah . . . .

A. 600 N/m2 B. 1000 N/m2 C. 1200 N/m2 D. 2400 N/m2 Jawab : A

_m2 N 600 2 0,4m 240N 2 m N 0,4 1 10 24 A g m A F P        

2. Sebuah balok massanya 5 kg berukuran 20 cm x 10 cm x 5cm seperti pada gambar .

Bila percepatan gravitasi g = 10 m/s2 _{, tekanan maksimum balok pada alasnya pada lantai}

adalah . . . . A. 15.000 Pa B. 10.000 Pa C. 5.000 Pa D. 2.500 Pa Jawab : B

BESARAN SATUAN SI SATUAN LAIN

Gaya (F)/Berat(W) newton(N) dyne

Luas alas ( A ) m2 cm2

Tekanan ( P ) N/m2 = Pa dyne/cm2 8. Menentukan besaran fisis yang terkait dengan tekanan pada suatu zat.

A

F

P



A W

A

g

m

A

W

A

F

P









min

A

F

maks

P



maks

A

F

min

P



20 cm 10 cm 5 cm 1 m 0,4 m 0,6 m

A

min

F

maks

P



10.000Pa 2 0,005m 50N 0,05m 0,1m 2 10m/s 5kg min A F maks P      

TEKANAN HIDROSTATIK ( Tekanan Pada Zat Cair )

Tekanan Hidrostatik adalah : Tekanan dalam zat cair yang diam.

CONTOH SOAL

Seekor ikan berada pada bak air seperti pada gambar.

Jika massa jenis air = 1.000 kg/m3 dan percepatan gravitasi 10 N/kg,

tekanan hidrostatis yang diterima ikan di titik Q adalah . . . .

A. 6.000 N/m2 B. 8.000 N/m2 C. 10.000 N/m2 D. 14.000 N/m2 Jawab : B h = 80 cm = 0,8 m Ph =  x g x h Ph = 1.000 kg/m3 x 10 m/s2 x 0,8 m = 8.000 N/m2  HUKUM PASCAL

Hukum Pascal : Tekanan dalam zat cair diteruskan ke segala arah sama rata.

Alat-alat yang bekerja berdasarkan Hukum Pascal 1. Dongkrak Hidrolik

2. Pesawat Pengangkat Mobil 3. Kursi Pasien Dokter Gigi 4. Jarum Suntik Air 80 8 0 cm Q 80 ₆ 0 cm

Contoh Soal

Sebuah mobil yang massanya 1.200 kg diangkat dengan menggunakan hidrolik seperti ditunjukkan pada

gambar di atas (g = 10 m/s2_{).Luas penampang penghisap kecil 0,2 m}2 _{, luas penampang penghisap besar 4}

m2. Besar gaya F pada penghisap kecil yang diperlukan agar dapat mengangkat mobil tersebut adalah . . . .

A. 300 N C. 240 N B. 250 N D. 200 N Jawab : 2 A W 1 A 1 F  2 m 4 2 10m/s 1.200kg 2 0,2m F   4 F = 0,2 x 12.000 N F = 600 N INDIKATOR UN 2013 1. GETARAN

Getaran adalah : Gerak bolak balik di sekitar titik keseimbangan. Periode ( T ) : Waktu yang diperlukan untuk melakukan 1 getaran Frekuensi ( f) : Jumlah getaran tiap detik

Amplitudo ( A ) : Simpangan maksimum RUMUS :

Contoh Soal

1. Sebuah bola berayun dari A – B – C selama 0,5 sekon dan jarak A – C = 12 cm. Frekuensi dan amplitudo

ayunan adalah . . . . A. 0,5 Hz dan 6 cm B. 0,5 Hz dan 12 cm C. 1 Hz dan 6 cm D. 1 Hz dan 12 cm Jawab : C t = 0,5 sekon n = ½ getaran ( A – B – C ) Hz 1Hz 0,5 0,5 t n f    BESARAN SATUAN SI Jumlah getaran ( n ) - Waktu (t) s Periode ( T ) s Frekuensi ( f) Hz

9. Menentukan besaran fisis pada getaran atau gelombang. A p _q r 1 getaran : . p – q – r – q – p . r – q – p – q – r . q – r – q – p – q

n

t

T



t

n

f



f

1

T



 A B C A – C = 12 cm = 2 x amplitudo Jadi ampltudo = 12 cm/2 = 6 cm .

2. Pada sebuah benda yang bergetar , untuk bergerak dari P – q – r – q diperlukan waktu 1,5 s. Tentukan periode dan frekuensi gelombang ! Jawab P – q – r – q  n = ¾ t = 1,5 s

2s

3

4

1,5s

4

3

1,5s

n

t

T











Hz

2

1

3

2

4

3

1,5s

4

3

t

n

f











2. GELOMBANG

Gelombang adalah : Getaran yang merambat.

 Gelombang Transversal : Gelombang yang arah getarnya tegak lurus terhadap arah perambatannya. Gelombang Longitudinal : Gelombang yang arah getarnya sejajar dengan arah perambatannya.

Contoh Soal

3. Perhatikan grafik simpangan gelombang terhadap waktu pada gambar berikut !

Tentukan a) ampitudo gelombang d) periode gelombang

b) panjang gelombang e) cepat rambat gelombang

c) frekuensi gelombang

Gelombang Transversal Gelombang Longitudinal Atau P – q – r – q 

T

1,5s

4

3



2s

3

4

1,5s

T







Hz

2

1

T

1

f





A B cm 0 0,5 1,0 1,5 2,0 1 0 2 0 -10 -20 Waktu(s) 250 cm 5cm

Jawab ( lihat gambar ) a) Amplitudo gelombang = 5 cm b) 1 ¼  = 250 cm  = 250 cm : 5/4  = 250 cm x 4/5  = 200 cm

Jadi panjang gelombang  = 200 cm.

c) Periode ( T ) = 2 s f = 1/T = ½ Hz

Jadi frekuensi gelombang ( f ) = ½ Hz. d) Periode ( T ) = 2 s

e) v = f x  = ½ Hz x 200 cm = 100 cm/s. Atau v = /T = 200cm/2s = 100 cm/s

Jadi cepat rambat gelombang (v) = 100 cm/s INDIKATOR UN 2013

BUNYI

Sifat-sifat dari gelombang bunyi

1. Bentuk gelombang longitudinal

2. Untuk merambat bunyi memerlukan medium

3. Bunyi merambat paling cepat berturut –turut mulai dari zat padat , zat cair dan gas

4. Bunyi dapat didengar oleh manusia (bunyi audio) bila memiliki frekuensi 20 Hz  f  20.000 Hz

Frekuensi bunyi < 20 Hz disebut : infrasonik

Frekuensi bunyi > 20.000 Hz (20 kHz) disebut : ultrasonik

5. Bunyi dapat dipantulkan , dibiaskan.

Pemanfaat bunyi pantul untuk menentukan kedalaman laut, USG untuk mengamati janin ibu yang hamil.

6. Bunyi terdengar keras bila memiliki amplitudo yang besar

Bunyi terdengar tinggi bila memiliki frekuensi besar

CEPAT RAMBAT BUNYI RUMUS :

MENGUKUR KEDALAMAN LAUT / JARAK PEMANTUL DENGAN GEMA

BESARAN SATUAN SI

Cepat rambat ( v ) m/s

Kedalaman ( h ) / Jarak pemantul ( S) m

Waktu ( t) s

10. Menjelaskan sifat bunyi atau penerapannya dalam kehidupan sehari-hari.

S = v x t

h

2h = v x t

2

t

v

h





Contoh Soal

1. Seorang anak berteriak sambil menghadap tebing yang ada di depannya. Setelah 4 detik terdengar bunyi ulangnya. Jika cepat rambat bunyi di udara saat itu 320 m/s, maka jarak anak dari tebing adalah . . . .

A. 1.280 m C. 640 m B. 960 m D. 80 m Jawab : B t = 4 s v = 320 m/s

640m

m

2

4

320



_







2

t

v

s

2. Sebuah bel listrik dibunyikan di dalam selinder kaca tertutup. Kemudian udara dari dalam silinder

dipompa keluar sedikit demi sedikit hingga habis. Bunyi bel terdengar makin lemah dan akhirnya tidak terdengar. Peristiwa ini terjadi karena . . . .

A. bunyi merambat memerlukan medium C. bunyi terbawa keluar bersama kaca

B. bunyi diredam oleh bahan kaca D. frekuensi bunyi bel di bawah 20 Hz

Jawab : A NADA

Nada adalah : Bunyi yang frekuensinya teratur

Desah : Bunyi yang frekuensinya tidak teratur. ( angin , ledakan bom , kaca pecah dsb) Interval nada: Perbandingan frekuensi nada-nada.

c : d : e : f : g : a : b : c1 24 : 27 : 30 : 32 : 36 : 40 : 45 : 48

Nada Standar : a = 440 Hz.

Interval nada-nada penting

1 : 2 : 3 : 4 : 5

RESONANSI

Resonansi adalah : Peristiwa ikut bergetarnya sebuah benda karena getaran benda lain. Keuntungan Resonansi

Resonansi dapat memperkuat bunyi asli seperti yang terjadi pada alat-alat musik Kerugian Resonansi

Akibat resonansi gedung , jembatan dapat rubuh. MANFAAT GELOMBANG BUNYI

1. Dapat digunakan untuk mengukur kedalaman laut disini yang digunakan adalah bunyi ultrasonik 2. Mendeteksi janin dalam rahim, biasanya menggunakan bunyi infrasonik

3. Mendeteksi keretakan suatu logam dan lain-lain.

4. Diciptakannya speaker termasuk manfaat dari bunyi audiosonik. Oktaf Kuint Kuart Terts

INDIKATOR UN 2013

Sifat – sifat Cahaya :

1. Cahaya merambat menurut garis lurus ( terbentuk bayang-bayang di belakang benda gelap)

2. Cahaya tidak memerlukan medium untuk merambat (termasuk gelombang elektromagnetik ) dan cepat

rambat cahaya dalam ruang hampa c = 3 x 108 _m/s

3. Bentuk gelombang cahaya : Transversal

4. Cahaya dapat dipantulkan ( membentuk bayangan pada cermin ) dan dibiaskan ( membentuk bayangan pada lensa)

CERMIN CERMIN DATAR

Sifat bayangan yang dibentuk cermin datar :

- Maya , tegak , sama besar , di belakang cermin

- Jarak benda ke cermin sama dengan jarak bayangan ke cermin

- Untuk dapat melihat seluruh bayangan di cermin datar diperlukan tinggi

tinggi cermin ½ x tinggi badan. Bayangan yang dibentuk 2 cermin datar

CERMIN CEKUNG

Lukisan bayangan cermin cekung

Jarak fokus cermin cekung (+) karena berada di depan cermin. S1(+) : di depan cermin (bayangan nyata)

S1 (-) : di belakang cermin (bayangan maya) Teori Ruang Pada Cermin Cekung

Keterangan: So = Jarak benda

Si = Jarak bayangan

f = Jarak fokus cermin

R = jari-jari kelengkungan cermin ho = Tinggi benda hi = Tinggi bayangan M = Perbesaran bayangan

)

(positif

f

R

2

1

f

o

h

i

h

o

S

i

S

M

i

S

1

o

S

1

f

1















11. Menentukan sifat cahaya, besaran-besaran yang berhubungan dengan cermin / lensa atau penerapan alat optik dalam kehidupan sehari-hari.



_α

1

360

n







Si   O _{F P} So ho hi 1 2

Ruang benda + Ruang Bayangan = 5  So di R 1  Si di R 4

 So di R 2  Si di R 3  So di R 2½  Si di R 2½  So di R 3  Si di R 2 Jika

 Si = So  M = 1 (bayangan sama besar)

 Si  So  M  1 (bayangan diperbesar)  Si  So  M  1 (bayangan diperkecil)   R 1 R 2 R 3 R 4 R 2½ O _{F P}

 = sudut antara cermin

Contoh Soal

1. Sebuah benda diletakkan di depan cermin cekung seperti gambar, ternyata terbentuk bayangan pada

jarak S1 _{= 30 cm. Apabila letak benda bergeser mendekati cermin cekung sejauh 3 cm dari posisi semula,}

maka jarak bayangan dari cermin cekung sekarang adalah . . . . A. 40 cm B. 45 cm C. 50 cm D. 60 cm Jawab : D So = 15 cm Si = 30 cm 10cm 3 30 f 30 3 30 1 30 2 30 1 15 1 i S 1 o S 1 f 1         

Jarak benda So menjadi : 15 cm – 3 cm = 12 cm i S 1 o S 1 f 1   i S 1 12 1 10 1   i S 1 12 1 10 1   i S 1 60 1  Si = 60 cm

2. Sebuah benda berada 8 cm di depan cermin cekung yang jarak fokusnya 6 cm. Tentukan a. Jarak bayangan b. sifat bayangan c. perbesaran bayangan Jawab a. So = 8 cm f = 6 cm

24

1

24

3

24

4

8

1

6

1

s

1

f

1

s

1

f

1

s

1

s

1

o i i o



















Si = 24 cm

b. Untuk menentukan sifat bayangan dapat menggunakan teori ruang sbb : Benda di R 2 jadi bayangan ada di R 3

Sifat bayangan : Nyata , terbalik , di depan cermin , di perbesar

Atau bisa kita tentukan dengan menggambar bayangannya seperti pada gambar di atas. c. Perbesaran Bayangan







3



8cm

24cm

o

s

i

s

M

O F P   benda bayangan f M Cermin Benda s 15 cm

CERMIN CEMBUNG

Sifat Bayangan Cermin Cembung :

- Maya , tegak , diperkecil , di belakang cermin

Lukisan Bayangan Pada Cermin Cembung

Contoh Soal

Sebuah benda tingginya 2 cm berada pada jarak 4 cm di depan cermin cembung yang memiliki jari-jari kelengkungan 6 cm. Tentukan a. jarak bayangan b. sifat bayangan c. tinggi bayangan Jawab ho = 2 cm So = 4 cm

R = 6 cm jadi f = -1/2 R = - 3 cm ( ada di belakang cermin) a.

f

1

i

s

1

o

s

1





o

s

1

f

1

i

s

1





12

7

12

3

12

4

_

_

_











4

1

3

1

i

s

1

cm

7

5

1

cm

7

12

i

s









b. Sifat bayangan yang dibentuk cermin cembung selalu :

Maya , tegak, diperkecil, di belakang cermin. ( Lihat juga gambar ) c.

o

h

i

h

o

s

i

s



2cm

i

h

4cm

12/7cm



(negatif)

f

1/2R

f

o

h

i

h

o

S

i

S

M

i

S

1

o

S

1

f

1















  O F P 6 cm 4 cm 4 hi = 2 x 12/7 cm = 24/7 cm hi = 24/7 cm : 4 = 6/7 cm

LENSA

1. Lensa cembung (Konveks, konvergen) 2. Lensa cekung (Konkaf, divergen) LENSA CEMBUNG

Jarak fokus lensa cembung (f) = + Bayangan nyata: di belakang lensa. Bayangan maya: di depan lensa. (R.4) Teori Ruang Pada Lensa Cembung

Contoh Soal

Sebuah benda tingginya 2 cm berada pada jarak 4 cm di depan lensa cembung yang jarak fokusnya 3 cm. Tentukan a. jarak bayangan b. sifat bayangan c. perbesaran bayangan d. tinggi bayangan Jawab a. ho = 2 cm so = 4 cm f = 3 cm

o

s

1

f

1

i

s

1





12

1

12

3

12

4

4

1

3

1

i

s

1











Si = 12 cm

b.Berdasarkan gambar sifat bayangan : Nyata, terbalik, di belakang lensa, diperbesar

Atau berdasarkan teori ruang : So di R- 2 , maka Si di R- 3 , maka sifat bayangan : Nyata, terbalik, di belakang lensa , diperbesar.

o

h

i

h

o

S

i

S

M

i

S

1

o

S

1

f

1









+ 1 2 3 So _Si + R1 R2 2F1 F1 o F2 2F2 R. benda R3 R1 R2 R3 R. bayangan R4 bayangan

Ruang benda + Ruang Bayangan = 5  So di R 1  Si di R 4

 So di R 2  Si di R 3  So di R 2½  Si di R 2½  So di R 3  Si di R 2 Jika

 Si = So  M = 1 (bayangan sama besar)

 Si  So  M  1 (bayangan diperbesar)  Si  So  M  1 (bayangan diperkecil)

+

2F F O F 2F 4 cm

c.







3



4

12

o

s

i

s

M

Jadi perbesaran bayangan : 3 x

d.

o

h

i

h

M



hi = M x ho = 3 x 2 cm = 6 cm Jadi tinggi bayangan : 6 cm LENSA CEKUNG

Lensa Cekung selalu menghasilkan bayangan : Maya , tegak , di depan lensa, diperkecil.

Pembentukan Bayangan Pada Lensa Cekung

Jarak fokus lensa cekung (f):  KEKUATAN LENSA

Kekuatan lensa: Kemampuan lensa memfokuskan sinar-sinar. RUMUS:

Contoh Soal

1. Sebuah lensa cembung memiliki jarak fokus 25 cm. Kekuatan lensa tersebut adalah . . . .

A. 4 dioptri C. – 4 dioptri

B. 2 dioptri D. – 2 dioptri

Jawab : A

Ingat jarak fokus lensa cembung +

D 4D 25 100 





f

100

P

f

1

P



P = kekuatan lensa dalam satuan dioptri (D) f = Jarak fokus dalam satuan meter.

f

100

P



f = jarak fokus dalam satuan cm

o

h

i

h

o

S

i

S

M

i

S

1

o

S

1

f

1









 1 O F1 F2 Si So 2 3

ALAT OPTIK

 Mata  Mikroskop

 Kamera  Teleskop

 Lup  Periskop

MATA

1.Mata Normal (Emetrop)  Titik Dekat Mata (PP) =  25 cm

 Titik Jauh Mata (PR) di jauh tak terhingga ().

2.Mata Rabun jauh (Miopi)

 Titik Dekat Mata (PP)=  25 cm

 Titik Jauh Mata (PR) < 

 Bila melihat jauh bayangan jatuh di depan retina.

 Dibantu dengan kacamata lensa cekung

 Penyebab: - Bola mata terlalu lonjong

- Daya akomodasi mata sudah berkurang

RUMUS MIOPI

CONTOH SOAL

Seorang penderita miopi memiliki titik jauh mata 5 m. Agar dapat melihat benda jauh dengan jelas , berapa kekuatan lensa kacamata yang harus digunakan ?

Jawab PR = 5 m f = - PR = - 5 m

0,2D

D

5

1

f

1

P











3.Mata Rabun Dekat (Hipermetropi)  Titik dekat Mata (PP) > 25 cm

 Titik Jauh Mata (PR) normal = 

 Bila melihat pada jarak baca normal (25 cm)

bayangan jatuh di belakang retina.

 Dibantu dengan kacamata lensa cembung

 Penyebab: Bola mata terlalu pipih dan

daya akomodasi mata sudah berkurang. RUMUS HIPERMETROPI

f = jarak fokus lensa kacamata. PR = Titik jauh mata miopi.

25

PP

PP

25

f







f = jarak fokus lensa kacamata. PP= Titik jauh mata hipermetropi. f = - PR

Mata Normal melihat benda jauh

25 cm

retina

Mata Normal melihat benda dekat

Mata Miopi melihat benda jauh

4.Mata Tua ( Presbiopi )

 Tidak dapat melihat dekat dan jauh dengan jelas.

 Titik dekat mata (PP) > 25 cm  Titik jauh mata (PR) < 

 Dibantu dengan kacamata lensa rangkap (bifokal)

 Penyebab: Daya akomodasi mata sudah berkurang.

KAMERA

Aperture: Lubang/celah jalan masuknya cahaya. (Pada mata: pupil)

Diafragma: Berfungsi mengatur aperture (Pada mata: iris). Aperture besar, angka diafragma kecil.

Film: layar yang peka terhadap cahaya berfungsi untuk menangkap bayangan. (Pada mata: retina)

Bayangan Kamera : Nyata, terbalik, diperkecil di Film.

LUP (Kaca Pembesar) 1.Mata tidak berakomodasi

 Perbesaran bayangan yang dihasilkan minimum.

Untuk pengamatan dengan mata tidak berakomodasi , maka benda berada di titik fokus Lup.

2.Mata berakomodasi maksimum

 Perbesaran bayangan yang dihasilkan maksimum

Diafragma Aperture

i

S

1

o

S

1

f

1





F = Jarak fokus lensa So = jarak benda

Si = Jarak bayangan/jarak film dari lensa.

f

PP

min

M



Mmin = Perbesaran bayangan minimum. PP =Titik dekat mata.

Mata Normal PP = 25 cm. f = Jarak fokus lensa lup

So

Si

Film

Mata tidak berakomodasi : Benda berada di titik F lup. F1

So = f

Mmaks = perbesaran maksimum.

So = Jarak benda saat mata mengamati dengan berakomodasi maksimum. PP = Titik dekat mata.

f = Jarak fokus lensa lup

1

f

PP

maks

Untuk pengamatan dengan mata berakomodasi maksimum, benda berada di antara O dan F ( di R 1).

MIKROSKOP

Terdiri dari 2 buah lensa cembung.

1. Lensa Objektif : Lensa dekat objek yang akan dilihat

Lensa Objektif membentuk bayangan Nyata, terbalik, diperbesar.

2. Lensa Okuler : Lensa dekat mata

Lensa Okuler membentuk bayangan Maya, tegak, diperbesar

Bayangan Akhir Mikroskop

Mikroskop menghasilkan bayangan akhir : Maya, terbalik, diperbesar

Perbesaran Total MTotal = Mob  Mok.

Pengamatan dengan mikroskop dapat dilakukan 2 cara :

1. Mata Tidak berakomodasi ( Perbesaran minimum , mata tidak cepat lelah ) 2. Mata Berakomodasi Maksimum ( Perbesaran maksimum , mata cepat lelah )

TELESKOP (TEROPONG) Teropong Bintang.

Teropong bintang memiliki 2 lensa cembung yaitu objektif dan okuler. Umumnya dengan teropong pengamatan dilakukan dengan

mata tidak berakomodasi.

Perbesaran bayangan teropong bintang

M = perbesaran teropong bintang

Bayangan Akhir teropong bintang

Bayangan akhir teropong bintang: Maya, terbalik, diperbesar.

ok

f

ob

f

M



Mata berakomodasi maksimum : Benda berada di antara O dan F lup. F1

So <f

Si =25 cm

INDIKATOR UN 2013

LISTRIK STATIK (ELEKTROSTATIK) TEORI ATOM

Atom netral: jumlah proton dalam inti atom sama dengan jumlah elektron yang mengelilingi inti.

Atom bermuatan listrik negatif (Ion -): Jumlah elektron dalam atom lebih banyak dari jumlah proton dalam inti. (Elektron masuk ke atom)

Atom bermuatan listrik positif (Ion +): Jumlah elektron dalam atom lebih sedikit dari jumlah proton dalam inti. (Elektron pindah ke atom lain)

MEMBERI MUATAN LISTRIK PADA BENDA 1. Menggosok ( Bahan Isolator )

Mistar plastik digosok dengan kain wol menjadi bermuatan listrik negatif karena elektron dari wol berpindah ke mistar sebaliknya wol menjadi bermuatan listrik positif karena elektronnya berpindah ke mistar.

Kaca yang digosok dengan kain sutera menjadi bermuatan listrik positif karena elektron dari kaca

berpindah ke sutera, sebaliknya sutera menjadi bermuatan listrik negatif.

2.Induksi ( Bahan Konduktor )

Memberi muatan dengan caraInduksi adalah : Memberi muatan pada benda dengan cara mendekatkan

benda bermuatan listrik ke benda yang tidak bermuatan. Muatan listrik yang dihasilkan dengan cara

induksi selalu berlawanan jenis dengan muatan sumbernya. ELEKTROSKOP:

Elektroskop adalah : Alat untuk menyelidiki benda bermuatan listrik atau tidak. Bila benda bermuatan listrik Disentuhkan / didekatkan pada elektroskop, maka daun elektroskop akan mengembang.

12.

Menjelaskan gejala listrik statis dalam penerapan kehidupan sehari-hari.

Plastik bermuatan listrik negatif setelah digosok dengan kain wol dapat menarik potongan kertas Kaca/perspek menjadi bermuatan listrik positif setelah digosok dengan kain sutra. _ + + + + + _ _ _ _ _ _ + + + + + _ _ _ _ _ + +

INTERAKSI BENDA BERMUATAN LISTRIK

1. Muatan listrik yang sejenis akan saling menolak. (+ dgn +) ( dgn )

2. Muatan listrik yang berbeda jenis akan saling menarik. (+ dgn )

HUKUM COULOMB

Gaya tarik menarik/tolak menolak antara benda bermuatan listrik berbanding lurus dengan besar muatannya masing-masing dan berbanding terbalik dengan kuadrat jarak antara muatannya.

Contoh Soal

1. Perhatikan gambar penggaris plastik digosok dengan kain wol berikut !

Setelah penggaris plastik digosok dengan kain wol, maka aliran elektron dan muatan yang terjadi pada penggaris plastik adalah . . .

Jawab : D + + – –- + – r r r F F F F F F q1 q2 q1 q1 q2 q2 2 2 1

r

q

q

k

F





BESARAN SATUAN S.I. SATUAN LAIN

Muatan listrik (q) Coulomb (C) statcoulomb(Stc)

Jarak muatan (r) m cm

Konstanta (k) 9.109 _N.m2_/C2 _1dyne.cm2_/Stc2

Gaya listrik (F) newton (N) dyne

Kain wol Penggaris

INDIKATOR UN 2013

ARUS LISTRIK

Arus listrik: dianggap sebagai aliran muatan listrik positif (+) dari potensial tinggi ke potensial rendah.

Elektron () mengalir dari potensial rendah ke potensial tinggi.

KUAT ARUS LISTRIK

Kuat arus listrik: Muatan listrik yang mengalir tiap detik.

AMPEREMETER

Amperemeter: alat untuk mengukur kuat arus listrik dalam rangkaian listrik.

Amperemeter dirangkaikan secara seri.

VOLTMETER

Voltmeter: Alat untuk mengukur beda potensial/tegangan listrik.

Voltmeter dipasang secara paralel.

t

Q

I



Q = I . t

BESARAN SATUAN S.I.

Muatan Listrik (Q) coulomb (C) Waktu (t) sekon (s) Kuat Arus Listrik (I) ampere (A)

V Lambang Voltmeter V V V + – + – + – + –

13.Menentukan besaran-besaran listrik dinamis dalam suatu rangkaian (seri/paralel, Hukum Ohm, Hukum Kirchhoff) serta penerapannya dalam kehidupan sehari-hari.

Lambang Amperemeter

A

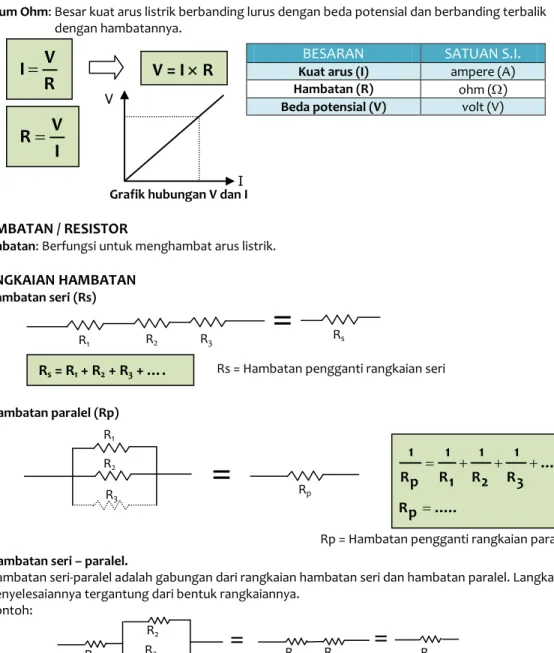
A A

HUKUM OHM DAN HAMBATAN LISTRIK

Hukum Ohm: Besar kuat arus listrik berbanding lurus dengan beda potensial dan berbanding terbalik dengan hambatannya.

HAMBATAN / RESISTOR

Hambatan: Berfungsi untuk menghambat arus listrik. RANGKAIAN HAMBATAN

1. Hambatan seri (Rs)

2. Hambatan paralel (Rp)

3. Hambatan seri – paralel.

Hambatan seri-paralel adalah gabungan dari rangkaian hambatan seri dan hambatan paralel. Langkah penyelesaiannya tergantung dari bentuk rangkaiannya.

Contoh: a.

b.

Rt = Hambatan total dari rangkaian itu. Grafik hubungan V dan I

I V

=

=

=

=

R1 R2 R3 _R1 Rp Rt

=

=

=

R1 R2 R3 Rs R3 Rt

=

=

R1 R2 R3 Rs

Rs = R1 + R2 + R3 + …. Rs = Hambatan pengganti rangkaian seri

R1 R2 R3

=

=

Rp

R

_p

...

....

3

R

1

2

R

1

1

R

1

p

R

1











Rp = Hambatan pengganti rangkaian paralel

R

V

I



V = I



R

Kuat arus (I) BESARAN SATUAN S.I. ampere (A)

Hambatan (R) ohm () Beda potensial (V) volt (V)

I

V

HUKUM I KIRCHHOFF 1. Rangkaian Seri

Dalam rangkaian seri (tidak bercabang) besar kuat arus listrik yang mengalir sepanjang rangkaian itu sama besar.

2.Rangkaian Paralel

Pada rangkaian paralel Hk.I Kirchhoff jumlah kuat arus yang masuk titik percabangan sama dengan jumlah kuat arus yang keluar dari titik percabangan itu.

Contoh :

HUKUM OHM DAN BATERAI SERI-BATERAI PARALEL 1. Baterai Tunggal 2. Baterai Seri 3. Baterai Paralel I1 = I2 = I3 = ….  Imasuk =  Ikeluar R3 R1 R2 I2 I1 I3 R

r

R

E

I





E r I

r

n

R

E

n

I









R E E r r I n = 2 R E E r r I

n

r

R

E

I





V

J

= I



R

total

I2 dan I4: kuat arus listrik yang masuk titik cabang A I1 dan I3: kuat arus listrik yang keluar dari titik cabang A Sehingga: I4 + I2 = I1 + I3



I1 _I2

I4 I3

HUKUM OHM DAN HUKUM I KIRCHHOFF DALAM SUATU RANGKAIAN LISTRIK Contoh :

Langkah-langkah penyelesaian 1. Hitung hambatan luar total (R)

2. Hitung kuat arus yang keluar dari baterai (I)

3. Hitung kuat arus listrik yang melalui masing-masing hambatan dengan mengingat hukum I Kirchhoff.

a. Bila rangkaian seri : I1 = I2 = I3 = …

b. Bila rangkaian paralel gunakan rumus sbb :

4. VAB = I  RAB VBC = I  RBC

VAC = I  RAC = VAB + VBC

5. VJepit (VJ) dapat dihitung dengan rumus:

Soal contoh diselesaikan dengan langkah-langkah di atas sbb: 1. R = 7  2. r n R E n I     A 3 8 24 I 5 , 0 2 7 12 2 I       R1 R2 R3 I1 I2 I3 VJ = I  R R1 R2 R3 A B I I1 I2 I3 3 2 1 3 2 1

R

1

:

R

1

:

R

1

I

:

I

:

I



Atau 3 AB 3 2 AB 2 1 AB 1 AB AB

R

V

I

;

R

V

I

;

R

V

I

R

I

V











Hitunglah: a. I1, I2, I3 dan I b. VAB, VBC, VAC dan VJepit R1 = 5 R2 = 3 R3 = 6 I E = 12 V r = 0,5  I1 I2 I3 E r A B C

3. Berdasarkan gambar: I1 = I = 3 A 1 : 2 6 1 : 6 2 I : I 6 1 : 3 1 I : I R 1 : R 1 I : I 3 2 3 2 3 2 3 2     Berdasarkan gambar: I1 = I2 + I3 = 3 A Maka: 3A 1 2 2 I2  _  I3 ₂1_13A I2 = 2 A I3 = 1 A INDIKATOR UN 2013 ENERGI LISTRIK

Untuk memindahkan muatan listrik (Q) dalam suatu penghantar yang kedua ujungnya memiliki beda potensial (V), diperlukan energi listrik sebesar:

Satuan SI energi listrik: joule (J) Satuan lain:

- Kwh (Kilowatt-hour):

1 Kwh = 1000 watt  3600 s = 3.600.000 J

- Kalori (kal)

1 kal = 4,2 J atau 1 J = 0,24 kal

- Kilokalori (kkal)

1 kkal = 1000 kal

W = Energi listrik I = Kuat arus listrik V = Beda potensial R = Hambatan t = waktu P = Daya listrik Q = Muatan listrik 14.Menentukan besar fisis energi atau daya listrik dalam kehidupan sehari-hari.

W = V x Q

W = I



R



I



t

W = V



I



t

t

R

2

V

W

t

R

V

V

W











W = P



t

4. VAB = I1  R1 = 3 A  5  = 15 V VBC = I2  R2 = 2 A  3  = 6 V VBC = I3 x R3 = 1 A x 6 = 6 V

DAYA LISTRIK

Daya Listrik: Besar usaha listrik yang dilakukan tiap detik.

Contoh Soal

1. Label pada sebuah lampu pijar bertuliskan seperti pada gambar. Bila lampu pijar tersebut menyala selama 8 jam, maka besar energi yang digunakan lampu tersebut adalah . . . .

A. 192 kilo joule B. 652 kilo joule C. 1.240 kilo joule D. 1.152 kilo joule Jawab : D W = P x t = 40 W x 8 x 3600 s

= 1152000 joule = 1.152 kilo joule

INDIKATOR UN 2013

CARA MEMBUAT MAGNET 1. MENGGOSOK

Besi yang akan dijadikan magnet digosok secara berulang-ulang dengan salah satu kutub magnet dengan

arah gosokan ke satu arah saja. Kutub magnet yang dihasilkan di tempat awal gosokan sama tandanya

dengan kutub magnet penggosoknya.

t

W

P



I

2

R

t

t

I

R

I

P













_{P =V}



I

R

2

V

P

R

V

R

R

V

P









P

2

V

R



Satuan SI untuk Daya Listrik : watt(W) atau joule/s Satuan lain: - kilowatt(kw) 1 kw = 1000 W

-H.P.(Horse Power) =daya kuda 1 H.P. = 746 W

15.Menjelaskan cara pembuatan magnet dan kutub-kutub yang dihasilkan.

S U Besi Magnet U S Besi S U

2. ELEKTROMAGNET

Elektromagnet: Magnet yang dibuat dari besi yang dililit kawat berarus listrik. Keuntungan elektromagnet:

1. Dapat menghasilkan kemagnetan yang kuat sekali. 2. Sifat kemagnetannya dapat hilang sama sekali.

3. Kekuatan magnetnya dapat diatur dengan mengubah besar kuat arus atau jumlah lilitan kawat. 4. Mudah penyimpanannya dan tidak perlu perawatan khusus.

Faktor-faktor yang menentukan kekuatan elektromagnet 1. Jumlah lilitan kumparan

Makin banyak lilitannya, kemagnetannya makin kuat. 2. Besar Kuat Arus listrik

Makin besar kuat arus yang mengalir dalam kumparan,kemagnetannya makin kuat. 3. Menggunakan inti besi /tidak

Inti besi lunak yang dipasang dapat memperkuat kemagnetan elektromagnet.

Untuk menentukan letak kutub magnet elektromagnet dapat menggunakan kaidah tangan kanan sbb:

 Tangan kanan dikepalkan.

 Keempat jari tangan yang dikepalkan menunjukkan arah kuat arus dalam kumparan.

 Ibu jari menunjukkan letak kutub utara magnet.

3. INDUKSI

Dengan cara mendekatkan magnet pada besi/baja.

MENGHILANGKAN SIFAT MAGNET Sifat kemagnetan dapat hilang bila: 1. Magnet dipanaskan

2. Magnet sering terjatuh/dipukul-pukul

3. Magnet disimpan di tempat yang mengandung medan magnet.

Ujung besi yang didekati oleh kutub magnet akan memperoleh kutub magnet yang berlawanan dengan kutub magnet yang didekatkan.

Magnet Besi S U S U + 

U

S

I I U

I

U