Penyelesaian masalah knapsack dengan algoritma genetika - USD Repository

(1)

i Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh: Archy Tussasy XQ

023114025

PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(2)

i Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh: Archy Tussasy XQ

023114025

PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(3)

ii THESIS

Presented As a Partial Fulfillment of The Requirements To Obtain The Sarjana Sains Degree

In Mathematics

by:

Archy Tussasy XQ 023114025

MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

(4)

(5)

(6)

v Seandainya sudah, apalagi yang harus diinginkan? Bersyukurlah apabila kita tidak tahu sesuatu. Karena itu memberimu kesempatan untuk belajar. Bersyukurlah untuk masa-masa sulit.

Dimasa itulah kita akan bertumbuh... Bersyukurlah untuk keterbatasanmu

Karena itu memnberimu kesempatan untuk berkembang Bersyukurlah untuk setiap tantangan baru

Karena itu akan membangun kekuatan dan karaktermu Bersyukurlah untuk kesalahan yang kamu buat. Karena itulah pelajaran yang berharga. Bersyukurlah Selalu!!

Karya ini kupersembahkan

Untuk Tuhan Yesus Kristus

Untuk Ayah, Ibu dan Adikku

(7)

(8)

vii

Determisnistic Polynomial Complete Problem), yang merupakan masalah yang sampai saat ini belum ditemukan adanya algoritma eksak yang dapat memberikan solusi yang eksak dalam waktu komputasi yang efisien.Pada umumnya masalah ini diselesaikan dengan algoritma pendekatan atau algoritma heuristic. Salah satu algoritma heuristic yang dapat digunakan dalam menyelesaikan masalah knapsack ini adalah Algoritma Genetika.

Sistem kerja Algoritma Genetika dimulai dari inisialisasi populasi secara random. Setiap individu di dalam populasi akan mengalami proses yang

didasarkan pada tiga operator genetik, yakni seleksi, crossover, mutasi.

(9)

viii

Deterministic Polynomial Complete Problem), that problem was not found yet about the exact algorithm that can give the exact solution in efficient computation time. Generally, this problem is solved by approached algorithm or heuristic algorithm. One of heuristic algorithm that can be used to solve knapsack problem is Genetics Algorithm.

The standard Genetic Algorithm starts with an initial population of individuals created at random. Then, this population evolves through time by a string manipulation process based in three genetic operators: reproduction,

(10)

(11)

ix

dan karuniaNya sehingga penulis dapat menyelesaikan skripsi dengan judul “Penyelesaian Masalah Knapsack dengan Algoritma Genetika”

Selama penulisan skripsi ini ada berbagai kesenangan, kesusahan, dan tantangan yang penulis hadapi. Namun karena kuasa dan campur tangan Allah sendiri yang senantiasa menaungi penulis dan keterlibatan pihak-pihak yang membantu semua hal itu dapat teratasi.

Oleh karena itu pada kesempatan yang baik ini penulis ingin mengucapkan terimakasih kepada:

1. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si. selaku Ketua Prodi Matematika, dosen pembimbing dan dosen penguji, yang telah berkenan meluangkan waktu memberikan pengarahan, motivasi, saran dan masukan dalam menyelesaikan skripsi ini.

2. Bapak Yosef Agung Cahyanta, S.T., M.T, selaku Dekan Fakultas Sains

dan Teknologi.

3. Bapak Drs. H. J Haris Sriwindono, selaku dosen pembimbing yang telah berkenan meluangkan waktu memberikan pengarahan, motivasi dan dengan penuh sabar membimbing penulis dalam menyusun skripsi ini. 4. Bapak Eko Hari Parmadi, St, S.Si., M.Kom dan Bapak Joko Nugroho, Y.,

(12)

x

6. Bapak dan Ibu Dosen Fakultas Sains dan Teknologi yang telah membantu dan membimbing penulis selama belajar di USD

7. Segenap Staff di sekretariat Fakultas Sains dan Teknologi atas bantuan dan kerjasamanya dalam melayani kepentingan mahasiswa

8. Ayahku Boyong XQ, ibuku Tuti Mulyaningsih, dan Adikku Maxi Resitama XQ atas doa, kesabaran, perhatian, kesempatan yang diberikan baik material dan spiritual sehingga skripsi ini dapat selesai.

9. Sahabat dan keluargaku di Kost “Zusi Arib”, bapak& ibu kost, N3, Mitha, Lian, Meme, Imeth, Alin, M’Tutik, M’Mely, Makdum, Evi, Kasis, Indah, Coy, Iles, Ina yang telah memberi kasih sayang, perhatian, motivasi selama menyusun skripsi dan menempuh kuliah di USD.

10. Damasus Arif Syaifudin,dan Sahabatku Agung Cole, Nusi A, Novita C yang telah membantu dalam penyusunan skripsi.

11. Ibu Yossie Retnaningrum, BA. selaku Kepala Sekolah, Ibu Lanny Kristiani ( Sie Kurikulum), rekan-rekan kerja yang lain di SMP Pantekosta dan Keluarga Besar Yayasan Sekolah Pantekosta Magelang yang telah memberikan doa ndan motivasi dalam penyusunan skripsi.

(13)

xi

masih perlu penyempurnaan dari teman sekalian. Semoga skripsi ini bermanfaat bagi kita semua.

(14)

xii

HALAMAN PENGESAHAN……….. iii

HALAMAN PERSEMBAHAN………... iv

PERNYATAAN KEASLIAN KARYA………... v

ABSTRAK……….... vi

ABSTRACT………. vii

KATA PENGANTAR………... viii

DAFTAR ISI……….... xi

DAFTAR TABEL……….... xiv

DAFTAR GAMBAR... xv

DAFTAR LAMPIRAN………... xiv

BAB I PENDAHULUAN 1 A. Latar Belakang Masalah...1

B. Perumusan Masalah………. 4

C. Pembatasan Masalah……… 4

D. Tujuan Penulisan……….. 5

E. Metode Penulisan ……… 5

F. Manfaat Penulisan……… 5

(15)

xiii

B. Algoritma Genetika………. 8

1. Pengantar Algoritma Genetika………8

2. Deskripsi Algoritma Genetika………...10

3. Struktur Umum Algoritma Genetika……….. ...13

4. Operator dan Fungsi Evaluasi………... 15

5. Pengkodean………... ...16

5.1 Pengkodean Biner………... 16

5.2 Pengkodean Permutasi……….... 17

5.3 Pengkodean Nilai……….18

5.4 Pengkodean Pohon………18

6. Seleksi……… 19

6.1 Seleksi Roda Roulette………. 19

6.2 Seleksi Ranking………... 20

6.3 Seleksi Tournament………. 21

7. Evolusi………....22

7.1 Persilangan / Crossover………... 22

7.1.1 Persilangan Satu Titik………. 23

7.1.2 Persilangan Dua titik………... 24

7.2 Mutasi……….. 24

(16)

xiv

2. Pembangkitan Kromosom……….. 35

3. Pencarian Nilai Fitness Untuk Masing-masing kromosom ………..36

4. Pemilihan Kromosom Untuk Dijadikan Orang Tua……...37

5. Proses Reproduksi Untuk Mendapatkan Kromosom Baru ...38

a. Operasi Persilangan………. ….39

b. Operasi Mutasi……….…..40

6. Skema Update Generasi………. 41

BAB IV

IMPLEMENTASI DAN ANALISA HASIL PROGRAM

43

A. Flowchart……….…43

B. Analisis Hasil Program………...44

BAB V PENUTUP 48 1. Kesimpulan……….. 48

2. Saran……… 48

DAFTAR PUSTAKA……….. 51

(17)

xv

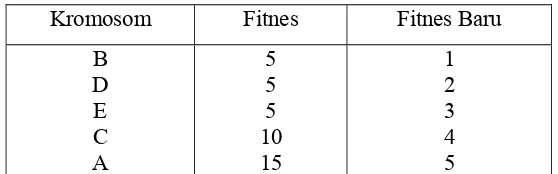
Tabel 2. 2. 6. 1 Contoh populasi dengan 5 kromosom yang diberi

fitness baru... 21

Tabel 2. 3. 1. 1 Contoh masalah knapsack……….... 28

Tabel 2. 3. 1. 2 Tabel feasible solution knapsack dengan pendekatan

matematika... 29

(18)

xvi

Gambar 2. 2. 5. 1 Contoh kromosom dengan pengkodean biner... 17

Gambar 2. 2. 5. 2 Contoh kromosom dengan pengkodean permutasi... 17

Gambar 2. 2. 5. 3 Contoh kromosom dengan pengkodean nilai... 18

Gambar 2. 2. 5. 4 Contoh kromosom dengan pengkodean pohon...19

Gambar 2. 2. 6. 1 Contoh penggunaan metode seleksi roda roulette... 20

Gambar 2. 2. 7. 1. 1 Contoh proses persilangan 1 titik ... 24

Gambar 2. 2. 7. 1. 2 Contoh proses persilangan 2 titik ... 24

Gambar 2. 2. 7. 2 Contoh proses Mutasi... 25

Gambar 3. 1. 2 Contoh inisialisasi populasi awal sebanyak 10 kromosom... 36

Gambar 3. 1. 5. 1 Contoh perkawinan silang 1 titik pada titik ke 5... 40

(19)

xvii

2. Listing program Menu... 53

3. Listing program Contoh... 53

4. Listing program Count... 54

5. Listing program Inisialisasi kromosom... 64

6. Listing program Pencarian nilai fitness………... 64

7. Listing program Menampilkan Nilai Fitness... 65

8. Listing program Menghitung Linear Fitness Ranking……… 66

9. Listing program MenampilkanFitness Ranking……….. 66

10. Listing program Proses seleksi... 67

11. Listing program Operasi Persilangan atau Crossover... 67

12. Listing program Mutasi... 68

13. Listing program tampil... 68

(20)

1 BAB I PENDAHULUAN

A. Latar Belakang Masalah.

Manusia dalam mengatasi berbagai masalah, perlu adanya suatu alat

bantu yang diyakini dapat memberikan suatu penyelesaian yang terbaik dari

permasalahan yang ada. Lalu manusia mulai berpikir untuk dapat membuat

atau menciptakan peralatan-peralatan tersebut. Salah satu teknologi yang

berhasil diciptakan manusia dalam bidang komputasi adalah mesin komputer.

Perkembangan teknologi komputer dewasa ini sangat pesat, baik dari

segi hardware maupun software. Pada dasarnya fungsi awal komputer adalah

sebagai alat bantu hitung. Karena alasan itulah mesin komputer telah dapat

berkembang luas sampai saat ini, tetapi pemakaian komputer sebagai alat

komputasi melekat pada dirinya sendiri. Salah satunya adalah dalam pencarian

solusi yang optimal pada masalah knapsack.

Masalah knapsack bila dipikirkan lebih luas, sangat banyak dijumpai

dalam kehidupan sehari-hari. Masalah knapsack termasuk dalam kelompok

masalah optimasi yang disebut masalah NP-Complete(Non Deterministic

Polynomial Complete Problem), yaitu masalah yang sangat sulit ditemukan

solusinya. Kesulitan dalam masalah knapsack berasal dari tidak mungkinnya

menghasilkan suatu algoritma yang memberikan hasil eksak dalam waktu

komputasi cepat. Masalah knapsack memerlukan banyak perhitungan serta

(21)

Dan pada umumnya masalah-masalah NP-Complete itu diselesaikan dengan

algoritma pendekatan atau algoritma heuristik.

Algoritma genetika merupakan suatu metode penyelesaian masalah

yang tergolong heuristik. Algoritma genetika dapat memberikan kemungkinan

penyelesaian masalah yang sangat banyak dan mempertimbangkan suatu

kemungkinan tersebut dalam mengambil keputusan. Algoritma genetika telah

digunakan pada masalah-masalah yang tergolong sulit dan dalam berbagai

variasi telah diterapkan ke berbagai masalah sains dan teknik yang salah

satunya adalah masalah knapsack.

Algoritma genetika pertama kali diperkenalkan oleh John Holland dan

murid-muridnya di Universitas Michigan pada tahun 1960. Algoritma

genetika adalah algoritma yang berdasarkan konsep teori evolusi alam dan

genetika. Teori evolusi alam dan genetika pertama kali dikemukakan oleh

Charles Darwin. Dalam teori genetika disebutkan bahwa sifat tertentu dari

suatu makhluk hidup ditentukan oleh susunan gen dan kromosom makhluk

hidup tersebut. Teori genetika dalam algoritma genetika digunakan untuk

mempresentasikan setiap solusi dari masalah yang ada, karena setiap solusi

diandaikan mempunyai kromosom yang berbeda dengan solusi yang lainnya.

Sedangkan evolusi alam adalah proses seleksi terhadap anggota dari berbagai

populasi berdasarkan tingkat ketahanan hidup suatu makhluk hidup.

Proses-proses dalam evolusi alam yang digunakan dalam algoritma genetika adalah

seleksi alam dan reproduksi. Proses seleksi alam digunakan untuk memilih

(22)

solusi baru yang diharapkan mempunyai kromosom lebih baik dari solusi

tersebut masing-masing memiliki nilai (profit) pi yang berbeda-beda. Yang

(23)

besar algoritma genetika akan memberikan hasil yang efisien. Dalam hal ini

diberikan juga penyelesaian secara Zero-One(0/1) karena dalam pemilihan

barang dari sejumlah barang yang ada sedemikian hingga jumlah barang

yang diambil mempunyai nilai( profit ) yang maksimal tetapi total beratnya

tidak melebihi kapasitas knapsack( kopor/ ransel ) yang ada. Dan setiap

barang yang ada tidak dapat dipecah atau dibagi lagi, atau barang tersebut

hanya mempunyai kemungkinan diambil atau ditinggalkan.

B. Perumusan Masalah

Pokok-pokok permasalahan yang akan dibahas dalam skripsi ini

adalah:

1. Bagaimana penerapan algoritma genetika pada masalah knapsck.

2. Bagaimana membuat program untuk mendapatkan himpunan

bagian dari n obyek tersebut yang dapat mengisi tepat atau kurang

dari kapasitas ransel tersebut(masalah knapsack)?

C. Pembatasan Masalah

Pembahasan skripsi ini dibatasi pada:

1. Ruang solusi hanya terdiri dari dua permasalahan yaitu mencari hasil yang

paling baik secara Zero-One pada knapsack tersebut atau menentukan

secara jelas nilai 0 atau 1 pada barang yang akan dipilih(nilai 1 berarti

barang diambil sedangkan nilai 0 berarti barang tidak diambil/

(24)

2. Barang yang akan dipilih bersifat utuh dan tidak dapat dibagi atau dipecah.

3. Algoritma pemograman yang digunakan adalah algoritma genetika.

4. Jumlah barang dibatasi maksimal 100 obyek.

D. Tujuan Penulisan

Tujuan dari penulisan skripsi ini adalah untuk menambah pengetahuan

kepada pembaca mengenai algoritma genetika dan masalah knapsack, serta

penerapan algoritma genetika untuk masalah knapsack.

E. Metode Penulisan

Penulisan skripsi ini menggunakan metode studi pustaka yaitu dengan

menggunakan buku-buku, jurnal-jurnal, dan makalah-makalah yang telah

dipublikasikan, sehingga tidak ditemukan hal baru.

F. Manfaat Penulisan

Manfaat yang diharapkan dari penulisan skripsi ini adalah dapat

menyelesaikan masalah knapsack dengan waktu yang lebih singkat dengan

algoritma genetika.

G. Sistematika Penulisan

Bab pertama adalah pendahuluan, yang berisi tentang latar belakang

masalah, perumusan masalah, pembatasan masalah, tujuan penulisan, metode

(25)

Bab kedua adalah landasan teori,pada bab ini diuraikan tentang latar

belakang biologi, algoritma genetika, pengertian masalah knapsack.

Bab ketiga adalah penerapan algoritma genetika untuk masalah

knapsack,pada bab ini akan menguraikan mengenai langkah-langkah

algoritma genetika dalam menyelesaikan masalah knapsack, representasi

masalah, pembentukan kromosom, pencarian nilai fitness masing-masing

kromosom, operasi perkawinan silang, dan operasi mutasi.

Bab keempat adalah implementasi dan analisa hasil program,pada bab

ini berisi tentang implementasi sistem yang dibangun, meliputi penjelasan

flowchart, menampilkan hasil program saat dijalankan dan analisa hasil program.

Bab kelima adalah penutup,pada bab ini berisi kesimpulan dan saran

dari sistem yang telah dibangun berdasarkan hasil pembahasan bab-bab

(26)

A. Latar Belakang Biologi

Semua mahkluk hidup terdiri dari beberapa sel.Didalam

masing-masing sel terdapat himpunan kromosom yang identik. Kromosom

merupakan untaian DNA yang membentuk model yang membedakan

masing-masing organisme. Sebuah kromosom terdiri dari gen-gen yang

merupakan blok dari suatu DNA. Dan masing-masing gen mengkodekan

sebuah susunan protein tertentu. Gen-gen tersebut mengkodekan sebuah

trait (ciri bawaan), seperti warna mata, warna kulit, dan lain-lain. Kemungkinan “settings” untuk sebuah trait(seperti warna hitam, biru,

coklat pada warna mata)disebut dengan allele. Masing-masing gen

mempunyai posisi tersendiri di dalam kromosom, posisi ini disebut locus.

Saat melakukan reproduksi, yang muncul pertama kali adalah

rekombinasi (crossover atau persilangan). Gen-gen dari induk (parents)

saling berekombinasi membentuk kromosom yang baru (offspring).

Keturunan baru (offspring) ini juga dapat bermutasi. Mutasi merupakan perubahan yang terjadi pada elemen suatu DNA. Perubahan ini terjadi

mungkin disebabkan karena kesalahan penggandaan gen-gen dari induknya

(27)

Ruang pencarian.

Ketika mencari penyelesaian suatu masalah, maka dicari solusi yang

terbaik dari semua kemungkinan solusi yang ada. Kumpulan semua

kemungkinan solusi tersebut berada dalam ruang pencarian (search space). Setiap titik pada ruang pencarian merupakan satu solusi yang mungkin

(feasible solution) dan dapat diberi pengenal dalam bentuk nilai atau

fitness-nya terhadap masalah yang akan diselesaikan. Proses pencarian solusi

menjadi rumit jika tidak diketahui di mana harus mencari atau pencarian

dimulai dari mana. Banyaknya metode yang dikenal untuk menemukan

solusi yang layak, diantaranya adalah algoritma genetika yang dibuat

berdasarkan analogi mekanisme yang terjadi terhadap proses evolusi.

B. Algoritma Genetika

1. Pengantar Algoritma Genetika

Algoritma genetika pertama kali diperkenalkan oleh John Holland

dan murid-muridnya di Universitas Michigan pada tahun 1960. Saat ini

algoritma genetika mulai banyak digunakan pada masalah-masalah yang

tergolong sulit dan dalam berbagai variasi telah diterapkan ke berbagai

masalah sains dan teknik yaitu masalah optimasi yang kompleks.

Algoritma ini merupakan metode optimasi yang tidak berdasarkan

matematika, melainkan berdasarkan pada fenomena alam yang dalam

penelusurannya mencari titik optimal berdasarkan ide yang ada pada

(28)

menyatakan bahwa evolusi jenis-jenis spesies makhluk hidup dan

ekosistemnya terjadi karena seleksi alam. Individu yang lebih kuat (fit)

akan memiliki tingkat survival dan tingkat reproduksi yang lebih tinggi

jika dibandingkan dengan individu yang kurang fit. Beberapa aplikasi

yang dapat diselesaikan dengan algoritma genetika yaitu sistem

dinamikal nonlinear, lintasan robot, program LISP, perancangan jaringan

syaraf tiruan, strategi perencanaan, Film-copy Deliverer Problem,

Knapsack Problem, Quadratic Assigment Problem, Traveling Salesman

Problem dan Minimum Spanning Tree Problem.

Algoritma genetika merupakan suatu metode penyelesaian yang

tergolong heuristik. Algoritma heuristik adalah algoritma yang mencari

penyelesaian dengan menggunakan masalah optimasi dengan

menggunakan algoritma eksak yang ada.

Ciri-ciri dari algoritma heuristik adalah:

i. Akan selalu memberikan solusi yang baik walaupun belum

tentu merupakan solusi yang optimal.

ii. Lebih cepat dan mudah untuk mengimplementasikan

daripada algoritma eksak yang diketahui menjamin

memberikan solusi yang lebih optimal.

Sedangkan ciri-ciri dari algoritma genetika adalah:

i. Bekerja dengan sebuah himpunan pengkodean solusi yang

(29)

ii. Mencari solusi dari suatu populasi yang bukan merupakan

sebuah solusi yang tunggal.

iii. Menggunakan informasi fungsi fitness.

iv. Menggunakan operasi random dengan aturan perubahan

probabilitas, bukan operasi dengan aturan tertentu dalam

setiap iterasi.

2. Deskripsi Algoritma Genetika

Algoritma genetika adalah teknik pencarian stokastik yang

berdasarkan pada mekanisme seleksi alam dan sifat genetika. Dalam

implementasinya, algoritma genetika meniru beberapa proses yang

terdapat pada evolusi alam dimana evolusi terjadi pada kromosom yang

mengkodekan struktur makhluk hidup. Individu-individu yang ada pada

saat tertentu dalam suatu populasi merupakan individu-individu yang

berhasil mempertahankan hidupnya sedangkan yang lemah akan punah.

Individu-individu yang berhasil mempertahankan hidupnya akan

membentuk individu baru.

Beberapa teori dasar evolusi yang diadopsi oleh algoritma genetika

adalah:

a. Evolusi adalah proses seleksi alam dan reproduksi yang bekerja

pada kromosom.

b. Seleksi alamiah berhubungan dengan kinerja dari struktur yang

(30)

c. Proses reproduksi adalah titik dimana terjadi evolusi.

Rekombinasi akan menciptakan kromosom baru yang berbeda

dengan induknya, demikian pula dengan mutasi.

Teori dasar evolusi tersebut bila diimplementasikan dalam bentuk

algoritma genetika, maka diharapkan mampu menyelesaikan

masalah-masalah yang sulit dengan cara yang sama seperti yang dilakukan

melalui evolusi.

Keuntungan algoritma genetika adalah sifat metode pencariannya

yang lebih optimal, tanpa terlalu memperbesar ruang pencarian dan

tanpa kehilangan kesempurnaan (completness) sehingga dapat dengan mudah diimplementasikan ke suatu permasalahan.

Algoritma genetika merupakan algoritma yang bermanfaat dan

efisien, ketika:

a. Pencarian dalam ruang pencarian yang besar, kompleks

atau hanya sedikit yang diketahui.

b. Tidak ada analisis matematika yang memungkinkan.

c. Kurang atau tidak ada pengetahuan yang memadai untuk

merepresentasikan masalah ke dalam ruang pencarian yang

lebih sempit.

d. Metode konvensional sudah tidak mampu menyelesaikan

masalah yang dihadapi.

Algoritma genetika berbeda dengan teknik optimasi konvensional

(31)

1) Algoritma genetika bekerja dengan sebuah himpunan

pengkodean dari sekumpulan solusi, bukan pada solusi itu

sendiri.

2) Algoritma genetika mencari beberapa solusi dari sebuah

populasi, bukan satu solusi.

3) Algoritma genetika menggunakan fungsi fitness, bukan menggunakan turunan atau pengetahuan lainnya.

4) Algoritma genetika menggunakan aturan perubahan

probabilistik, bukan aturan deterministik.

Istilah-istilah yang digunakan dalam algoritma genetika, dijelaskan

dalam tabel dibawah ini:

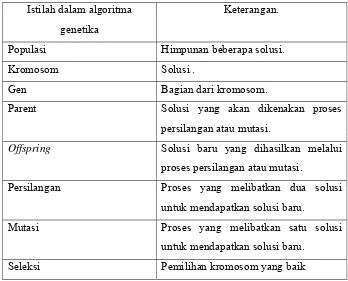
Tabel 2.2.2.1 Tabel istilah dalam Algoritma Genetika

Istilah dalam algoritma

genetika

Keterangan.

Populasi Himpunan beberapa solusi.

Kromosom Solusi .

Gen Bagian dari kromosom.

Parent Solusi yang akan dikenakan proses

persilangan atau mutasi.

Offspring Solusi baru yang dihasilkan melalui proses persilangan atau mutasi.

Persilangan Proses yang melibatkan dua solusi

untuk mendapatkan solusi baru.

Mutasi Proses yang melibatkan satu solusi

untuk mendapatkan solusi baru.

(32)

3. Struktur Umum Algoritma Genetika

Bila P(t) dan C(t) adalah induk dan keturunan pada generasi t,

struktur umum algoritma genetika adalah sebagai berikut:

prosedur algoritma genetika : begin

t ← 0;

inisialisasi P(t); evaluasi P(t);

while(kondisi terminasi tidak terpenuhi) do rekombinasi P(t) untuk menghasilkan anak C(t);

evaluasi C(t);

seleksi P(t+1) dari P(t) dan C(t);

t ← t+1;

end end

Struktur umum algoritma genetika (Mitsuo Gen dan Runwei

(33)

Ilustrasi Algoritma Genetika

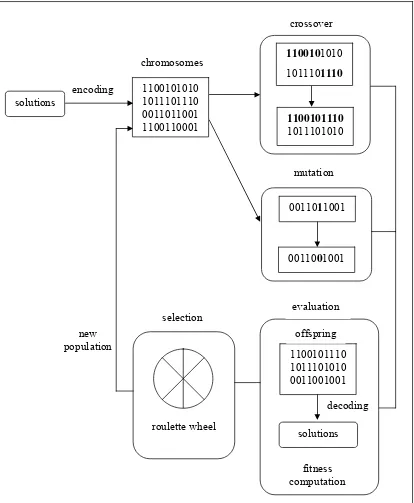
Gambar 2.2.3.1 Ilustrasi Algoritma Genetika

mutation

0011011001

0011001001 crossover

1100101010 1011101110

1100101110 1011101010

solutions evaluation

1100101110 1011101010 0011001001

offspring

fitness computation

decoding 1100101010

1011101110 0011011001 1100110001 chromosomes

selection

roulette wheel solutions

encoding

(34)

Keterangan Gambar 2.2.3.1

Dalam menyelesaikan masalah, algoritma genetika diawali dengan

menginisialisasikan himpunan solusi yang dibangkitkan secara acak. Himpunan

solusi ini disebut populasi. Setiap individu pada populasi disebut kromosom yang

menggambarkan sebuah solusi dari masalah yang akan diselesaikan. Sebuah

kromosom dapat dinyatakan dalam simbol string misalnya kumpulan string bit.

Kromosom-kromosom dapat berubah terus menerus disebut dengan regenerasi.

Pada setiap generasi, kromosom dievaluasi dengan mengunakan alat ukur yang

disebut fungsi fittnes (tingkat kesesuaian). Untuk membuat generasi berikutnya, kromosom-kromosom baru yang disebut offspring (keturunan) terbentuk dengan cara menggabung dua kromosom dari generasi sekarang dengan menggunakan

operator crossover (persilangan) atau mengubah sebuah kromosom dengan

menggunakan operator mutasi. Generasi baru dibentuk dengan cara seleksi yang

dilakukan terhadap parents dan offspring berdasarkan nilai fitness-nya dan menghilangkan yang lainnya. Kromosom-kromosom yang lebih sesuai memiliki

probabilitas untuk dipilih. Setelah beberapa generasi, algoritma ini akan

konvergen ke arah bentuk kromosom yang terbaik, dengan harapan dapat

menyatakan solusi optimal dari permasalahan yang diselesaikan.

4. Operator dan Fungsi Evaluasi

Biasanya, inisialisasi diasumsikan secara random. Rekombinasi

(35)

yaitu operasi genetik (crossover/persilangan dan mutasi dan operasi evolusi (seleksi). Pada teori evolusi, mutasi ini merupakan operator kromosom yang memungkinkan makhluk hidup melakukan penyesuaian dengan

lingkungannya walaupun lingkungan barunya tidak sesuai dengan lingkungan

induknya semula.

Faktor terbesar dalam teori evolusi yang menyebabkan suatu

kromosom bertahan, punah, melakukan persilangan atau mutasi adalah

lingkungan. Pada algoritma genetika, factor lingkungan diperankan oleh

fungsi evaluasi. Fungsi evaluasi menggunakan kromosom sebagai masukan

dan menghasilkan angka tertentu yang menunjukkan kinerja pada masalah

yang diselesaikan. Pada masalah optimasi, fungsai evaluasi adalah fungsi

tujuan (objective function). Nilai fungsi evaluasi disebut nilai kesesuaian (fitness value). Nilai inilah yang akan menentukan apakan suatu string akan muncul pada generasi berikutnya atau mati.

5. Pengkodean

Beberapa jenis pengkodean yang sering digunakan dalam

mengkodekan solusi terhadap suatu masalah, yaitu:

5.1 Pengkodean Biner (Binary Encoding)

Pengkodean biner ini merupakan cara pengkodean yang paling

umum digunakan.Karena pengkodean ini merupakan yang pertama kali

digunakan dalam algoritma genetika oleh Holland. Dalam pengkodean

(36)

Kromosom1 : 1 0 1 0 1 0 0 1

Kromosom2 : 0 0 1 1 1 0 1 0

Gambar 2.2.5.1 Contoh kromosom dengan pengkodean biner

Pengkodean biner memberikan banyak kemungkinan untuk

kromosom walaupun jumlah allele yang sedikit yaitu 0 atau 1. Pada pihak lain, pengkodean biner ini sering tidak sesuai untuk masalah dan

kadang pengoreksian harus dilakukan setelah proses evolusi (perkawinan

silang dan/atau mutasi). Contoh masalah yang sesuai untuk pengkodean

biner antara lain masalah knapsack.

5.2 Pengkodean permutasi (Permutation Encoding)

Pengkodean permutasi dapat digunakan dalam masalah

pengurutan( ordering problem). Dalam pengkodean permutasi setiap

kromosom merupakan suatu barisan bilangan yang menyatakan bilangan

dalam suatu urutan.

Kromosom1 : 1 3 4 2 6 5 7 8

Kromosom2 : 3 4 6 1 5 2 8 7

Gambar 2.2.5.2 Contoh kromosom dengan pengkodean permutasi

Pengkodean permutasi hanya berguna untuk masalah pengurutan.

Contoh yang menggunakan pengkodean permutasi adalah masalah

(37)

5.3 Pengkodean nilai (Value Encoding)

Pengkodean nilai dapat digunakan untuk masalah yang mempunyai

nilai yang rumit. Dengan pengkodean nilai, setiap kromosom merupakan

suatu barisan dari nilai-nilai. Nilai-nilai dapat berupa apa saja yang

berhubungan dengan masalah, bilangan biasa, bilangan riil, karakter

sampai ke obyek-obyek yang rumit.

Kromosom1 : 1.2 5.3 0.4 2.3 2.4 4.1 3.5 1.9

Kromosom2 : A B D J E I F J

Gambar 2.2.5.3 Contoh kromosom dengan pengkodean nilai

Pengkodean nilai ini baik digunakan untuk beberapa masalah. Di

pihak lain, untuk mengkodekan tipe ini sering perlu pengembangan

persilangan dan mutasi baru yang spesifik untuk permasalahannya.

Contohnya dalam masalah mencari bobot untuk jaringan syaraf.

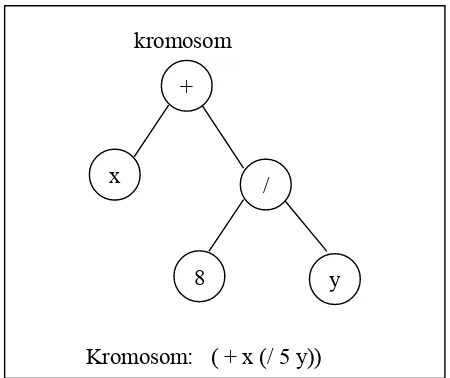
5.4 Pengkodean pohon (Tree Encoding)

Pengkodean pohon ini lebih banyak digunakan untuk menyusun

program atau ekspresi bagi pemrograman genetika. Dalam pengkodean

pohon, setiap kromosom merupakan suatu pohon dari beberapa objek,

seperti fungsi atau perintah dalam bahasa pemrograman.

Pengkodean pohon ini baik digunakan untuk menyusun

program.Contoh masalah yang menggunakan pengkodean pohon adalah

(38)

kromosom

Gambar 2.2.5.4 Contoh kromosom dengan pengkodean pohon

6. Seleksi

Seleksi akan menentukan individu-individu mana saja yang akan

dipilih untuk dilakukan rekombinasi dan bagaimana offspring/keturunan terbentuk dari individu-individu terpilih. Langkah pertama yang dilakukan

dalam seleksi ini adalah pencarian nilai fitness. Ada beberapa metode seleksi,

antara lain:

6.1 Seleksi Roda Roulette

Metode seleksi roda roulette merupakan metode yang paling

sederhana, dan sering juga dikenal dengan nama stochastic sampling with replacement. Sesuai dengan namanya, metode ini menirukan permainan roulette-wheel di mana masing-masing kromosom menempati

potongan lingkaran pada roda roulette secara proporsional sesuai dengan +

x _/

y 8

(39)

nilai fitnessnya. Kromosom yang mempunyai nilai fitness lebih besar

menempati potongan lingkaran yang lebih besar dibandingkan dengan

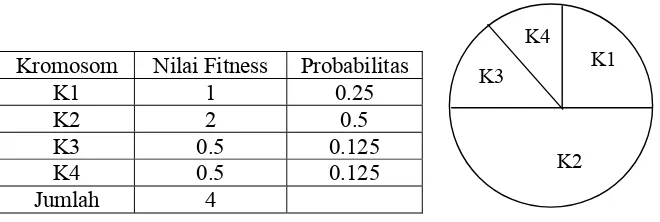
kromosom bernilai fitness rendah. Gambar 2.2.6.1 ilustrasi sebuah contoh penggunaan metode roda roulette.

Kromosom Nilai Fitness Probabilitas

K1 1 0.25 K2 2 0.5

K3 0.5 0.125

K4 0.5 0.125

Jumlah 4

Gambar 2.2.6.1Contoh penggunaan metode seleksi roda roulette.

Kromosom K1 mempunyai probabilitas 25% untuk dipih setiap

kali suatu kromosom dipilih (setiap roda diputar). Probabilitas

masing-masing individu dapat dicari dari pembagian fitness masing-masing-masing-masing

individu dengan total fitness dalam populasi.

Seleksi dengan roda roulette berdasarkan skala fitness. Karena

terpilihnya suatu kromosom dalam populasi untuk dapat berkembang

biak adalah sebanding dengan fitnesnya, maka akan terjadi

kecenderungan kromosom yang baik akan terpelihara terus sehingga

dapat membawa ke hasil optimum lokal (konvergensi dini) ke suatu hasil

yang bukan optimim global. Sebaliknya, jika semua kromosom dalam

populasi mempunyai fitness yang hamper sama, maka seleksi ini akan

menjadi seleksi yang bersifat acak.

K3 K4

K1

(40)

(41)

secara acak dengan probabilitas yang sama. Dari k kromosom yang

terpilih tersebut kemudian dipilih suatu kromosom dengan fitness

terbaik, yang diperoleh dari hasil pengurutanrangking fitness

kromosom-kromosom yang dipilih tersebut.

Perbedaan dengan seleksi roda Roulette adalah bahwa pemilihan

kromosom yang akan digunakan untuk berkembang biak tidak

berdasarkan skala fitness dari populasi. Untuk k = 1, seleksi turnamen ini

akan sama dengan seleksi secara acak karena hanya melibatkan satu

kromosom. Untuk k = 2, maka dua kromosom dalam populasi akan

dipilih secara acak, kemudian dari dua kromosom tersebut dipilih satu

kromosom dengan fitness tersebut. Biasanya yang sering digunakan

adalah untuk k = 2 tergantung dari ukuran populasi.

7. Evolusi

7.1 Persilangan / Crossover

Salah satu komponen paling penting dalam algoritma genetika

adalah persilangan atau crossover. Persilangan atau crossover berfungsi menggabungkan dua string induk yang berbeda menjadi dua string

keturunan yang berbeda dengan induknya. Sebuah kromosom yang

mengarah pada solusi yang bagus dapat diperoleh dari proses

persilangan dua buah kromosom. Persilangan bisa juga berakibat buruk

jika ukuran populasinya sangat kecil. Dalam suatu populasi yang sangat

(42)

sangat cepat menyebar ke kromosom-kromosom lainnya. Untuk

mengatasi masalah ini untuk mengatasi masalah ini dilakukan dengan

suatu probabilitas tertentu Pc. Artinya, penyilangan bisa dilakukan hanya jika suatu bilangan random [0,1) yang dibangkitkan kurang dari Pc yang ditentukan.

Dari hasil penelitian yang sudah pernah dilakukan oleh praktisi

algoritma genetika menunjukkan bahwa angka probabilitas persilangan

sebaiknya cukup tinggi, yaitu 80% sampai 95% untuk memberikan hasil

yang baik. Untuk beberapa masalah tertentu probabilitas persilangan

60% memberikan hasil yang lebih baik (Obitko,1998). Segera setelah

induk untuk persilangan terpilih maka digunakan operasi persilangan

sehingga terbentuk keturunan dari induk tersebut.

Ada beberapa persilangan / Crossover:

7.1.1. Persilangan satu titik

Proses persilangan ini adalah dengan memilih satu

titik persilangan. Kromosom offspring kemudian dibentuk

sebagai barisan bit dari awal kromosom sampai titik

persilangan. Yang disalin dari induk pertama selebihnya

disalin dari induk ke dua.

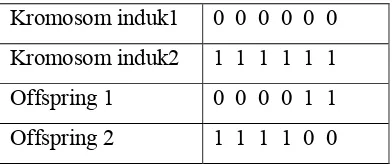
Sebagai contoh, andaikan terdapat dua kromosom

induk dengan panjang L = 6 yaitu 000000 dan 111111. Jika

titik persilangan adalah 4 maka dihasilkan dua offspring

(43)

Kromosom induk1 0 0 0 0 0 0

Kromosom induk2 1 1 1 1 1 1

Offspring 1 0 0 0 0 1 1

Offspring 2 1 1 1 1 0 0

Gambar 2.2.7.1.1 Contoh proses persilangan satu titik

7.1.2. Persilangan dua titik

Proses persilangan ini adalah memilih dua titik

persilangan. Kromosom offspring kemudian dibentuk

sebagai barisan bit dari awal sampai titik persilangan

pertama disalin dari induk pertama, bagian dari titik

persilangan pertama dan kedua disalin dari induk kedua,

kemudian selebihnya disalin dari induk pertama lagi.

Sebagai contoh, andaikan terdapat dua kromosom

induk dengan panjang L = 6 yaitu 000000 dan 111111. Jika

terdapat dua titik persilangan yaitu 2 dan 4 maka dihasilkan

2 offspring yaitu 001100 dan 110011.

Kromosom 1 0 0 0 0 0 0

Kromosom 2 1 1 1 1 1 1

Offspring 1 0 0 1 1 0 0

Offspring 2 1 1 0 0 1 1

Gambar 2.2.7.1.2 Contoh proses persilangan dua titik

7.2 Mutasi

Setelah proses persilangan selesai, kemudian dilakukan proses

(44)

mengubah nilai dari satu atau beberapa gen dalam 1 kromosom. Mutasi

berfungsi dalam melakukan peruban yang bukan disebabkan oleh

persilangan.

Jika dalam proses pemilihan kromosom-kromosom cenderung

terus pada kromosom yang baik saja maka sangat mudah terjadi

konvergensi dini, yaitu mencapai solusi optimum lokal. Untuk

menghindari terjadinya konvergensi dini dan tetap menjaga perbedaan

kromosom-kromosom dalam populasi, selain melakukan penekanan

selektif yang lebih efisien, operasi mutasi juga dapat dilakukan.

Proses mutasi ini adalah acak, sehingga tidak selalu menjamin

bahwa setelah proses mutasi akan diperoleh kromosom fitnes yang lebih

baik, tetapi dengan adanya mutasi ini diharapkan agar kromosom yang

diperoleh akan mempunyai fitnes yang lebih baik dibandingkan sebelum

operasi mutasi.

Kromosom sebelum mutasi

Kromosom sesudah mutasi

1 1 0 0 1 1 1 1 0 1 0 0

Gambar 2.2.7.2 Contoh proses mutasi

Akan tetapi operasi mutasi mendapat kontaversi penerapannya

dalam algoritma genetika karena sifatnya yang acak sehingga dapat

menggangu kromosom dengan fitnes terbaik yang telah diperoleh.

Kadang operasi mutasi tetap digunakan dengan probabilitas yang sangat

kecil yaitu Pm<1. jadi kemungkinan kromosom mengalami perubahan

(45)

C. Masalah Knapsack

Kasus yang akan dipecahkan disini dimisalkan terdapat n obyek dengan masing-masing obyeknya dikatakan sebagai((x_i;i=1,2,3,....n) yang

masing-masing obyek tersebut mempunyai berat atau disebut w_i. Setiap

obyek tersebut masing-masing memiliki nilai (profit) p_i yang berbeda-beda.

Yang menjadi permasalahan adalah bagaimana obyek-obyek tersebut dapat

dimuat atau dimasukkan kedalam ransel (Knapsack) yang mempunyai

kpasitas maksimum sebesar W sehingga timbul permasalahan sebagai

berikut:

• Bagaimana menentukan atau memilih beberapa obyek yang akan

dimuat dari n obyek yang ada sedemikian sehingga nilai kumulatif obyek yang termuat dalam ransel itu jumlahnya maksimum sesuai

dengan kapasitas ransel

(

≤W

)

?

• Jika semua obyek yang harus dimuat kedalam ransel, maka berapa

bagian dari setiap obyek yang ada dapat dimuat ke dalam ransel

sedemikian sehingga nilai kumulatifnya maksimum dan sesuai

dengan kapasitas ransel?

Penyelesaian secara Matematika

Dalam beberapa literatur, istilah lain dari fungsi tujuan dapat disebut

sebagai fungsi utama atau juga fungsi obyektif yaitu fungsi yang menjadi

penyelesaian permasalahan dengan mendapatkan solusi yang optimal. Solusi

(46)

BAB III

ALGORITMA GENETIKA

UNTUK MASALAH KNAPSACK

Pada skripsi ini akan dibuat sistem dengan menggunakan algoritma

untuk membantu user dalam menyelesaikan masalah knapsack dengan waktu yang

lebih singkat Penulis membangun sistem ini dengan menggunakan bahasa

pemrograman MATLAB.

Di bawah ini akan dituliskan secara rinci penggunaan algoritma genetika

untuk menyelesaikan masalah knapsack.

A. Analisis

A. Representasi Masalah

Hal yang paling penting dalam menyelesaikan masalah optimasi

adalah representasi atau pemodelan masalah ke dalam suatu model yang

sesuai dengan algoritma yang digunakan. Untuk menyelesaikan masalah

knapsack dengan algoritma genetika, maka masalah harus

direpresentasikan atau dimodelkan terlebih dahulu. Jenis representasi yang

dapat digunakan untuk menyelesaikan masalah Knapsack:

a. Binary representation approach

b. Order representation approach

c. Variable-length representation approach

Untuk menyelesaikan masalah knapsack akan digunakan Binary

(47)

knapsack dalam bentuk string biner 0/1. Dimana 1 berarti pemasukan salah

satu obyek dan 0 berarti pengeluaran salah satu obyek dari n obyek yang ada didalam knapsack.

Masalah knapsack dapat diformulasikan sebagai berikut: Misalkan

dipunyai sejumlah nilai p1,p2,...,pn dan jumlah S dan harus dihitung nilai

n x x

x1, 2,...., sehingga nantinya didapat hasil S = p1x1+ p2x2 +....+ pnxn.

Nilai dari koefisien xi sama dengan 1 atau 0 yag mengindikasikan bahwa

obyek ada atau tidak ada dalam ransel.

Representasi ini mengkodekan komposisi barang yang dapat

termuat dalam ransel sebagai urutan operasi dan setiap gen mewakili satu

operasi. Contoh: Misalkan terdapat 10 buah barang yang akan dimuat ke

dalam ransel (knapsack) yang mempunyai kapasitas daya muat maksimum

100 kg. Masing-masing barang tersebut mempunyi berat 40 kg, 50 kg, 30

kg, 10 kg, 10 kg, 40 kg, 30 kg, 20 kg.30 kg, dan 20 kg dan selain itu

masing-masing barang juga memiliki nilai, yaitu 40, 60, 10, 10, 3, 20, 60,

20,10, dan 20.

Tabel 3.1.1 Daftar 10 barang yang akan dimuat ke dalam ransel

n=10, W=100

Bobot/berat(w) 40 50 30 10 10 40 30 20 30 20 Nilai/profit(p) 40 60 10 10 3 20 60 20 10 20

Sasaran dari contoh ini jelas yaitu memaksimalkan nilai tanpa

(48)

pengaruh dari ukuran populasi terhadap kecepatan terjadinya konvergensi

solusi. Contoh: Salah satu solusi yang dapat mewakili masalah 10 obyek

dapat direpresentasikan dalam string bit seperti berikut:[1 1 0 1 0 0 0 0 0

0] .Ini berarti bahwa 1, 2,dan 4 terpilih untuk dimasukkan ke dalam

ransel. Penjelasan ini dapat dikategorikan sebagai sebuah solusi yang tidak

mungkin (infeasible solution).Dengan kata lain, susunan banyaknya bit-bit

yang ditentukan mungkin akan melebihi kapasitas ransel. Berikut dua

metode yang telah diusulkan untuk menangani ketidakmungkinannya :

• Penalty metoda,(metode hukuman)

• Decoder metoda (metode ahli sandi)

Metoda hukuman menugaskan satu hukuman sampai

masing-masing solusi yang tidak mungkin. Metoda ahli sandi menghasilkan solusi

dari sebuah kromosom menggunakan perkiraan-perkiraan greedy secara

heuristik.

B. Pembangkitan Kromosom

Setelah dilakukan representasi atau pemodelan masalah, kemudian

dilakukan pembangkitan kromosom. Pembangkitan kromosom dalam

masalah knapsack akan dilakukan secara acak atau random. Semakin

banyak barang dan bobot yang akan dicari total maksimal kapasitas

knapsack maka semakin banyak pula kromosom yang dibangkitkan.

Untuk inisialisasi populasi yang pertama, dalam program akan

(49)

atau 1 dengan banyaknya variable adalah 10, banyaknya bilangan yang

dirandom antara 10 sampai 100 dan probabilitasnya 0.5. Contoh

inisialisasi populasi awal dapat lihat pada Gambar 3.1.2

Kromosom ke- Bentuk representasinya

k1 1 1 0 1 0 0 0 0 0 0

k2 1 1 0 0 1 0 0 0 0 0

k3 1 0 1 1 0 0 0 1 0 0

k4 1 0 1 0 1 0 0 1 0 0

k5 1 0 1 0 0 0 1 0 0 0

k6 1 0 0 1 1 1 0 0 0 0

k7 1 0 0 1 0 0 1 1 0 0

k8 1 0 0 0 1 0 1 1 0 0

k9 1 0 0 0 0 1 0 1 0 0

k10 0 1 1 1 1 0 0 0 0 0

Gambar 3.1.2 Contoh inisialisasi populasi awal sebanyak 10 kromosom

C. Pencarian nilai fitness untuk masing-masing kromosom

Kromosom yang telah dibangkitkan akan ditentukan berdasarkan

nilai fitness-nya. Nilai fitness disini merupakan solusi dari permasalahan knapsack yaitu nilai (profit) yang maksimal untuk sejumlah obyek yang

akan dimuat dalam ransel sedemikian sehingga jumlah ransel sesuai

dengan kapasitas.Setiap kromosom yang telah dikodekan akan

diterjemahkan untuk dicari nilai fitness-nya.

Untuk menentukan fitness terbaik adalah memilih dari seluruh

(50)

(51)

setiap kromosom memiliki kemungkinan untuk terpilih menjadi parent

secara lebih merata.

D. Pemilihan kromosom untuk dijadikan orang tua

Pemilihan kromosom untuk dijadikan orang tua dilakukan

berdasarkan nilai fitnes dari masing-masing kromosom. Orang tua dipilih melalui proses seleksi. Seleksi yang digunakan adalah seleksi roda roulette

(roulette wheel selection) karena seleksi ini lebih cepat mencapai konvergensi solusi dibandingkan seleksi ranking, atau seleksi turnamen.

Cara kerja seleksi roda roulette wheel adalah menyeleksi populasi baru

dengan distribusi probabilitas yang berdasarkan nilai fitness. Semua

kromosom yang telah dicari nilai fitnes-nya ditempatkan dalam suatu

lingkaran, luas masing-masing kromosom ditentukan dari nilai fitnes-nya, semakin besar nilai fitnes dari suatu kromosom maka semakin luas tempat dari kromosom tersebut dalam lingkaran sehingga kromosom yang

mempunyai nilai fitnes yang besar mempunyai kemungkinan besar untuk

terpilih. Kemudian roda roulette akan diputar dan roda roulette akan

menunjuk kromosom yang dipilih. Anggota-anggota populasi yang terpilih

ini akan dijadikan orang tua yang nantinya akan dikenakan operasi

persilangan (crossover) dan operasi mutasi untuk mendapatkan kromosom yang lebih baik daripada sebelumnya.

Skema seleksi Roda Roulette dilakukan dengan tahapan berikut:

1. Hitung fitness untuk setiap individu, sebagai fi

(52)

3. Hitung proporsi fitness setiap individu terhadap jumlahnya,

f i i _s

f p =

4. Hitung kumulatif proporsi fitness secara berturut, menjadi

i

pc =

∑

pk, k=0,...,n

5. Buat nbilangan random pri dari 0 sampai 1 dengan

1

+ ≤

≤ i i

i pr pc

pc yang akan dijadikan induk dalam crossover.

Metode seleksi Roda Roulette dikombinasikan dengan elitism.Elitism

berguna untuk mempertahankan nilai fitness terbaik suatu generasi agar

tidak turun di generasi berikutnya. Dalam Algoritma Genetika caranya

adalah dengan mengcopykan individu terbaik(Fitness Max) sebanyak yang

dibutuhkan.

E. Proses reproduksi untuk mendapatkan kromosom-kromosom baru Untuk mendapatkan total maksimal kapasitas knapsack, diperlukan

modifikasi terhadap kromosom-kromosom. Modifikasi yang dilakukan

adalah operasi persilangan dan operasi mutasi. Operasi persilangan adalah

proses penggabungan dua kromosom (dua orang tua yang terpilih) untuk

menghasilkan dua individu baru sedangkan operasi mutasi merupakan

proses pengubahan sebuah kromosom yang terpilih untuk menghasilkan

individu baru.

a. Operasi persilangan

Setelah proses seleksi selesai dilakukan dan didapat

(53)

perkawinan silang. Perkawinan silang yang akan digunakan dalam

program, yaitu perkawinan silang 1-titik(1- point crossover)

Sebelum dilakukan perkawinan silang, acak bilangan antara 0

dan 1 dengan distribusi seragam untuk menandai setiap individu ke-I

apakah akan dilakukan perkawinan silang atau tidak. Berdasar pada

probabilitas crossover, Pc, jika individu I mempunyai Pi<Pc maka akan dilakukan perkawinan silang, dan jika sebaliknya tidak. Dalam

program akan digunakan 4 nilai Pc, yaitu

0 .

8 ;

0 .

85 ;

0 .

9 ;

0 .

95

.

Banyaknya variasi Pcdimaksudkan sebagai bahan perbandingan

analisis.

Perkawinan silang 1-titik

Dalam perkawinan silang 1-titik, 1 titik dipilih secara acak

sebagai titik perkawinan silang. Gen-gen dari kedua orang tua

kemudian diberikan ke keturunannya. Perkawinan silang 1-titik akan

menghasilkan 2 offspring. Contoh perkawinan silang 1-titik dapat dilihat pada Gambar 3.1.5.1

Gambar 3.1.5.1 Contoh perkawinan silang 1 titik pada titik ke-5.

induk anak

1 1 1 1 1 1 1 1 1 1

0 0 0 0 0 0 0 0 0 0

1 1 1 1 1 0 0 0 0 0

(54)

b. Operasi mutasi

Mutasi dilakukan untuk menghindari terjadinya konvergensi

dini.Jenis mutasi yang dilakukan adalah dengan cara mengubah bit 1

menjadi 0 atau sebaliknya 0 menjadi 1.Karena untuk semua gen yang ada,

jika bilangan random yang dibangkitkan kurang dari probabilitas mutasi

m

p yang ditentukan maka nilai gen tersebut diubah menjadi nilai

kebalikannya. Biasanyapm diset sebagai 1 , dimana _n n adalah jumlah

gen dalam kromosom. Dengan pm sebesar ini berarti mutasi hanya terjadi

pada sekitar satu gen saja. Berdasarkan mutasi tersebut maka dalam

implementasi program akan digunakan mutasi inversi 2 titik. Contoh

mutasi inversi tersebut dapat dilihat pada gambar 3.4. Mutasi inversi 2 titik

berarti ada dua gen yang mengalami inversi nilai. Langkah-langkah mutasi

adalah sebagai berikut:

1. Buat bilangan random antara 0 dan 1 sebanyak ukuran populasi

yang diinginkan dengan distribusi uniform untuk menandai

setiap individu, pi.

2. Bandingkan pi dan pm. Jika pi < pm maka akan dilakukan

mutasi sedangkan jika sebaliknya maka tidak.

3. Buat 2 kolom bilangan random dengan banyaknya baris sama

dengan ukuran populasi dengan distribusi uniform untuk

(55)

4. Untuk setiap gen yang terpilih, ubah bit 0 menjadi 1 dan bit 1

menjadi 0( mutasi inverse)

Gambar 3.1.5.2 Contoh mutasi invers

F. Skema Update generasi

Untuk mendapatkan generasi baru, maka akan dilakukan update

generasi dengan cara mengulangi proses mulai langkah mengevalusi nilai

fitness. Dalam implementasi program hanya akan digunakan satu skema

update generasi yaitu, yaitu steady-state reproduction . Prinsip kerja skema tersebut adalah hanya mengganti satu individu dalam setiap

generasi. Individu harus dihapus untuk menjaga ukuran populasi tetap

sesuai dengan jumlah individu dalam populasi. Terdapat beberapa

prosedur penghapusan individu, yaitu penghapusan individu yang bernilai

fitness paling rendah atau penghapusan individu yang paling tua.

Penghapusan bisa berlaku hanya pada individu orang tua saja atau bisa

juga berlaku pada semua individu dalam populasi.

.

induk anak

(56)

(57)

B. Analisis Hasil Program

Program aplikasi yang dibuat berfungsi untuk mencari nilai (profit) yang maksimal untuk sejumlah obyek yang akan dimuat dlam ransel

sedemikian sehingga jumlah ransel sesuai kapasitas.

Di dalam program ini parameter yang diinputkan adalah:

1. Parameter Knapsack. Parameter Knapsack diantaranya banyaknya

jumlah barang, berat, profit dan berat kapasitas maksimal ransel.

2. Parameter algoritma genetika. Parameter algoritma genetika diantaranya:

a. UkPop, merupakan banyaknya populasi yang akan dibangkitkan dan

bentuk populasi awal secara acak.

b.JumGen, merupakan banyaknya generasi yang akan dihasilkan. Jumlah

generasi besar berarti semakin banyak iterasi yang dilakukan, dan

semakin besar pula domain solusi yang akan dieksplorasi.

c. Psilang adalah probabilitas persilangan / crossover. Probabilitas ini menentukan peluang dari kromosom untuk melakukan persilangan /

crossover.

d.Pmutasi adalah probabilitas mutasi. Probabilitas mutasi ini

menentukan peluang dari gen pada setiap kromosom untuk melakukan

mutasi.

Berikut adalah pengolahan fitness dan setting parameter yang penulis

(58)

(59)

100 20

30 20 30 40 10 10 30 50

40x₁+ x₂ + x₃+ x₄ + x₅+ x₆ + x₇ + x₈+ x₉ + x₁₀ ≤

Pada program ini, fitness dihitung dengan menjumlahkan profit tiap barang yang masuk kedalam knapsack. Jika berat total dalam satu

kromosom lebih besar daripada kapasitas maksimum knapsack, maka nilai

fitnessnya diganti 0. Untuk mencegah adanya individu yang dominan dalam suatu populasi( dalam pemilihan orang tua untuk di perkawinan silang),

maka diperlukan suatu fungsi Linier Fitness Ranking

Pemilihan kromosom untuk dijadikan orang tua dilakukan

berdasarkan nilai fitness dari masing-masing kromosom. Orang tua dipilih melalui proses seleksi roda roulette yang dikombinasikan dengan elitism

agar nilai fitness terbaik suatu generasi tidak turun di generasi berikutnya. Perbandingan Hasil Perkawinan silang:

1. Pc=0,8

x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 |x10| berat | profit | ket |