1
METODE
STEEPEST DESCENT
DENGAN UKURAN
LANGKAH BARU UNTUK PENGOPTIMUMAN
NIRKENDALA
DJIHAD WUNGGULI
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
BOGOR 2015
3
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*
Dengan ini saya menyatakan bahwa tesis berjudul Metode Steepest Descent dengan Ukuran Langkah Baru utuk Pengoptimuman Nirkendala adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Februari 2015 Djihad Wungguli NIM G551120031
RINGKASAN
DJIHAD WUNGGULI. Metode Steepest Descent dengan Ukuran Langkah Baru untuk Pengoptimuman Nirkendala. Dibimbing oleh BIB PARUHUM SILALAHI dan SUGI GURITMAN.
Masalah pengoptimuman dapat dikategorikan dalam dua bagian yaitu pengoptimuman berkendala dan pengoptimuman nirkendala. Untuk menyelesaikan permasalahan pengoptimuman nirkendala, khususnya untuk fungsi nonlinear dapat digunakan metode steepest descent. Metode steepest descent merupakan prosedur paling mendasar yang diperkenalkan oleh Cauchy pada tahun 1847. Metode ini adalah metode gradien sederhana yang menggunakan vektor gradien untuk menentukan arah pencarian pada setiap iterasi. Kemudian, dari arah tersebut akan ditentukan besar ukuran langkahnya. Pada beberapa kasus, metode steepest descent ini memiliki kekonvergenan yang lambat menuju solusi optimum karena langkahnya berbentuk zig-zag. Hal ini menunjukkan bahwa masalah pemilihan ukuran langkah menjadi masalah penting. Penelitian tentang pencarian ukuran langkah diantaranya adalah metode Barzilai-Borwein, Alternatif Minimisasi dan metode Yuan.
Penelitian ini memiliki tiga tujuan utama yaitu: (1) merekonstruksi algoritme steepest descent, Barzilai-Borwein, Alternatif Minimisasi, dan algoritme Yuan; (2) memodifikasi metode steepest descent dengan ukuran langkah baru; dan (3) membandingkan secara eksperimental output dari modifikasi algoritme dengan metode steepest descent, Barzilai-Borwein, Alternatif Minimisasi, dan Yuan untuk kasus fungsi kuadratik ditinjau dari proses iterasi dan running time. Metode dalam penelitian ini disusun melalui tiga tahap, (1) melakukan telaah pustaka metode steepest descent klasik, metode Barzilai-Borwein, metode Alternatif Minimisasi dan metode Yuan, (2) memodifikasi ukuran langkah pada metode steepest descent dengan ukuran langkah yang baru, (3) mengimplementasikan algoritme tersebut menggunakan perangkat lunak. Kemudian dilakukan pengujian dan perbandingan untuk kasus fungsi kuadratik yang dibangkitkan secara acak.
Dalam penelitian ini dihasilkan dua modifikasi ukuran langkah baru disebut Algoritme (4.5) dan Algoritme (4.6). Kedua modifikasi ini merupakan gabungan dari metode steepest descent dan metode Yuan. Dari rata-rata hasil perbandingan masalah fungsi kuadratik untuk semua dimensi metode steepest descent memberikan kinerja yang buruk dibandingkan dengan metode lainnya. Selanjutnya pada masalah dengan dimensi yang kecil, metode Yuan mampu menemukan solusi nilai minimum dengan iterasi dan running time yang terkecil. Meskipun demikian Algoritme (4.5) dan (4.6) mampu menyeimbangi kecepatan metode Yuan dan mampu mengungguli hasil dari metode Barzilai-Borwein, serta metode Alternatif Minimisasi. Untuk kasus fungsi kuadratik dengan dimensi yang besar, metode Yuan memberikan hasil yang buruk. Sedangkan, Algoritme (4.5) dan (4.6) menghasilkan iterasi dan running time yang terkecil, hal ini disebabkan oleh tingkat konvergensi yang lebih cepat pada kedua metode ini.
Kata kunci: fungsi kuadratik, metode gradien, running time, steepest descent, ukuran langkah baru.
5
SUMMARY
DJIHAD WUNGGULI. Steepest Descent Method with New Step Size for Unconstrained Optimization. Supervised by BIB PARUHUM SILALAHI and SUGI GURITMAN.
The problem of optimization could be categorized into constrained and unconstrained optimization. The unconstrained optimization problem especially nonlinear function can be solved by steepest descent method. This is a basic procedure as introduced by Cauchy in 1847. It is a simple gradient method that uses gradient vector to determine the search direction in its iteration. Furthermore, from the direction will be determined the size of the step. In many cases, the steepest descent method has a slow convergence towards the optimum solution because of a zigzag steps. It involved indicates that the selection of step size problem is an important issue. There are many studies conducted on searching the step size in the steepest descent method, such as in Barzilai-Borwein, Alternative Minimization and Yuan method.
This research has three main objectives: (1) reconstructing the method of steepest descent, Barzilai-Borwein, Alternative Minimization, and the Yuan algorithms; (2) modifying the method of steepest descent by using new step sizes; and (3) comparing experimentally results of modification algorithms steepest descent, Barzilai-Borwein, Alternative Minimization, and Yuan method for quadratic function in terms of the iteration and running time process. This research composed in three stages method, (1) reviewing literatures on the classic steepest descent, Barzilai-Borwein, Alternative Minimization, and Yuan method, (2) modifying the step size in the steepest descent method by new step sizes, (3) computer implementation using software. Furthermore, testing and compared results was carried out using the quadratic function cases that generated randomly.
This research has two new step size modifications known as Algorithm (4.5) and (4.6). Both of them are combination of steepest descent and Yuan method. The average results of comparison quadratic function for all steepest descent method dimensions give poor performance compared to the other methods. While for the problem of small dimensions, the Yuan method reached the minimum value solutions with the iteration number and the running time minimum. Nevertheless, the Algorithm (4.5) and (4.6) able to compete the speed of Yuan method and perform better than the Barzilai-Borwein and Alternative Minimization method. For the quadratic functions case with large dimensions, Yuan method gives bad results. While Algorithm (4.5) and (4.6) produce the smallest of iteration and running time than the other methods, it is happen because this is related with the convergence speed within the Algorithm (4.5) and Algorithm (4.6).
Keywords: quadratic function, gradient method, running time, steepest descent, .new step size.
©
Hak Cipta Milik IPB, Tahun 2015
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis ini dalam bentuk apa pun tanpa izin IPB
7
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains
pada
Program Studi Matematika Terapan
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
BOGOR 2015
METODE
STEEPEST DESCENT
DENGAN UKURAN
LANGKAH BARU UNTUK PENGOPTIMUMAN
NIRKENDALA
9
Judul Tesis : Metode Steepest Descent dengan Ukuran Langkah Baru untuk Pengoptimuman Nirkendala
Nama : Djihad Wungguli NIM : G551120031
Disetujui oleh Komisi Pembimbing
Dr Ir Bib Paruhum Silalahi, MKom Ketua
Dr Sugi Guritman Anggota
Diketahui oleh
Ketua Program Studi Matematika Terapan
Dr Jaharuddin, MS
Dekan Sekolah Pascasarjana
Dr Ir Dahrul Syah, MScAgr
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah Subhanahu wa ta’ala atas segala nikmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Februari 2014 ini ialah teori optimasi, dengan judul Metode Steepest Descent dengan Ukuran Langkah Baru untuk Pengoptimuman Nirkendala. Penulisan tesis ini merupakan salah satu syarat memperoleh gelar Magister Sains pada program studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor.
Dalam proses penulisan tesis ini, penulis menyadari bahwa telah memperoleh dorongan dan bantuan baik moril maupun materil dari berbagai pihak untuk melengkapi keterbatasan-keterbatasan yang dimiliki penulis. Untuk itu, melalui kesempatan ini penulis ingin mengucapkan terima kasih dan rasa hormat yang sebesar-besarnya kepada:
1. Bapak Dr Ir Bib Paruhum Silalahi, MKom selaku pembimbing I dan Bapak Dr Sugi Guritman selaku pembimbing II.
2. Dr Jaharuddin, MS selaku Ketua Program Studi Matematika Terapan. 3. Seluruh dosen dan staf pegawai tata usaha Departemen Matematika.
4. Direktorat Jenderal Pendidikan Tinggi (DIKTI) sebagai sponsor Beasiswa Unggulan.
5. Ayahanda dan Ibunda tercinta, Bapak Usman Wungguli dan Ibu Hadidjah Luther, Adik Rahmad Wungguli dan Rini Wahyuni Mohamad serta seluruh keluarga yang selalu memberikan dorongan dan mendoakan untuk keberhasilan studi bagi penulis.
6. Seluruh mahasiswa Departemen Matematika khususnya teman-teman angkatan tahun 2012 di program studi S2 Matematika Terapan.
7. Seluruh rekan–rekan mahasiswa Asrama Gorontalo di Bogor.
8. Sahabat-sahabat yang tak dapat disebutkan satu persatu yang telah banyak membantu penulis dalam penyelesaian tesis ini.
Semoga segala bantuan, bimbingan, dan motivasi yang telah diberikan kepada penulis senantiasa mendapat balasan dari Allah Subhanahu wa ta’ala.
Akhirnya, semoga penulisan tesis ini dapat memperkaya pengalaman belajar serta wawasan kita semua.
Bogor, Februari 2015 Djihad Wungguli
11
DAFTAR ISI
DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi 1 PENDAHULUAN 1 Latar Belakang 1 Tujuan Penelitian 2 2 TINJAUAN PUSTAKA 3 Ruang Vektor 3 Matriks 4 Ortogonalitas 5 Pengoptimuman Matematik 6 Turunan Parsial 6 Turunan Berarah 6Vektor Gradien dan Matriks Hesse 7
Minimum Global dan Minimum Lokal 8
Fungsi Kuadratik di 8 Kedefinitan Matriks 8 Kekonveksan Fungsi 9 Tingkat Konvergensi 9 Deret Taylor 10 Ketaksamaan Kantorovich 10
Iterasi dan Running Time 10
3 METODE PENELITIAN 11
4 HASIL DAN PEMBAHASAN 11
Metode Steepest Descent 11
Exact Line Search 14
Kekonvergenan Metode Steepest Descent 17
Metode Barzilai dan Borwein 19
Metode Alternatif Minimisasi 20
Metode Yuan 22
Modifikasi Metode Steepest Descent dengan Ukuran Langkah Baru 25
Hasil Numerik 26
5 SIMPULAN 31
DAFTAR PUSTAKA 31
LAMPIRAN 32
DAFTAR TABEL
1 Rata-rata jumlah iterasi dari metode steepest descent 27 2 Rata-rata running time dari metode steepest descent 28
DAFTAR GAMBAR
1 Pencarian arah d gradien terhadap vektor gradien 12
2 Ilustrasi steepest descent dalam plot kontur 13
3 Ilustrasi perbandingan metode Alternatif Minimisasi dan metode
steepest descent 21
4 Perbandingan rata-rata iterasi dan running time dari metode steepest
descent untuk λn = 10 29
5 Perbandingan rata-rata iterasi dan running time dari metode steepest
descent untuk λn = 100 29
6 Perbandingan rata-rata iterasi dan running time dari metode steepest
descent untuk λn = 1000 29
7 Kekonvergenan dari metode steepest descent 30
DAFTAR LAMPIRAN
1 Sintaks dari setiap metode steepest descent 32
1 PENDAHULUAN
Latar Belakang
Dalam aktivitas sehari-hari sering dijumpai kegiatan yang menyangkut pengoptimuman. Kegiatan pengoptimuman ini bertujuan untuk memaksimumkan atau meminimumkan. Hal ini biasanya dijumpai dalam bidang industri, teknik, ekonomi, pertanian dan banyak sektor bidang lainnya. Pengoptimuman dapat didefinisikan sebagai proses untuk mendapatkan keputusan terbaik yang memberikan nilai maksimum atau minimum dari suatu fungsi dengan cara penentuan solusi yang tepat. Dari segi fungsinya pengoptimuman dapat dibedakan menjadi pengoptimuman linear dan pengoptimuman nonlinear. Sedangkan dari bentuknya pengoptimuman dikelompokkan menjadi pengoptimuman berkendala dan pengoptimuman nirkendala. Pengoptimuman berkendala adalah pengoptimuman suatu fungsi dengan syarat-syarat tertentu yang membatasinya. Sebaliknya pengoptimuman nirkendala adalah pengoptimuman tanpa adanya syarat-syarat tertentu yang membatasinya (Griva et al. 2009).
Kegiatan Pengoptimuman selalu identik dengan nilai maksimum atau nilai minimum yang terbaik. Padahal, pengoptimuman yang baik seharusnya mempertimbangkan juga metode yang akan digunakan serta pemrograman yang tepat dalam aspek komputasi. Komputasi dapat diartikan sebagai cara untuk menemukan pemecahan masalah dari data input dengan menggunakan suatu algoritme dalam menyelesaikan suatu masalah. Dalam aspek komputasi hal yang diperhatikan adalah kompleksitas ruang dan kompleksitas waktu. Hal ini dapat dilihat dari tingkat kerumitan serta waktu yang dibutuhkan dari suatu algoritme dalam menyelesaikan suatu fungsi. Suatu algoritme dikatakan baik jika tingkat kerumitannya semakin kecil dan prosesnya membutuhkan waktu yang kecil. Namun pada kenyataannya banyak metode pengoptimuman yang bentuknya sederhana akan tetapi membutuhkan waktu yang lama dalam proses komputasinya. Oleh karenanya sangat diperlukan suatu perbaikan dari motode pengoptimuman baik dari segi kompleksitas ruang maupun dari segi kompleksitas waktunya.
Metode pengoptimuman umumnya dapat dilakukan secara analitik maupun secara numerik. Namun untuk kasus pengoptimuman nirkendala dengan fungsi nonlinear multivariabel, terdapat persoalan yang tidak bisa diselesaikan dengan metode analitik. Sehingga diperlukan metode numerik untuk menyelesaikan permasalahan tersebut. Metode numerik yang digunakan dalam masalah pengoptimuman biasanya bersifat iteratif. Salah satu metode iteratif yang digunakan adalah metode line search steepest descent.
Metode steepest descent (SD) merupakan prosedur paling mendasar untuk meminimumkan fungsi terdiferensialkan beberapa variabel yang diperkenalkan oleh Cauchy pada tahun 1847 (Bazaraa et al. 2006). Metode ini adalah metode gradien sederhana yang menggunakan vektor gradien ( ) (turunan parsial orde pertama dari fungsi f ) untuk menentukan arah pencarian disetiap iterasi dan dari arah tersebut akan ditentukan besar ukuran langkahnya ( ). Pada beberapa kasus, metode SD ini memeliki kekonvergenan yang lambat ketika menuju ke solusi optimum, hal ini terjadi karena langkahnya yang berbentuk zig-zag. Secara
intuitif arah yang digunakan dalam metode SD adalah arah dengan penurunan yang tercepat, akan tetapi secara umum tidak berarti menuju titik minimum lokal yang tercepat. Sehingga dalam beberapa tahun terakhir ini menjadi lebih jelas bahwa pimilihan ukuran langkah menjadi masalah penting dalam metode steepest descent. Penentuan ukuran langkah ini dapat mempengaruhi cepat atau lambatnya kekonvergenan ke solusi optimum. Sebuah hasil yang mengejutkan diberikan oleh Barzilai dan Borwein (1988) yang berusaha menyempurnakan metode ini dengan memodifikasi algoritme dan hasilnya berjalan cukup baik untuk masalah dengan dimensi yang besar. Metode ini kemudian dikenal dengan metode Barzilai-Borwein (BB)
Hasil metode BB (1988) telah memicu banyak penelitian pada metode steepest descent. Penelitian-penelitian yang dilakukan untuk mendapatkan algoritme pencarian ukuran langkah yang memungkinkan konvergensi cepat dan monoton. Diantaranya penelitian yang dilakukan oleh Dai dan Yuan (2003) yang dinamakan Alternatif Minimisasi (AM) dengan ide penggabungan ukuran langkah yang bergantian antara meminimumkan nilai fungsi dan norm gradien disepanjang garis steepest descent. Penelitian lainnya dilakukan oleh Yuan (2006), dengan algoritme ukuran langkah baru pada iterasi genap dan exact line search pada iterasi ganjil. Metode Yuan ini sangat efisien untuk masalah dengan dimensi kecil. Berdasarkan penelitian-penelitian yang telah dilakukan, maka dalam penelitian ini akan dimodifikasi ukuran langkah pada metode SD dengan ukuran langkah baru untuk memperoleh kekonvergenan yang lebih cepat dari metode-metode yang telah dilakukan sebelumnya. Modifikasi ukuran langkah yang dilakukan diharapkan dapat memperkecil kompleksitas ruang maupun kompleksitas waktu yang dibutuhkan dari algoritme.
Tujuan Penelitian
a. Merekonstruksi algoritme steepest descent, Barzilai-Borwein, Alternatif Minimisasi, dan metode Yuan.
b. Memodifikasi algoritme steepest descent dengan ukuran langkah baru.
c. Membandingkan secara eksperimental hasil output dari modifikasi algoritme dengan metode steepest descent, Barzilai-Borwein, Alternatif Minimisasi, dan metode Yuan untuk kasus fungsi kuadratik ditinjau dari proses iterasi dan running time.
3
2 TINJAUAN PUSTAKA
Ruang Vektor Definisi 2.1 (Ruang Vektor)
Misalkan V adalah himpunan dengan pendefinisian operasi penjumlahan dan operasi perkalian dengan skalar. Setiap pasangan elemen dan di dalam V terdapat suatu elemen yang tunggal juga berada di dalam V serta setiap elemen di dalam V dan setiap skalar terdapat yang tunggal juga berada di dalam V. Himpunan V dengan operasi penjumlahan dan operasi perkalian dengan skalar ini dinamakan ruang vektor jika memenuhi aksioma berikut.
1. .
2. ( ) ( ) .
3. sehingga . 4. terdapat ( ) sehingga ( ) . 5. ( ) dan skalar .
6. ( ) dengan skalar dan skalar . 7. ( ) dengan skalar dan skalar .
8. .
Elemen dalam V adalah vektor sedangkan symbol 0 menyatakan vektor nol. (Leon 1998) Definisi 2.2 (Ruang Bagian)
Jika S adalah himpunan bagian takkosong dari suatu ruang vektor V dan S memenuhi syarat-syarat berikut
1. jika untuk sembarang skalar
2. jika dan , maka S disebut ruang bagian dari V.
(Leon 1998) Definisi 2.3 (Kombinasi Linear)
Misalkan adalah vektor-vektor dalam suatu ruang vektor V. Jumlah vektor-vektor yang berbentuk dengan skalar-skalar disebut kombinasi linear dari .
(Leon 1998) Definisi 2.4 (Merentang)
Misalkan adalah vektor-vektor dalam suatu ruang vektor V. Himpunan vektor dikatakan merentang suatu vektor V jika setiap vektor pada V selalu dapat dinyatakan sebagai kombinasi linear dari vektor
.
(Leon 1998) Definisi 2.5 (Bebas Linear)
Vektor-vektor dalam ruang vektor V disebut bebas linear
jika mengakibatkan semua skalar-skalar
harus sama dengan nol.
Definisi 2.6 (Bergantung Linear)
Vektor-vektor dalam ruang vektor V disebut bergantung linear jika terdapat skalar-skalar yang tidak semuanya nol sehingga .
(Leon 1998) Definisi 2.7 (Basis)
Vektor-vektor membentuk basis untuk ruang vektor V jika dan hanya jika bebas linear dan merentang V .
(Leon 1998) Definisi 2.8 (Dimensi)
Misalkan V adalah ruang vektor. Jika V memiliki basis yang terdiri atas n vektor, maka V dikatakan memiliki dimensi n .
(Leon 1998)
Matriks Definisi 2.9 (Matriks Identitas)
Matriks identitas adalah matriks ( ) yang berukuran , dengan {
(Leon 1998) Definisi 2.10 (Invers dari Suatu Matriks)
Suatu matriks yang berukuran dikatakan taksingular jika terdapat matriks B sehingga . Matriks B dikatakan invers multiplikatif dari matriks . Invers multiplikatif dari matriks taksingular secara sederhana disebut juga sebagai invers dari matriks dan dinotasikan dengan .
(Leon 1998) Definisi 2.11 (Traspose dari Suatu Matriks)
Transpos dari suatu matriks ( ) yang berukuran adalah matriks ( ) yang berukuran yang didefinisikan oleh untuk setiap dan . Transpos dari dinotasikan oleh .
(Leon 1998) Definisi 2.12 (Matriks Simetris)
Suatu matriks berukuran disebut matriks simetris jika
(Leon 1998) Definisi 2.13 (Matriks Diagonal)
Matriks diagonal adalah matriks berukuran yang semua unsur selain diagonal utama ialah nol. Matriks diagonal berukuran dapat ditulis sebagai
[ ]
dengan disebut unsur diagonal utama. Matriks diagonal D memiliki invers yang dapat dinyatakan sebagai
5 n d d d D 1 0 0 0 1 0 0 0 1 2 1 1
Dengan semua unsur diagonal utama adalah taknol sehingga . Matriks dapat dikatakan matriks simetris karena .
(Anton & Rorres 2005)
Ortogonalitas Definisi 2.14 (Hasil Kali Skalar)
Misalkan dengan , - dan ,
-maka hasil kali skalar dari adalah
( )
(Leon 1998) Definisi 2.15 (Norm)
Suatu pemetaan ‖ ‖ disebut norm jika dan hanya jika memenuhi sifat berikut:
(i) ‖ ‖ ‖ ‖
(ii) ‖ ‖ | |‖ ‖ (iii)‖ ‖ ‖ ‖ ‖ ‖
Untuk , maka dari didefinisikan sebagai:
‖ ‖ (∑| |
)
⁄
( )
Dalam prakteknya, hanya tiga yang digunakan yaitu:
‖ ‖ ∑| | ‖ ‖ (∑| | ) ⁄ ‖ ‖ | | Norm vektor lainnya yang sering digunakan adalah norm ellipsoid yang didefinisikan sebagai
‖ ‖ ( ) ⁄ ( )
Misalkan dengan , - , maka norm dari vektor di adalah
‖ ‖ √ √ ( )
(Sun dan Yuan 2006) Definisi 2.16 (Ortogonal)
Vektor – vektor dan disebut ortogonal jika .
Pengoptimuman Matematik Definisi 2.17
Pengoptimuman matematik adalah suatu proses formulasi masalah dan penentuan solusi dari suatu masalah pengoptimuman berkendala dengan bentuk umum: ( ) , - dengan kendala (2.16) ( ) ( )
dimana ( ) ( ) ( ) adalah fungsi dari x.
Komponen-komponen dari , - dinamakan variabel keputusan, ( ) adalah fungsi objektif, ( ) menyatakan fungsi kendala pertaksamaan, ( ) adalah fungsi-fungsi kendala persamaan. Vektor optimum yang menjadi solusi dari masalah dinyatakan dengan dan nilai optimumnya adalah ( ). Jika tidak ada kendala maka masalah dinamakan masalah pengoptimuman nirkendala.
(Snyman 2005) Turunan Parsial
Definisi 2.18
Andaikan bahwa f adalah suatu fungsi dua variabel x dan y. Jika y di jaga agar tetap konstan, katakanlah , maka ( ) adalah fungsi satu variabel x. Turunannya di x = x0 disebut turunan parsial f terhadap x di ( ) dan
dinyatakan oleh ( ). Jadi
( )
( ) ( )
( )
Dengan cara serupa, turunan parsial f terhadap y di ( ) dinyatakan oleh
( ) dan diberikan oleh
( )
( ) ( )
( )
Misalkan f suatu fungsi tiga variabel x, y, dan z. Turunan parsial f terhadap x di (x,y,z) dinyatakan oleh ( ) dan didefenisikan oleh
( )
( ) ( )
( )
Turunan parsial terhadap y dan z didefenisikan secara serupa.
(Varberg et al. 2007) Turunan Berarah
Definisi 2.19
Untuk tiap vektor u, misalkan
( )
( ) ( )
( )
7 Untuk menghitung turunan berarah dari suatu fungsi, biasanya digunakan teorema berikut:
Teorema 2.1
Misalkan f terdiferensialkan di p, maka f mempunyai turunan berarah di p dalam arah vektor satuan u = (a, b) dan
( ) ( ) ( )
yaitu
( ) ( ) ( ) ( ) (Varberg et al. 2007)
Vektor Gradien dan Matriks Hesse Definisi 2.20 (Vektor Gradien)
Untuk fungsi ( ) yang terdapat di setiap titik yang merupakan vektor dari turunan parsial orde pertama disebut vektor gradien yaitu:
( ) ( ( ) ( ) ( )) ( ) ( )
Definisi 2.21 (Matriks Hesse)
Jika fungsi f terdiferensialkan secara kontinu dua kali maka di titik terdapat matriks turunan parsial kedua yang disebut matriks Hesse:
( ) , ( ) - ( ) ( ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ) ( )
dimana ( ) adalah matriks simetrik .
Minimum Global dan Minimum Lokal Definisi 2.22
Titik adalah minimum global dari f pada D jika ( ) ( )
Titik adalah minimum lokal jika terdapat sehingga
( ) ( ) * |‖ ‖ +
dengan ‖ ‖ menyatakan norm Euclid.
Syarat perlu dan syarat cukup untuk minimum lokal dinyatakan dalam teorema berikut:
Teorema 2.2 (Syarat perlu)
Misalkan adalah fungsi yang mempunyai turunan parsial kedua di . Jika adalah minimum lokal, maka ( ) , (syarat orde pertama) dan matriks Hesse ( ) semidefinit positif (syarat orde kedua).
Titik sehingga ( ) dinamakan titik kritis atau titik stasioner fungsi f.
Teorema 2.3 (Syarat cukup)
Misalkan adalah fungsi yang mempunyai turunan parsial kedua di . Jika ( ) dan matriks Hesse ( ) definit positif, maka adalah minimum lokal dari .
(Snyman 2005)
Fungsi Kuadratik di Definisi 2.23
Suatu fungsi dinamakan fungsi kuadratik dalam n variabel jika dapat dituliskan sebagai
( ) ( )
Dengan , b vektor real berukuran n, dan A matriks real berukuran . Jika maka
( ) (2.26)
( )
Sehingga matriks adalah matriks simetrik.
(Snyman 2005)
Kedefinitan Matriks Teorema 2.4
Misalkan matriks berukuran dan misalkan adalah minor utama ke-k dari matriks untuk maka
1. definit positif jika dan hanya jika , untuk k = 1,2,…,n,
9 Teorema 2.5
Jika suatu matriks simetrik, maka matriks adalah
1. definit positif jika dan hanya jika semua nilai eigen dari adalah positif, 2. definit negatif jika dan hanya jika semua nilai eigen dari adalah negatif, 3. takdefinit jika dan hanya jika mempunyai paling sedikit satu nilai eigen
positif dan paling sedikit satu nilai eigen negatif.
(Peressini et al. 1988)
Kekonveksan Fungsi Definisi 2.24 (Ruas Garis)
Misalkan dan dua titik di , maka ruas garis yang menghubungkan dan adalah
* | ( ) + (2.27)
Definisi 2.25 (Himpunan Konveks)
Himpunan dikatakan himpunan konveks jika dan hanya jika untuk setiap dan di C, maka ruas garis yang menghubungkan dan juga terletak di C.
Definisi 2.26 (Fungsi Konveks) Misalkan ,
1. fungsi f dikatakan konveks pada himpunan konveks C jika
( ( ) ) ( ) ( ) ( ) ( )
untuk setiap , di C dan untuk setiap dengan
2. fungsi f dikatakan konveks sempurna pada himpunan konveks C jika
( ( ) ) ( ) ( ) ( ) ( )
untuk setiap , di C dengan dan untuk setiap dengan
Misalkan ( ) mempunyai turunan parsial kedua yang kontinu pada suatu himpunan C di . Jika matriks Hesse ( ) dari f adalah definit positif pada C, maka ( ) adalah fungsi konveks sempurna pada C.
(Snyman 2005)
Tingkat Konvergensi Defenisi 2.27
Misalkan diberikan barisan iterasi * + yang dihasilkan oleh suatu algoritme konvergen ke pada sejumlah norm yaitu,
‖ ‖ ( ) Jika terdapat bilangan real dan bilangan konstan positif yang bebas terhadap iterasi k, sehingga
‖ ‖
maka dapat dikatakan * + memiliki -order tingkat konvergensi yang dapat dibagi menjadi tiga bagian:
1. jika dan ( ) maka barisan * + konvergen Q-Linear
2. jika dan atau, dan maka barisan * +
konvergen Q-Superlinear
3. jika maka barisan * + konvergen Q-Kuadrat
(Sun dan Yuan 2006)
Deret Taylor Definisi 2.28
Deret Taylor dari fungsi real ( ) yang terturunkan untuk semua tingkatan disekitar titik dapat ditulis sebagai berikut:
( ) ( ) ( ) ( )
( ) ( )( ) ( )
dimana ( ) adalah gradien pada dan ( ) adalah matriks Hessian. (Varberg et al. 2007)
Ketaksamaan Kantorovich Teorema 2.6
Diberikan matriks simetrik definit positif dengan nilai eigen
. Maka untuk setiap berlaku Ketaksamaan:
( )
(( ))(( ))
( ) ( )
(Sun dan Yuan 2006)
Iterasi dan Running Time Definisi 2.29 (Iterasi)
Iterasi adalah sifat tertentu dari algoritme atau program komputer dimana suatu urutan atau lebih dari langkah algoritmik yang dilakukan pada loop program. Iterasi merupakan proses yang dilakukan secara berulang dalam menyelesaikan permasalahan matematik.
(Chapman 2008) Definisi 2.30 (Running Time)
Running time dari suatu algoritme didefenisikan sebagai ukuran operasi primitif atau tahapan proses yang dieksekusi.
3 METODE PENELITIAN
Penelitian ini disusun melalui tiga tahap, pertama dilakukan telaah pustaka (buku dan jurnal terkait) mengenai metode steepest descent. Pada tahap pertama ini akan merekonstruksi empat metode gradien steepest descent yaitu metode steepest descent klasik, metode Barzilai-Borwein, metode Alternatif Minimisasi dan metode Yuan. Selanjutnya pada tahap kedua, memodifikasi ukuran langkah pada metode steepest descent dengan ukuran langkah yang baru. Kemudian pada tahap ketiga, mengimplementasikan metode kedalam bahasa pemrograman dengan menggunakan perangkat lunak. Setelah itu, dilakukan pengujian untuk kasus fungsi kuadratik yang dibangkitkan secara acak. Rata-rata dari hasil pengujian akan dibandingkan untuk melihat metode yang terbaik dalam menemukan solusi nilai minimum dengan iterasi dan running time yang terkecil.
4 HASIL DAN PEMBAHASAN
Metode Steepest Descent
Seperti yang telah dijelaskan dalam pendahuluan bahwa metode steepest descent adalah metode gradien sederhana untuk pengoptimuman nirkendala. Metode ini digunakan untuk meminimumkan fungsi terdiferensialkan beberapa variabel yang menggunakan vektor gradien ( ) (turunan parsial orde pertama dari fungsi f ) untuk menentukan arah pencarian disetiap iterasi. Metode ini diperkenalkan pertama kali oleh Cauchy pada tahun 1847 dengan bentuk permasalah pengoptimuman:
( ) ( ) dimana ( ) adalah fungsi terdiferensialkan secara kontinu di . Secara umum
( ) dapat berupa fungsi nonlinear.
Metode steepest descent merupakan metode iteratif untuk memperoleh solusi pendekatan dari problem awal. Dalam pembahasan metode iteratif ini, vektor yang diperoleh pada iterasi ke-k dinyatakan dengan . Misalkan diberikan suatu titik awal kemudian akan dicari , sehingga ( ) ( ). Pergerakan pada setiap iterasi haruslah memenuhi
( ) ( ) (4.2) Misalkan f adalah fungsi yang terdefinisi di yang mempunyai turunan parsial pertama yang kontinu. Arah descent ditentukan dengan menggunakan turunan berarah di . Misalkan ( ) ( ) dan . Dengan menggunakan aturan rantai diperoleh
( ) ( ) (4.3)
sehingga
menyatakan laju perubahan ( ) di pada arah , yang disebut juga dengan turunan berarah dari ( ) di pada arah (Gambar 1).
Gambar 1 Pencarian arah d gradien terhadap vektor gradien Perhatikan bahwa
( ) ‖ ( )‖‖ ‖ ‖ ( )‖ (4.5) dimana adalah sudut antara ( ) dengan . Karena maka
‖ ( )‖ ‖ ( )‖ ‖ ( )‖ (4.6)
Di titik dicari vektor satuan sehingga turunan berarah mempunyai nilai terkecil relatif terhadap semua kemungkinan vektor satuan di . Nilai terkecil dari turunan berarah tersebut adalah ‖ ( )‖ pada saat , yaitu pada saat sudut antara ( ) dengan adalah , yang berarti sudut antara
( ) dengan adalah 0. Jadi vektor arah berimpit dengan vektor
( ). Ini berarti arah sehingga turunan berarah fungsi di sekecil mungkin adalah ( ).
Secara umum metode steepest descent memiliki bentuk sebagai berikut:
( ) (4.7)
atau
(4.8)
dimana dan ( ) adalah vektor gradien dari ( ) di dan > 0 adalah ukuran langkah. Ukuran langkah dapat diperoleh dengan pencarian exact line search yaitu:
* ( )+ (4.9)
Jika ingin menemukan nilai minimum dari ( ) ( ) maka dapat dilakukan dengan mencari ( ) sehingga diperoleh
( ) ( ) ( ) (4.10) ini berarti gradien dari titik saat ini dan gradien dari titik selanjutnya saling tegak lurus (ortogonal). Untuk batas keturunan nilai fungsi untuk setiap iterasi dalam exact line search diberikan oleh,
〈 ( )〉 ( )
‖ ‖‖ ( )‖ ( )
dimana 〈 ( )〉 menunjukkan sudut antara dan ( ). Lebih jelasnya teori kekonvergenan exact line search dijelaskan pada subbab selanjutnya.
dk
13 Metode steepest descent selalu konvergen. Artinya, secara teori metode ini tidak akan berhenti atau akan terus melakukan iterasi sampai titik stasionernya ditemukan. Adapun algoritme stespest descent dituliskan dalam tahap-tahap sebagai berikut:
Algoritme 4.1 Steepest Descent
Step 0. Diberikan titik awal dan batas toleransi . Tetapkan .
Step 1. Tentukan . Jika ‖ ‖ , berhenti. Jika tidak tentukan
.
Step 2. Tentukan yang meminimumkan
( )
( )
Step 3. Hitung
Step 4. Beri nilai , dan pergi ke Step 1.
Pada algoritme metode steepest descent ini memerlukan sembarang nilai awal atau titik awal . Pemberian nilai awal ini merupakan kriteria dari suatu metode iteratif. Selanjutntya dalam metode ini membutuhkan batas toleransi ( ) yang digunakan untuk pemberhentian dari proses iteratif. Batas toleransi ini digunakan untuk membatasi nilai ‖ ‖. Pembatasan ini dilakukan untuk menentukan tingkat ketelitian dari solusi. Semakin kecil batas toleransi yang diberikan maka solusi dari permasalahan akan semakin mendekati ke nilai yang sebenarnya. Pada dasarnya dalam metode steepest descent terdapat beberapa kriteria untuk pembatasan proses iterasi atau disebut uji konvergensi diantaranya yaitu norm dari selisih dua nilai terakhir yang disimbolkan dengan ‖
‖. Selain itu dapat juga menggunakan selisih dari dua nilai fungsi terakhir yaitu
| ( ) ( )|. Untuk kriteria pembatasan proses iterasi ini dapat digunakan secara bersamaan sehingga proses iterasi akan berhenti ketika salah satu kreteria terpenuhi.
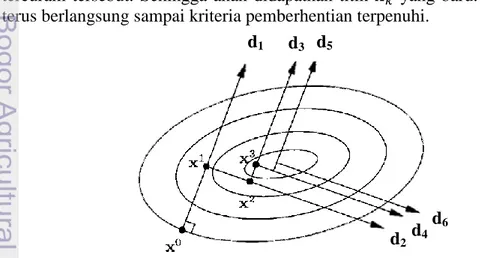
Selanjutnya langkah terpenting dalam metode steepest descent yaitu menentukan vektor gradien dan menentukan ukuran langkah . Vektor gradien digunakan untuk menentukan arah dimana suatu kurva ( ) pada titik mengalami penurunan yang tercuram sedangkan ukuran langkah digunakan untuk menentukan seberapa besar ukuran atau langkah pada arah penurunan tercuram tersebut. Sehingga akan didapatkan titik yang baru. Proses ini akan terus berlangsung sampai kriteria pemberhentian terpenuhi.
Gambar 2 Ilustrasi steepest descent dalam plot kontur (Snyman 2005). d1 d3 d5
d2d4
Meskipun titik optimum lokal ditemukan dengan arah yang tercuram metode steepest descent sering berkinerja buruk mengikuti jalan zig-zag. Hal ini menyebabkan konvergensi lambat dan menjadi ekstrim ketika masalah dengan skala yang besar yaitu ketika bentuk kontur yang sangat panjang. Kinerja yang buruk ini disebabkan oleh fakta bahwa metode steepest descent memberlakukan secara berturut arah pencarian yang ortogonal (4.10) seperti yang ditunjukkan pada Gambar 2. Meskipun dari sudut pandang teoritis metode ini dapat terbukti menjadi konvergen, tetapi dalam prakteknya metode ini tidak dapat secara efektif konvergen dalam jumlah langkah terbatas. Hal ini tergantung pada titik awal yang diberikan, bahkan konvergensi buruk ini juga terjadi ketika menerapkan metode steepest descent walaupun untuk fungsi kuadratik yang definit positif.
Exact Line Search
Line search adalah pencarian satu dimensi yang mengacu pada prosedur pengoptimuman untuk fungsi dengan variabel tunggal. Line search ini merupakan dasar dari pengoptimuman multivariabel (4.8) untuk mencari Nilai dapat dicari dengan meminimumkan fungsi tujuan pada arah dan dapat dituliskan sebagai berikut: ( ) ( ) atau (4.12) ( ) ( )
Line search biasanya dinamakan exact line search karena berdasarkan (4.12) dapat ditemukan titik minimum yang tepat dan titik stasioner dari fungsi. Untuk lebih jelasnya akan dibuktikan kekonvergenan dari exact line search.
Teorema 4.1 (Teori Kekonvergenan untuk Exact Line Search)
Misal diberikan yang merupakan solusi dari (4.12). Dimisalkan pula
‖ ( ) ‖ , dimana M adalah bilangan positif, maka
( ) ( )
‖ ( )‖ 〈 ( )〉 ( )
Bukti.
Dari ekspansi deret Taylor diperoleh:
( ) ( ) ( ) ‖ ‖ ( ) ( )
dari asumsi ‖ ( ) ‖ , sehingga
( ) ( ) ( ) ‖ ‖ ( )
dimisalkan ̅ ( )⁄( ‖ ‖ ) sehingga dari (4.15) dan (4.11) diperoleh
( ) ( ) ( ) ( ̅ )
̅ ( ) ̅ ‖ ‖
( ( ))
15
‖ ( )‖
( ( ))
‖ ‖ ‖ ( )‖
‖ ( )‖ 〈 ( )〉
Teorema 4.2 (Teori Kekonvergenan untuk Exact Line Search)
Misalkan ( ) adalah fungsi kontinu terdiferensialkan pada himpunan terbuka , diasumsikan barisan dari (4.12) memenuhi ( ) ( )
dan ( ) . Misalkan ̅ merupakan titik akumulasi dari * + dan merupakan indeks dengan * | ̅+. Diasumsikan juga terdapat
sehingga ‖ ‖ . Jika ̅ adalah titik akumulasi dari * +
maka
( ̅) ̅ (4.16) Selanjutnya, jika ( ) terdiferensialkan dua kali pada maka
̅ ( ̅) ̅ (4.17)
Bukti
Misalkan merupakan indeks dengan ̅ . Jika ̅
maka (4.16) memiliki solusi trivial. Jika tidak maka dipertimbangkan dua kasus berikut.
(i)Terdapat indeks sehingga ̅ . Karena merupakan ukuran langkah yang tepat, maka ( ) . Karena ‖ ‖ merupakan terbatas seragam dan , maka diambil hasil limit
( ̅) ̅
(ii) Untuk ̅ . Misalkan adalah indeks dari dengan ̅ ⁄ . Andaikan bahwa (4.16) tidak benar maka
( ̅) ̅
Jadi terdapat lingkungan ( ̅) dari ̅ dan indeks sehingga ( ̅) dan ,
( ) ⁄
Misal ̂ adalah bilangan positif terkecil, sehingga untuk ̂ dan
, ( ̅). Pilih ( ̅ ⁄ ̂), maka dari exact line search dan ekspansi Taylor diperoleh
( ̅) ( ) ∑, ( ) ( ∑ , ( ) ( ∑ , ( ) (
∑ ( )
∑ ( )
dimana . Kontradiksi di atas menunjukkan bahwa (4.16) juga berlaku untuk kasus (ii).
Untuk pembuktian (4.17) sama halnya dengan pembuktian (4.16) yaitu secara kontradiksi hanya berbeda pada ekspansi deret Taylor orde kedua dan memisalkan ̅ ( ̅) ̅ ⁄ . ( ̅) ( ) ∑, ( ) ( ∑ , ( ) ( ∑ * ( ) ( ) ( ) ( ) + ∑ ( ) ( ) ∑ [ ( )] ( )
Hal ini kontradiksi dengan (4.17).
Dalam kasus pengoptimuman dengan fungsi kuadratik (2.25) pencarian dengan exact line search dapat diubah dalam bentuk sederhana. Misalnya secara umum akan diminimumkan ( ) ( ) dengan arah descent . Karena masalah pengoptimuman berbentuk fungsi kuadratik (2.25) sehingga fungsi ( ) menjadi
( ) ( ) ( ) ( ) ( )
Jika ( ) diminimumkan maka turunan (4.18) ke nol yaitu
( ) , (4.19) dari (4.19) diperoleh ( ) ( )
berdasarkan (2.26) dan gradien maka didapatkan
( )
Jadi untuk proses pencarian ukuran langkah pada metode steepest descent untuk kasus fungsi kuadratik dapat digunakan rumus (4.20), dimana adalah matriks simetrik dan definit positif.
17 Kekonvergenan Metode Steepest Descent
Teorema 4.3 (Konvergensi Global Metode Steepest Descent)
Misalkan . Untuk setiap titik akumulasi dari barisan iterasi * + yang dihasilkan dari Algoritme 4.1 dengan exact line search adalah titik stasioner. Bukti
Misalkan ̅ merupakan titik akumulasi dari * + dan adalah indeks terbatas sedemikian hingga ̅. Tetapkan ( ). Karena
maka barisan * | + terbatas seragam dan ‖ ‖ ‖ ( )‖. Karena asumsi Teorema 4.2 terpenuhi, maka ‖ ( ̅)‖ ini berarti bahwa ( ̅) . Teorema 4.4 (Konvergensi Global Metode Steepest Descent)
Misalkan ( ) terdiferensialkan dua kali pada dan ‖ ( )‖
untuk konstanta positif. Diberikan nilai awal dan . Maka untuk barisan yang dihasilkan dari Algoritme 4.1 terbatas dibanyak iterasi, atau
( ) atau ( ) Bukti
Perhatikan kasus yang tak terbatas, dari Algoritme 4.1 dan Teorema 4.1 diperoleh ( ) ( ) ‖ ( )‖ sehingga ( ) ( ) ∑, ( ) ( ∑‖ ( )‖
Dengan mengambil limit maka dihasilkan ( ) atau
‖ ( )‖ .
Teorema 4.5 (Laju Konvergensi Dari Metode Steepest Descent Untuk Kasus Fungsi Kuadratik)
Perhatikan masalah minimasi nirkendala berikut
( ) ( ) dimana adalah matriks simetris dan definit positif. Misalkan dan masing-masing adalah nilai eigen terbesar dan terkecil dari . Misalkan merupakan solusi dari masalah (4.21), maka barisan * + yang dihasilkan oleh metode steepest descent konvergen ke , dengan tingkat konvergen linear dan berlaku batas-batas berikut:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ‖ ‖ ‖ ‖ ( ) ( ) ‖ ‖ ‖ ‖ √ √ ( ) ( ) dimana ⁄ .
Bukti
Diketahui bentuk metode steepest descent (4.7) yaitu
Karena masalah pengoptimuman (4.21) berbentuk kuadratik maka dapat dituliskan dalam bentuk
dengan , sehingga ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )( )
Dengan menggunakan ketaksamaan Kantorovich (2.33) maka diperoleh
( ) ( ) [ ( ) ( )( )] ( ) [ ( ) ] ( ) terbukti untuk (4.22).
Selanjutnya akan dibuktikan untuk (4.23) dan (4.24). Misalkan
. Perhatikan bahwa merupakan matriks simetrik dan definit positif,
sehingga (4.26) jika maka ‖ ‖ ( ) (4.27) dari (4.26) diperoleh ‖ ‖ ( ) ‖ ‖ (4.28)
sehingga dari (4.25), (4.27) dan (4.28) diperoleh
‖ ‖ ‖ ‖ ‖ ‖ ‖ ‖ ( )
terbukti untuk (4.23) dan (4.24).
Teorema diatas berlaku juga untuk fungsi kuadratik dengan bentuk
( ) ( )
19 Metode Barzilai dan Borwein
Metode Barzilai dan Borwein atau disebut metode BB merupakan metode pengembangan dari metode steepest descent dengan mengganti ukuran langkah . Ide utama dari pendekatan metode BB adalah menggunakan informasi dalam iterasi sebelumnya untuk menentukan ukuran langkah dalam iterasi selanjutnya. Ukuran langkah metode BB diturunkan dari dua titik pendekatan ke garis potong persamaan yang didasari oleh metode Newton. Adapun metode Quasi-Newton yaitu sebagai berikut:
(4.30)
dimana dan adalah matriks identitas.
Misalnya diberikan ekspansi deret Taylor (2.32) dari fungsi real ( )
untuk pendekatan kuadratik yang terturunkan untuk semua tingkatan di sekitar titik yaitu
( ) ( ) ( ) ( ) ( ) ( ) dimana ( ) dan ( ). Misalnya ( ), jika (4.31) diturunkan terhadap maka
( ) ( )
Kemudian dimisalkan dan sehingga diperoleh
(4.32)
atau
(4.33)
Pertama akan dibahas masalah (4.32). Jika masalah (4.32) diselesaikan dengan menggunakan least-squares (kuadrat terkecil) maka akan diperoleh:
‖
‖
kemudian disederhanakan menjadi
〈 〉 〈 〉 〈 〉
Dari syarat perlu minimum lokal (Teorema 2.2) didapatkan
〈 〉 〈 〉 sehingga 〈 〉 〈 〉 Karena maka ( )
Jadi telah didapatkan ukuran langkah pertama (4.34) dari metode BB. Untuk masalah (4.33) akan dicari nilai
‖
‖
dengan cara penyelesaian yang sama pada masalah (4.32) maka diperoleh ukuran langkah yang kedua
Dari penyelesaian (4.32) dan (4.33) telah didapatkan dua ukuran langkah yang baru yaitu (4.34) dan (4.35). Kedua ukuran langkah ini merupakan ukuran langkah dari metode Barzilai dan Borwein yang memiliki langkah Q-super linear konvergensi pada tiga langkah berturut-turut (Dai 2003). Lebih jelasnya algoritme dari metode Barzilai dan Borwein dituliskan sebagai berikut:
Algoritme 4.2 Barzilai dan Borwein (BB)
Step 0. Diberikan titik awal dan batas toleransi . Tetapkan .
Step 1. Tentukan . Jika ‖ ‖ , berhenti. Jika tidak tentukan
.
Step 2. Jika k = 0 maka tentukan dengan exact line search. Jika tidak Tentukan dengan dimana dan Step 3. Hitung
Step 4. Beri nilai , dan pergi ke Step 1.
Metode Alternatif Minimisasi
Dalam beberapa pengertian, prinsipnya bahwa meminimumkan suatu fungsi
( ) yang kontinu dan terdiferensialkan dua kali (fungsi smooth) adalah setara dengan meminimumkan norm gradien ‖ ( )‖. Hal ini merupakan ide dasar dari metode gradien Alternatif Minimisasi (Dai dan Yuan 2003). Metode Alternatif Minimisasi (AM) adalah modifikasi metode steepest descent dengan ukuran langkah yang bergantian antara meminimumkan nilai fungsi dan norm gradien disepanjang garis steepest descent. Lebih tepatnya untuk dipilih ukuran langkah sehingga
*‖ ( )‖+ ( ) dan
* ( )+ ( ) Dapat dilihat bahwa gradien dari ‖ ( )‖ dan ( ) masing-masing adalah
( ) ‖ ( )‖⁄ dan ( ), sehingga dari (4.36) dan (4.37) diperoleh
(4.38)
dan
(4.39)
Dari hubungan di atas dapat simpulkan bahwa saling konjugat dengan , sedangkan dan saling ortogonal. Berdasarkan (4.7) dan didapatkan
21 { ( )
Dari ketaksamaan Cauchy dan asumsi bahwa matriks simetrik definit positif, diperoleh
* +
Hal ini menunjukkan bahwa ukuran langkah metode AM pada setiap iterasi ganjil lebih kecil atau sama dengan ukuran langkah dari metode SD, yaitu
(4.41) Untuk ukuran langkah pada iterasi genap jelas terlihat bahwa
(4.42) Dari hubungan (4.41) dan (4.42) menunjukkan bahwa metode AM melakukan langkah SD penuh setelah langkah SD yang diperpendek. Sebagai contoh diilustrasikan dalam Gambar 3 dengan persamaan
( ) .
/ . /
Dari Gambar 3 dapat dilihat dan merupakan iterasi yang dihasilkan oleh metode SD yang dimulai dari titik , sedangkan dan merupakan iterasi dari metode AM. Dapat dilihat bahwa ( )
( ) ( ) yang berarti bahwa metode AM adalah monoton. Terlihat dari Gambar 3 bahwa ( ) ( ) tetapi (
) (
). Meskipun
( ) ( ) tidak selalu berlaku untuk kasus fungsi konveks kuadratik.
𝐱 𝑘
𝐱𝟐𝒌𝑨𝑴
𝐱𝟐𝒌𝑺𝑫
𝐱𝟐𝒌 𝟏𝑺𝑫
𝐱𝟐𝒌 𝟏𝑨𝑴
Gambar 3 Ilustrasi perbandingan metode Alternatif Minimisasi dan metode steepest descent
Algoritme 4.3 Alternatif Minimisasi (AM)
Step 0. Diberikan titik awal dan batas toleransi . Tetapkan .
Step 1. Tentukan dan . Jika ‖ ‖ , berhenti. Step 2. Jika k ganjil maka tentukan
jika tidak tentukan
Step 3. Hitung
Step 4. Beri nilai , dan pergi ke Step 1.
Metode Yuan
Metode Yuan (Yuan 2006) menggunakan ukuran langkah yang bergantian seperti yang dilakukan pada metode AM. Akan tetapi metode Yuan menggunakan ukuran langkah yang baru. Untuk analisis pada metode Yuan, diasumsikan bahwa fungsi objektif adalah sebagai berikut:
( )
dimana dan simetris dan definit positif. Metode baru yang digunakan akan memberikan nilai minimum dari ( ) dengan melakukan iterasi. Dapat dilihat bahwa pencarian exact line harus dilakukan pada iterasi terakhir sebelum algoritme berhasil menemukan solusinya. Diasumsikan bahwa digunakan pencarian exact line pada iterasi pertama untuk mendapatkan keberuntungan apabila ada kasus dimana algoritme dapat menemukan solusi pada iterasi pertama. Oleh karena itu, dibuatlah algoritme sebagai berikut:
dimana dan didapat dari pencarian exact line dan adalah solusi. Perlu dicari formula untuk sehingga akan menjadi nilai minimum dari fungsi objektif.
Metode steepest descent adalah invarian dengan transformasi ortogonal. Untuk mempermudah analisis, dipelajari kasus dimana dan adalah dua buah sumbu. Sesuai dengan pencarian exact line pada iterasi pertama, gradien dan adalah ortogonal. Oleh karena itu untuk semua vektor dapat dituliskan sebagai kombinasi linear dari dan . Misalkan diberikan fungsi:
(
‖ ‖ ‖ ‖) (‖ ‖) . /
. / ( ⁄‖ ‖ ⁄‖ ‖‖ ‖
23 Berdasarkan pencarian exact line (4.20) pada iterasi pertama dan kedua, diperoleh
‖ ‖ , ‖ ‖ dan ‖ ‖ sehingga
(
‖ ‖ ‖ ‖) (‖ ‖) . /
. / ( ⁄ ‖ ‖ ⁄ ‖ ‖
‖ ‖ ⁄ ‖ ‖ ⁄ ) . /
Dari persamaan di atas, dapat diketahui nilai minimum dari fungsi objektifnya dengan ⁄ dan ⁄ , sehingga diperoleh masing-masing:
‖ ‖ ‖ ‖ (4.43)
dan
‖ ‖ ‖ ‖ ‖ ‖‖ ‖ (4.44)
Jika dilakukan eliminasi terhadap (4.43) dan (4.44) diperoleh
‖ ‖ ‖ ‖ ‖ ‖ ⁄ ‖ ‖ ⁄ dan ‖ ‖‖ ‖ ‖ ‖ ⁄ ‖ ‖ ⁄ Disederhanakan menjadi . / ‖ ‖‖ ‖ ‖ ‖ ‖ ‖ ( ‖ ‖ ‖ ‖)
Untuk mendapatkan ‖ ‖ ‖ ‖ , perlu diketahui bahwa arah gradien sejajar terhadap vektor residual . Untuk itu, diperlukan dua arah
. / ( ‖ ‖)
dan
(‖ ‖) ( ⁄ ‖ ‖ ⁄ ‖ ‖
‖ ‖ ⁄ ‖ ‖ ⁄ ) ( ‖ ‖)
yang merupakan dua arah yang sejajar. Dua arah tersebut masing-masing sejajar terhadap . ‖ ‖ ‖ ‖ (‖ ‖ ‖ ‖ ) ‖ ‖/ dan ( ‖ ‖ ‖ ‖ ) Diasumsikan bahwa . ‖ ‖ ‖ ‖ (‖ ‖ ‖ ‖ ) ‖ ‖/ ( ‖ ‖ ‖ ‖ ) ( )
untuk . Berdasarkan baris pertama persamaan (4.45) didapatkan ‖ ‖ . Kemudian nilai λ tersebut disubtitusikan ke baris kedua pada persamaan (4.45) sehingga diperoleh
( ‖ ‖
‖ ‖ )
Persamaan ini ekuivalen dengan
( ‖ ‖
( ‖ ‖) ) ( ) ( ) ( )
Karena definit positif, diketahui bahwa
‖ ‖
( ‖ ‖)
Dari persamaan (4.46) diperoleh dua solusi positif untuk yaitu :
( ⁄ ⁄ ) √( ⁄ ⁄ )
Dari dua solusi tersebut dipilih nilai yang lebih kecil dan dapat dituliskan sebagai berikut:
√( ⁄ ⁄ ) ‖ ‖ ⁄‖ ‖ ⁄ ⁄ ( )
dengan . inilah yang disebut ukuran langkah baru dan kemudian akan diaplikasikan ke dalam metode hasil modifikasi steepest descent. Untuk fungsi konveks kuadratik di n ( > 2) dimensi, berdasarkan (4.47) dapat dituliskan
√( ⁄ ⁄ ) ‖ ‖ ⁄‖ ‖ ⁄ ⁄
( )
Secara umum ukuran langkah dari metode Yuan adalah
,
( )
Algoritme 4.4 Yuan
Step 0. Diberikan titik awal dan batas toleransi . Step 1. Tentukan dan . Jika ‖ ‖ , berhenti. Tetapkan . Step 2. Tentukan . Kemudian hitung
Step 3. Jika ‖ ‖ , berhenti
Step 4. Tentukan dan . Tentukan
√( ⁄ ⁄ ) ‖ ‖ ⁄‖ ‖ ⁄ ⁄
Hitung
Step 5. Jika ‖ ‖ , berhenti
25 Modifikasi Metode Steepest Descent dengan Ukuran Langkah Baru
Telah dibahas pada sub-bab sebelumnya bahwa metode gradien Yuan menggunakan ukuran langkah dengan exact line search pada iterasi ganjil dan kemudian menggunakan ukuran langkah (4.48) pada iterasi genap yang secara umum dituliskan seperti pada (4.49). Berdasarkan metode Yuan ini maka akan dilakukan modifikasi ukuran langkah dengan dua ukuran langkah yang baru. Untuk ukuran langkah yang pertama akan dibentuk suatu algoritme dengan ide langkah sebagai berikut:
(4.50)
dimana dan merupakan ukuran langkah dengan proses pencarian menggunakan exact line search, sedangkan untuk dan menggunakan ukuran langkah Yuan (4.48). Algoritme (4.50) ini merupakan bentuk awal dari proses iterasi, sehingga untuk proses iterasi (4.50) selanjutnya akan terus berlanjut sampai solusi nilai ditemukan. Secara umum ukuran langkah dari bentuk (4.50) dapat dituliskan sebagai berikut:
,
( )
( ) ( )
Algoritme 4.5 Ukuran Langkah Baru (a)
Step 0. Diberikan titik awal dan batas toleransi . Tetapkan .
Step 1. Tentukan dan . Jika ‖ ‖ , berhenti. Step 2. Jika mod(k,4) = 0 atau 1 maka tentukan
jika tidak tentukan dan
√( ⁄ ⁄ ) ‖ ‖ ⁄‖ ‖ ⁄ ⁄
Step 3. Hitung
Step 4. Beri nilai , dan pergi ke Step 1.
Untuk ukuran langkah baru yang kedua dapat dibuat algoritme dengan ide langkah sebagai berikut:
(4.52)
dimana dan merupakan ukuran langkah dengan proses pencarian menggunakan exact line search, sedangkan untuk dan menggunakan ukuran langkah Yuan. Sama halnya proses iterasi pada (4.50) proses iterasi pada
(4.52) pula akan terus berlanjut sampai solusi nilai ditemukan. Secara umum ukuran langkah dari bentuk (4.52) dapat dituliskan sebagai berikut:
,
( )
( ) ( )
Algoritme 4.6 Ukuran Langkah Baru (b)
Step 0. Diberikan titik awal dan batas toleransi . Tetapkan .
Step 1. Tentukan dan . Jika ‖ ‖ , berhenti. Step 2. Jika mod(k,4) = 1 atau 2 maka tentukan
Jika tidak tentukan dan
√( ⁄ ⁄ ) ‖ ‖ ⁄‖ ‖ ⁄ ⁄
Step 3. Hitung
Step 4. Beri nilai , dan pergi ke Step 1.
Hasil Numerik
Pada sub-bab ini dilakukan perbandingan hasil numerik dari setiap metode gradien yang telah dijelaskan pada sub-bab sebelumnya, yaitu SD, BB, AM, Yuan, Algoritme 4.5 dan Algoritme 4.6. Sintaks dari setiap metode dapat dilihat pada Lampiran 1. Ukuran langkah untuk metode SD menggunakan (4.20) yang merupakan penyederhanaan dari exact line search. Untuk metode BB dibagi menjadi dua bagian, yaitu BB1 menggunakan ukuran langkah (4.34) dan BB2 menggunakan ukuran langkah (4.35). Perbandingan dilakukan untuk kasus fungsi nonlinear dengan bentuk kuadratik. Fungsi kuadratik yang digunakan dalam penelitian ini dibangkitkan secara acak dalam bentuk
( ) ( ) ( )( )
menyatakan dimensi dari fungsi kuadratik dengan
. vektor ( ) merupakaan bilangan acak integer pada
interval , -. Selanjutnya dan merupakan kondisi dari matriks Hesse dari fungsi. Kemudian ( ) adalah bilangan acak integer pada interval , -. Untuk semua dimensi dan diberikan titik awal vektor nol ( ) dan kriteria penghentian adalah ‖ ‖ . Percobaan dilakukan sebanyak 5 kali untuk setiap dimensi dan setiap dari setiap metode. Sehingga percobaan yang dilakukan untuk satu dimensi sebanyak 105 kali dan total percobaan untuk semua dimensi sebanyak 1260 kali (Lampiran 2). Rata-rata jumlah iterasi dan running time dari percobaan disajikan pada tabel.
27 Tabel 1 Rata-rata jumlah iterasi dari metode steepest descent
n λn
Rata-rata jumlah iterasi
SD BB1 BB2 AM Yuan (4.5) (4.6) 2 10 15.8 9.4 8.8 7.8 3.0 4.0 5.0 100 17.6 10.2 9.4 8.0 3.0 4.0 5.0 1000 18.0 9.6 8.2 6.6 3.0 4.0 5.0 3 10 58.0 16.0 15.4 21.6 15.0 12.4 14.8 100 446.0 19.4 15.0 41.2 9.4 9.2 11.4 1000 ** 25.2 14.8 63.2 7.0 8.0 10.6 10 10 71.2 28.8 28.4 36.2 34.0 26.6 26.6 100 572.2 73.4 59.0 82.8 77.2 55.4 50.8 1000 ** 84.4 62.4 177.6 215.8 66.4 49.8 20 10 69.8 28.8 31.4 39.2 33.4 27.2 28.8 100 611.8 66.2 63.6 87.6 92.6 53.2 63.0 1000 ** 129.0 102.0 250.4 256.6 90.0 101.2 30 10 74.4 29.2 30.8 38.4 32.2 27.4 29.8 100 618.0 81.8 84.0 94.8 119.6 67.2 78.4 1000 ** 161.2 90.4 214.0 372.2 117.6 96.2 40 10 71.0 31.4 31.4 40.2 30.8 29.2 27.8 100 619.8 85.8 81.0 95.6 124.6 72.8 72.4 1000 ** 158.8 121.4 234.0 559.0 138.4 116.0 50 10 70.4 30.4 29.8 40.4 33.6 28.8 26.0 100 568.4 83.0 81.4 92.6 105.8 69.6 73.0 1000 ** 169.6 127.2 256.0 741.4 115.2 123.6 60 10 73.0 32.0 30.6 38.0 32.8 30.6 25.6 100 541.8 83.6 79.6 91.6 107.8 69.8 69.6 1000 ** 153.0 125.0 209.2 431.4 126.8 120.2 70 10 72.0 30.0 29.8 38.8 32.2 28.4 28.0 100 588.3 98.2 84.2 103.2 114.6 77.4 81.8 1000 ** 174.8 122.0 321.0 514.2 127.8 129.2 80 10 73.4 32.6 30.2 39.4 32.8 28.2 27.0 100 597.8 86.0 90.2 110.0 114.2 77.6 78.2 1000 ** 151.6 133.4 236.6 631.0 132.2 126.6 90 10 73.6 32.2 31.4 39.4 32.8 28.2 25.4 100 671.2 94.4 87.8 105.0 127.8 79.8 80.6 1000 ** 160.0 147.0 249.6 676.8 128.0 133.0 100 10 73.2 32.6 30.8 39.2 34.2 29.2 26.8 100 566.6 85.2 80.2 93.6 113.6 77.0 74.8 1000 ** 170.6 146.8 261.8 540.2 139.4 137.8
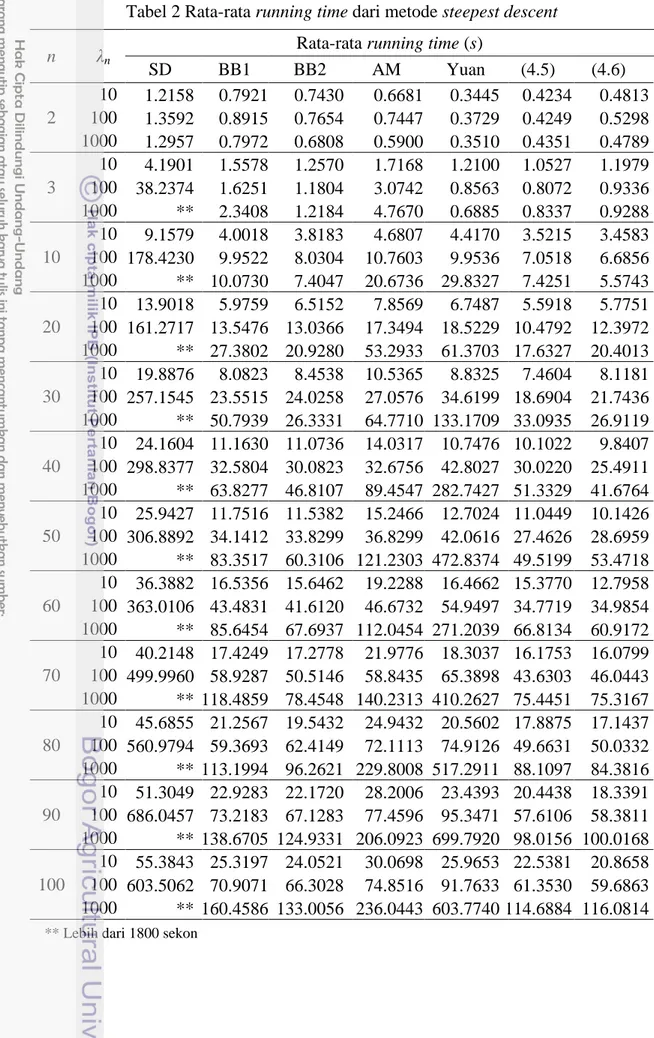
Tabel 2 Rata-rata running time dari metode steepest descent n λn
Rata-rata running time (s)
SD BB1 BB2 AM Yuan (4.5) (4.6) 2 10 1.2158 0.7921 0.7430 0.6681 0.3445 0.4234 0.4813 100 1.3592 0.8915 0.7654 0.7447 0.3729 0.4249 0.5298 1000 1.2957 0.7972 0.6808 0.5900 0.3510 0.4351 0.4789 3 10 4.1901 1.5578 1.2570 1.7168 1.2100 1.0527 1.1979 100 38.2374 1.6251 1.1804 3.0742 0.8563 0.8072 0.9336 1000 ** 2.3408 1.2184 4.7670 0.6885 0.8337 0.9288 10 10 9.1579 4.0018 3.8183 4.6807 4.4170 3.5215 3.4583 100 178.4230 9.9522 8.0304 10.7603 9.9536 7.0518 6.6856 1000 ** 10.0730 7.4047 20.6736 29.8327 7.4251 5.5743 20 10 13.9018 5.9759 6.5152 7.8569 6.7487 5.5918 5.7751 100 161.2717 13.5476 13.0366 17.3494 18.5229 10.4792 12.3972 1000 ** 27.3802 20.9280 53.2933 61.3703 17.6327 20.4013 30 10 19.8876 8.0823 8.4538 10.5365 8.8325 7.4604 8.1181 100 257.1545 23.5515 24.0258 27.0576 34.6199 18.6904 21.7436 1000 ** 50.7939 26.3331 64.7710 133.1709 33.0935 26.9119 40 10 24.1604 11.1630 11.0736 14.0317 10.7476 10.1022 9.8407 100 298.8377 32.5804 30.0823 32.6756 42.8027 30.0220 25.4911 1000 ** 63.8277 46.8107 89.4547 282.7427 51.3329 41.6764 50 10 25.9427 11.7516 11.5382 15.2466 12.7024 11.0449 10.1426 100 306.8892 34.1412 33.8299 36.8299 42.0616 27.4626 28.6959 1000 ** 83.3517 60.3106 121.2303 472.8374 49.5199 53.4718 60 10 36.3882 16.5356 15.6462 19.2288 16.4662 15.3770 12.7958 100 363.0106 43.4831 41.6120 46.6732 54.9497 34.7719 34.9854 1000 ** 85.6454 67.6937 112.0454 271.2039 66.8134 60.9172 70 10 40.2148 17.4249 17.2778 21.9776 18.3037 16.1753 16.0799 100 499.9960 58.9287 50.5146 58.8435 65.3898 43.6303 46.0443 1000 ** 118.4859 78.4548 140.2313 410.2627 75.4451 75.3167 80 10 45.6855 21.2567 19.5432 24.9432 20.5602 17.8875 17.1437 100 560.9794 59.3693 62.4149 72.1113 74.9126 49.6631 50.0332 1000 ** 113.1994 96.2621 229.8008 517.2911 88.1097 84.3816 90 10 51.3049 22.9283 22.1720 28.2006 23.4393 20.4438 18.3391 100 686.0457 73.2183 67.1283 77.4596 95.3471 57.6106 58.3811 1000 ** 138.6705 124.9331 206.0923 699.7920 98.0156 100.0168 100 10 55.3843 25.3197 24.0521 30.0698 25.9653 22.5381 20.8658 100 603.5062 70.9071 66.3028 74.8516 91.7633 61.3530 59.6863 1000 ** 160.4586 133.0056 236.0443 603.7740 114.6884 116.0814
29
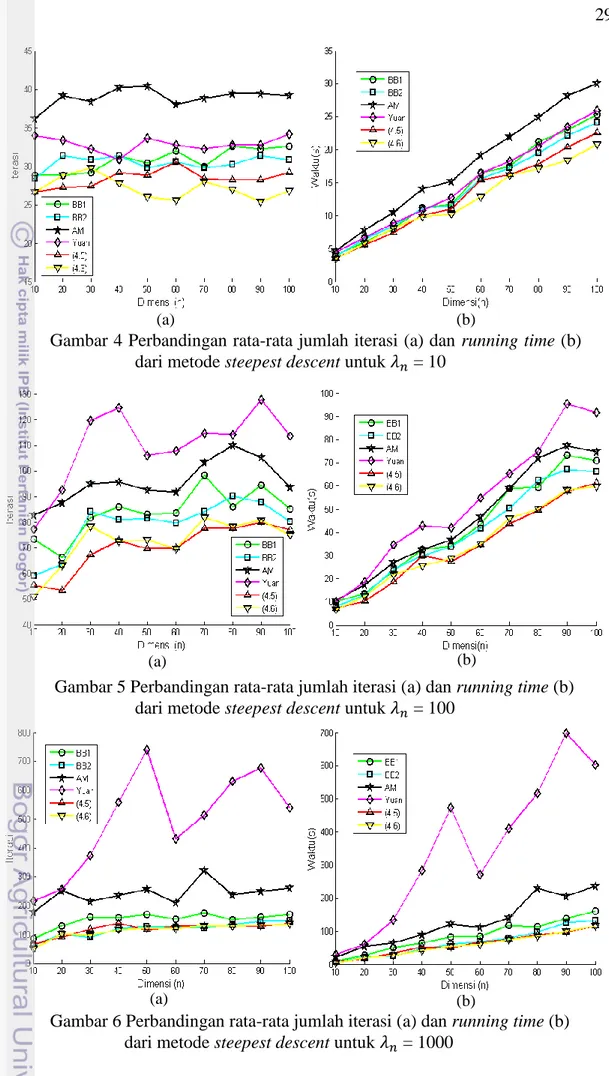
Gambar 4 Perbandingan rata-rata jumlah iterasi (a) dan running time (b) dari metode steepest descent untuk = 10
Gambar 5 Perbandingan rata-rata jumlah iterasi (a) dan running time (b) dari metode steepest descent untuk = 100
Gambar 6 Perbandingan rata-rata jumlah iterasi (a) dan running time (b) dari metode steepest descent untuk = 1000
(a) (b)
(a) (b)
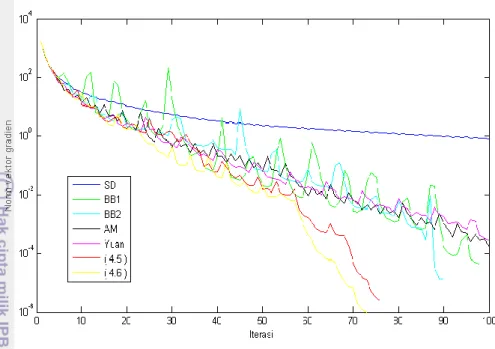
Gambar 7 Kekonvergenan dari metode steepest descent
Berdasarkan hasil percobaan yang dilakukan secara umum dapat dilihat hubungan antara dimensi dan dengan iterasi dan running time. Untuk kasus dimensi kecil (n = 2 & 3) dapat dilihat bahwa besarnya tidak berpengaruh terhadap iterasi dan running time. Artinya semakin besar tidak menjamin bahwa iterasi dan running time akan semakin besar pula (Tabel 1 dan 2). Untuk kasus dimensi besar (n = 10, 20, 100) terlihat bahwa semakin besar maka semakin besar pula iterasi dan running timenya (Gambar 4 – 6). Selanjutnya dapat dilihat bahwa semakin besar dimensi tidak menyebabkan semakin besar iterasinya (Gambar 4a – 6a). Berbeda halnya dengan running time, semakin besar dimensi maka semakin besar pula running timenya (Gambar 4b – 6b).
Pada masalah fungsi kuadratik dengan dimensi yang kecil untuk semua (10,100,1000), dapat dilihat bahwa metode Yuan mampu menemukan solusi nilai minimum dengan iterasi dan running time yang terkecil. Meskipun demikian bahwa Algoritme (4.5) dan (4.6) mampu menyeimbangi kecepatan metode Yuan untuk dimensi yang kecil. Untuk kasus dengan dimensi besar, metode Yuan memberikan hasil yang buruk khususnya pada dan . Berbeda dengan Algoritme (4.5) dan (4.6), untuk kasus dimensi besar dengan semua ukuran , Algoritme (4.5) dan (4.6) lebih dominan menemukan solusi nilai minimum fungsi dengan iterasi dan running time yang terkecil dibandingkan dari metode BB, AM, dan Yuan (Gambar 4 – 6). Hal ini terjadi karena Algoritme (4.5) dan (4.6) memiliki tingkat konvergensi yang lebih cepat dibandingkan dengan metode gradien lainnya, sebagai contoh ditunjukkan pada Gambar 7 dengan n = 100 dan = 100. Meskipun demikian pada dimensi dan tertentu metode BB dapat mengungguli Algoritme (4.5) dan (4.6).