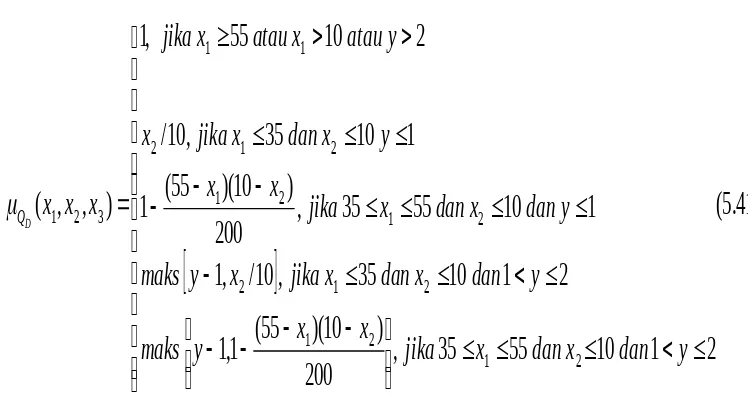makalah bab 5 fuzzy dwi purnomo arjudin ok 1

TUGAS KELOMPOK

MATAKULIAH FUZZY THEORY

CHAPTER 5

LINGUISTIC VARIABLES ANDFUZZY IF-THEN RULES

(VARIABEL-VARIABEL LINGUISTIK DAN ATURAN FUZZY JIKA- MAKA)

Makalah Diskusi Kelas

Buku Sumber

A COURSE IN FUZZY SYSTEMS AND CONTROL Oleh Li-Xin Wang

Dosen Pembina:

Prof. Dr. Toto Nusantara, M.Si. Dr. Hery Susanto, M.Si.

Kelompok 4

Arjudin:NPM. 130311910786Dwi Purnomo:NPM. 130311910784

PROGRAM STUDI PENDIDIKAN MATEMATIKA S-3

PROGRAM PASCASARJANA

BAB 5

VARIABEL-VARIABEL LINGUISTIK DAN ATURAN FUZZY JIKA-MAKA 5.1 Dari Variabel Numerik ke Variabel Linguistik

Dalam kehidupan kita sehari-hari, kata-kata sering digunakan untuk menggambarkan variabel. Sebagai contoh jika kita mengatakan "hari ini panas," maka sama artinya dengan, "suhu saat ini tinggi," kita menggunakan kata "tinggi" untuk menggambarkan variabel "suhu hari ini." Artinya, variabel "suhu hari ini“ mengambil kata "tinggi" sebagai nilainya. Jelas, variabel "suhu hari ini" juga dapat diganti bilangan seperti 25°C, 19°C, dan seterusnya, sebagai nilai-nilainya. Ketika variabel diganti bilangan sebagai nilainya, kita mempunyai kerangka kerja matemtika yang tersusun dengan baik untuk merumuskannya. Tetapi ketika variabel mengambil kata-kata sebagai nilainya, kita tidak dapat merumuskannya dalam teori matematika klasik. Untuk itu konsep variabel linguistik perlu diperkenalkan. Dengan kata lain, jika variable-variabel yang digunakan mengambil kata-kata dalam bahasa sehari-hari sebagai nilai-nilainya, hal itulah yang disebut variabel linguistik. Pertanyaannya adalah adalah bagaimana merumuskan kata-kata dalam istilah matematika? Dalam hal ini kita akan menggunakan himpunan fuzzy untuk menggambarkan kata-kata.

Definisi 5.1.

Jika suatu variabel dapat digambarkan dengan kata-kata dalam bahasa sehari-hari sebagai nilai-nilainya, variabel ini disebut variabel linguistik, di mana kata-kata yang dicirikan dengan himpunan fuzzy didefinisikan dalam semesta pembicaraan dalam suatu variabel yang terdefinisi.

Contoh 5.1.

Kecepatan sebuah mobil adalah variabel x yang nilainya berada dalam interval [0,

Vmax], dalam hal ini Vmax adalah kecepatan maksimum mobil. Kita dapat

mendefinisikan kecepatan mobil dalam tiga himpunan fuzzy "lambat", "menengah", dan "cepat" dalam [0, Vmax] seperti ditunjukkan pada Gambar 5.1. Jika kita

adalah menengah”, dan “

x

adalah cepat”. Tentu saja, x juga dapat dinyatakan dengan bilangan dalam interval [0, Vmax] sebagai nilai-nilainya, misalnya, x = 50

km/jam, x = 25 km/jam dan seterusnya.

Definisi 5.1 merupakan definisi sederhana dan intuitif untuk variabel linguistik. Dalam literatur teori fuzzy, definisi yang lebih formal tentang variabel linguistik yang biasanya digunakan (Zadeh [I973] dan [1975]). Definisi tersebut diberikan sebagai berikut.

Definisi 5.2.

Suatu variabel linguistik ditandai dengan huruf-huruf (X, T, U, M), di mana:

1) X adalah nama dari variabel linguistik, dalam Contoh 5.1, X adalah kecepatan mobil.

2) T adalah himpunan nilai linguistik yang diambil X, dalam Contoh 5.1,

T = {lambat, menengah, cepat).

3) U adalah domain fisik yang sebenarnya di mana variabel linguistik X mengambil nilai kuantitatif yang tegas; dalam Contoh 5.1, U = [0, Vmax].

4) M adalah aturan semantik yang berhubungan dengan setiap nilai linguistik di T

dengan suatu himpunan fuzzy di U; dalam Contoh 5.1, M menghubungkan "lambat", "menengah," dan "cepat" dengan fungsi keanggotaan yang ditunjukkan pada Gambar. 5.1.

perluasan dari variabel numerik dalam arti bahwa mereka diperbolehkan untuk mengambil himpunan fuzzy sebagai nilai-nilai mereka, lihat Gambar. 5.2.

Mengapa konsep variabel linguistik penting? Karena variabel linguistik adalah unsur-unsur yang paling mendasar dalam representasi pengetahuan manusia. Ketika kita menggunakan sensor untuk mengukur variabel, mereka memberi kita bilangan, ketika kita meminta mereka untuk mengevaluasinya, mereka memberi kita kata-kata. Sebagai contoh, ketika kita menggunakan spedometer untuk mengukur kecepatan mobil, tertera bilangan seperti 39 km/jam, 42 km/jam, ketika kita meminta manusia untuk memberitahu kita tentang kecepatan mobil, dia sering memberitahu dalam kata-kata seperti "itu lambat," "itu cepat," dan seterusnya. Oleh karena itu, dengan memperkenalkan konsep variabel linguistik, kita dapat mendeskripsikan rumusan yang samar-samar dalam bahasa alami ke dalam istilah matematika yang tepat. Ini adalah langkah pertama untuk menggabungkan pengetahuan manusia ke dalam sistem teknik secara sistematis dan efisien.

5.2 Linguistic Hedges (Batasan-batasan Linguistik)

tunggal (atomic terms) x₁,x₂, x_3,x₄,x₅,x₆,...,x_n₁,x_n.Suku–suku tunggal dapat diklasifikasikan ke dalam tiga kelompok:

1) Istilah dasar (Primary terms), yang merupakan label dari fuzzy set; dalam Contoh 5.1, adalah “lambat," "menengah," dan "cepat."

2) Komplemen "tidak" dan hubungan "dan" dan "atau."

3) Hedges, seperti "sangat," sedikit," "lebih atau kurang," dan lain-lain.

Istilah "tidak," "dan," dan "atau" dipelajari dalam Bab 2 dan 3. Tugas kita sekarang adalah untuk mengkarakterisasi hedges.

Meskipun dalam penggunaan sehari-hari hedges sangat tidak memiliki arti yang terdifinisi denganjelas, pada dasarnya itu bertindak sebagai suatu penguat. Dalam kesempatan ini, kita memiliki definisi berikut untuk dua nilai hedges yang paling sering digunaka, yaitu sangatdan lebih atau kurang.

Definisi 5.3.

Misalkan A adalah himpunan fuzzy dalam U, maka sangat A didefinisikan sebagai himpunan fuzzy dalam U dengan fungsi keanggotaan





2

) ( )

(x A x

A

sangat 

  (5.1)

dan lebih atau kurang A adalah himpunan fuzzy dalam U dengan fungsi keanggotaan





1/2

) ( )

(x _A x

A kurang atau

lebih 

  (5.2)

Contoh 5.2

Misal U = {1,2, ..., 5) dan himpunan fuzzy kecil didefinisikan sebagai

Maka, menurut (5.1) dan (5.2) diperoleh

5.3 Aturan Fuzzy IF-THEN (Jika…maka)

Dalam Bab 1 telah disebutkan bahwa dalam sistem dan kontrol fuzzy, pengetahuan manusia dinyatakan dalam aturan fuzzy IF-THEN. Sebuah aturan fuzzy IF-THEN adalah pernyataan kondisional/implikasi yang diungkapkan sebagai

JIKA <proposisi fuzzy>, MAKA <proposisi fuzzy> (5.7) Oleh karena itu, dalam rangka memahami aturan fuzzy IF-THEN, pertama kita harus mengetahui apa yang dimaksud proposisi fuzzy.

5.3.1 Proposisi Fuzzy

Ada dua jenis proposisi fuzzy yaitu proposisi fuzzy tunggal, dan proposisi fuzzy majemuk.

A adalah

x _(5.8)

Suatu proposisi fuzzy tunggal adalah pernyataan tunggal di mana x adalah variabel linguistik, dan A adalah nilai linguistik dari x (yaitu, A adalah sebuah himpunan fuzzy yang didefinisikan dalam physical domainx). Suatu proposisi fuzzy majemuk adalah komposisi dari proposisi-proposisi fuzzy tunggal menggunakan penghubung

"dan," "atau," dan "tidak" yang merupakan irisan fuzzy, gabungan fuzzy, dan

komplemen fuzzy. Sebagai contoh, jika x merupakan kecepatan mobil pada Contoh 5.1, maka berikut ini adalah proposisi fuzzy (tiga pertama adalah proposisi fuzzy tunggal dan tiga terakhir adalah proposisi fuzzy majemuk):

di mana S, M dan F masing–masing melambangkan fuzzy set "lambat", "menengah," dan "cepat,".

Perhatikan bahwa dalam proposisi fuzzy majemuk, proposisi fuzzy tunggal independen, yaitu, x dalam beberapa proposisi pada (5.12) - (5.14) dapat berbeda variabel. Sebenarnya, variabel linguistik dalam proposisi fuzzy majemuk secara umum tidak sama. Sebagai contoh, misalkan x kecepatan mobil dan 

x

y adalah

percepatan mobil, maka jika kita mendefinisikan himpunan fuzzy besar (L) untuk percepatan tersebut, berikut adalah proposisi fuzzy majemuk

x adalah F dan y adalah L.

Oleh karena itu, proposisi fuzzy majemuk harus dipahami sebagai relasi fuzzy. Bagaimana menentukan fungsi keanggotaan untuk relasi fuzzy?

 Untuk penghubung "dan" menggunakan irisan fuzzy.

Secara khusus, misalkan x dan y variabel linguistik pada domain fisik U dan V, serta A dan B adalah himpunan fuzzy di U dan V, maka proposisi fuzzy majemuk

B adalah y

dan A adalah

x _(5,15)

diartikan sebagai relasi fuzzy A ∩ B di U



V dengan fungsi keanggotaan



( ), ( )



) ,

(x y t A x B y

B

A  

   (5.16)

x adalah S (5.9)

x adalah M (5.10)

x adalah F (5.11)

x adalah S atau x adalah bukan M (5.12)

x adalah S dan x adalah bukan F (5.13)

dimana t : [0, 1] x [0, 1] → [0, 1] adalah suatu t-norm.

 Untuk penghubung "atau" menggunakan gabungan fuzzy. Secara khusus, proposisi fuzzy majemuk

B adalah y

atau A adalah

x _(5.17)

diartikan sebagai relasi fuzzy A B di U



V dengan fungsi keanggotaan



( ), ( )



) ,

(x y s A x B y

B

A  

 _  _(5.18)

dimana s : [0, 1] x [0, 1] → [0, 1] adalah suatu s-norm.

 Untuk penghubung "tidak" menggunakan komplemen Fuzzy. Artinya, mengganti

tidak A dengan ,yang didefinisikan sesuai dengan operator komplemen dalam Bab 3.

Contoh 5.3.

Proposisi Fuzzy (5.14), yaitu,

FP = (x adalah S dan x tidak F) atau x adalah M (5,19) adalah suatu relasi fuzzy dalam ruang hasil kali [0, Vmax ]3 dengan fungsi keanggotaan



( ), ( ( ))



, ( )} {

) , ,

(x1 x2 x3 s t S x1 c F x2 M x3

FP   

  _(5.20)

di mana s, t dan c adalah s-norma, t-norm dan operator fuzzy complement, masing-masing, fuzzy set S = lambat, M = menengah, dan F = cepat didefinisikan pada Gambar. 5.1, dan x1 = x2 = x3 = x. Kami sekarang siap untuk menafsirkan aturan

fuzzy IF-THEN dalam bentuk (5.7).

5.3.2 Interpretasi aturan Fuzzy IF-THEN

Karena proposisi fuzzy ditafsirkan sebagai relasi-relasi fuzzy, pertanyaan kunci yang tersisa adalah bagaimana menafsirkan operasi IF-THEN. Dalam proposional kalkulus

didefinisikan oleh Tabel 5.1, di mana p dan q adalah variabel proposisi dengan nilai benar (T) atau salah (F).

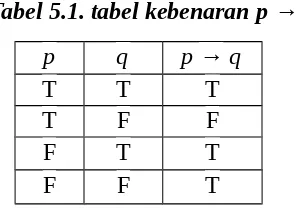
Tabel 5.1. tabel kebenaran p → q

p q p → q

T T T

T F F

F T T

F F T

Berdasarkan tabel 5.1 di atas kita melihat bahwa jika p dan q keduanya bernilai

benar atau salah, maka p q bernilai benar, jika p benar dan q salah, maka p q

bernilai salah, dan, jika p salah dan q benar, maka p q bernilai benar. Oleh karena

itu, p q adalah equivalent dengan

q (5.21)

dan

(p q) (5.22)

dalam arti bahwa mereka memiliki tabel kebenaran yang sama pada (Tabel 5.1)

sebagai p q di mana dan masing–masing mewakili operasi logika (klasik) "tidak," "atau," dan "dan".

Karena aturan fuzzy IF-THEN dapat dipandang sebagai mengganti p dan q

dengan proposisi fuzzy, kita dapat menafsirkan aturan fuzzy IF-THEN dengan

mengganti operator dan di (5.21) dan (5.22) sebagai fuzzy complement,

fuzzy unions, dan fuzzy intersections. Karena ada berbagai macam operator fuzzy complement, fuzzy union, dan fuzzy intersections, sejumlah interpretasi yang berbeda dariaturan Fuzzy IF-THEN yang diusulkan dalam literatur.

Berikut ini kita tulis ulang (5.7) sebagai IF <FP1> THEN <FP2> dan

adalah proposisi fuzzy. Diasumsikan bahwa FP1 adalah relasi fuzzy didefinisikan

dalam U = Ul



. . .



Un , dan FP2 adalah relasi fuzzy didefinisikan dalam V = Vl



. . .



Vm, serta x dan y masing-masing adalah variabel linguistik (vektor) di U dan

V.

Terdapat beberapa interprestasi aturan fuzzy JIKA-MAKA, yaitu:

1) Implikasi Dienes-Rescher: Jika kita mengganti operator logika dan V di (5.21) oleh komplemen fuzzy dasar (3.1) dan union fuzzy dasar (3.2), maka kita mendapatkan apa yang disebut implikasi Dienes-Rescher. Secara khusus, fuzzy IF-THEN aturan IF <FP1> THEN <FP2> ditafsirkan sebagai relasi fuzzy QD di

U



V dengan fungsi keanggotaan



1 ( ), ( )



max )

,

(x y FP₁ x FP₂ y

Q_D  

  

(5.23)

2) Implikasi Lukasiewicz: Jika kita menggunakan Yager s-norm (3.10) dengan w = 1 untuk V dan komplemen fuzzy dasar (3.1) untuk pada (5.21), kita

memperoleh implikasi Lukasiewicz . Secara khusus, fuzzy IF-THEN aturan IF <FP1> THEN <FP2> ditafsirkan sebagai relasi fuzzy QL di U



V dengan

fungsi keanggotaan



1,1 ( ) ( )



min ) ,

(x y FP₁ x FP₂ y

Q_L  

    _(5,24)

3) Implikasi Zadeh: Berikut fuzzy IF-THEN aturan IF <FP1> THEN <FP2>

ditafsirkan sebagai relasi fuzzy QZ di U



V dengan fungsi keanggotaan

_{( , ) max}



_{min( ( ), ( )),1 ( )}



1 2

1 x y x

y

x _{FP FP FP}

QZ   

   _(5.25)

Jelas, (5.25) diperoleh dari (5.22) dengan menggunakan komplemen fuzzy dasar (3.1), union fuzzy dasar (3.2), dan intersections fuzzy dasar (3.3) untuk

masing-masing , V dan

∧

.

4) Implikasi Godel: Implikasi Godel adalah formula implikasi terkenal dalam logika klasik. Dengan generalisasi ke proposisi fuzzy, dihasilkan aturan fuzzy

IF <FP1> THEN <FP2> yang ditafsirkan sebagai relasi fuzzy QG di U



V

)26

Adalah hal yang menarik untuk mengeksplorasi hubungan antara implikasi– implikasi di atas. Lemma berikut menunjukkan bahwa implikasi Zadeh lebih kecil dari implikasi Dienes-Rescher dan lebih kecil dari implikasi Lukasiewicz.

Lemma 5.1.

membahasnya dalam Bab 7-10. Pertanyaan lain adalah: Apakah (5.21) dan (5.22)

masih "ekuivalen" untuk p q saat p dan q adalah proposisi fuzzy dan apa artinya

"ekuivalen"? Sekarang kita mencoba untuk menjawab pertanyaan ini. Ketika p dan

q adalah proposisi yang tegas (yaitu, p dan q adalah benar atau salah), p q adalah implikasi global (global implications) dalam arti bahwa Tabel 5.1 mencakup semua

kemungkinan kasus. Namun, ketika p dan q adalah proposisi fuzzy, p q hanya

mungkin implikasi lokal (local implications) dalam arti bahwa p q memiliki nilai kebenaran besar hanya ketika kedua p dan q memiliki nilai kebenaran yang besar. Misalnya, ketika kita mengatakan "JIKA kecepatan tinggi, MAKA resistensi tinggi," kita hanya peduli dengan situasi lokal dalam arti bahwa aturan ini tidak memberitahu kita tentang situasi ketika "kecepatan lambat," "kecepatan menengah," dll. Oleh karena itu, aturan fuzzy IF-THEN

IF <FP1> THEN <FP2> (5.28)

harus ditafsirkan sebagai

IF <FP1> THEN <FP2>ELSE <NOTHING> (5.29)

di mana NOTHING berarti bahwa aturan ini tidak berlaku. Dalam hal logika, itu menjadi

p q= p

∧

q (5.30)

Dengan menggunakan min atau algebraic product untuk

∧

dalam (5.30), kita memperoleh implikasi Mamdani.

5) Implikasi Mamdani: aturan fuzzy IF-THEN (5.28) ditafsirkan sebagai hubungan fuzzy QMM atau QMP di U



V dengan fungsi keanggotaan



( ), ( )



(5.31)

min ) ,

(x y _FP1 x _FP2 y

MM

Q









atau

) 32 . 5 ( ) ( ) ( )

,

(x y FP₁ x FP₂ y

QMP  

 

IF-THEN bersifat lokal. Namun, seseorang mungkin tidak setuju dengan argumen ini. Sebagai contoh, seseorang mungkin berpendapat bahwa ketika kita mengatakan "JIKA kecepatan tinggi, MAKA resistensi tinggi," secara implisit menunjukkan bahwa "JIKA kecepatan lambat, MAKA resistensi rendah." Dalam pengertian ini, aturan Fuzzy IF-THEN adalah nonlokal. Perdebatan semacam ini menunjukkan bahwa ketika kita merepresentasikan pengetahuan manusia dalam aturan fuzzy IF-THEN, orang yang berbeda memiliki interpretasi yang berbeda. Akibatnya, implikasi yang berbeda diperlukan untuk mengatasi keragaman interpretasi. Misalnya, jika manusia ahli berpikir bahwa aturan mereka adalah lokal, maka implikasi Mamdani harus digunakan, jika tidak, implikasi global (5.23) - (5.26) harus dipertimbangkan.

Kita sekarang meninjau beberapa contoh untuk perhitungan QD, QL, QZ, QMM

dan QMP.

Contoh 5.4.

Misalkan x1 kecepatan mobil, x2 percepatan, dan y gaya yang diterapkan untuk pedal

gas. Tinjau aturan fuzzy IF-THEN berikut:

dan "besar" adalah himpunan fuzzy dalam domain kekuatan diterapkan pada pedal gas dengan fungsi keanggotaan

)36.

masing-masing. Jika kita menggunakan produk aljabar untuk t-norm dalam (5.16), maka proposisi fuzzy

FP1 = x1 adalah lambat dan x2 adalah kecil (5.37)

adalah relasi fuzzy dalam U1



U2 dengan fungsi keanggotaan



x

_{slow small}

FP





Gambar. 5.3 menggambarkan bagaimana untuk menghitung FP1 (x1, x2).

Jika kita menggunakan implikasi Dienes-Rescher (5.23), maka aturan fuzzy IF-THEN (5.33) ditafsirkan sebagai relasi fuzzy QD (x1, x2, y) di U1



U2



V dengan

Dari 5.38 didapat



 _{dari (5.36) dengan menggunakan operator max, kami menggambarkan}

pada Gambar 5.4 pembagian daerah 1 FP2(x1,x2)

Untuk implikasi Lukasiewicz, Zadeh dan Mamdani, kita dapat menggunakan prosedur yang sama untuk menentukan fungsi keanggotaan.

perhitungan dari fungsi keanggotaan akhir QD, QZdan lain–lain, adalah tidak

praktis, meskipun langsung. Sebuah cara untuk mengatasi kompleksitas ini adalah dengan menggunakan fungsi mulus tunggal untuk mendekati fungsi nonsmooth; lihat contoh berikut.

Contoh 5.4 (lanjutan)

Andaikan kita menggunakan

5 implikasi Mamdani (5.32) dan hasil aljabar untuk t-norm pada (5.16), maka fungsi

keanggotaanQ_MP(x1,x2,y)dapat dihitung dengan mudah sebagai kebalikan untuk y



V. untuk mengetahui formula ini, kita mungkin menggunakan aturan fuzzy IF-THEN:

Jika xBesar, maka y kecil (5.46) Dimana himpunan fuzzy “besar” dan “kecil” didefinisikan sebagai

Besar = 0/1 + 0,1/2 + 0,5/3 + 1/4 (5.47)

Jika kita menggunakan implikasi Dienes-Rescher (5.23), maka aturan fuzzy IF-THEN di interpretasikan mengikuti relasi fuzzy QD pada U



V :

QD = 1/(1, 1) + 1/(1, 2) + 1/(1, 3) + 1/(2, 1) + 0,9/(2, 2) + 0,9/(2, 3) + 1/(3, 1) +

0,5/(3, 2) + 0,5/(3, 3) + 1/(4, 1) + 0,5/(4, 2) + 0,1/(4, 3) (5.49)

Jika kita menggunakan implikasi Lukasiewicz (5.24), aturan (5.46) menjadi:

QL = 1/(1, 1) + 1/(1, 2) + 1/(1, 3) + 1/(2, 1) + 1/(2, 2) + 1/(2, 3) +1/(3, 1) + 1/(3, 2)

+ 0,6/(3, 3) + 1/(4, 1) + 0,5/(4, 2) + 0,1/(4, 3) (5.50)

Untuk implikasi Zadeh (5.25) dan implikasi Godel (5.46) kita mempunyai:

QZ = 1/(1, 1) + 1/(1, 2) + 1/(1, 3) + 0,9/(2, 1) + 0,9/(2, 2) + 0,9/(2, 3) + 0,5/(3, 1)

+ 0,5/(3, 2) + 0,5/(3, 3) + 1/(4, 1) + 0,5/(4, 2) + 0,1/(4, 3) (5.51)

dan

QG = 1/(1, 1) + 1/(1, 2) + 1/(1, 3) + 1/(2, 1) + 1/(2, 2) + 1/(2, 3) + 1/(3, 1) + 1/(3, 2)

+ 0,1/(3, 3) + 1/(4, 1) + 0,5/(4, 2) + 0,1/(4, 3) (5.52)

Akhirnya, Jika kita menggunakan implikasi Mamdani (5.31) dan (5.32), maka aturan fuzzy IF – THEN (5.46) menjadi:

QMM = 0/(1, 1) + 0/(1, 2) + 0/(1, 3) + 0,1/(2, 1) + 0,1/(2, 2) + 0,1/(2, 3) + 0,5/(3, 1)

+ 0,5/(3, 2) + 0,1/(3, 3) +1/(4, 1) + 0,5/(4, 2) + 0,1/(4, 3) (5.51)

dan

QMP = 0/(1, 1) + 0/(1, 2) + 0/(1, 3) + 0,1/(2, 1) + 0,05/(2, 2) + 0,01/(2, 3) + 0,5/(3,

1) +0,25/(3, 2) + 0,05/(3, 3) + 1/(4, 1) + 0,5/(4, 2) + 0,1/(4, 3) (5.52)

Untuk (5.49) – (5.52) kita melihat terdapat kombinasi tidak mencakup aturan (5.46) itu adalah, pasangan (1,1), (1,2), dan (1,3) (karena large (1) = 0 ) QD, QL, QZ, dan QG

keanggotaan nol. Ini konsisten dengan diskusi awal pada Implikasi global Dienes-Rescher, Lucasiewicz, Zadeh dan Godel, mengingat implikasi lokal Mamdani.

5.5 LATIHAN Latihan 5.1

Berikan tiga contoh variabel linguistik. Mengkombinasikan variabel linguistik menjadi proposisi majemuk fuzzy dan menentukan fungsi keanggotaannya.

Latihan 5.2

Pertimbangkan beberapa nilai linguistik hedges selain yang dalam Bagian 5.2 dan mengusulkan operasi yang wajar mewakili mereka.

Latihan 5.3

Biarkan QL, QG, QMM dan QMP menjadi hubungan fuzzy didefinisikan dalam (5.24),

(5.26), (5.31), dan (5.32), masing-masing. tunjukkan bahwa QMP



QMM



QG



QL

Latihan 5.4

Gunakan operator fuzzy dasar (3.1) - (3.3) untuk "tidak," "atau," dan "dan," masing-masing, dan menentukan fungsi keanggotaan untuk proposisi fuzzy (5.12) dan (5.13). potongan fungsi keanggotaan.

Latihan 5.5

Pertimbangkan aturan fuzzy IF-THEN (5.33) dengan fuzzy set lambat, kecil, dan besar didefinisikan oleh (5.42), (5.43) dan (5,44), masing-masing. menggunakan

min untuk t-norma di (5.16) dan menghitung hubungan fuzzy QD, QL, QZ, QG, QMM

dan QMP

Latihan 5.6

Misalkan Q hubungan fuzzy dalam U



U. Q disebut refleksif jika Q(u, u) = 1

(b) QQ o Q, di mana o menunjukkan komposisi max - min.

     



  





40 ; 0

40 30

; 10

40 1; 30

) (

x

x x x x