We emphasize here that while many crystals contain minor anisotropies in the Brillouin zone, the vast majority of crystals are thermally isotropic, with notable exceptions being materials with highly anisotropic bonds such as graphite. 3.5), the unknown distribution function is written as 3.4), we can get the equation for the temperature 4π∆eT. The integrals of the angles on the right-hand side of Eq. Therefore, a simple closed form of the temperature in Fourier space can be obtained. Note that if the spectral volumetric heat production Qω is a Dirac-delta function in time and space, equation 3.8) becomes the impulse temperature response or Green's function of the frequency-dependent BTE.
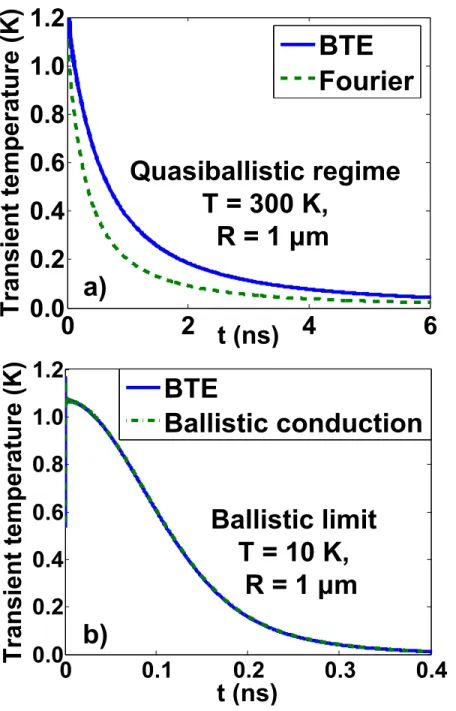
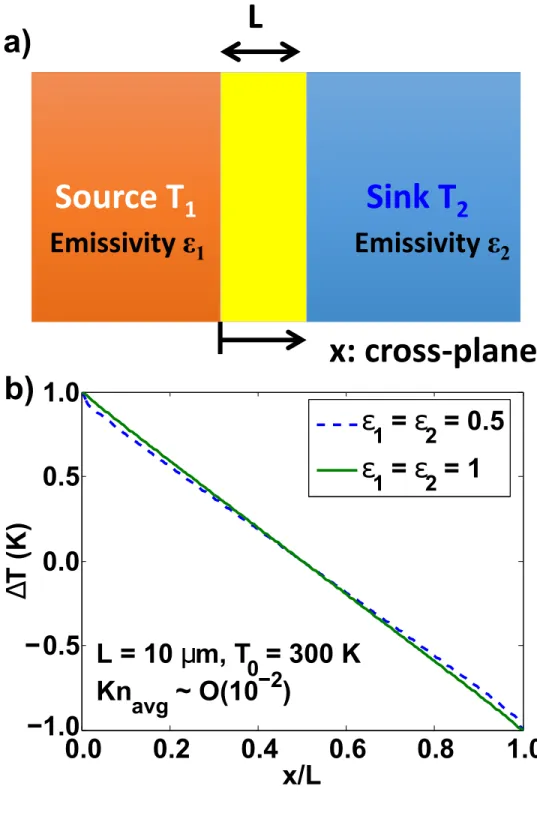
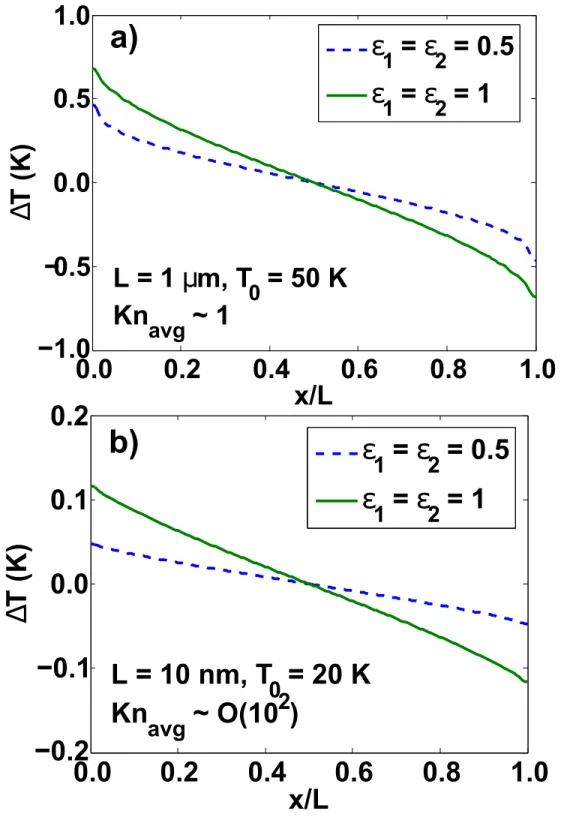
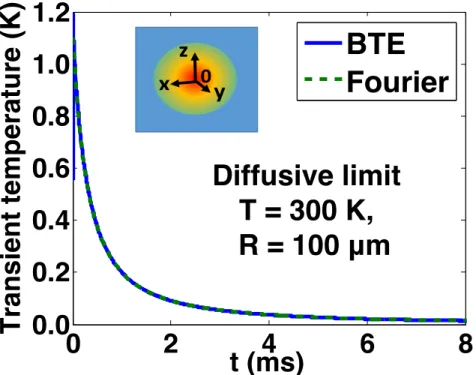
We next confirm that our solution reduces to the Green's function of the diffusive and ballistic regimes. As the Gaussian radius R decreases and MFPs become comparable to or larger than R , we observe a deviation of the BTE solution from Fourier's law due to quasi-ballistic transport, as shown in Fig. We note that the actual temperature rise is greater than the Fourier's. law prediction, consistent with a previous result by Chen.(40) The ballistic limit is shown in Fig.
3.2(b), demonstrating that the calculated temperature drop agrees with the ballistic BTE solution given by Eq. The sample surface undergoes periodic linear heating with width L in the x direction, exponential decay with penetration depth δ in the z direction, and time frequency η. By symmetry and uniqueness of the solution for the linear BTE, this solution is identical to the solution of the original problem.
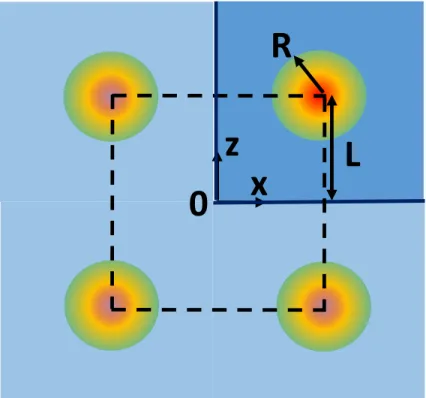
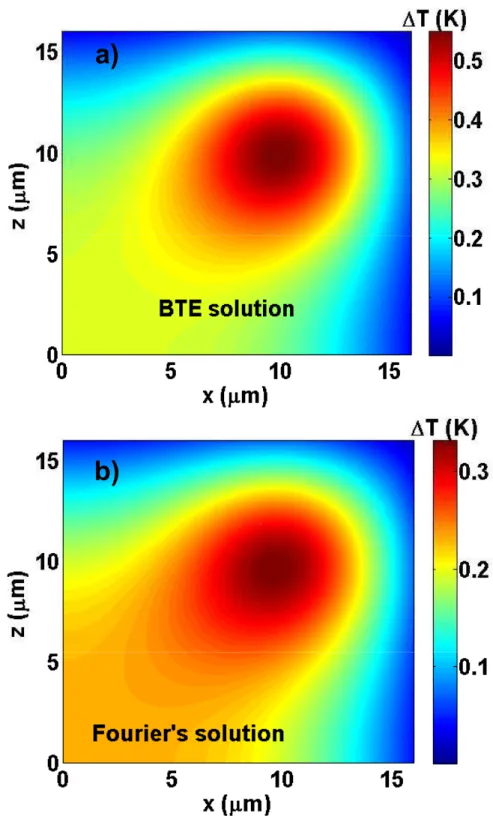
R2 , Read the offset distance from the center of hot toz/x-axis, and Draw the radius of the Gaussian profile. The radius of the Gaussian profile isRand the distance from the center of the heater to the x/zaxis is L. 3.5(a) & (b) give the amplitude of the temperature field when the heater is located 10 µm away from both x and z axes based on BTE respectively and Fourier's law.
For transport along the thin film, an analytical solution can be easily derived by assuming that the characteristic length scale of the thermal gradient is much longer than that of phonon MFPs. Here we present a semi-analytical solution of the frequency-dependent transient BTE using the method of degenerate kernels, also known as a series expansion method. (116) Our approach is valid from diffusive to ballistic transport regimes and is capable of a variety of boundary conditions, and is more than three orders of magnitude faster than previous numerical approaches. Considering the full phonon dispersion adds additional integrations to calculate each element of the matrix, dramatically increasing the computational cost.
This method is based on the expansion of all functions in Eq. 3.31) in a Fourier series, then solving for the coefficients of the temperature profile. Due to the symmetry of this domain, all the coefficients for the sine functions are equal to zero and the Fourier series for both functions reduces to a cosine expansion. Expressions for the elements in ¯¯A can be obtained analytically for the specific core here and are given in Appendix B for steady-state heat conduction with diffuse walls.
The elements in ¯¯A correspond to the Fourier coefficients of the kernel function K(bx,bx0), and ¯f is a vector of the Fourier coefficients of the inhomogeneous part of Eq.
Source T 1 Sink T 2
Emissivity ε 1 Emissivity ε 2a)
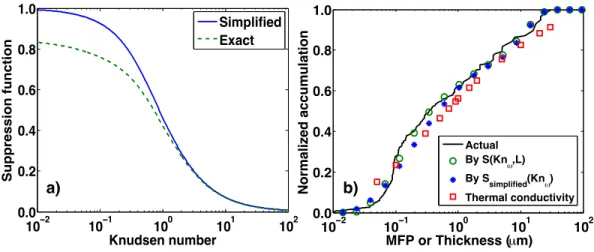
Our semi-analytical approach also allows us to obtain a simple closed-form expression for the in-plane thermal conductivity as a function of film thickness, analogous to the Fuchs-Sondheimer expression for in-plane thermal conductivity. With such a formula, the thermal conductivity over the entire plane can be easily evaluated, because the complete solution of the BTE is no longer necessary. The heat suppression function is defined as the ratio of the BTE to the Fourier heat flux(118), given as. 3.44).
Note that in general the suppression function does not only depend on Knω, but is also a function of the geometry through xm. This formula is analogous to the Fuch-Sondheimer equation for transport along thin films and allows the evaluation of the over-plane thermal conductivity, provided the expansion coefficients are known. A more useful result would be a suppression function that depends only on the Knudsen number, as is available for in-plane heat conduction with the Fuchs-Sondheimer formula (104,105).
This equation depends only on the Knudsen number and can therefore be used to directly evaluate the cross-plane thermal conductivity given the phonon distribution. 3.8(a) is that the exact and simplified suppression functions converge to the same curve at large Knω. Therefore, in the limit of very small distance between the boundaries, the only important part of the suppression function is at large values of Knudsen number exceeding Knω =1 because phonons possess a finite minimum MFP.
This simplification is very desirable because the simplified suppression function only depends on the Knudsen number and can therefore be applied without any knowledge of other material properties. Next, we apply this simplified suppression function to extract information about the phonon MPFs from the experimental measurements. In several works, thermal conductivity has been measured over variable lengths of nanostructures such as nanotubes, graphene ribbons and SiGe nanowires.
Xaxis corresponds to MFP for distributions and to plate thickness for thermal conductivity data. 3.46, we perform the above reconstruction procedure to recover the MFP spectrum from the thermal conductivity data as a function of plate thickness using accurate and simplified suppression functions. In the exact compression function case, each plate thickness has its own compression function given by Eq.
Although the smallest thickness we consider here is 50 nm, close to the ballistic regime, the simplified suppression function still gives a good prediction over the entire MFP spectrum, with a maximum deviation of 15% from the actual MFP spectrum. This result indicates that length-dependent thermal conductivity measurements, such as those recently reported for SiGe nanowires (119) and graphene ribbons (120) can be used to reconstruct the full MFP spectrum and not just an average MFP.