Buku Ajar Sistem Sensor 2022
Situs: eLDirU : eLearning of Jenderal Soedirman University Kelas: Arsip : Sistem Sensor A
Buku: Buku Ajar Sistem Sensor 2022
Dicetak Oleh: ABDULLAH NUR AZIZ
Tanggal: Wednesday, 15 February 2023, 05:58
Deskripsi
Pengukuran adalah aktivitas yang sangat penting dalam pengembangan sains dan teknologi. Mempelajari sistem pengukuran menjadi bagian yang tidak terpisahkan dalam kurikulum pembelajaran di perguruan tinggi.
Daftar isi
1. Karakteristik Statik 1.1. Capaian pembelajaran
1.2. Tujuan dan kinerja sistem pengukuran 1.3. Struktur sistem pengukuran
1.4. Karakteristik sistematik 1.5. Karakteristik statistik 1.6. Penentuan karakteristik statik
1.7. Model statik elemen sistem pengukuran 1.8. Ringkasan
1.9. Latihan
2. Akurasi Sistem dalam Kondisi Tunak 2.1. Capaian pembelajaran
2.2. Error sistem ideal 2.3. Error sistem non ideal 3. Karakteristik Dinamik 4. Efek Pembebanan 5. Sinyal dan Noise
6. Sensor dan Pengondisi Sinyal 7. Pemroses Sinyal
8. Presentasi Data
1. Karakteristik Statik
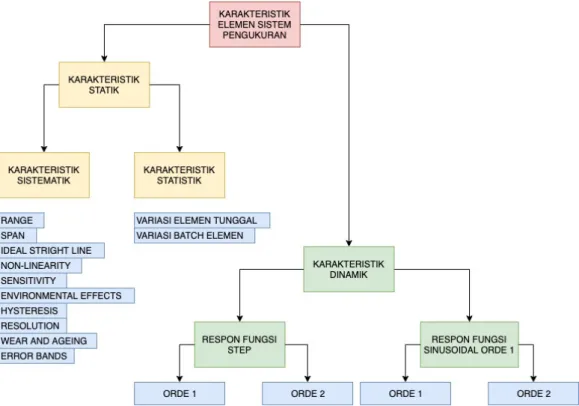
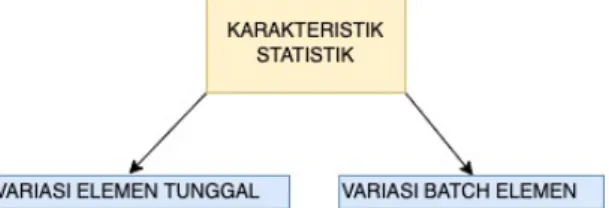
Bab ini akan membahas apa tujuan pembuatan sistem pengukuran dan bagaimana mengukur kinerja sebuah sistem pengukuran. Sistem pengukuran terdiri dari elemen-elemen sistem pengukuran. Setiap elemen memiliki karakteristik sendiri-sendiri. Karakteristik elemen sistem pengukuran ada dua yaitu statik dan dinamik. Karakteristik statik dari elemen sistem pengukuran meliputi karakteristik sistematik dan karakteristik statistik.
Gambar diagram skema karakteristik elemen sistem pengukuran
1.1. Capaian pembelajaran
Setelah mempelajari bab ini, mahasiswa akan dapat:
1. Mengenal elemen-elemen dalam sistem pengukuran;
2. Mengenal karakteristik sistematik dan statistik dari elemen sistem pengukuran;
3. Menentukan model elemen sistem pengukuran; dan
4. Menentukan karakteristik statik dan statistik elemen sistem pengukuran.
1.2. Tujuan dan kinerja sistem pengukuran
Sebelum membahas karakteristik statik elemen sistem pengukuran, terlebih dahulu dibahas tujuan dan kinerja sistem pengukuran.
Tujuan sistem pengukuran
Tujuan sistem pengukuran adalah sebagai jembatan antara proses dan pengamat. Proses adalah semua sistem yang bisa menghasilkan informasi seperti: reaktor kimia, pesawat, mobil, kapal, sistem cuaca, dan tubuh manusia. Pengamat adalah orang yang membutuhkan informasi yang dihasilkan dari proses-proses tadi. Ilustrasi tujuan sistem pengukuran dapat dilihat pada gambar berikut ini.
Gambar Tujuan sistem pengukuran
Kinerja sistem pengukuran
Gambar di atas menunjukkan bahwa pengamat tidak dapat mengakses informasi proses secara langsung melainkan harus melalui sistem pengukuran sebagai perantaranya. Oleh karena itu, informasi yang berasal langsung dari proses dinamakan True Value of Variable atau disingkat TV. Informasi ini menjadi input bagi sistem pengukuran untuk dikondisikan dan diproses hingga ditampilkan sebagai output ke hadapan pengamat. Pengamat memperoleh informasi tentang proses dari keluaran sistem pengukuran. Informasi tentang proses yang berasal dari sistem pengukuran dinamakan Measured Value of Variables atau disingkat MV.
Sistem pengukuran yang ideal menghasilkan MV yang sama dengan TV. Kinerja sistem pengukuran dinilai dari akurasinya. Akurasi adalah seberapa dekat nilai MV dengan TV. Karena sistem yang ideal hanya ada dalam teori, maka akurasi sistem pengukuran yang real dihitung melalui Error Sistem Pengukuran, E yang dihitung dengan formula:
atau
Contoh:
Kecepatan aliran fluida yang terukur (MV) adalah 11,0 m³/jam dan kecepatan aliran yang sebenarnya (TV) adalah 11,2 m³/jam. Tentukan Error sistem pengukuran!
Error sistem pengukuran adalah .■
𝐸 = 𝑀𝑉 − 𝑇𝑉
𝐸 = 𝚘𝚞𝚝𝚙𝚞𝚝 𝚜𝚒𝚜𝚝𝚎𝚖 −
𝚒𝚗𝚙𝚞𝚝 𝚜𝚒𝚜𝚝𝚎𝚖
𝐸 = 11, 0 − 11, 2 = −0, 2 𝑚
3/𝑗𝑎𝑚
1.3. Struktur sistem pengukuran
Sistem pengukuran minimal terdiri dari elemen-elemen sebagai berikut:
1. Elemen sensor;
2. Elemen pengondisi sinyal;
3. Elemen pemroses sinyal; dan 4. Elemen penampil data.
Hubungan antar elemen dapat dilihat pada gambar berikut:
Gambar hubungan antar elemen sistem pengukuran
Elemen sensor
Ini adalah elemen yang berhubungan langsung dengan proses yang sedang diukur. Elemen ini menghasilkan output yang berubah sesuai dengan perubahan pada input.
Contoh:
termokopel, menghasilkan emf (electromotive force / gaya gerak listrik) yang sebanding dengan temperatur;
strain gauge, di mana hambatannya tergantung pada regangan mekanik;
plat orifice, menghasilkan perbedaan tekanan yang nilainya tergantung kecepatan aliran fluida; dan sebagainya.
Elemen pengondisi sinyal
Elemen ini mengondisikan sinyal yang berasal dari elemen sensor dan merubahnya menjadi sinyal yang lebih sesuai untuk diproses lebih lanjut. Biasanya sinyal yang akan diproses lebih lanjut berbentuk arus dc (direct curent / arus searah) atau tegangan dc, atau sinyal frekuensi.
Contoh:
rangkaian jembatan, rangkaian ini mengubah perubahan impedansi menjadi perubahan tegangan;
penguat, bertugas menguatkan tegangan dari milivolt menjadi volt;
osilator, yang mengubah perubahan impedansi menjadi perubahan frekuensi; dan seterusnya.
Elemen pemroses sinyal
Elemen ini memroses output dari elemen pengondisi sinyal untuk diubah menjadi sinyal yang lebih sesuai untuk ditampilkan di elemen penampil.
Contoh:
Analog-to-Digital Converter (ADC), yang mengubah tegangan analog menjadi digital sehingga dapat diolah lebih lanjut di komputer;
Computer, yang mampu melakukan perhitungan atas sinyal-sinyal yang sudah direpresentasikan dalam bentuk digital; dan sebagainya.
Elemen penampil data
Elemen ini menampilkan informasi proses yang diukur dalam bentuk yang mudah dipahami oleh pengamat.
Contoh:
Indikator jarum Pencatat
Tampilan alpanumerik; dan Jenis penampil lainnya.
1.4. Karakteristik sistematik
Pada sub-bab sebelumnya kita melihat bahwa sistem pengukuran tersusun atas elemen-elemen sistem pengukuran. Sekarang kita akan meninjau karakteristik-karakteristik apa yang dimiliki oleh sebuah elemen dan apa pengaruh karakteristik tersebut terhadap kinerja keseluruhan dari sistem. Bagian pertama dari karakteristik statik elemen adalah karakteristik sistematik. Bagian kedua adalah karakteristik statistik.
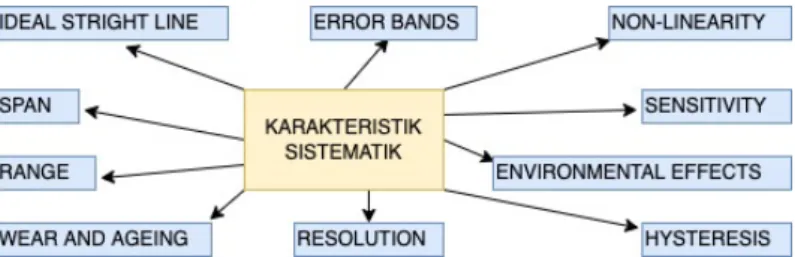
Gambar berikut menunjukkan karakteristik sistematik yaitu sifat elemen yang dapat dihitung langsung secara matematis maupun dari grafik.
Berbeda dengan karakteristik statistik, yaitu karakteristik yang tidak bisa ditentukan secara langsung.
Gambar lingkup karakteristik sistematik
Range
Range artinya adalah rentang yaitu nilai minimum dan maksimum dari input dan output elemen sistem pengukuran. Jadi range untuk input adalah sampai . Range untuk output adalah sampai .
Contoh:
sensor tekanan memiliki rentang input 0 - 10⁴ Pa dan rentang output 4 - 20 mA; dan termokopel memiliki rentang input 100 - 250ºC dan rentang output 4 - 10 mV.◼︎
Span
Span adalah variasi maksimum dari input dan output. Span input adalah dan span output adalah . Contoh:
sensor tekanan memiliki span input: 10⁴ Pa dan span output 16 mA; dan termokopel memiliki span input 150ºC dan span output 6 mV.◼︎
Ideal straight line
Elemen yang linier ditandai dengan titik-titik dalam koordinat kartesian dengan I berada di sumbu X dan O berada di sumbu Y di mana titik-titik tersebut membentuk garis lurus.
Ideal straight line nama lainnya adalah garis lurus ideal adalah garis yang menghubungkan titik dan . Persamaan garis lurus ideal adalah:
.
Setelah pindah ruas ke kanan, maka persamaan menjadi:
. Persamaan di atas adalah sama dengan:
, di mana
K adalah slope garis lurus ideal , dan
a adalah bias, yaitu titik potong garis dengan sumbu Y, . Contoh:
𝐼
𝑀𝐼𝑁𝐼
𝑀𝐴𝑋𝑂
𝑀𝐼𝑁𝑂
𝑀𝐴𝑋−
𝐼
𝑀𝐴𝑋𝐼
𝑀𝐼𝑁𝑂
𝑀𝐴𝑋− 𝑂
𝑀𝐼𝑁( , ) 𝑥
𝑖𝐼
𝑖𝑂
𝑖𝐴( 𝐼
𝑀𝐼𝑁, 𝑂
𝑀𝐼𝑁) 𝐵( 𝐼
𝑀𝐴𝑋, 𝑂
𝑀𝐴𝑋)
𝑂 − 𝑂
𝑀𝐼𝑁= [
𝑂𝐼𝑀𝐴𝑋𝑀𝐴𝑋−−𝑂𝐼𝑀𝐼𝑁𝑀𝐼𝑁] (𝐼 − 𝐼
𝑀𝐼𝑁)
𝑂
𝑀𝐼𝑁𝑂 = [
𝑂𝐼𝑀𝐴𝑋𝑀𝐴𝑋−−𝑂𝐼𝑀𝐼𝑁𝑀𝐼𝑁] (𝐼 − 𝐼
𝑀𝐼𝑁) + 𝑂
𝑀𝐼𝑁= 𝐾𝐼 + 𝑎 𝑂
𝐼𝐷𝐸𝐴𝐿=
𝑂𝐼𝑀𝐴𝑋𝑀𝐴𝑋−−𝑂𝐼𝑀𝐼𝑁𝑀𝐼𝑁= 𝑂
𝑀𝐼𝑁− 𝐾 𝐼
𝑀𝐼𝑁Sensor tekanan memiliki range input 0 - 10⁴ Pa dan range output 4 - 20 mA. Tentukan persamaan garis lurus ideal-nya!
Dari soal di atas diperoleh bahwa dan ; dan .
Sehingga slope garis dan titik potong dengan sumbu Y, .
Dengan demikian, persamaan garis lurus ideal sensor tekanan adalah . ◼︎
Non linearitas
Jika hubungan input - output elemen tidak memenuhi persamaan garis lurus ideal, maka elemen itu dinamakan elemen non linier. Non linieritas sebuah elemen didefinisikan oleh fungsi N(I) yang dihitung menggunakan persamaan berikut ini:
, atau .
Non linearitas sebuah elemen dapat juga diekspresikan dalam nilai non linearitas maksimumnya, yang dihitung sebagai percentage of full scale deflection (f.s.d) atau persentase-skala-simpangan-penuh sebagai berikut:
. Contoh:
Sebuah sensor tekanan mengeluarkan output yang beberapa di antaranya berbeda dengan garis lurus idealnya. Perbedaan terbesarnya adalah 2 mV. Jika span output adalah 100 mV, tentukan persentase max (f.s.d)-nya!
Perbedaan terbesar output sensor terhadap garis lurus ideal adalah , dan .
Sehingga persentase max (f.s.d) adalah sebesar:
.◼︎
Sensitivitas
Sensitivitas adalah perbandingan atas perubahan output, ΔO, setiap perubahan input sebesar ΔI. Dengan kata lain, sensitivitas adalah rasio . Jika ΔI sangat kecil mendekati nol, maka sensitivitas adalah turunan dO/dI dari garis lurus ideal. Untuk elemen yang linier, maka sensitivitasnya tidak lain adalah K atau slope garis lurus. Untuk elemen yang non linier, maka sensitivitasnya adalah . Contoh
Sebuah sensor memiliki karakteristik linier dengan persamaan garis lurus ideal: . Tentukan sensitivitas sensor tersebut!
Sensitivitas sensor adalah ◼︎
Environmental effects
Environmental effects adalah pengaruh lingkungan terhadap elemen sistem pengukuran. Contoh lingkungan adalah suhu sekitar, tekanan atmosfer, kelembaban relatif, tegangan catu daya, dan sebagainya. Lingkungan disimbolkan dengan L.
Lingkungan tempat di mana elemen berada bisa dikategorikan menjadi dua yaitu lingkungan standar dan tidak standar. Karakteristik statik garis lurus ideal (ideal straight line) dihitung dalam kondisi lingkungan standar. Dalam kondisi lingkungan tidak standar, maka K atau a dari persamaan garis lurus ideal bisa berubah, walaupun tidak selalu.
Jika pengaruh lingkungan mengubah sensitivitas, K, maka pengaruh tersebut dinamakan modifying input. Jika lingkungan mengubah titik potong dengan sumbu Y, a, maka pengaruh tersebut dinamakan interfering input.
Modifying input disimbolkan dengan I dan interfering input disimbolkan dengan I. Dalam kondisi lingkungan standar I = I= 0. Lingkungan standar disimbolkan dengan L . Nilai I dan I pada suatu pengukuran adalah selisih L saat itu dengan kondisi standar.
Contoh 1:
Sebuah elemen berada di suhu standar 20°C. Sensitivitas elemen pada kondisi standar adalah K. Sensitivitas elemen berubah pada suhu lingkungan 10°C dan 30°C. Tentukan modifying input pada suhu 10°C dan 20°C!
= 0 𝙿𝚊
𝐼
𝑀𝐼𝑁𝐼
𝑀𝐴𝑋= 10
4𝙿𝚊 𝑂
𝑀𝐼𝑁= 4 𝚖𝙰 𝑂
𝑀𝐴𝑋= 20 𝚖𝙰
𝐾 =
1020−44−0= 1, 6 × 10
−3𝑚𝐴𝑃𝑎𝑎 = 4 − (1, 6 × 10
−3× 0) = 4, 0 𝚖𝙰
= 1, 6 × 𝐼 + 4, 0 𝑂
𝐼𝐷𝐸𝐴𝐿10
−3𝑁(𝐼 ) = 𝑂(𝐼) − (𝐾𝐼 + 𝑎) 𝑂(𝐼) = 𝐾𝐼 + 𝑎 + 𝑁(𝐼)
𝑁 ̂ 𝙿𝚎𝚛𝚜𝚎𝚗𝚝𝚊𝚜𝚎 𝙼𝚊𝚡 (𝚏. 𝚜. 𝚍) =
𝙾𝙼𝙰𝚇𝙽̂−𝙾𝙼𝙸𝙽× 𝟷𝟶𝟶%
= 2 𝚖𝚅
𝑁 ̂ 𝑂
𝑀𝐴𝑋− 𝑂
𝑀𝐼𝑁= 𝚜𝚙𝚊𝚗 𝚘𝚞𝚝𝚙𝚞𝚝 = 𝟷𝟶𝟶 𝚖𝚅
𝙿𝚎𝚛𝚜𝚎𝚗𝚝𝚊𝚜𝚎 𝙼𝚊𝚡 (𝚏. 𝚜. 𝚍) =
𝟷𝟶𝟶𝟸× 𝟷𝟶𝟶% = 𝟸%
∆𝑂∆𝐼
= 𝐾 +
𝑑𝑂𝑑𝐼 𝑑𝑁 𝑑𝐼
𝑂 = 1, 6 × 10
−3𝐼 + 4, 0
= 1, 6 ×
𝑑𝑂𝑑𝐼
10
−3M I M I
0 M I
Suhu lingkungan standar adalah 20°C, maka L = 20°C.
Pada suhu lingkungan 10°C, maka L = 10°C dan I = L - L = -10°C.
Pada suhu lingkungan 30°C, maka L = 30°C dan I = L - L = 10°C.◼︎
Contoh 2:
Sebuah elemen berada di suhu standar 20°C. Bias elemen pada kondisi standar adalah a. Bias elemen berubah pada suhu lingkungan 10°C dan 30°C. Tentukan Interfering input pada suhu 10°C dan 20°C!
Suhu lingkungan standar adalah 20°C, maka L = 20°C.
Pada suhu lingkungan 10°C, maka L = 10°C dan I = L - L = -10°C.
Pada suhu lingkungan 30°C, maka L = 30°C dan I = L - L = 10°C.◼︎
Dengan berubahnya lingkungan, maka sensitivitas elemen bisa berubah. Jika sensitivitas berubah, maka sensitivitasnya sekarang menjadi K + K I . Demikian juga dengan bias, jika berubah karena pengaruh lingkungan, maka biasnya sekarang menjadi a + K I. K laju perubahan sensitivitas terhadap perubahan lingkungan dan K adalah laju perubahan bias terhadap perubahan lingkungan.
Contoh 3:
Sebuah elemen berada di suhu standar 20°C. Sensitivitas elemen pada kondisi standar adalah K. Sensitivitas elemen berubah pada suhu lingkungan 10°C dan 30°C. Tentukan sensitivitas elemen pada suhu 10°C dan 20°C!
Modifying input pada suhu 10°C, I = -10°C, maka sensitivitas = K - 10K .◼︎
Modifying input pada suhu 10°C, I = 10°C, maka sensitivitas = K + 10K .◼︎
Contoh 4:
Sebuah elemen berada di suhu standar 20°C. Bias elemen pada kondisi standar adalah a. Bias elemen berubah pada suhu lingkungan 10°C dan 30°C. Tentukan bias elemen pada suhu 10°C dan 20°C!
Interfering input pada suhu 10°C, I = -10°C, maka sensitivitas = K - 10K .◼︎
Interfering input pada suhu 10°C, I = 10°C, maka sensitivitas = K + 10K .◼︎
Dengan memperhitungkan pengaruh lingkungan, maka persamaan garis dari elemen sistem pengukuran menjadi:
, atau dalam bentuk lain .
Hysteresis
Untuk input yang sama, I, kadang output sebuah elemen, O, dapat berbeda tergantung apakah I-nya naik atau I-nya turun. Histerisis adalah perbedaan dari kedua macam O tadi. Jadi histerisis adalah semua nilai selisih O untuk setiap I saat naik dan I saat turun, atau:
Histerisis sebuah elemen juga bisa dinyatakan dalam histerisis maksimum dalam persentase simpangan penuh. Jika histerisis maksimum dinyatakan dengan , maka:
. Contoh:
Sebuah sensor tinggi permukaan air (level) memiliki rentang input 0 - 15 cm. Setelah dikalibrasi diperoleh hasil sebagai berikut:
Tabel kalibrasi sensor level
Level, h (cm) 0,0 1,5 3,0 4,5 6,0 7,5 9,0 10,5 12,0 13,5 15,0 Output (volts) saat h naik 0,00 0.35 1.42 2.40 3.43 4.35 5.61 6.50 7.77 8.85 10.02 Output (volts) saat h turun0.14 1.25 2.32 3.55 4.43 5.70 6.78 7.8 8.87 9.65 10.2 Tentukan histerisis maksimum dalam persentase f.s.d!
0
M 0
M 0
0
I 0
I 0
M M I I M
I
M M
M M
i I
i I
𝑂(𝐼) = 𝐾𝐼 + 𝑎 + 𝑁(𝐼) + 𝐾
𝑀𝐼
𝑀𝐼 + 𝐾
𝐼𝐼
𝐼𝑂(𝐼) = (𝐾 + 𝐾
𝑀𝐼
𝑀)𝐼 + 𝑎 + 𝐾
𝐼𝐼
𝐼+ 𝑁(𝐼)
𝐻(𝐼) = 𝑂(𝐼 )
↓− 𝑂(𝐼 )
↑𝐻 ̂
𝙷𝚒𝚜𝚝𝚎𝚛𝚒𝚜𝚒𝚜 𝚖𝚊𝚔𝚜𝚒𝚖𝚞𝚖 𝚜𝚎𝚋𝚊𝚐𝚊𝚒 𝚙𝚎𝚛𝚜𝚎𝚗𝚝𝚊𝚜𝚒 𝚏. 𝚜. 𝚍 =
𝙾𝙼𝙰𝚇−𝙷̂𝙾𝙼𝙸𝙽× 𝟷𝟶𝟶%
Dari tabel kalibrasi diperoleh:
Sehingga .
Karena , maka
.◼︎
Resolusi
Resolusi adalah perubahan input ΔI terbesar yang belum membuat output O berubah. Resolusi diekspresikan sebagai ΔI terbesar dalam persentase full scale display (f.s.d) yaitu:
. Contoh:
Sebuah potensiometer geser terbuat dari 100 lilitan kawat. Tentukan resolusinya dalam persentase f.s.d!
Karena ada 100 lilitan, maka hambatan tidak akan berubah sebelum bergeser dari satu lilitan ke lilitan berikutnya. Sehingga resolusinya adalah:
◼︎
Wear and ageing
Wear and ageing adalah penggunaan dan usia. Artinya, karena digunakan dan karena usia maka elemen sistem pengukuran bisa mengalami perubahan pada K dan a. Misal konstanta pegas pada sebuah per (k) akan berkurang seiring bertambahnya umur pegas maupun seiring penggunaannya, sebagaimana diilustrasikan pada persamaan berikut:
;
di mana k adalah konstanta pegas mula-mula, b adalah konstanta dan t adalah waktu.
Error band
Karakteristik sistematik (non-linieritas, histeresis, dan resolusi) pada sensor modern nilainya sangat kecil sehingga jadi tidak realistis jika dihitung satu persatu. Sebagai gantinya, pabrik pembuat sensor memberikan error band (pita error) sebagai karakteristik sensornya.
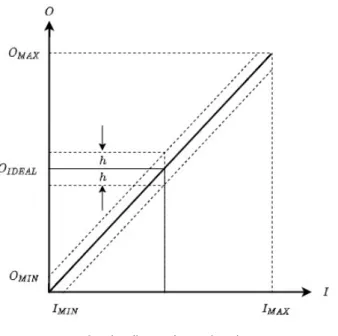
Arti pita error adalah bahwa untuk setiap input I, elemen akan menghasilkan output O yang nilainya berada diantara dua garis ±h yang melintang sejajar dengan garis O . Ilustrasi pita error dalam kurva garis lurus ideal adalah sebagai berikut:
Gambar ilustrasi error band
Gambar ilustrasi di atas menunjukkan bahwa untuk setiap input I, maka peluang bahwa outputnya ada di antara O - h dan O + h adalah = 1, atau dengan kata lain output, O, pasti berada di antara kedua nilai itu.
𝑂(𝐼 )
↓− 𝑂(𝐼 )
↑= 0, 14; 0, 9; 0, 9; 1, 15; 1, 0; 1, 35; 1, 17; 1, 3; 1, 1; 0, 8; 0, 18
= 1, 35 𝐻 ̂
− = 10, 2 − 0 = 10, 2 𝚅𝚘𝚕𝚝𝚜 𝑂
𝑀𝐴𝑋𝑂
𝑀𝐼𝑁𝙷𝚒𝚜𝚝𝚎𝚛𝚒𝚜𝚒𝚜 𝚖𝚊𝚔𝚜𝚒𝚖𝚞𝚖 𝚜𝚎𝚋𝚊𝚐𝚊𝚒 𝚙𝚎𝚛𝚜𝚎𝚗𝚝𝚊𝚜𝚒 𝚏. 𝚜. 𝚍 =
𝟷,𝟹𝟻𝟷𝟶,𝟸× 𝟷𝟶𝟶% = 𝟷𝟹, 𝟸𝟺%
× 100%
Δ𝐼𝑅
− 𝐼𝑀𝐴𝑋 𝐼𝑀𝐼𝑁
× 100% = 1%
1001
t
𝑘(𝑡) = 𝑘
0− 𝑏𝑡
0
IDEAL
IDEAL IDEAL
1.5. Karakteristik statistik
Karakteristik statistik diperoleh melalui pengukuran berulang pada sebuah elemen atau melalui pengukuran terhadap seluruh elemen yang diproduksi dalam satu kelompok. Oleh karena itu, kita membagi pembahasan kali ini ke dalam dua bagian, seperti pada gambar berikut.
Pertama adalah variasi statistik pada output dari elemen tunggal terhadap waktu. Kedua adalah variasi statistik pada sekelompok elemen yang sejenis.
Gambar lingkup karakteristik statistik
Variasi statistik pada output elemen tunggal
Bayangkan sebuah sensor tekanan yang menerima input konstan sebesar 0,5 bar selama beberapa hari. Dengan input tersebut, diharapkan output sensor adalah sebesar 1,0 volt. Namun output sensor ternyata tidak konstan menunjukkan angka sebesar 1,0 volt setiap saat, melainkan bervariasi seperti 0,99; 1,01; 1,00; 1,02; 0,98; dst. Variasi tersebut berada di sekitar angka yang diharapkan yaitu 1,0 volt. Kejadian tersebut mencerminkan kurangnya repeatability elemen sistem pengukuran. Repeatability adalah kemampuan elemen menghasilkan output yang sama terus menerus jika menerima input yang sama.
Kurangnya repeatability disebabkan oleh pengaruh proses random pada elemen dan lingkungan. Biasanya yang menjadi penyebab adalah fluktuasi acak pada I dan I. Dengan mengasumsikan probability density function pada input-input I, I , dan I secara tepat, maka kita dapat menentukan probability density function dari output.
:::::::::::::::::::::::::::::::::::::::::::::::::::
Probability density function
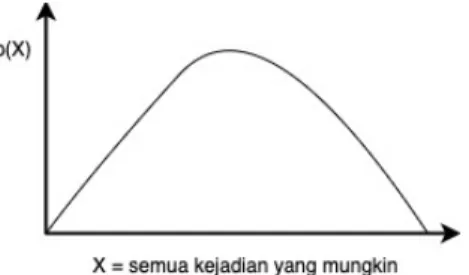
Probability density function (pdf) adalah suatu fungsi yang menyatakan nilai probabilitas dari setiap kejadian X dan dituliskan sebagai p(x).
Karena menyatakan probabilitas, maka 0 ≤ P(X) ≤ 1. Jumlah semua kemungkinan adalah sama dengan satu, atau . Grafik pdf menyatakan nilai kemungkinan dari setiap kejadian. Sumbu x menyatakan kejadian yang mungkin, dan sumbu y menyatakan nilai kemungkinannya, p(x) sebagaimana diilustrasikan oleh gambar di bawah ini.
Gambar ilustrasi probability density function
Mengapa pdf dari data menjadi penting? Karena dengan pdf, kita dapat mengetahui apakah kesimpulan-kesimpulan yang diambil dalam perhitungan statistik menunjukkan keadaan yang sebenarnya atau tidak?
Salah satu pdf yang sering digunakan adalah Gaussian. Pdf ini memiliki bentuk persamaan sebagai berikut:
dalam persamaan di atas:
adalah rata-rata, atau yang diharapkan muncul (nilai ini menentukan titik tengah distribusi); dan adalah simpangan baku (nilai ini menentukan distribusi sebaran).
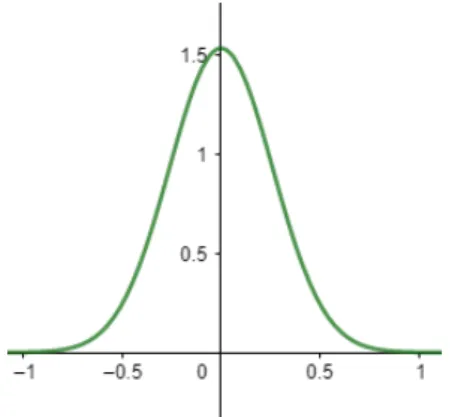
Kurva pdf Gaussian kurang lebih dapat dilihat pada gambar berikut ini.
M I M I
𝑝(𝑥 = ) = 1
∑
𝑛𝑥
𝑛 i𝑝(𝑥) =
𝜎√12𝜋𝑒𝑥𝑝
(−
)(𝑥−𝑥¯)2 2𝜎2
𝑥 ¯
𝜎
Gambar pdf Gaussian dengan dan Dengan dan , maka pdf gambar di atas adalah:
.
:::::::::::::::::::::::::::::::::::::::::::::::::::
Mari kita tulis ulang persamaan pada sub bab 1.4 yaitu output elemen sistem pengukuran yang melibatkan non-linieritas dan pengaruh lingkungan:
,
Persamaan tersebut menggambarkan hubungan variabel dependen O dengan variabel independen I, I , dan I. Akibatnya, jika perubahan kecil pada O di sekitar rerata O, selanjutnya disebut ΔO, disebabkan oleh perubahan kecil ΔI, ΔI , dan ΔIdi sekitar nilai rerata I, I , dan I , maka ΔO dapat dihitung sebagai berikut:
.
Persamaan di atas menyatakan ΔO adalah kombinasi linier dari ΔI, ΔI , dan ΔI. Jika kombinasi linier, maka berlaku bahwa simpangan baku dari ΔO, atau output di sekitar O adalah:
. dengan
adalah deviasi standar input. Namun demikian, juga dapat dihitung langsung dari pengukuran berulang terhadap output elemen.
Rerata output elemen dapat dihitung menggunakan persamaan:
.
Adapun bentuk fungsi pdf dari semua kemungkinan output elemen adalah .
Variasi statistik pada elemen berkelompok
Mari kita lihat dua informasi yang mungkin terjadi berikut ini.
Yang pertama, misal kita membeli 100 buah sensor suhu RTD dengan nilai hambatan 100Ω. Kemudian kita mengukur hambatan semua sensor. Setelah diukur, ternyata nilai hambatannya bervariasi, ada yang di atas 100Ω, ada juga yang di bawah 100Ω. Namun rata-rata di sekitar nilai 100Ω, misal 100,1 Ω dan simpangan baku 0,1Ω. Hal ini disebabkan oleh variasi acak yang terjadi pada saat pembuatan komponen sensor.
Yang kedua, sementara itu dari data spesifikasi RTD yang dikeluarkan oleh pemanufaktur, disebutkan bahwa pabrik hanya memberi toleransi sebesar ±0,15Ω pada komponen yang mereka jual. Artinya, untuk R = 100,0 Ω, dengan toleransi ±0,15Ω, maka pabrik akan membuang semua RTD yang memiliki R < 99,85Ω dan R > 100,15Ω.
Dari dua informasi di atas, kita memiliki dua pilihan:
1. Tetap menggunakan RTD yang sudah dibeli dan percaya dengan informasi yang diberikan oleh pemanufaktur bahwa hambatan
𝑥 ¯ = 0 𝜎 = 0, 26
= 0
𝑥 ¯ 𝜎 = 0, 26 𝑝(𝑥) =
√2𝜋 . 0,261 2𝑒𝑥𝑝
(−
)𝑥2 2 . 0,262
𝑂(𝐼) = (𝐾 + 𝐾
𝑀𝐼
𝑀)𝐼 + 𝑎 + 𝐾
𝐼𝐼
𝐼+ 𝑁(𝐼)
M I
M I M I
Δ𝑂 =
( )𝛿𝑂𝛿𝐼Δ𝐼 + ( )
𝛿𝑂Δ + ( ) Δ
𝛿𝐼𝑀
𝐼
𝑀 𝛿𝑂 𝛿𝐼𝐼𝐼
𝐼M I
=
𝜎
𝑂 ( )𝛿𝑂𝛿𝐼 2𝜎
𝐼2+ ( )
𝛿𝐼𝛿𝑂𝑀+
2
𝜎
𝐼2𝑀( )
𝛿𝐼𝛿𝑂𝐼2
𝜎
𝐼2𝐼‾ ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ ‾
√
, ,
𝜎
𝐼𝜎
𝐼𝑀𝜎
𝐼𝐼𝜎
𝑂= 𝐾 + 𝑎 + 𝑁( ) + + 𝑂 ¯ 𝐼 ¯ 𝐼 ¯ 𝐾
𝑀𝐼
𝑀¯ 𝐼 ¯ 𝐾
𝐼𝐼 ¯
𝐼𝑝(𝑂) =
𝜎𝑂√12𝜋𝑒𝑥𝑝
(−
)(𝑂−𝑂¯)2 2𝜎𝑂2
0
komponen R = 100,0 Ω. Kita tidak mempermasalahkan hasil pengukuran terhadap 100 komponen yang menunjukkan nilai reratanya adalah 100,1 Ω. Pilihan ini yang paling mudah.
2. Kita melakukan kalibrasi dengan teliti terhadap setiap komponen yang dibeli sehingga diperoleh R yang akurat. Pilihan ini memakan waktu lama dan mahal. Selain itu, adanya keterbatasan akurasi pada peralatan kalibrasi juga berpengaruh pada munculnya ketidak pastian pada R .
Dalam setiap kumpulan sensor identik yang dibuat pada seri yang berbeda, kita tetap akan menjumpai adanya variasi pada masing-masing komponen. Secara umum dapat dikatakan, bahwa nilai-nilai parameter sensor seperti K dan a akan terdistribusi secara statistik di sekitar dan .
Jadi dalam kasus di mana terdapat kumpulan komponen identik yang dibuat pada seri yang berbeda, maka variasi output komponen bisa disebabkan oleh variasi lingkungan dalam bentuk input I, I , dan I, dan juga bisa disebabkan oleh variasi parameter K dan a dari komponen.
Jika kurva distribusi dari variasi lingkungan pada input komponen dan variasi parameter pada komponen diasumsikan berbentuk normal, maka kurva distribusi dari output juga berbentuk normal. Artinya probabilitas setiap nilai output berada di dalam kurva distribusi normal yang ditunjukkan oleh persamaan:
, di mana:
rerata adalah
; dan dan 𝝈 dihitung dengan persamaan:
. Contoh:
Tinjaulah sebuah sensor suhu berupa termokopel berikut ini:
Gambar diagram input dan output sensor termokopel Output termokopel dihitung dengan persamaan sebagai berikut:
pada suhu (50 - 150ºC).
Rata-rata dari parameter adalah sbb:
; dan Deviasi standar dari parameter adalah sbb:
.
Tentukan rata-rata output sensor dan deviasi standarnya, jika input sensor adalah 110ºC.
Rata-rata output sensor:
◼︎
Deviasi standar output sensor:
∂E/∂a = 1; ∂E/∂T = -4,026 x 10 . ∂E/∂a dan ∂E/∂a tidak dihitung karena 𝝈 dan 𝝈 = 0.
◼︎
0
0
0
𝐾 ¯ 𝑎 ¯
M I
𝑝(𝑂) =
𝜎𝑂√12𝜋𝑒𝑥𝑝
(−
)(𝑂−𝑂¯)2 2𝜎𝑂2
𝑂 ¯
= + + 𝑁( ) + + 𝑂 ¯ 𝐾 ¯ 𝐼 ¯ 𝑎 ¯ 𝐼 ¯ 𝐾 ¯
𝑀𝐼
𝑀¯ 𝐼 ¯ 𝐾 ¯
𝐼𝐼 ¯
𝐼o
𝜎
𝑂=
( )𝛿𝑂𝛿𝐼 2𝜎
𝐼2+ ( )
𝛿𝐼𝛿𝑂𝑀+ + + + …
2
𝜎
𝐼2𝑀( )
𝛿𝐼𝛿𝑂𝐼2
𝜎
𝐼2𝐼 ( )𝛿𝑂𝛿𝐾 2𝜎
𝐾2 ( )𝛿𝑂𝛿𝑎 2𝜎
2𝑎‾ ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ ‾
√
= + (𝑇 − ) + ( − )
𝐸
𝑇,𝑇𝑎𝑎
0𝑎
1𝑇
𝑎𝑎
2𝑇
2𝑇
𝑎2= 0, 00; = 4, 017 × ; = 4, 66 × ; = 10 𝑎 ¯
0𝑎 ¯
110
2𝑎 ¯
210
−6𝑇 ¯
𝑎= 6, 93 × ; = 0, 0; = 0, 0; = 6, 7 𝜎
𝑎010
−2𝜎
𝑎1𝜎
𝑎2𝜎
𝑇𝑎= 0, 0 + 4, 017 × 2(110 − 10) + 4, 66 × ( − ) = 4, 07 𝚖𝚅
𝐸
110,1010
−10
−6110
210
20 a -2
1 2 a1 a2
=
𝜎
𝐸( )
𝛿𝑎𝛿𝐸0+
2
𝛿
2𝑎0( )
𝛿𝑇𝛿𝐸𝑎2
𝛿
2𝑇𝑎‾ ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ ‾
√
= = 0, 28 𝚖𝚅
𝜎
𝐸√ 1, ‾ ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ 0
2× (6, 93 × 10
−2)
2+ (−4, 026 × 10
−2)
2× 6, 7 ‾
21.6. Penentuan karakteristik statik
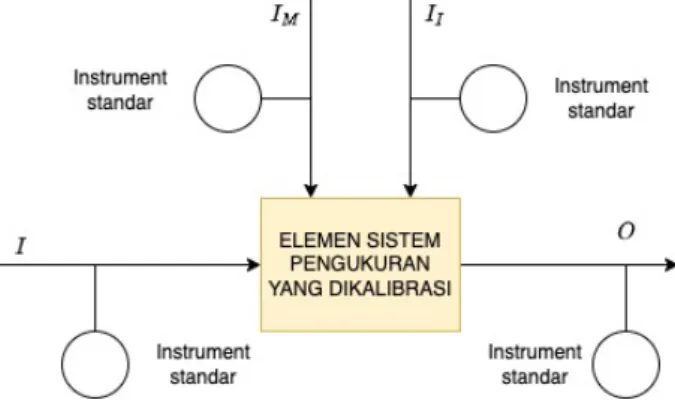
Penentuan karakteristik statik dilakukan melalui proses kalibrasi. Kalibrasi adalah proses pengukuran input I, output O, maupun input lingkungan I dan I, baik I dalam kondisi konstan atau kondisi berubah perlahan-lahan. Peralatan dan metode yang digunakan untuk mengukur variabel-variabel tadi dinamakan standar. Ilustrasi proses kalibrasi menggunakan standar dapat dilihat pada gambar berikut.
Gambar skema kalibrasi elemen sistem pengukuran
Akurasi dalam pengukuran suatu besaran adalah seberapa dekat measurement value (MV) dengan true value (TV). Secara kuantitatif, akurasi tidak lain adalah kesalahan pengukuran yang dihitung dari pengurangan MV atas TA atau E = MV - TV.
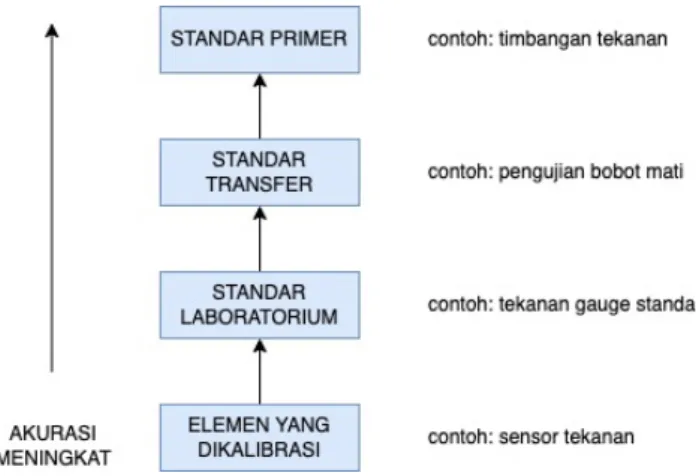
TV adalah nilai pengukuran pada suatu standar dengan akurasi sangat baik. Standar memiliki tingkatan-tingkatan. Tingkatan standar dari yang akurasinya paling tinggi ke yang paling rendah adalah: standar primer, standar transfer, dan standar laboratorium. Sehingga kalibrasi dapat dilaksanakan secara bertingkat, yaitu elemen sistem pengukuran dikalibrasi menggunakan standar di laboratorium, standar di laboratorium dikalibrasi menggunakan standar transfer, dan standar transfer dikalibrasi menggunakan standar primer. Tahap-tahap ini membentuk tangga keterlacakan seperti pada gambar berikut.
Gambar skema tangga keterlacakan (traceability ladder)
Satuan SI
The International Systems of Units (SI) adalah sistem satuan yang dibangun berdasarkan besaran-besaran dasar. Besaran-besaran dasar berikut ini, masing-masing memiliki standar yang berbeda-beda. Besaran dasar adalah besaran-besaran yang diyakini tidak terkait satu sama lain.
Besaran turunan adalah besaran selain besaran dasar yang didefinisikan menggunakan besaran-besaran dasar melalui persamaan kuantitatif.
Penjelasan mengenai satuan SI dapat dilihat di sini.
Penggunaan satuan SI di Indonesia salah satunya terdapat dalam UU no 2 tahun 1981 tentang Metrologi Legal.
Lingkup kegiatan kalibrasi
Lingkup kegiatan kalibrasi dibagi menjadi tiga bagian utama.
O versus I dengan I = I = 0
M I
M I
Pada bagian ini, langkah-langkah yang dilakukan adalah seperti pada gambar berikut:
Gambar skema langkah kalibrasi O vs I 1. Memastikan dilakukan di lingkungan standar, atau I = I = 0;
2. Beri input I dengan meningkat secara bertahap dengan interval 10% dari I sampai I ;
3. Pada setiap interval, sediakan waktu secukupnya sampai sistem stabil sebelum pembacaan data pengukuran dilakukan;
4. Beri input I secara bertahap mulai dari I sampai ke I dengan interval 10% dalam setiap tahapnya;
5. Ulanglah seluruh proses "naik" dan "turun" sebanyak dua set lagi;
6. Tentukan parameter a ... a dari polinomial dengan cara meminimalkan persamaan kriteria , di mana
! Prosedur minimalisasinya bisa menggunakan metode polinomial fiting dengan bantuan google sheet atau excel.
7. Tentukan histeresis, H(I) dengan cara memisahkan data-data naik dan data turun ;
1. Tentukan parameter dari polinomial dan dengan metode polinomial fitting;
2. Histeresis dikatakan nyata (signifikan) jika jarak antara kedua kurva lebih besar daripada jarak antar titik data;
3. Jika histeresis nyata, maka hitunglah histeresis dengan persamaan ;
4. Jika histeresis tidak nyata, maka bisa diabaikan dan data bisa dikombinasikan menjadi satu untuk menentukan ; 8. Tentukan K dan a menggunakan data dan untuk menyusun persamaan garis lurus ideal ; dan 9. Tentukan nonlinieritas N(I) = O(I)-(KI + a).
O versus I , I saat I konstan
Langkah-langkah pada bagian ini dapat dilihat pada gambar berikut:
M I
MIN MAX
MAX MIN
0 m
𝑂(𝐼) = ∑
𝑞=𝑚𝑞=0𝑎
𝑞𝐼
𝑞𝑦 = ∑
𝑖=𝑚𝑖=1𝑑
2𝑖= 𝑂( ) − 𝑑
𝑖𝐼
𝑖𝑂
𝑖( , 𝐼
𝑖𝑂
𝑖)
𝐼↑( , 𝐼
𝑗𝑂
𝑗)
𝐼↓𝑂(𝐼 )
𝐼↑= ∑
𝑞=𝑚𝑞=0𝑎
↑𝑞𝐼
𝑞𝑂(𝐼 )
𝐼↓= ∑
𝑞=𝑚𝑞=0𝑎
↓𝑞𝐼
𝑞𝐻(𝐼) = 𝑂(𝐼 )
↓− 𝑂(𝐼 )
↑( 𝐼
𝑀𝐼𝑁, 𝑂
𝑀𝐼𝑁) ( 𝐼
𝑀𝐴𝑋, 𝑂
𝑀𝐴𝑋) 𝑂(𝐼)
M I
Gambar skema langkah kalibrasi faktor lingkungan 1. Tentukan faktor lingkungan yang menjadi interfering input, Idengan cara:
1. Input I diset di I ;
2. Ubahlah lingkungan yang diduga sebagai interfering input, dan input yang lain tetap. Kemudian ukurlah ada tidaknya ΔO pada output. Jika ada, maka faktor lingkungan tersebut berperan sebagai interfering input, I. Jika tidak ada perubahan output, atau ΔO=0, berarti faktor lingkungan tersebut bukan sebagai interfering input;
3. Jika ada interfering input, maka hitunglah ; dan
4. Lakukan 1 - 4 untuk semua kemungkinan interfering input yang teridentifikasi.
2. Tentukan faktor lingkungan yang menjadi modifying input, I dengan cara:
1. Input I diset di tengah-tengah antara I dan I yaitu ½(I + I );
2. Ubahlah lingkungan yang diduga sebagai modifying input, dan input lain dibuat tetap. Kemudian ukurlah ada tidaknya ΔO pada
I MIN
I
= Δ𝑂/Δ 𝐾
𝐼𝐼
𝐼M
MIN MAX MIN MAX
output. Jika ada, maka faktor lingkungan tesebut berperan sebagai modifying input, I . Jika tidak ada perubahan output, atau ΔO=0, berarti faktor lingkungan tersebut bukan modifying input;
3. Jika ada modifying input dan ini tidak teridentifikasi sebagai interfering input, maka hitunglah ; 4. Jika ternyata modifying input juga teridentifikasi sebagai interfering input dan memiliki K pada langkah sebelumnya, maka
hitunglah: .
Repeatability test
Langkah-langkah dalam repeatability test adalah sebagai berikut:
Gambar skema repeatability test
1. Ujilah elemen pengukuran di lingkungan kerja aslinya, sehingga elemen tersebut mengalami variasi random dari lingkungan I dan I; 2. Input I diset dipertahankan di tengah-tengah antara I dan I selama beberapa hari;
3. Output O diukur sehingga dihasilkan sejumlah nilai O, k = 1, 2, ..., N;
4. Hitung rata-rata O dengan ;
5. Hitung deviasi standar dengan ;
6. Buat histogram dari O;
7. Bandingkan dengan kurva distribusi normal yang diperoleh dari pdf dengan parameter dan ; Contoh:
Test repeatability dilakukan terhadap sensor tekanan dan diperoleh 50 buah data output yang berada di antara 0,975 dan 1,030 V.
Kelimapuluh data output tadi dikelompokkan dalam 11 interval, masing-masing sebesar 0,005 V. Frekuensi output di tiap interval adalah sebagai berikut:
0,975 - 0,979 V = 1 buah;
M
= =
𝐾
𝑀 1 𝐼 Δ𝑂Δ𝐼𝑀
+2 𝐼𝑀𝐼𝑁 𝐼𝑀𝐴𝑋
Δ𝐼Δ𝑂𝑀
I
=
[−
]𝐾
𝑀 2+ 𝐼𝑀𝐼𝑁 𝐼𝑀𝐴𝑋
Δ𝐼Δ𝑂𝐼,𝑀
𝐾
𝐼M I
MIN MAX
k
=
𝑂 ¯
𝑁1∑
𝑘=𝑁𝑘=𝑖𝑂
𝑘=
𝜎
0 √‾
𝑁1‾‾‾‾‾‾‾‾‾‾‾‾‾‾ Σ
𝑁𝑘=1( 𝑂
𝑘− 𝑂 ¯)
2‾
k
𝑂 ¯ 𝜎
𝑜(𝑁 = 50)
0,980 - 0,984 V = 3 buah;
0,985 - 0,989 V = 2 buah;
0,990 - 0,994 V = 7 buah;
0,995 - 0,999 V = 12 buah;
1,000 - 1,004 V = 10 buah;
1,005 - 1,009 V = 8 buah;
1,010 - 1,014 V = 3 buah;
1,015 - 1,019 V =1 buah;
1,020 - 1,024 V = 2 buah;
1,025 - 1,029 V = 1 buah;
1. Tentukan peluang dan density probability dari output sensor tekanan pada repeatability test di atas!
2. gambarlah histogram density probabilitynya!
3. tentukan rata-rata dan standar deviasi!
4. gambarlah pdf-nya!
Jawab:
Dengan jumlah data output N = 50, maka peluang dari tiap interval dihitung dengan rumus , 0,975 - 0,979 V = 1 buah; peluang = 1/50 = 0,02;
0,980 - 0,984 V = 3 buah; peluang = 3/50 = 0,06;
0,985 - 0,989 V = 2 buah; peluang = 0,04;
0,990 - 0,994 V = 7 buah; peluang = 0,14;
0,995 - 0,999 V = 12 buah; peluang = 0,24;
1,000 - 1,004 V = 10 buah; peluang = 0,2;
1,005 - 1,009 V = 8 buah; peluang = 0,16;
1,010 - 1,014 V = 3 buah; peluang = 0,06;
1,015 - 1,019 V =1 buah; peluang = 0,02;
1,020 - 1,024 V = 2 buah; peluang = 0,04;
1,025 - 1,029 V = 1 buah; peluang = 0,02;
Adapun kepadatan probabilitas (probability density) adalah dihitung dengan rumus peluang : interval 0,975 - 0,979 V = peluang = 1/50 = 0,02; kepadatan prob.= 0,02 : 0,005 = 4
0,980 - 0,984 V = peluang = 3/50 = 0,06; kepadatan prob.= 12 0,985 - 0,989 V = peluang = 0,04; kepadatan prob.= 8 0,990 - 0,994 V = peluang = 0,14; kepadatan prob.= 28 0,995 - 0,999 V = peluang = 0,24; kepadatan prob.= 48 1,000 - 1,004 V = peluang = 0,2; kepadatan prob.= 40 1,005 - 1,009 V = peluang = 0,16; kepadatan prob.= 32 1,010 - 1,014 V = peluang = 0,06; kepadatan prob.= 12
𝑝(𝑖) =
𝑁𝑖1,015 - 1,019 V =peluang = 0,02; kepadatan prob.= 4 1,020 - 1,024 V = peluang = 0,04; kepadatan prob.= 8 1,025 - 1,029 V = peluang = 0,02; kepadatan prob.= 4 Histogram kepadatan probabilitasnya adalah:
Gambar histogram kepadatan probabilitas Untuk menghitung rata-rata output dari data kelompok dapat digunakan rumus:
adalah rata-rata output adalah frekuensi interval adalah nilai tengah interval
Nilai tengah dari masing-masing interval dan frekuensinya adalah:
0,977 V; frekuensi = 1; 0,977 x 1 = 0,977 0,982 V; frekuensi = 3; 0,982 x 3 = 2,946 0,987 V; frekuensi = 2; 0,987 x 2 = 1,974 0,992 V; frekuensi = 7; 0,992 x 7 = 6,944 0,997 V; frekuensi = 12; 0,997 x 12 = 11,964 1,002 V; frekuensi = 10; 1,002 x 10 = 10,02 1,007 V; frekuensi = 8; 1,007 x 8 = 8,056 1,012 V; frekuensi = 3; 1,012 x 3 = 3,036 1,017 V; frekuensi =1; 1,017 x 1 = 1,017 1,022 V; frekuensi = 2; 1,022 x 2 = 2,044
= 𝑂 ¯
Σ ⋅𝑓Σ𝑓𝑖𝑥𝑖𝑖
𝑂 ¯ 𝑓
𝑖𝑥
𝑖1,027 V; frekuensi = 1; 1,027 x 1 = 1,027
Dari perhitungan di atas diperoleh rata-rata kelompok adalah 1,0001 dan standar deviasinya adalah 0,01. Perhitungannya dapat dilihat di sini.
Gambar kurva distribusi normal dari rata-rata 1,0001 dan standar deviasi 0,01
1.7. Model statik elemen sistem pengukuran
Jika histerisis dan resolusi dapat diabaikan, maka model output elemen sistem pengukuran adalah:
;
Sehingga model statik elemen sistem pengukuran yang dikaitkan dengan model dinamik dapat diilustrasikan oleh gambar berikut.
Gambar model statik elemen pengukuran
𝑂 = 𝐾𝐼 + 𝑎 + 𝑁(𝐼) + 𝐾
𝑀𝐼
𝑀𝐼 + 𝐾
𝐼𝐼
𝐼1.8. Ringkasan
1. Tujuan sistem sensor atau sistem pengukuran adalah menjadi penghubung informasi dari proses ke pengamat;
2. Kinerja sistem pengukuran ditentukan oleh error yang dihitung dari selisih antara MV dan TV;
3. Sistem pengukuran terdiri atas empat tipe elemen: sensing, signal conditioning, signal processing, dan data presentation;
4. Karakteristik statik elemen terdiri dari karakteristik sistematik dan karakteristik statistik;
5. Pengukuran karakteristik statistik dilakukan menggunakan standar prosesnya dinamakan kalibrasi.
1.9. Latihan
1. Sebuah termokopel digunakan pada rentang suhu 0 dan 500°C dan memiliki data input-output sebagai berikut:
Input T °C 0 100 200 300 500
Output E µV 0 5268 10777 16325 27388 Tentukan persamaan garis lurus idealnya!
Tentukan noliniearitas pada 100°C dan 300°C dalam µV dan dalam persentase f.s.d!
2. Sebuah sensor gaya memiliki rentang input 0 sampai 10 kN dan output 0 sampai 5 V pada kondisi suhu standar 20°C. Pada suhu 30°
rentang output menjadi 0 sampai 5,5 V.
Tentukan apa saja efek lingkungan yang teridentifikasi!
2. Akurasi Sistem dalam Kondisi Tunak
Bab sebelumnya membahas karakteristik statik pada sebuah elemen sistem pengukuran dan mendefinisikan error sebagai selisih antara Measured Value (MV) dan True Value (TV). Bab ini membahas cara menghitung output dan error pengukuran dari keseluruhan sistem pengukuran yang terdiri dari beberapa elemen. Selain itu kita juga akan membahas metode-metode yang dapat digunakan untuk mengurangi error sistem pengukuran.
2.1. Capaian pembelajaran
Setelah mempelajari bab ini, mahasiswa akan mampu
1. Menghitung akurasi sistem pengukuran pada steady state (tunak);
2. Menyebutkan teknik-teknik reduksi error.
2.2. Error sistem ideal
Mari kita tinjau sistem pengukuran yang tersusun atas n elemen ideal dan terangkai secara seri. Diasumsikan tidak ada pengaruh lingkungan dan bias, a = 0. Pada sistem tersebut, untuk elemen ke-i berlaku:
di mana i = 1, ..., n; O adalah output elemen ke-i; K adalah sensitivitas elemen ke-i; dan I adalah input untuk elemen ke-i.
Untuk elemen ke-2 berlaku hubungan:
;
Untuk elemen ke-3 berlaku hubungan:
;
Untuk seluruh sistem berlaku hubungan:
.
Hubungan tiap elemen digambarkan dalam bentuk diagram berikut ini:
Gambar diagram elemen ideal sebagai penyusun sistem pengukuran Error sistem pengukuran diberikan oleh persamaan:
, atau
Sehingga untuk elemen ideal, agar E = 0, maka harus sama dengan 1.
( 𝐼
𝑀= 𝐼
𝐼= 0)
= 𝑂
𝑖𝐾
𝑖𝐼
𝑖i i i
= = 𝐼
𝑂
2𝐾
2𝐼
2𝐾
2𝐾
1= = 𝐼
𝑂
3𝐾
3𝐼
3𝐾
3𝐾
2𝐾
1𝑂 = 𝑂
𝑛= 𝐾
1𝐾
2𝐾
3… … 𝐾
𝑖𝐾
𝑛𝐼
𝐸 = 𝑂 − 𝐼
𝐸 = ( 𝐾
1𝐾
2𝐾
3… 𝐾
𝑛− 1)𝐼
…
𝐾
1𝐾
2𝐾
3𝐾
𝑛2.3. Error sistem non ideal
Untuk sistem pengukuran yang tersusun atas elemen-elemen tidak ideal, maka lingkungan dan nonlinearitas elemen memberi pengaruh kepada persamaan karakteristik sistematik dan statistik dari seluruh sistem. Rata-rata output pada masing-masing elemen dapat
diaplikasikan untuk menghitung rata-rata output dari sistem pengukuran. Standar deviasi output sistem dihitung berdasarkan standar deviasi output dari masing-masing elemen. Rata-rata error dihitung dengan mengurangi rata-rata output terhadap rata-rata input. Standar deviasi error dihitung dari standar deviasi output saja, karena standar deviasi input adalah sama dengan nol.
Langkah-langkah untuk menghitung rata-rata error sistem pengukuran dan standar deviasi error adalah sebagai berikut:
1. Hitung rata-rata output sistem pengukuran dengan cara menghitung rata-rata output dari masing-masing elemen. Rata-rata output masing-masing elemen tergantung model masing-masing elemen;
2. Hitung rata-rata error dengan cara ;
3. Hitung standar deviasi output sistem pengukuran berdasarkan standar deviasi masing-masing elemen;
4. Tetapkan standar deviasi output sebagai standar deviasi error.
Namun demikian ada dua model perhitungan rata-rata error dan standar deviasi error dari sistem pengukuran.
1. Menggunakan model umum elemen sistem pengukuran pada kondisi tunak. Model ini menggunakan persamaan atau menggunakan model output khusus dari elemen;
2. Menggunakan model pita error. Pada model ini, output elemen digambarkan dalam pdf berbentuk segi empat dengan lebar 2h yang mengapit garis lurus ideal tepat di tengah-tengahnya.
Menghitung dan menggunakan model pertama
Gambar berikut ini memperlihatkan bagaimana output sistem dihitung berdasarkan output dari masing-masing elemen. Terlihat bahwa output elemen terakhir menjadi output dari sistem. Output sebuah elemen menjadi input bagi elemen berikutnya. Input elemen ke-1 adalah True Value of Variable. dan dianggap memiliki 𝝈 = 0.
Gambar perhitungan error menggunakan model pertama Rata-rata output elemen ke-i sampai ke-n adalah:
;
; ...
; .
Rata-rata error sistem adalah:
.
Standar deviasi E = dikarenakan .
Standar deviasi output elemen ke-i sampai ke-n dihitung dengan cara sebagai berikut:
;
; ...
;
= −
𝐸 ¯ 𝑂 ¯ 𝐼 ¯
= + + + +
𝑂 ¯ 𝐾 ¯ 𝐼 ¯ 𝑎 ¯ 𝐾 ¯
𝑀𝐼
𝑀¯ 𝐼 ¯ 𝐾 ¯
𝐼𝐼 ¯
𝐼𝑁(𝐼) ¯
= +
𝑂 ¯ 𝐾 ¯ 𝐼 ¯ 𝑎 ¯
𝐸 ¯ 𝜎 𝐸
I
= + + + + =
𝑂 ¯
1𝐾 ¯
1𝐼 ¯
1𝑎 ¯
1𝐾
𝑀¯
1𝐼
𝑀¯
1𝐼 ¯
1𝐾 ¯
𝐼1𝐼
𝐼¯
1𝑁( ) ¯ 𝐼
1𝐼 ¯
2= + + + + =
𝑂 ¯
2𝐾 ¯
2𝐼 ¯
2𝑎 ¯
2𝐾
𝑀¯
2𝐼
𝑀¯
2𝐼 ¯
2𝐾 ¯
𝐼2𝐼
𝐼¯
2𝑁( ) ¯ 𝐼
2𝐼 ¯
3= + + + + =
𝑂
𝑛−1¯ 𝐾
𝑛−1¯ 𝐼
𝑛−1¯ 𝑎
𝑛−1¯ 𝐾
𝑀¯
𝑛−1𝐼
𝑀¯
𝑛−1𝐼
𝑛−1¯ 𝐾
𝐼¯
𝑛−1𝐼
𝐼¯
𝑛−1𝑁( 𝐼 ¯
𝑛−1) 𝐼 ¯
𝑛= + + + + 𝑁( ) =
𝑂 ¯
𝑛𝐾 ¯
𝑛𝐼 ¯
𝑛𝑎 ¯
𝑛𝐾 ¯
𝑀𝑛𝐼 ¯
𝑀𝑛𝐼 ¯
𝑛𝐾 ¯
𝐼𝑛𝐼 ¯
𝐼𝑛𝐼 ¯
𝑛𝑂 ¯
= −
𝐸 ¯ 𝑂 ¯ 𝐼 ¯
=
𝜎
𝐸𝜎
𝑂𝜎
𝐼= 0
= + + + + + + =
𝜎
𝑂21( )
𝛿𝑂𝛿𝐾112
𝜎
𝐾21( )
𝛿𝑂𝛿𝐼112
𝜎
2𝐼1( )
𝛿𝑂𝛿𝑎112
𝜎
2𝑎1 (𝛿𝐾𝛿𝑂𝑀11)2𝜎
𝐾2𝑀1 (𝛿𝐼𝛿𝑂𝑀11)2
𝜎
2𝐼𝑀1 (𝛿𝐾𝛿𝑂𝐼11)2
𝜎
𝐾2𝐼1 (𝛿𝐼𝛿𝑂𝐼11)2
𝜎
2𝐼𝐼1
𝜎
𝐼22= + + + + + + =
𝜎
𝑂22( )
𝛿𝑂𝛿𝐾222
𝜎
𝐾22( )
𝛿𝑂𝛿𝐼222
𝜎
2𝐼2( )
𝛿𝑂𝛿𝑎222
𝜎
2𝑎2 (𝛿𝐾𝛿𝑂𝑀22)2
𝜎
𝐾2𝑀2 (𝛿𝐼𝛿𝑂𝑀22)
2
𝜎
2𝐼𝑀2 (𝛿𝐾𝛿𝑂𝐼22)
2
𝜎
𝐾2𝐼2 (𝛿𝐼𝛿𝑂𝐼22)
2
𝜎
2𝐼𝐼2
𝜎
𝐼23= + + + + + + = =
𝜎
𝑂2𝑛( )
𝛿𝑂𝛿𝐾𝑛𝑛2
𝜎
𝐾2𝑛( )
𝛿𝑂𝛿𝐼𝑛𝑛2
𝜎
2𝐼𝑛( )
𝛿𝑂𝛿𝑎𝑛𝑛2
𝜎
𝑎2𝑛 (𝛿𝐾𝛿𝑂𝑀𝑛𝑛 )2
𝜎
2𝐾𝑀𝑛 (𝛿𝐼𝛿𝑂𝑀𝑛𝑛)2
𝜎
𝐼2𝑀𝑛 (𝛿𝐾𝛿𝑂𝐼𝑛𝑛)2
𝜎
𝐾2𝐼𝑛 (𝛿𝐼𝛿𝑂𝐼𝑛𝑛)2