A theoretical study was performed on the effect of imperfections on the buckling load of a circular cylindrical shell under axial compression. The reader is referred to Fung and Sechler (Ref. 1) for a detailed discussion and listing of some of the many writings on this subject. For a discussion of the role of imperfections in shell buckling, the reader is referred to Arbocz and Babcock (Ref. 2).
The work presented herein represents a reinforcement of the theory presented by Arbocz and Babcock. A study of the influence of these assumptions on the resulting algebraic equations is one goal of this work. Begin with the axis assumptions made in deriving the nonlinear shell equations of Donnell (Ref. 5) that one may choose to use.
Then there are differences in the m.method, depending on the specific way in which the periodicity of the circumferential reference displacement is fulfilled. The Galerkin procedure used by Arbocz and Babcock (and others) left open the mathematical validity of the specific weighting function to be used - an essential and all-important factor in the analysis.

THEORETICAL FORMULATION
Note that the periodicity of the circumferential displacement is satisfied without the need to introduce a homogeneous solution as required in the stress function approach (ref. 4). It should be noted that the many trigonometric forms resulting from different products do not contribute to the total potential energy. A comparison of these equations with those of Arbocz and Babcock (Ref. 2) will reveal that they are identical if the meaning is reversed.
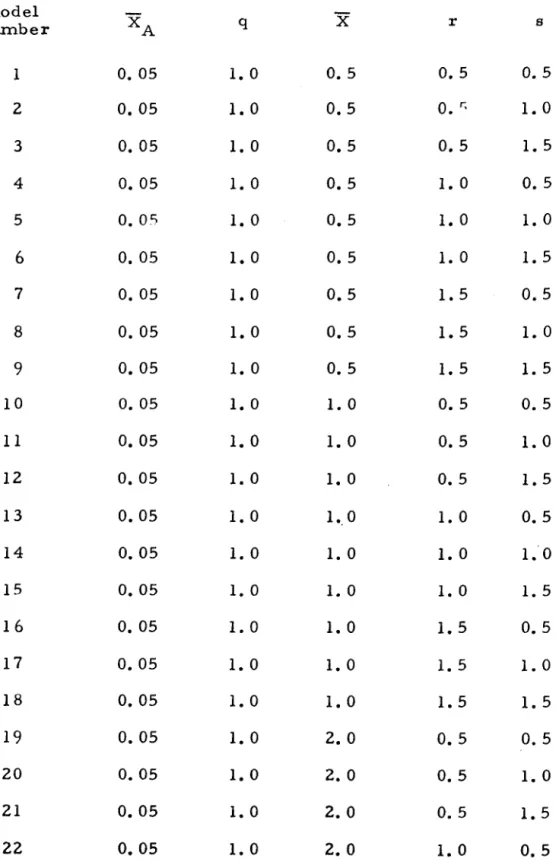
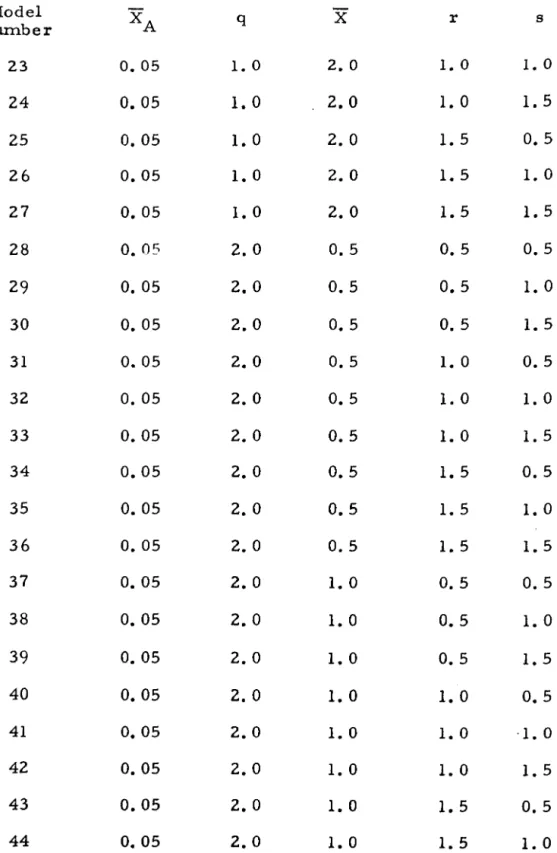
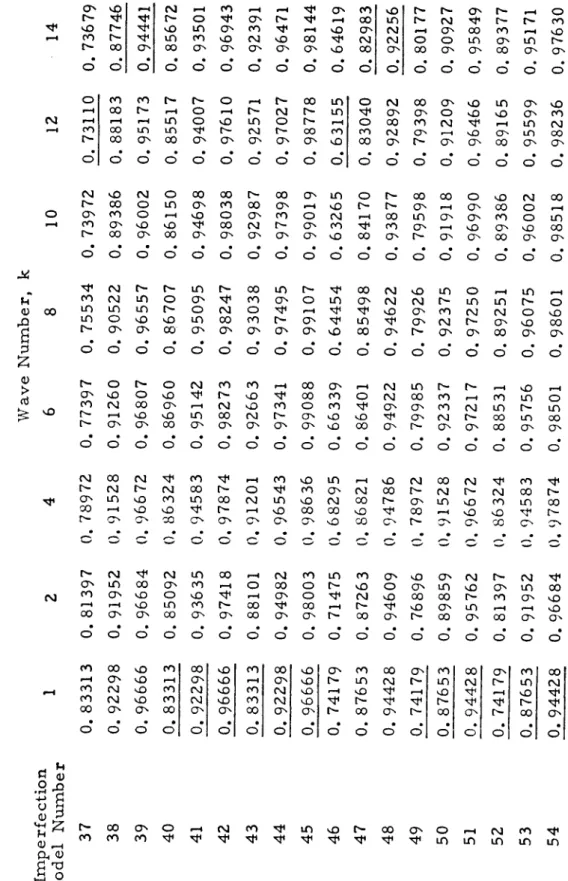
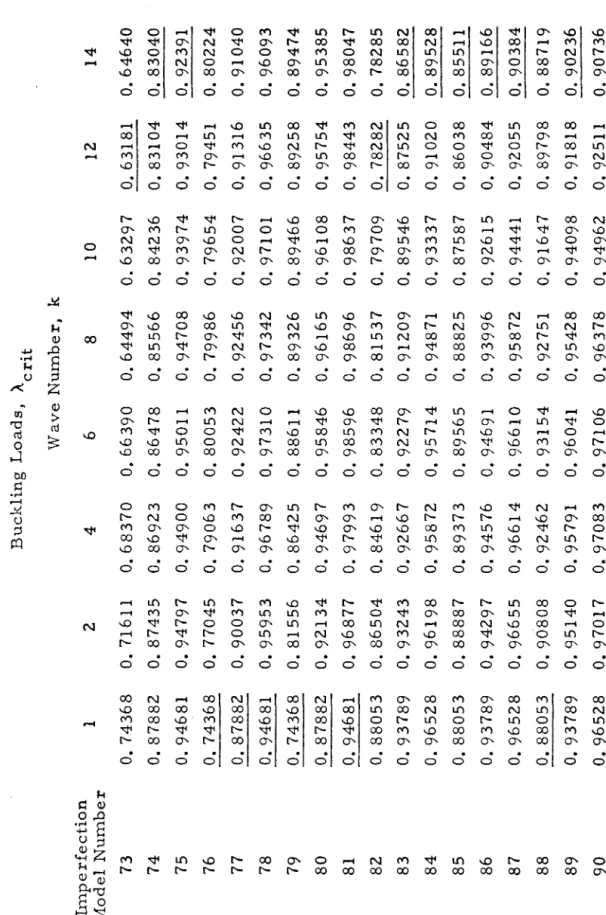
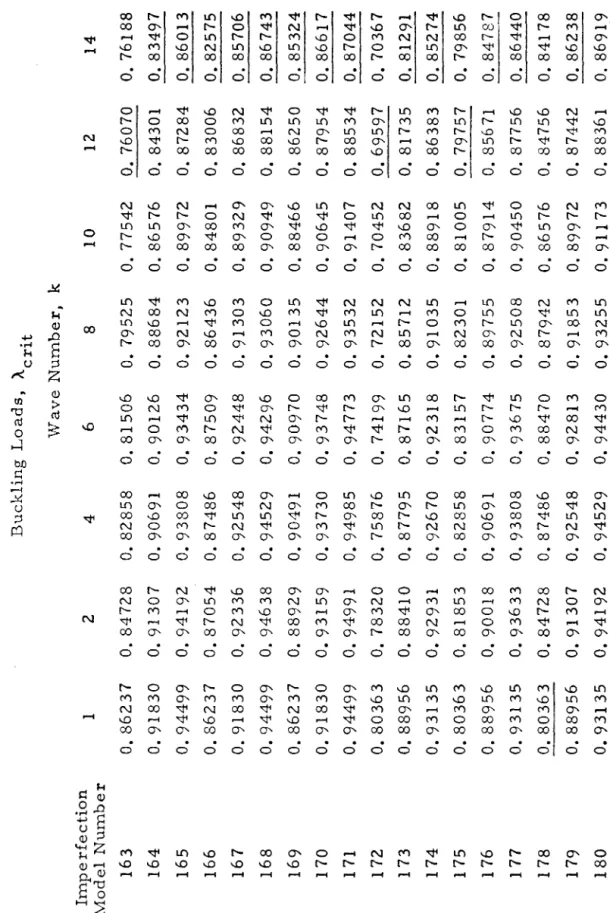
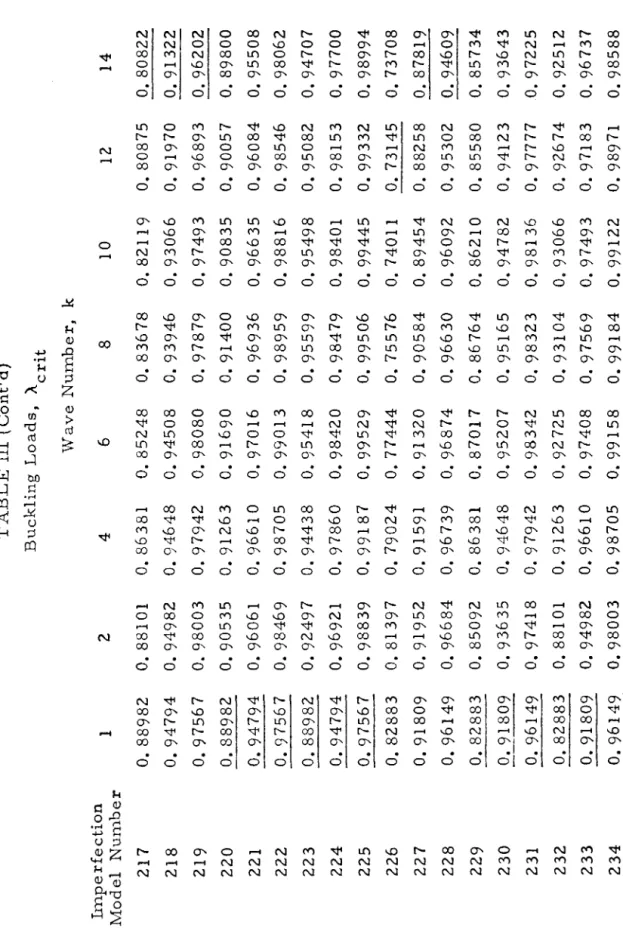
Throughout the numerical analysis, the geometry and material properties of the shell were kept constant. The Koiter circle is defined by the relationship. with the restriction that for positive, nonzero i. This value was then used to calculate all the coefficients of the bending equations. k and 13 were such that they were very close but not exactly in the Koiter circle.
Expressions for the lfJ· terms are given below. the expression for displacement amplitude Sl' the second bending equation can be written as a cubic polynomial in A:. Since the im.perfection amplitudes are given by equations 32 and 33, and the m.ode para.eter forms are defined as in the paragraph.
DISCUSSION OF NUMERICAL RESULTS AND RECOMMENDATIONS
For a given asym.m.etric model, changes in the axis ym.m.etric model do not change the sensitivity of the shell to long- versus short-wave imperfections. In the range of values chosen for X, changes in this parameter reduce the buckling load but do not affect the sensitivity of the shell to long- versus short-wavelength imperfections. Only in those cases where the yrn.m.etric imperfection of the axis is small and decays quickly (X.
In other cases, since s is the decay rate that on the circle.ferential wavenumber i. work, and since 1 differs from. 1 ° to 27, a high value of s tends to make the asirn.m.etric imperfection amplitude nearly equal to the asirn.- m.etric imperfection amplitude. For the asym.m.etric m.ode1 the decay rate r acts on the axial wave nurn.ber, k, varying from.
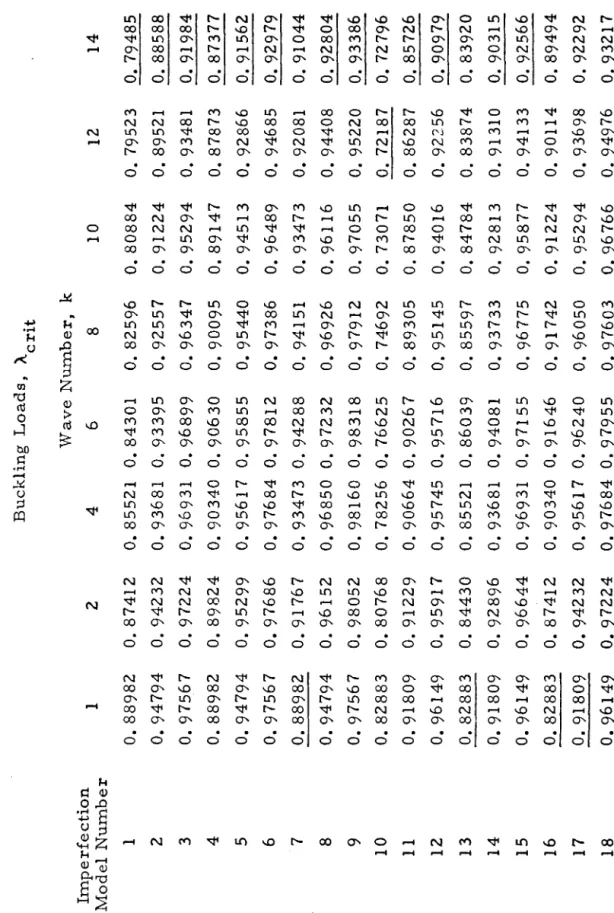
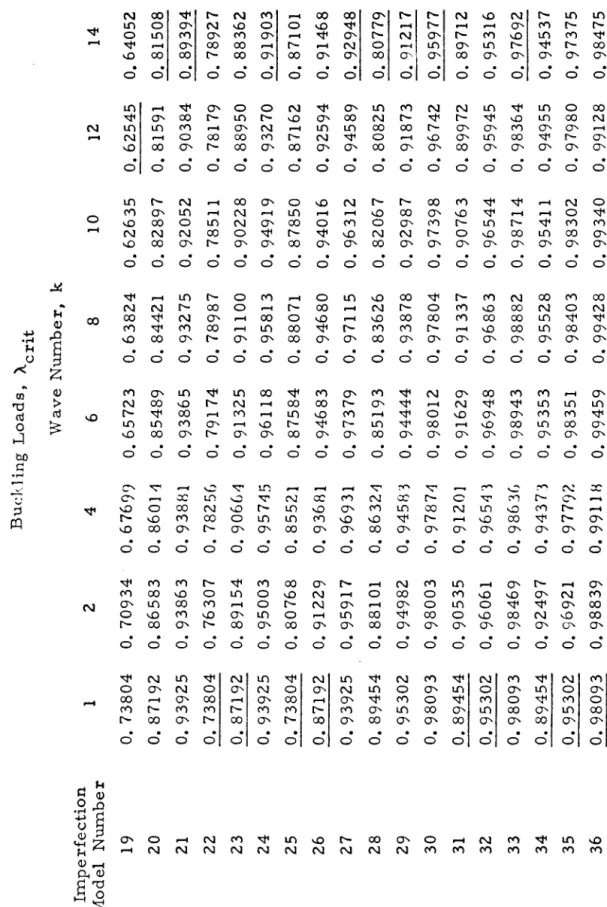
The decay rate s acts on the circumferential wave nurn.ber, 1, which in this case varies from . 5, the effect is even greater, because the decay at the circumferential wavenumber is much greater than that at the axial wavenumber. As can be seen in Figures 9 through 20, buckling is always dominated by shortwave imperfections, regardless of the variations of the other four parameters, when the decay of asymmetric imperfections with an axial wavenumber is relatively low (r = 0.5).
If the decay of asymmetric imperfections with increasing axial wavenumber is relatively slow (r = 0.5), then buckling is dominated by short-wave imperfections. If the asymmetric imperfections are large and decay slowly compared to the asymmetric imperfections, then shortwave imperfections dominate (compare figures 19 and 20 with figures 13 and 14). If the asymmetric imperfections are nearly equal in size to the asymmetric imperfections, then buckling is dominated by shortwave imperfections.
The important parameter to make the axisymmetric imperfection have a significant value is the decay rate q. If the decay of axisymmetric imperfections with increasing axial wavenumber in this state is relatively high (q and the decay of the asymmetric imperfections is high ( r, then cracking. With large axisymmetric imperfections decay slowly with the wave) number, it is necessary to have large asym .m.etric imperfections that decay rapidly with axial wavenumber and slowly with circumferential-.
26- 7. Sununa ry
However, in this range of r the behavior is sensitive to all other parameters in the model and the effects must be selected carefully. The numerical data generated for this study indicate that further investigation of the decay rate parameters would be enlightening. It is clear that one can interpolate between the obtained curves to obtain information about the behavior of shells with different values of the parameters X A and X within the range of values used here, and that the parameter q is relatively uninteresting (if it is more greater than one ).
However, more attention could be paid to the decay rates of rand s, especially given the fact that the experimentally derived values for these parameters are widely scattered between values of 1. It is evident that the nature of the sensitivity of the shell to imperfections changes quite rapidly in this range of these parameters.
APPENDIX I Operator Coefficients
APPENDIX IV
In all cases, the sign of the asymmetric imperfection is positive (outward) while the asymmetric imperfection is always negative (inward). Refer to Table II for description of the imperfection nodule corresponding to the listed m.odel number. Solve compatibility equations (stress function) Satisfy periodicity of v Use the stress's function methods of solution.