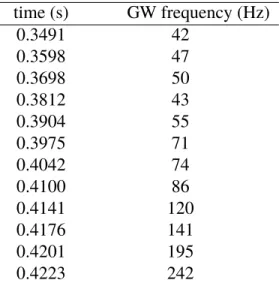
Introduction
Black Hole’s Hair in Modified Gravity
The second term vanishes as a result of the Brans-Dicke field equation in the conformal frame. When the scalar field is constant, the Brans-Dicke field equation reverts to the Einstein field equation.
Black Hole’s Hair in Quantum Mechanics
The only possibility is that the scalar energy is radiated away during black hole formation from gravitational collapse. However, the temperature is determined by the surface gravity, which is solely dependent on the three hairs of black hole.
Quantum Hair Near the Event Horizon and Gravitational Wave Echoes
In this paper we focus on the SGWB in the transverse scalar mode of the Brans-Dicke (BD) theory: identifying its astrophysical origin, and obtaining its energy spectrum (as a function of the BD coupling constant). The energy density of the scalar GW ρS is related to the scalar stress-energy tensorTSµν viaρS =TS00, with.
Gravitational Wave Memory: A New Approach to Study Modified
Introduction
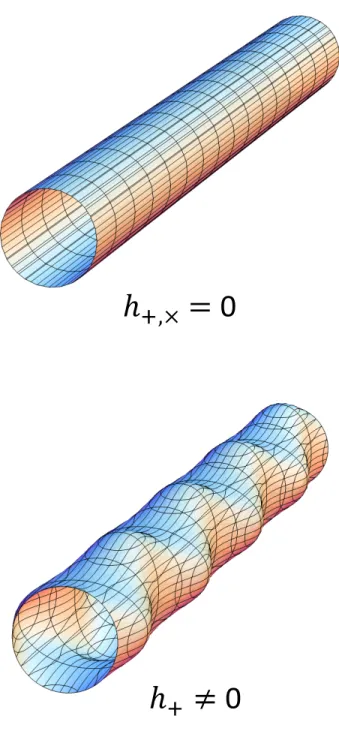
In this letter, we will show that both goals can be achieved using gravitational wave memory. The gravitational wave memory is a permanent change in spacetime geometry, which in general relativity (GR) is a jump in the transverse traceless part of the spacetime metric ∆hTTi j before and after a burst event [45].
T memory and S memory in scalar-tensor gravity
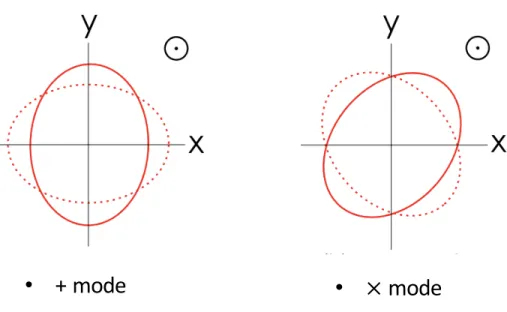
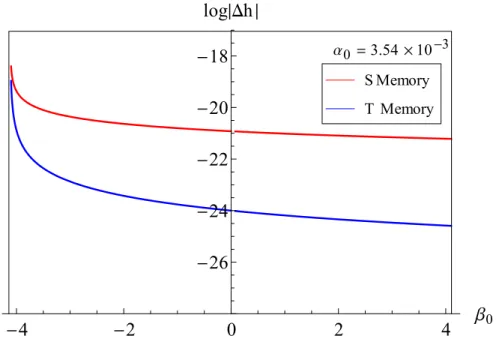
We will then point out that the no-scalar hair property of black holes in scalar-tensor theories will give rise to the S-memory, a scalar component of gravitational wave. We will refer to the +,× modes as tensor (T) modes, and the◦ mode as the scalar (S) mode.
Analytic results of a simplified model
Previous numerical simulations [85, 117] indicate that scalarization changes the asymptotic value of the scalar field profile from δφH ∼ α02M/r to δφH ∼ α0M/r. Thus, for α0 ∼ 10−3, the scalar field profile for a scalarized star is improved by about 3 orders of magnitude.
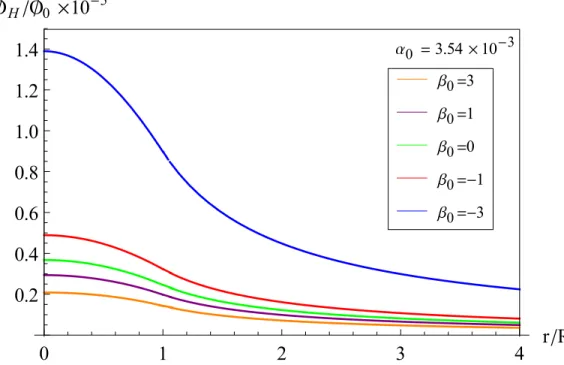
Detection Strategies
The coefficient arises from the angular portion of the integral and as a result of the asymmetric distribution of the scalar field profile. We describe the dependence of the SNR on the direction of the source by introducing the N-detector effective angular pattern function FN(Ω)ˆ and is given by FN(Ω)ˆ = [ ®α ®F◦(Ω)]ˆ 2 / ®α2.
Discussions
Acknowledgements
Appendix A: Scalar-tensor theory of gravity, scalar gravitaional wave
To study the gravitational wave solution and its polarizations, we linearize the fields gµν and φand start from the linearized field equations:. 2.39). When a specific coordinate is chosen, it is not possible to perform a global Lorentz transformation without changing the basis vectors.
Appendix B: Detection strategy for scalar gravitational wave memory
To maximize the signal-to-noise ratio, the optimal filtering function ˜Q(f) should be. First, we need to specify the unit vectors pointing along the two arms of these detectors.
Appendix C: Detection strategy for scalar gravitational wave memory
For the scalar memory of gravitational waves, ˜Φ(f)= 2πiΦI f−i1 and for convenience we take the noise spectra of the four detectors as the same. The maximized angular pattern function F (Ω)ˆ = F®S0(Ω) · ®ˆ FS0(Ω)ˆ as a function of latitude θ and longitude ϕ (F (Ω)ˆ is independent of the angle ψ) by correlating HLV and HLVK detectors are presented in.
Appendix D: Gravitational Collapse in Oppenheimer-Snyder model . 49
We study the stochastic scalar gravitational wave background (SGWB) from astro-physical sources, including compact binary mergers and stellar collapses, in Brans-Dicke gravity theory. This is because unlike tensor radiation, which mainly starts from quadrupole order, scalar perturbation can be excited by changes in the monopole moment.
Introduction
In contrast to tensor waves, we found that the scalar SGWB is mostly generated by stellar collapses. II, we will give an overview of the scalar GW in Brans-Dicke theory and its connection with the scalar SGWB.
Scalar GW in Brans-Dicke Theory and Relation to SGWB
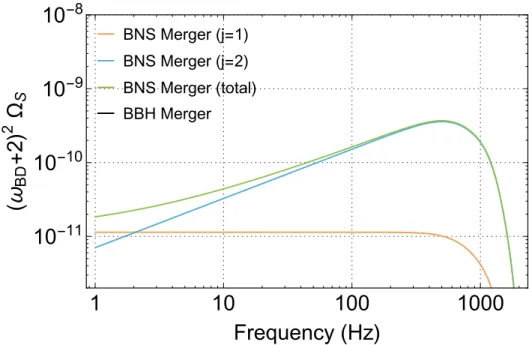
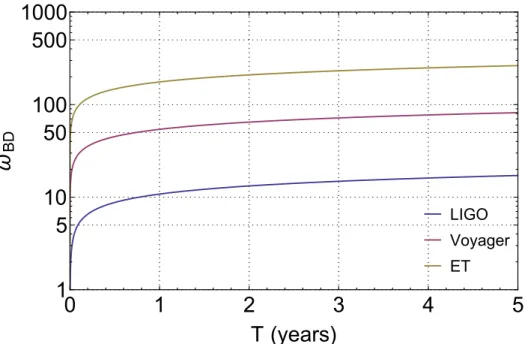
According to this definition, ˜HS is related to the scalar spectral density ˜ΩSGW [Defined in Eq. Thus, even though ˜ΩS is directly proportional to the energy density of the scalar wave, the background detectability, given the same ˜ΩS, still depends on the BD coupling constant of the couplingωBD.
Scalar and Tensor SGWB from Mergers of Compact Binary System . 56
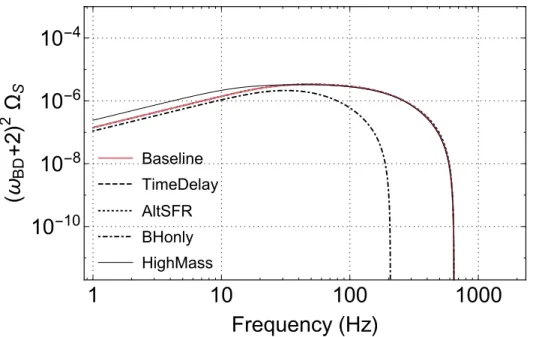
As for the scalar part, the story is completely different: the contribution to the scalar SGWB from the mergers of BBH is exactly zero. At the reference frequency f = 25 Hz, HighMass predicts a value of ΩS that is 1.1 times the baseline value, while BOnly predicts 0.7 the baseline value.
Detectability
Next, we will explore the detectability of Advanced LIGO at its designed sensitivity and the planned future ground-based GW detectors. The scalar overlap reduction function between the detectors at Hanford and Livingston is calculated, where we adopt the normalization convention as [51].
Conclusions and Discussions
71], in such models the scalar memory, which dominates scalar radiation during collapse, can be significantly enhanced by such dependencies through scalarization [69], thus can lead to much stronger SGWB amplified by several orders of magnitude [85, 117]. In this case, we expect a significant increase in the detectability of the current and the next generation detectors.
Acknowledgements
Appendix A: Scalar Overlap Reduction Function For Einstein Telescope 68
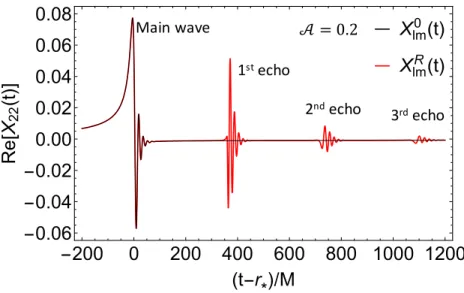
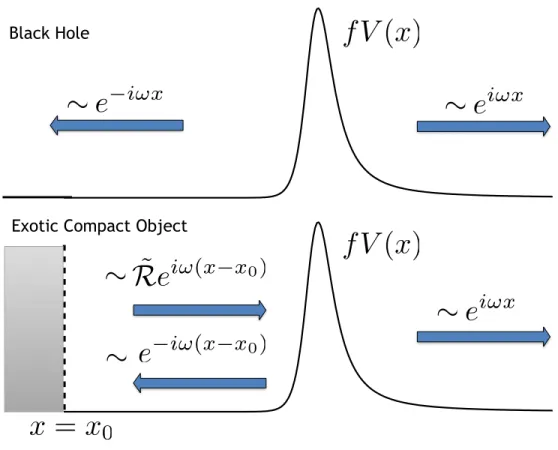
We show how to reprocess radiation in the near-horizon of a Schwarzschild black hole to the asymptotic radiation from the corresponding source in an ECO spacetime. We find that the quasinormal mode ringing in the black hole spacetime plays a central role in determining the shape of the first few echoes.
Introduction
Price and Khanna hypothesized that the echoes can be considered as a superposition of ECO resonant modes [126]. We find that the ECO waveform can be constructed from the BH waveform and a reprocessed version of the waveform observed at the BH horizon.
Waves near a compact object
Having defined these amplitudes, we can, in the presence of the reflecting boundary ˜gref of Eq. 4.11) to calculate the asymptotic amplitude associated with scalar waves ˜ψ,. This shows that the waveform seen by distant observers can be understood as the sum of the ordinary emission in a BH spacetime, together with an additional signal ˜KZBHH.
Examples of Echoes
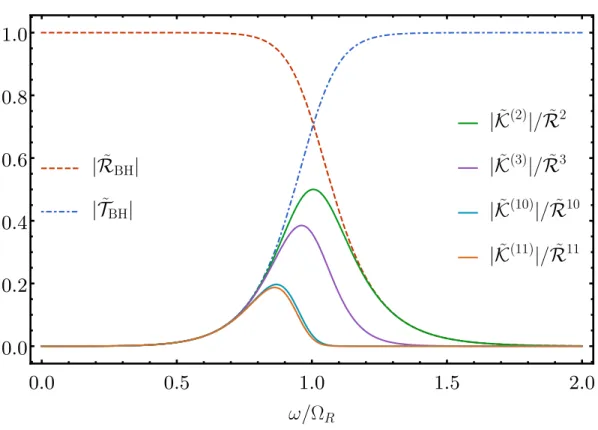
We divide the response functions by ˜Rn to rescale them and shift each by 2n|x0|so that they overlap. the transfer function slows down so that there is very little difference between the 10th and 11th echoes. A comparison of the first echoes and the fifth echoes produced by a test payload following the ISCO dive trajectory is shown in Fig.
Excitation of ECO Modes
Imaginary part (`,m)=(2,2)of the total waveform ψ∞ excited by the test charge after the ISCO plunging orbit. Imaginary part (`,m)= (2,2), time domain, total waveform excited by test charge after ISCO plunging orbit.
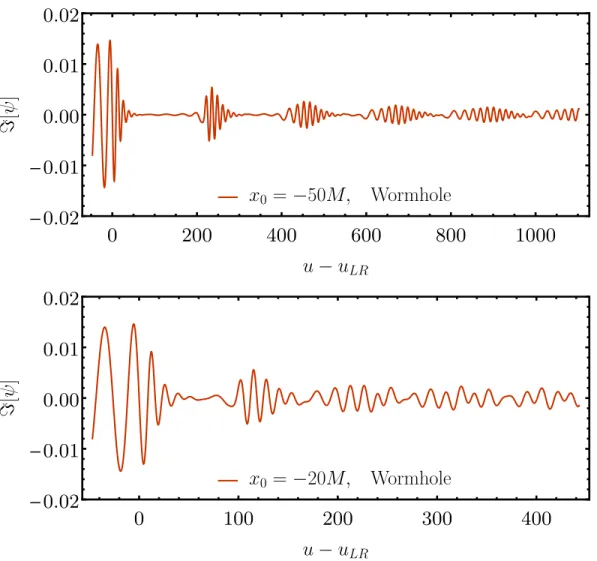
General Features of echoes
4.20, reveals that the template lacks key features of the horizon waveform at low frequencies|ω| < ΩR. For perfectly reflective, extremely compact ECOs with x0 > 20M, more than 97% of the energy in the horizon waveform is radiated in echoes.
Conclusions
To determine the significance of our proposed template, future work will be required to extend the formalism to gravitational perturbations of Kerr. Ideally, future work will also extend the formalism beyond test particle sources so that comparable mass binaries can be treated.
In addition to the added algebraic complexity, the lack of Birkhoff's Kerr theorem will have to be overcome, as well as the lack of a simple scheme for parametrizing the reflective boundary conditions for gravitational perturbations [126] (see [112] for a possible description). . However, our results show that a relatively simple template, combined with a recipe for reprocessing waveforms generated in black hole spacetime, can be used to probe the existence of ECOs and their echoes using gravitational wave observations.
Appendix A: Calculation of the reflection and transmission coefficients103
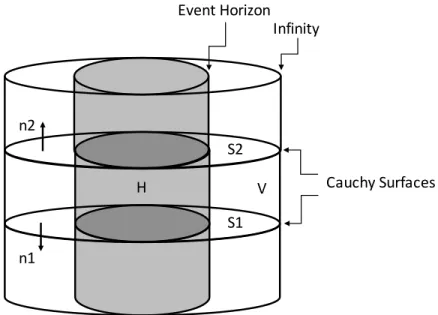
Note that the field at the horizon is not determined by the initial conditions in the near horizon matching area. We obtain the delayed Green's function gBH for the scalar field in BH spacetime as the solution of a characteristic initial value problem.
Appendix C: Wormhole Reflectivity
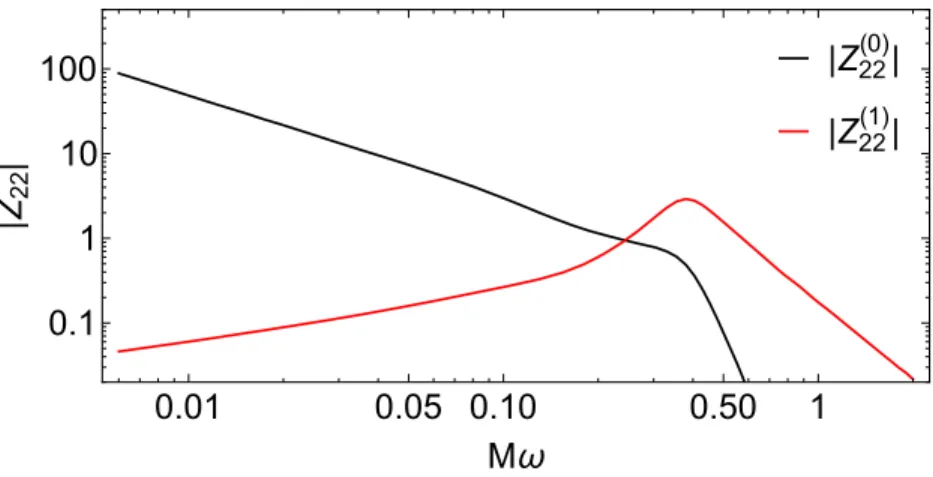
We obtain the frequency-domain horizon waveform ZBHH by numerically performing the inverse Fourier transform of the time-domain waveform ψBHH. In the left half of the universe, ˜ψup(−y) is the solution that describes waves that are completely outgoing at zero-infinity.
Appendix D: Fourier Transform of Decaying Sequence of Pulses
This robustness indicates that the area below the Planck potential is the most relevant observable of the near-horizon structures in SGWB. Another information from the observation is the peak amplitude of the voltage, which marks the end of the inspiratory phase.
Searching for near-horizon quantum structures in the binary black-
Introduction
In this letter, we propose to search for near-horizon structures through the stochastic GW background (SGWB) of BBH mergers. Because the echo contribution to the background depends only on their energy spectra, it is much less sensitive to details of echo generation, making the method more robust to uncertainties in the near-horizon structures.
GW amplitudes and power emitted
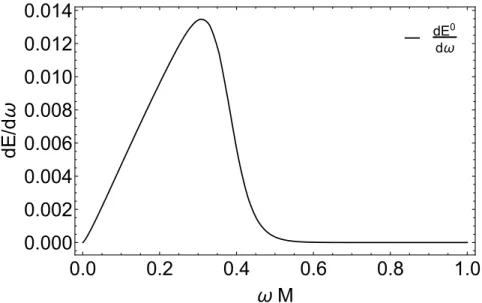
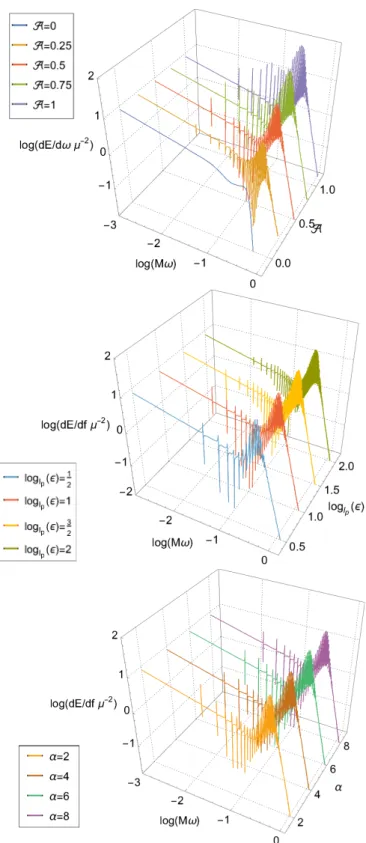
We estimate the magnitude and coarseness of this SGWB and illustrate its dependence on the near-horizon structure, following an effective one-body (EOB) approach: the two-body dynamics and waveform are approximated by the plunge of a point particle towards a Schwarzschild BH following a trajectory that smoothly transitions from inspiratory to dive [49. The GW energy spectrum is given by dE/dω =Õ. 5.7) For BHs, forcing incoming boundary condition near the horizon and outgoing condition near zero infinity, solution to Eq.
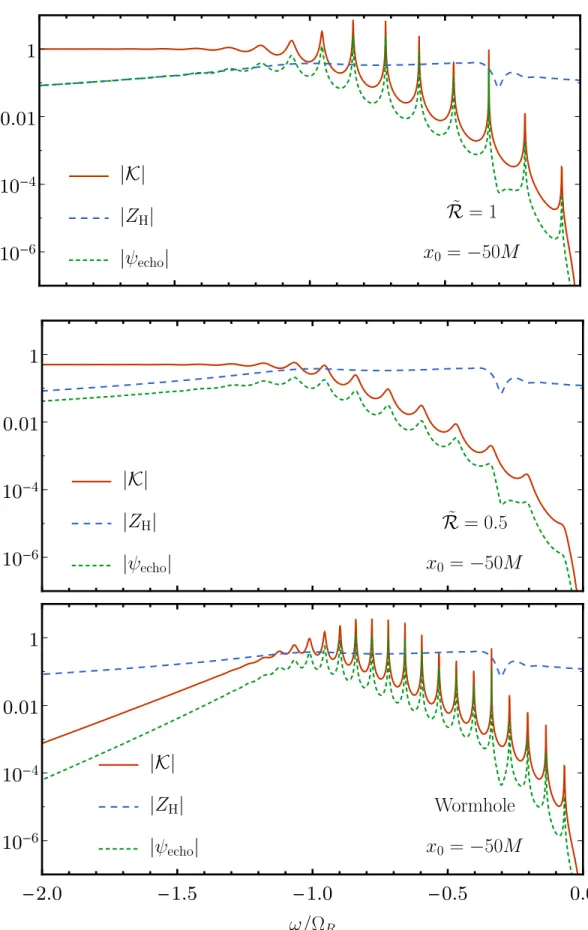
Echoes from near-horizon structure
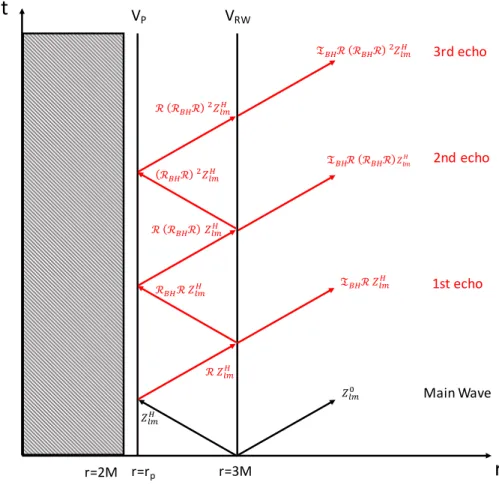
This is the sum of energies from the main wave, the first echo and the beat between the main wave and the first echo. While the beat is linear inR, it is highly oscillatory inω, since the main wave and the echo are well separated in the time domain.
Models of Reflectivity and Energy Spectra of Echoes
These resonant peaks are related to the poles of 1/(1− RRBH) in the series sum of Eq. In the left panel, we choose several different values that lead to different peak separation at low frequencies.
Stochastic Gravitational-Wave Background (SGWB)
In the right panel we consider reflectivity (5.28) and find that the shape of the Planck potential, as characterized by α, has negligible influence on dE/dω as long as the area remains fixed. For A ~ 1, we obtain significant additional SGWB from the echoes (left panel of Fig. 5.4) in a way that is insensitive to the location and shape of the near-horizon structure, as characterized by andα (right panel).
Detectability
We use the confidence model described in [18], where Rm(z) is proportional to the star formation rate with metallicity Z < Z/2 and slows with the time between BBH formation and merger. For smaller A we plot the additional SGWB, defined as lPM: beat between the main wave and the echoes Eq. 5.21) is unimportant, and the additional SGWB arises mainly from energy contained in the first echo.
Conclusions and Discussions
Uncertainties also exist in the SGWB of the main wave, arising, for example, from different star formation rates, different metallicity thresholds to form BHs, details in binary star evolution, and the distributions in the time lag between BBH formation. and fusion – all this leads to uncertainties in the local BBH fusion rate and the local distribution of mass M and symmetrical mass ratio v [18]. However, seeking matched filtering of individual signals requires the exact waveform, which in our model depends not only on A, but also on andα, but may further depend on other unknown details of the Planck-scale potential – making it less becomes robust.
Acknowledgements
Our result shows that the appearance of near-horizon structures changes the slfaope Ω(f), causing it to deviate from the f2/3 power law even at low frequencies. Within the bandwidth of ground-based GW detectors, this background arises solely from the inspiral, which gives a power law of f2/3 and is unaffected by the presence of near-horizon structure.
Linearized Einstein field equation
cf. (A.9) is the so-called linearized Einstein field equation, where µν is the stress-energy tensor for the gravitational field itself. Eq.(A.14) keeps the left side of Eq.(A.9) invariant and is therefore often called the gauge transformation of hµν.
Plane gravitational wave and the gauge condition
We can calculate ¯hi j in any coordinate system (as long as the Lorenz condition holds) and use eqn (A.30) to convert it to theh+ and h× in the observer's coordinate system.
Gravitational wave solution I. Quadrupole radiation
This is because in these systems the tension energy of the gravitational field cannot be omitted, therefore Tµν +tµν is conserved instead of Tµν alone. Butt00 T00,ti j ~Ti j, which means (ii) is a much better approximation than (i) when calculating GW in these systems.
Gravitational wave solution II. Moving particles radiation
Stress-energy tensor for gravitational wave
Power from gravitational wave emitting
Application to Binary Systems
- Geometry of Minkovski spacetime
- Upper: The geometry of spacetime with no gravitational-wave. Lower
- The two polarization modes of the gravitational wave which propa-
- Geometry of Schwarzschild spacetime
- Spacetime of an axially symmetric stationary black hole
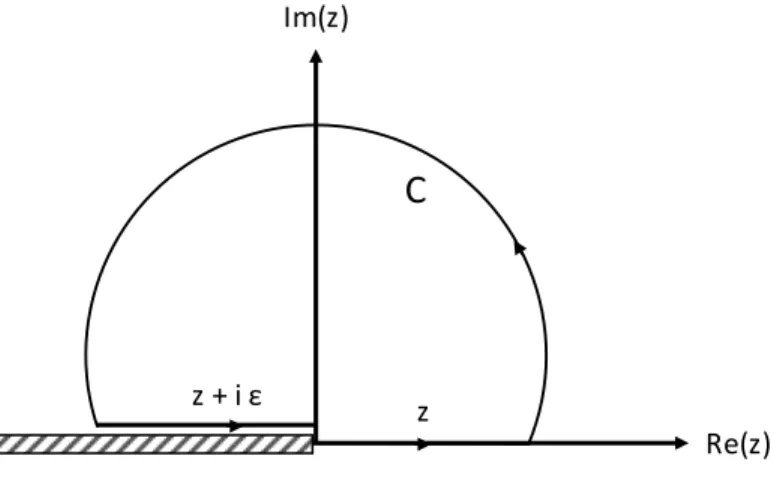
- The integration contour C in complex z plane
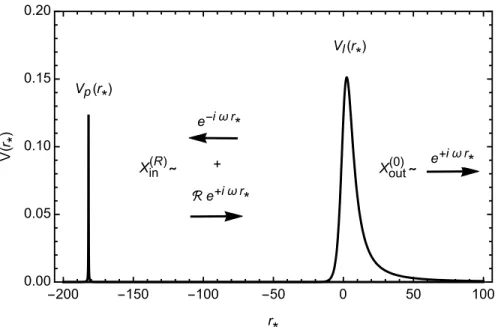
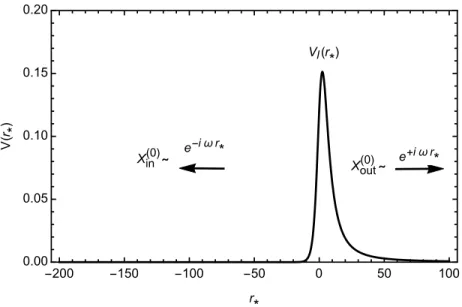
- The two homogeneous solutions X in ( 0 ) and X out ( 0 )
- The trajectory of a particle radially plunges into a Schwarzschild
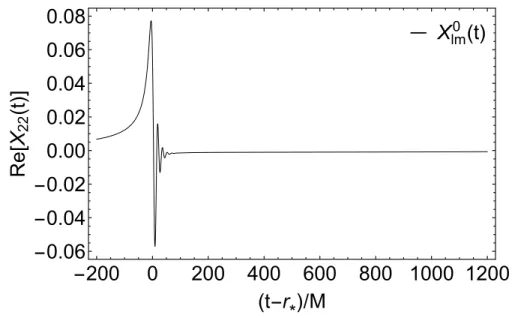
- The l, m = 2 , 2 waveform from a test particle radial plunging into a
- The l, m = 2, 2 energy spectrum from a test particle radial plunging
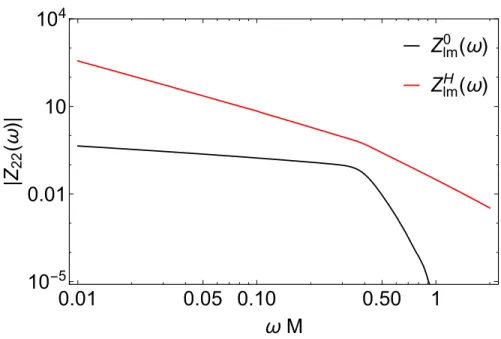
- The l, m = 2 , 2 amplitudes at null infinity and event horizon from a
- The two homogeneous solutions X in (R) and X out (R) with the Planck po-
- The spacetime plot for the main wave and echoes of gravitational-wave. 23
- The l, m = 2, 2 energy spectrum from a test particle radial plunging
- The squared changing rate of the l, m = 2, 2 waveform from a test
Comments on: "Echoes from the Abyss: Evidence for Planck-scale structure in black hole horizons". Gravitational wave signatures of compact exotic objects and horizon-scale quantum corrections.