In Chapter 3 we study the connections between properties of the action of a countable group Γ on a countable setX and the ergodic theoretical properties of the corresponding shift action of Γ↷MX, whereMis is a measure space. We also find bounds for the minimal number of generators of a dense subgroup of full groups that allow us to distinguish full groups from equivalence relations generated by free, ergodic actions of the free groupsFnandFmif mandnares sufficiently far apart.
Definable equivalence relations
Every Polish group is a continuous homomorphic image of a Polish, almost zero-dimensional (that is, at most one-dimensional) group that can be embedded as a Π03subgroup of S∞, the group of permutations of the natural numbers. Results similar to Theorem 1.1.1 were later independently obtained by Ding and Gao [11], who used a completely different method.
Countable Borel equivalence relations and orbit equivalence
Hjorth [31] showed that there are no homomorphisms countable to one from (constraints on co-zero sets of) the equivalence relation of the shift of the free group F2↷2F2 to the trajectory equivalence relation of a modular action of any group. The following theorem, a joint work by Inessa Epstein, yields a spectral property of the action that rules out the existence of such homomorphisms and is not connected to the free group, but only to receptivity.
Full groups
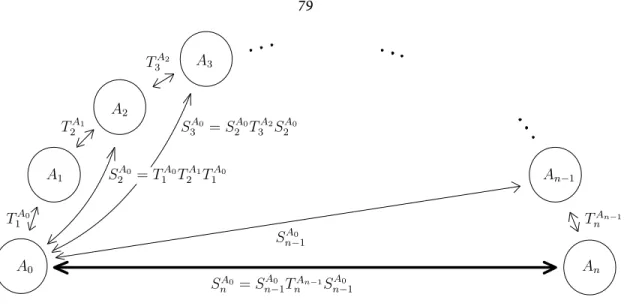
Then the following answers:. i) E can be generated by an action of a finitely generated group;. ii) [E] is topologically finitely generated. For an equivalence relation generated by a free action of Fn, we have the following explicit limits: n+1≤t([E]) ≤3n+3.
Organization of the thesis
In the last part of the paper we study polishable ideals over N and certain nearly zero-dimensional polishable subgroups of S∞ associated with them. Two examples of Polish groups are the homeomorphism groups of compact metrizable spaces with the compact-open topology, which coincides with the uniform convergence topology, and the group of permutations of the natural numbers S∞ with the pointwise convergence topology.
Compact spaces as remainders of compactifications of N
We will think of the spaceX̃as the unionX∪And we will also fix a compatible metricX.̃ Consider the homeomorphism group Homeo( ̃X). Proving and using the total limit of elements of D, if we consider i(d),d∈ Das a countable subgroup of Q, then the closure ofi(d)inQ is homeomorphic to the completion of (N,d).
Given K∈K(Q), we can find a dense countable subset of K in Borel fashion and then use the construction from the proof of Statement 2.2.1 to define a metric on N. If, on the other hand, A∉C, then any continuous extension Φ( A) switch x2kandx2k+1 to X for some k, which is impossible due to (ii).
We say that a separable metrizable zero-dimensional topology WonX witnesses the near-zero-dimensionality of (X,T )ifW ⊆ T and (X,T ) has a basis consisting of closed sets of W. Solecki pointed out that we, using a result of his, can exactly determine when the topology of a zero-dimensional Polish group witnesses the almost zero-dimensionality of a Polish subgroup.
Polishable ideals on N
Let an infinite, countable group act on a countable quantity X. i) the action of X is susceptible;. ii) the effect of Γ on MX has almost invariant sets;. iii) The Koopman representation κ0 has nearly invariant vectors. Is it true that the action has nearly invariant quantities if the corresponding Koopman representationκ0 has nearly invariant vectors.
Group actions and generalized shifts
The rest of the paper is organized as follows: in Section 3.2 we recall some necessary and sufficient conditions for a Bernoulli shift to be ergodic, mixing, etc.; in Section 3.3 we perform a detailed spectral analysis of the Koopman representation of generalized Bernoulli shifts and prove some preliminary lemmas; and finally, in Section 3.4 we give the proof of Theorem 3.1.2. Under Γ and G will always be countable, infinite groups and Q will denote a finite subset of the group. iii) the action Γ on X has infinite orbits;. Then the set {c∈MX∶c(F) ⊆A} is nontrivial and action invariant. iii) ⇒(ii) It suffices to show that the diagonal action Γ on MX×MX is ergodic. This action is the same as the Bernoulli shift corresponding to the disjoint sum of the action Γ on Xwith itself.
Recall that π is called ac0 representation if for allv∈Hπ, limγ→∞⟨π(γ) ⋅v,v⟩ =0. i) the effect ofΓ on MXis mixture;. If the action of Γ onX is not credible, then the action on MX is also not credible, so especially it is not free.
Spectral analysis of the Koopman representation
Now let T be a transversal for the action of Γ on A (ie T⊆ Aand Intersects each path in exactly one point). Note that the constant functionq0≡i0 is a path of the action of Γ on Aconsisting of a single element, soq0∈T.
Proof of Theorem 3.1.2
For more on the theory of countable Borel equivalence relations, and especially the drawable ones, see Jackson-Kechris-Louveau [34].). Kechris [41] defined the notion of an antimodular action (one whose circuit equivalence relation does not allow a count-to-one homomorphism to an equivalence relation of modular type) and isolated in the presence of an invariant measure a representation-theoretic property which implies antimodularity. Recall that if Γ acts on X-preserving a measure µ, the Koopman representation κ of Γ on the Hilbert space L2(X,µ) is the unitary representation given by .
He also asked whether the hypotheses of this theorem could be weakened, for example, if "F2 ≤ Γ" could be replaced by "Γ is not suitable" and "the action is smoothed" by "κ0 does not weakly contain a finite dimension. representation of Γ.” (If Γ is admissible, then by the well-known results of Dye and Ornstein-Weiss (see [42]), the orbit equivalence relation is hyperfinite, and therefore induced by a modular action of Z, on a set of measures 1 .) in this paper, we answer these two questions, the first positively and the second negatively (cf. Corollary 4.1.4 and Proposition 4.5.2). A unitary representation of Γ in a Hilbert space is suitable if there exists a Γ-invariant state in the C∗-algebraB(H) of bounded linear operators on H, i.e., a bounded linear functionalMonB(H) satisfying M≥0,M(I) = 1, and.
Proof of Theorem 4.1.2
However, we also require that the confluence be constant on the atoms and intersect atoms only with vertical cuts of sufficiently small size. By the assumption that θ is injective, the set of θ-examples of ⋃kBkis is dense in the gauge algebra of X×Y. Let {Bi ∣ i ∈ N} sum the atoms of Bk (if Bk contains only finitely many atoms, add empty sets to the summation).
We will show that M is a κ0-invariant state on B(L20(X)), thereby completing the proof of the theorem. Indeed, since Mi is a weak∗limit point of Mns, for everyê>0 there are infinitely many such da.
Amenable Koopman representations and almost invariant vectors
We can identify Hmetℓ2(I) and the representationπ with the representation of Γ onℓ2(I) induced by the action of Γ onI. The proof of Lemma 4.3.1 also shows that if Γ acts on a countable setI, the corresponding representation is susceptible if the action is susceptible. From the analysis of the Koopman representation of generalized Bernoulli shifts carried out in [44, Section 3], it follows that there.
LetλI be the representation of Γ on ℓ2(I), λΓdenotes the left-regular representation of Γ, and for H≤ Γ, letλΓ/H be the quasi-regular representation onℓ2(Γ/H). LetΓact on the compact Polish group G by automorphisms and let κ0 be the corresponding Koopman representation ofΓon L20(G).
Applications to orbit equivalence and Borel reducibility
Tsankov [44] that for generalized Bernoulli motions 1Γ≺ κ0 implies the existence of almost invariant sets, while it is open whether the same is true for actions on compact field groups with automorphisms. It is not known whether all inflexible groups admit a continuum of non-orbital equivalent actions. Then, if the Koopman representation κ0 corresponding to the action Γ ↷ X is irreducible, the product of the action Γ↷X×Y is µ×ν-antimodular.
It is already known that countable groups with property (T) consistently admit many such actions (Hjorth [31]). In the terminology of the proof of Theorem 4.4.2, we consider only the equivalence relations E2ΓΓandEZΓ.
A counterexample
Then for any normalized positive definite function ϕ onΓ associated with π, when 0 ≤ ak ≤ 1, ψk and θk are normalized positive definite functions onΓ, the cyclic representations corresponding to the θks do not contain π, and (1−ak ) ψk+akθk→ϕ pointwise it is always the case that ak→0. This article focuses on the study of one invariant of job equivalence, namely the full group of the job equivalence relation. Let E be a countable, measure-preserving equivalence relation on the standard probability space (X, µ) that is not an equality, e.g.
Another possible invariant (suggested by Kechris [37]) that can be looked at is the number of topological generators of [E], denoted by ([E]) (i.e., the minimum number of generators of a dense subset of [E]) . Let the equivalence relation E be created by a free, ergodic action of the free group Fn, n≥1.
Full groups are homeomorphic to ℓ 2
We will prove that the basis consisting of the open balls of the uniform metric defined by (5.1.1) has this property. Consider Sn as a simplicial complex such that all its simplexes have a ρ diameter less than δ. Since the basis of open balls is translation invariant, the following lemma suffices to verify this.
The following statements apply:. i) and (ii) are evident from the definition and properties of g. Using the above Dobrowolski–Toruńczyk theorem, it suffices to check that [E] is not locally compact.
Automatic continuity
We will repeatedly and without mentioning the simple fact that due to the ergodicity of E for all pairs of sets A,B∈MALGµ of the same measure there exists an involution T∈ [E]with T(A) =B and suppT⊆A∪B (see [42, lemma 7.10]). The following lemma and its proof are similar to Proposition 1 in the proof of [60, Theorem 12]. Now let B ⊆ B′ such that suppS ⊆ Bandµ(B) = 2µ(suppS) and note that any involution in HB can be written as a product U1U2, where U1,U2∈HB′ are involutions with µ(suppU1) = µ(suppU2) = µ(suppS).
Finally, according to Ryzhikov's argument [61], each element of HBi is the product of three involutions, thus HB⊆W36. We will show that someTm is located in W38, proving that W38 contains an open environment of 1.
Topological generators
The hyperfinite case
For the index homomorphism value we have the following simple calculation (using the fact that µ is invariant with respect to ϕ and therefore µ(Z(l,j1)) =µ(Z(l,j2)) for j1,j2 Unfortunately, little is known about topological full groups arising from non-Z group actions (especially in the non-amenable case). It is also interesting to try to find an elementary construction of a dense subgroup [E] (for a hyperfinite E) with some generators for some concrete realization of E. Matui's examples are concrete enough, but his calculations of generators rely heavily on C∗-algebraic Giordano–Putnam machines –Skau.) In this direction, Kittrell [45], using E0 (the equivalence relation on (Z/2Z)N, generated by the operation of the subgroup (Z/2Z) Let the finite equivalence relation Fn′ on B be the splitting of the orbits of ψ′ into finite pieces using the full section C (defined by a formula similar to (5.4.5)). Choose an ergodic T∈ [E/F] (like a Texist according to [37, Theorem 3.5]) and let F′ be the equivalence relation generated by T. Then there is a largest countable equivalence relation FG, such that its entire group is in G lies. Melleray, Topology of the isometry group of the Urysohn space (unpublished note available at http://www.math.uiuc.edu/∼melleray/). Nhu,The group of measure-preserving transformations of the unit interval is an absolute retreat, Proc.The general case