The themes of the conference were strongly influenced by the research developed by Gentili in the context of mathematical problems related to materials modeling. The editors are grateful to INdAM for accepting the conference proposal and general support. It is worth noting that similar conferences on mathematical models and methods for federal media were organized in Palazzono and that Gentili was one of the most active participants.
The authors of the present articles testify to their friendship and admiration for Gentili's scientific activity. In the preparation of the models, thermodynamic aspects play a central role in the characterization of the constitutive properties. He was also an effective member of the Department's Governing Council (Giunta) and often carried out onerous tasks.
First, the analysis of questions related to the relevant partial differential equations was answered through uniqueness and continuous solution dependency statements.
S. Carillo
C. Cavaterra
M. Fabrizio
Biscari* G. Caprizt
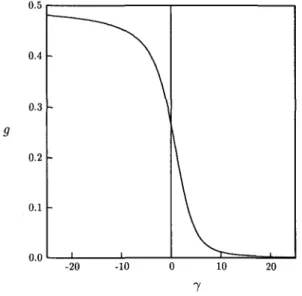
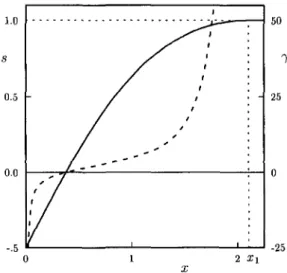
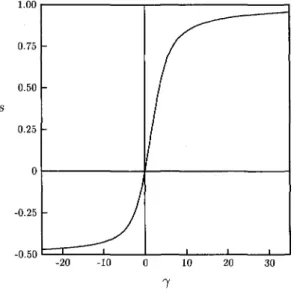
Partial order or lack thereof can be described in terms of purely geometric parameters: the degrees of prolation and of (optical) biaxiality [1]. The microscopic configuration of a single nematic molecule can be described by means of the second order tensor Qn := n ® n — | I , where n € S2 is a unit vector parallel to the molecular direction, and I is the identity tensor: thus the head-and-tail symmetry that characterizes nematic molecules is automatically enforced. 0,1] vanishes when two of the eigenvalues of Q coincide, and otherwise it is positive; s varies from — A (corresponding to the planar distribution in which all directions in the plane for the molecules are equally likely) to 1 (completely ordered distribution in which all the molecules are parallel); s and /J vanish together when and only when the order tensor is isotropic.
Q „ ) da In this case, the properties of the local order tensor Q(x), defined in (1), are determined by the nematic temper tensor B(:r), which without loss of generality can also be assumed to be traceless and symmetric, since its isotropic and oblique parts do not contribute to the scalar product in (2). In particular, the proper directions of the order tensor Q match those of the contained tensor B, as can be proved by direct calculation. To draw a parallel with classical kinetic theory, we note that B plays the role of the inverse of a temperature tensor [7].
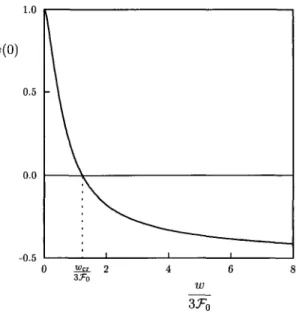
The equilibrium configuration in a nematic liquid crystal can be obtained by minimizing the functional free energy density.
Carillo *
The potential energy density due to the body-environment interaction, denoted by r and called the surface potential density [17] and [3], respectively, is assumed in the form. 4Petrovski's ellipticity [18] guarantees on 3fi the local invertibility of Sn in (9) with respect to the normal derivative of the strain. According to the definition, in particular, the first-order zero Lagrangian [17] is a functional of the form
When considering First Order Null Lagrangian [17], upon imposition of the previous conditions, it follows that the vector function w is required to depend on the position, the deformation and, in addition to the classical case, also on the first strain gradient, that is. According to the definition, in particular, a Second-order Zero Lagrangian [3] is a functional of the form. Based on the preliminary results on (P I) and (P 2), we are now in a position to state the main theorems related to the control problems formulated in the introduction.
It would be interesting to investigate this issue based on the presented results and associated techniques.
Ciarletta * S. Chiritat
Thus, in the absence of the supply terms, the fundamental system of field equations [10] consists of the stress-displacement relationship. We now proceed to establish some auxiliary identities concerning the solutions of the boundary initial value problem (V*). 3 ^ 0 and the positive definiteness of the conductivity tensor, implies that the following Poincare inequality holds.
Payne, On the backward-time stability of solutions of the Navier-Stokes equations, Arch. Our main hypothesis lies in the assumption that the vector Js is proportional to the gradient of the internal variable. Equation (19) is new and relates the superconducting current to the gradient of the internal variable via a linear law.
In light of the heat conduction theory for materials with memory (cf. e.g. and references therein), one derives equation (1) from the energy balance. Thermodynamically consistent models investigated in [6] are essentially concerned with the following form of the free energy. To obtain the equation for the evolution of the temperature, we substitute (3) into the continuity equation (1) and we get.
In the following sections we will formulate the three problems more precisely and present the relative statements of the related theorems. In particular, the condition of the points in the cross sections of the cylinder is taken into account. For this case, the frequency dependence of the spatial decomposition of the minimum free energy will be obtained.
The concept of the state of a linear viscoelastic solid has been discussed by various authors. Using symmetry arguments, this representation can be expressed as an integral over 1Z of the form It is worth noting that, based on (22) and definition 2.1, the state space E depends on the memory kernel (E characterizing the material by (10).
The main development in [27] is in terms of the history of E(, although the result (37) is also given in terms of the relative history of E*.
Hereafter we denote by G( \s\) the extension of G(s) to an even function on IR, and we assume any process P 6 II defined over all [0, oo), by means of the trivial extension . We will use the Fourier transforms of the history and continuation of the strain defined by Using the convolution theorem, Plancherel's theorem and (26), the minimum free energy can be represented in the form
In a material with fading memory, the state is usually defined using the history E*. Having verified the uniqueness of the solution of the Papapetrou-Tulczyjew equations, let us consider the case of a spin photon (polarized light). The function ip(x) is the non-convex combined free energy of the phases, the matrix.
Later we choose R so that the range of the composite map T is contained in D\. In the current summary version, evidence is omitted and so is some of the discussion. It is always possible to represent the minimal free energy as a function of the minimal state am.
The minimum free energy is therefore independent of the definition of state used. Due to the property that (Bc(w) € V(Sym), an explicit general expression can be given for the factors [2], generalization of a result derived for the scalar case in [8]. a norm in the space of the minimal states E(m).
The presentation covers the statement of the results and the basic ideas underlying the proof. A phase field system of Caginalp type (see e.g. Ch.4 in [2]) describes the evolution of the (relative) temperature •d and of the order parameter (or phase field) x m. Grasselli: Goodness of the weak formulation for the phase field model with memory, Adv.
The operator —(—A)", the fractional power of the closed linear operator —A [34], is the generator of a semigroup associated with the corresponding stable isotropic Levy process [30].
Note that cosh (a;) is a function of x2, so the square root of f < 0 in the above equation is an artifact of the definition of the cosh function. The characteristic function of the probability distribution of the Levy process Yt is {XPY, where P denotes the probability distribution of Xi and XP denotes the characteristic function of P. A Levy process {V* | * > 0} is said to be a-stable if the probability distribution P of the random variable Y\ is a-stable.
In view of the uniqueness of the IVP in question, the fundamental solutions have the following forms. The factor a/fi completely determines the scaling properties of the propagator, but for j3 < 2 the propagator has an infinite second-order moment [12]. From the above formula propagators, the propagators for d = 3 can be obtained by applying the operator (2TT r )_ 1 d/dr. iii) P( has either a single maximum or if it diverges to infinity at a single point (a priori a <5-type singularity need not be ruled out).
Given the self-similarity of the propagator, criterion (iiia) means that each radial section of the diffusion propagator Ptl represents a gradually expanding hump with a maximum or singularity at the origin. Crucial to our argument is that the second factor in the integrand (26) is unimodal with the mode at the origin for each value of the integrating variable. For the centrally symmetric operators L and 0 < a < 1, the diffusion behavior related to the unimodality of the propagator was proved.
In linear viscoelasticity, the dissipation effects due to memory lead to results of stability and decay of the energy under the hypothesis that the constitutive equations satisfy the thermodynamic restrictions (see e.g. [3]). These requests imply the convexity and exponential decay of the kernel, and using the theory of contraction semigroups or suitable estimates, a point-to-point exponential decay of the energy is obtained. In this paper, we provide a sufficient condition on the relaxation function for the exponential decay on the mean of the energy and prove that if the memory kernel has an exponential decay on the mean, i.e.
The method used here is based on the study of the Laplace transform of the solution of the evolutionary problem in linear viscoelaticity. In the linearized theory of isothermal viscoelasticity, the stress tensor T is determined by the history E' of the infinitesimal strain tensor E through the law of inheritance.