I was careful not to break the continuity and rigor of the book when I omitted topics. Some of the most beautiful mathematics has been inspired by physics (differential equations, Newtonian mechanics, differential geometry, general relativity and operator theory, quantum mechanics), and some of the most fundamental physics has been expressed in the most beautiful poetry of mathematics (mechanics in symplectic geometry and fundamental forces in Lie group theory ).
Organization and Topical Coverage
Another useful feature is the presentation of the historical framework in which men and women in mathematics and physics worked. The book concludes in a chapter that blends many of the ideas developed throughout the previous parts to address variational problems and their symmetries.
Acknowledgments
Needless to say, the ultimate responsibility for the contents of the book rests with me. Problems often fill in the missing steps as well; and in this respect they are essential to a full understanding of the book.
List of Symbols
GL(n,C) general linear group of vector spaceCn GL(n,R) general linear group of vector spaceRn SL(V) special linear group; subgroup of GL(V) with units. Sr(V) the set of symmetric tensors of type (r,0) in the vector space V Λp(V) the set of ep-forms in the vector space V.
Mathematical Preliminaries
- Sets
- Equivalence Relations
- Maps
- Metric Spaces
- Cardinality
- Mathematical Induction
- Problems
For example, in the study of the properties of integers, the set of integers, denoted Z, is the universal set. Cantor proved that 2ℵ0=c, where is the cardinal number of the continuum; that is, the set of real numbers.
Finite-Dimensional Vector Spaces
Vectors and Linear Maps
Vector Spaces
- Subspaces
- Factor Space
- Direct Sums
- Tensor Product of Vector Spaces
It is not n-dimensional real coordinate space, or Cartesian space a vector space over the complex numbers. 1 (or any pair of distinct nonzero complex numbers) are basis vectors of the vector space Cover R.
Inner Product
- Orthogonality
- The Gram-Schmidt Process
- The Schwarz Inequality
- Length of a Vector
The question of the existence of an inner product on a vector space is a deep problem in higher analysis. That this product meets all the required properties of an interior product is easily checked.
Linear Maps
Another norm defined onCnis given by ap≡. It has been proven in higher mathematical analysis that · all properties of a norm are phased. There are many applications where the preservation of the vector space structure (preservation of the linear combination) is desired.
A linear map (or transformation) from the complex vec-
- Kernel of a Linear Map
- Linear Isomorphism
- Complex Structures
- Linear Functionals
- Multilinear Maps
- Determinant of a Linear Operator
- Classical Adjoint
- Problems
For all practical purposes, two isomorphic vector spaces are different manifestations of the same vector space. It is the assertion that the only vector orthogonal to all vectors of an inner product space is the zero vector. Thenfa|bis simply the matrix14 product of the row vector (on the left) and the column vector (on the right).
Algebras
From Vector Space to Algebra
- General Properties
- Homomorphisms
Due to the isomorphism, A⊗B∼=B⊗A, we require that a⊗b=b⊗afor alla∈Aandb∈B. The last condition of the definition becomes an important requirement when we write a given algebra as the tensor product of its two subalgebras B and C. In such a case, ⊗ coincides with multiplication in A, and the condition becomes the requirement that all elements of B interchange with all elements of C, i.e., BC=CB. A subsetS⊂Ai is called the generator Aif every element of A can be expressed as a linear combination Generator of an algebra. Proposition 3.1.19 LeAandBbe algebra. Let A be a basis of linear transformation and φ:A→Ba. Then φ is an algebra homomorphism if and only if.

Ideals
- Factor Algebras
Note that there is no contradiction between this direct sum decomposition and the fact that it is central because the above direct sum is not an algebraic direct sum since L1L3= {0}. Proposition 3.2.11 If is the direct sum of algebras, then every component (or the direct sum of several components) is an ideal of A. Moreover, every other ideal of Ai is entirely contained in one of the components. Proposition 3.2.15 Let A be an algebra and B a subspace of A. Then the factorial space A/B can be transformed into a multiplication algebra.
Total Matrix Algebra
Using this and Example 2.3.22, where it was shown that φ¯ is a linear isomorphism, we conclude that φ¯ is analgebraisomorphy. Example 3.3.3 below finds that the center of Mn(F) is Span{1n}, where 1 is the identity of Mn(F). Again, due to the linear independence ofeij, for these two expressions to be equal, we must haveλjβij=λiβij for alliandj and allβij.
Derivation of an Algebra
Proof The proof by mathematical induction is very similar to the proof of the binomial theorem of Example 1.5.2. As in the case of the derivation, one can show that keris is a subalgebra of A,(e)=0 ifA has an identity, and is entirely determined by its action on the generators of A. A Particular example of the second case is when an antiderivation with respect to an involution ω is such that ω= −ω.
Decomposition of Algebras
- The Radical
- Semi-simple Algebras
Note that since some of the a's may be inL, the index of LA is at most equal to the index of L. Furthermore, it is not difficult to show that the only vector common to two of the summands is the zero vector. If one of the two, e.g. Q, is not primitive, write it as Q=P2+P3, with P2 and P3 orthogonal.
An algebra whose radical is zero is called semi- simple
- Classification of Simple Algebras
- Polynomial Algebra
- Problems
We conclude our discussion of the decomposition of an algebra with a further characterization of a simple algebra and the connection between primitive idempotents and minimal left ideals. Proof Since a semi-simple algebra is a direct sum of simple algebras each independent of the others, without loss of generality, we can assume that A is simple. For any fixed elementa∈A, consider the setP[a] of elements in the algebra of the form.
Operator Algebra
Algebra of End( V )
- Polynomials of Operators
- Functions of Operators
- Commutators
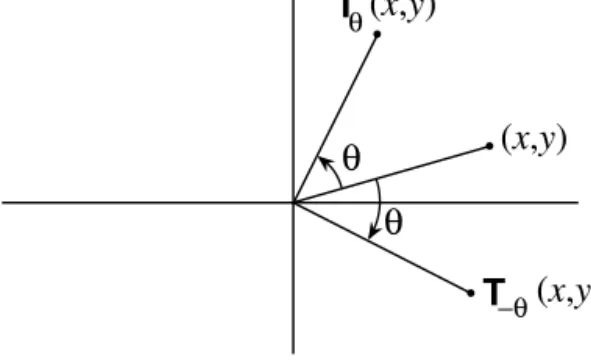
Comparing this with the action of Tθ in the previous example, we discover that the only difference between the two operators is the sign of the sinθ term. We can go one step beyond polynomials of operators and, via Taylor expansion, define functions of them. The reader will recognize the final expression as a rotation in the xy plane generator of the rotation.
Derivatives of Operators
In fact, it can be shown that many operators of physical interest can be written as a product of simpler operators, each of the form exp(αT). As long as we keep track of the order, virtually all differentiation rules apply to operators. Sometimes this is written symbolically as etABe−tA=. where the RHS is simply a truncation of the infinite sum in the middle.
Conjugation of Operators
- Hermitian Operators
- Unitary Operators
What is the analogy of the well-known fact that a complex number is the sum of a real number and a purely imaginary number. Example 4.3.8 In this example, we illustrate the result of the above theorem with 2×2 matrices. From the discussion of the above example, we conclude that the square of the invertible Hermitian operator is positive definite.
Idempotents
- Projection Operators
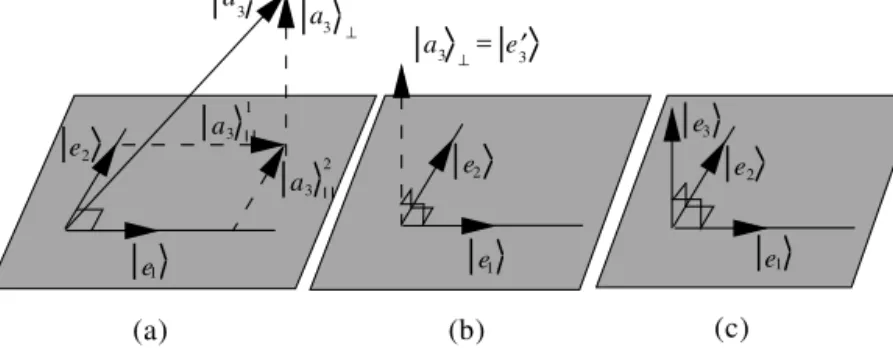
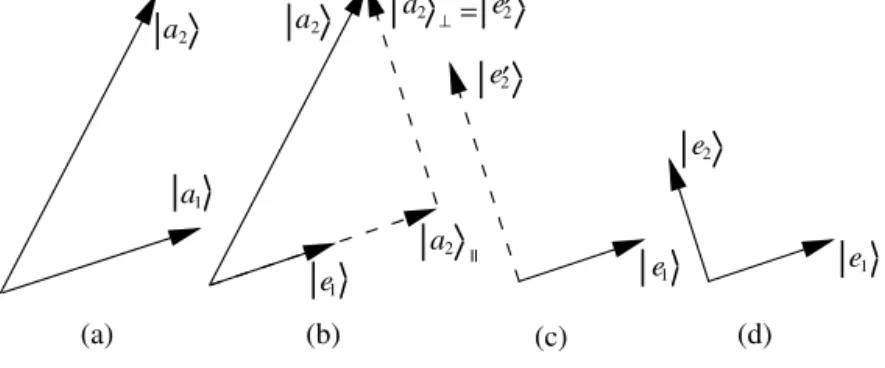
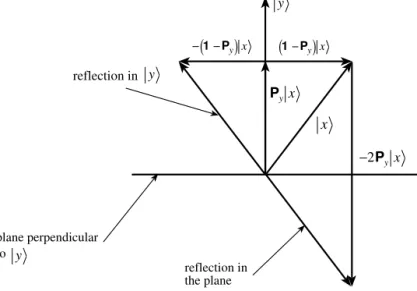
12One can notice more directly—also shown in Fig.4.2—that in three-dimensional geometry, if one adds|xtwice the negative of its projection onto|y, one gets the reflection of|xin perpendicular to the plane |y . For any other vector|x, the component|xyof|xalong|y and its reflection|xr,yin the plane perpendicular to|y is given by. Example 4.4.8 We want to find the most common projection and reflection operators in a real two-dimensional vector spaceV.
Representation of Algebras
If the productη1η2 is negative, we can define a new angle which is the negative of the old angle. Since an algebra is also a vector space, it is possible to reach it using certain |aandain. Thus|a ∈Awwhen the member is considered as a vector anda∈Awwhen the same member is one of the factors in a product.
Problems
We have shown that if two irreducible representations of a semisimple algebra have the same kernel, then they are equivalent. Show that P(m) projects onto the subspace spanned by the firstmvectors in B. Hint: Find a unit vector in the direction of the line and construct its projection operator. For the "only if" part of an irreducible representation, take|v to exist in every subspace of V.
Matrices
Representing Vectors and Operators
Box 5.1.1 To find the matrix A that represents A in bases BV = {|ai}Ni=1andBW= {|bj}Mj=1, printA|aias a linear combination of the vectors inBW. The components form the first column of A. Example 5.1.3 In this example we construct a matrix representation of the matrix representation of the complex structureJ complex structureJoin a real vector spaceVIntroduced in Sect.2.4. As long as all vectors are represented by columns whose entries are expansion coefficients of the vectors in B, A and A are indistinguishable.
Operations on Matrices
The elements of a symmetric matrixA satisfy the relationαj i=(At)ij= (A)ij=αij; i.e. the matrix is symmetric under reflection through the main diagonal. The denkth column of a Hermitian matrix is the complex conjugate of its kth row, and vice versa. In words, the function of a diagonal matrix is equal to a diagonal matrix whose entries are the same function of the corresponding entries in the original matrix.
Orthonormal Bases
Box 5.3.1 Only in an orthonormal basis is the adjoint of an operator represented by the adjoint of the matrix representing that operator. Example 5.3.2 Consider the matrix representation of the Hermitian operatorHin a general—not orthonormal—basisB= {|ai}Ni=1. This equation gives the first half of the requirement for a unit matrix given in Definition 5.2.4.
Change of Basis
This equation has a corresponding matrix equation b=Aa. Now, if we change the base, the columns of the components|ain|b will change to those of a′inb′. Box 5.4.1 To find the ijth matrix element that changes the components of a vector in the orthonormal basis B to those in the orthonormal basis B', take the jth ket in B and multiply it by the ith bra in B'. To find the ijth element of the matrix that changes B′vB, we take the jth ket in B′ and multiply it by the ith bra inB:ρij′ = ei|e′j.
Determinant of a Matrix
- Matrix of the Classical Adjoint
- Inverse of a Matrix
Since by Corollary 2.6.13, the classical adjoint of Ai is essentially the inverse of A, we expect its matrix representation to be essentially the inverse of the matrix of A. Equation (5.26) shows that the classical adjoint matrix is the transpose of of the cofactor. We have also related this intrinsic property to the determinant of the matrix representing that operator in some basis.
A matrix is in triangular, or row-echelon, form if it satis-triangular, or
- Dual Determinant Function
- The Trace
- Problems
Theorem 5.5.11 The rank of a matrix is the dimension of the largest (square) submatrix whose determinant is not zero. The shape of the choices is dictated by the assumption that the first entry of the matrix reduces to 1 when θ=0. Now expand the determinant of the new matrix by its sixth row (column) to show that.
Spectral Decomposition
Invariant Subspaces
It is easy to show that 1−P is a projection operator that projects onto M⊥ (see Problem 6.1). We have seen several times the importance of the Hermitian conjugate of an operator (e.g. in connection with Hermitian and unitary operators). Let us now investigate some properties of the adjoint operator in the context of invariant subspaces.
Eigenvalues and Eigenvectors
Theorem 6.2.2 Add the null vector to the set of all eigenvectors of A that belong to the same eigenvalueλ, and denote the span of the resulting set by Mλ. Then Mλ is a subspace of V, and every (non-zero) vector in Mλ is an eigenvector of A with eigenvalueλ. By their own construction, eigenspaces corresponding to different eigen-. values have no vectors in common except the zero vector. This equation says that |a is an eigenvector of Aif and belongs to the kernel of A−λ1 only if |a.
![Fig. 1.3 The union of all the intervals on the x-axis marked by heavy line segments is sin −1 [ 0, 1 2 ]](https://thumb-ap.123doks.com/thumbv2/123dok/10247436.0/35.786.108.535.105.273/fig-union-intervals-axis-marked-heavy-line-segments.webp)