The main dynamic characteristics of tall buildings are within the shear beam model. The coupling of translational and rotational vibrations in modes is similar to other types of coupled vibrations, for example . vibrations of buildings with light towers or offsets that have been discussed in the literature. C9,10). The purpose of this study is to evaluate the effect of modal coupling on the earthquake response of tall buildings.
DYNAMIC MODELS OF TALL BUILDINGS Introduction
The preceding assumptions lead to a mathematical model that is a three-dimensional generalization of the well-known slider. Due to the assumptions that only movements take place in the horizontal plane and that the floors are rigid,. The vertical z-axis locates the centroid of the complete structure and r is defined as the radius of the tower of the structure around the z-axis.
CONTINUOUS MODEL
DYNAMIC PROPERTIES OF TALL BUILDINGS Introduction
-21) However, from (3-19) mode forms of the same type differ only by a scaling function of z as the equation. The other mode shapes are arbitrary, orthogonal combinations of the other two components of x(z), r6(z). One of the properties of [F(z)] is that the off-diagonal terms, xf(z) and yf(z), only directly couple translational and torsional motions.
BUILDING MODEL
LEGEND
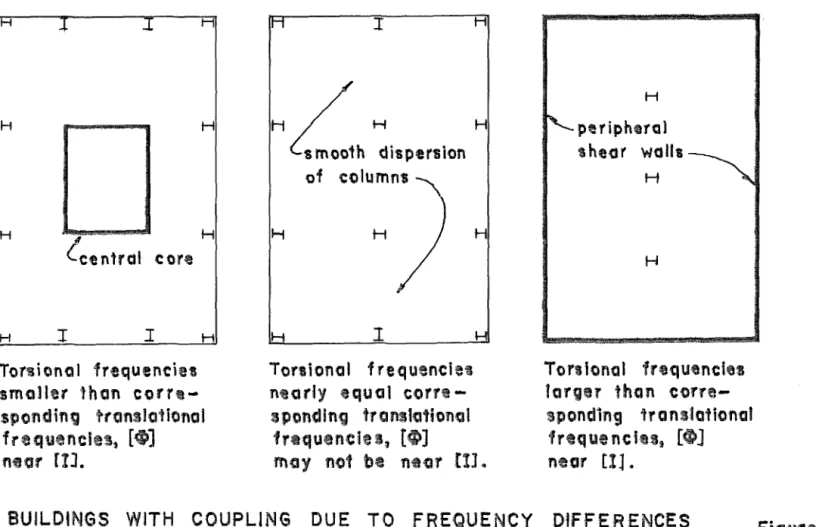
Due to the fact that the first two columns [¢] can be interchanged or multiplied by minus one, it is always possible to let the angle S be less than or equal to TI/4 in absolute value. From Figure 14 and the equations above, it can be seen that [¢] is close to [I] if and only if the eccentricity ratio is small relative to the fractional frequency difference. This chapter shows that there is a constant matrix of modal components [¢] for tall buildings with certain typical properties.
Sufficient building properties for [¢] = constant are non-eccentric symmetry or constant eccentricity and stiffness ratios. When the translational and torsional stiffness are well separated and the eccentricities are small, such as in a rectangular building.
MOHR'S CIRCLE
APPLICATION OF PERTURBATION THEORY Introduction
Extending the results of Chapter I I I to include a mass distribution which varies with z, it is seen that the mode shapes and natural frequencies are given by the solutions of Eq. The zero-order equation of the previous section, equation (4-8)' which would be correct in the undisturbed case, can be. The first summation term in this equation is a sum of vanishing differential equations of the form given by equation (4-11).
Moreover, if p is equal to i, the coefficient of the integral reduces to Aik' and thus the first-order correction to the natural frequencies vanishes, that is. Equation (4-20) states that the first-order correction to the mode shape in terms of the principal component of the mode shape is just a scaling multiple of the principal component. Therefore, since only the relative values of the first-order modal components are of interest, this scaling multiple can be taken equal to zero.
These relations provide the convenient simplification that the first-order correction to a mode shape has no component in the direction of the principal component of that mode shape. In the case for which [¢] is equal to [I], the principal components of the mode shapes are simply x, y, or rotational, and the k and j values of 1 and 3 correspond to translational directions. Therefore, if the principal components of the mode shapes are simply x, y, or rotational, the first-order contribution in one translational direction to a mode shape whose principal component is in the other translational direction is zero, unless a certain pair natural frequencies. are equal; so the equation.
In this chapter, the constant matrix [¢]p is determined as representing the nearly constant ratios of modal components.
THE EFFECT OF EARTHQUAKES ON TALL BUILDINGS
The symbols used in this chapter are defined below and wherever possible symbols from previous chapters are used. The decoupling, in this convenient way, is a consequence of the existence of a constant orthogonal matrix of modal components. Incorporating these assumptions into equation (5-9) with p replaced by i, and incorporating the simplified ground motion estimate, it can be shown that.
In terms of the velocity spectrum value ' suitable for each mode, the maximum value of nik(t) and its derivatives is found to be. 5-12) It is important to combine the response in the different modes to determine the relative displacements, relative velocities and absolute accelerations of the structure. As a further complication, when one of the components dominates the other, the difference becomes apparent. From discussions in Chapter III it is seen that for many applications at least two of the i-mode natural frequencies will be close to each other if [¢] is not close to [I] and the eccentricities are small.
Blinking can occur between all three i-th eigenfrequencies, but this seems unlikely. This estimate is an upper bound on the desired root-mean-square combination of the absolute sum of the two largest components with a third component and is a useful estimate in the case of interest for which modal coupling is strong. To aid in the comparative study of the effect of modal coupling, the index u will be used exclusively for all values for which.
From equations (5-17) and (5-18) it is possible to determine the maximum relative displacements and absolute accelerations at the center of mass of the building, as well as the maximum rotations and rotational accelerations.
APPLICATION TO THE SAN DIEGO GAS AND ELECTRIC BUILDING Introduction
A photograph of the building is shown in Figure 17, while Figure 18 shows a typical floor plan of the building. The mode shapes thus determined can be displayed as shown in Figure 19, which shows the motion of the twentieth floor vibrating in each of the basic mode shapes. The graphs of the three components of the fundamental mode shapes shown in Figures 20 and 21 show that the x, re, and y motions are in nearly the same ratio for the entire height of the building.
The vectors of the matrices [¢] and [¢] are drawn in x (South) r8 (rotation from South to East) y (East) space as shown in figure. The plotted mode shapes for the three fundamental modes are almost of the same shape, approximately a straight line as seen in figures 20 and 21. -11) Based on the assumption that the center of mass and the center of area coincide, the approximate location of the center of stiffness is shown in figure 18.
From equation (3-5) which follows directly from the equations of motion for the continuous model it is seen that the upper right and lower left corner elements of [F(z)] are zero. 6-8) these elements are small, indicating that the matrix [¢] is chosen to represent the mode shapes of San Diego Gas and Electric. Due to the fact that the fundamental frequencies and hence the diagonal elements of [F (z)] for the San Diego Gas and Electric Building are labeled in increasing order of magnitude, and due to the fact that F. 3 as well as the second and third lines of [¢] as determined by rough analysis are swapped. As such, without knowing the experimentally determined value for [¢], one can conclude that the first and third columns of [¢]A or [~]AN are satisfactory.
The estimated earthquake response of the San Diego Gas and Electric Building, in terms of relative displacements, etc., can be determined using the results of Chapter V.
MODE I
FUNDAMENTAL MODES FROM PERTURBATION THEORY
Shear stresses are expressed in the same units as the average soil weight W divided by the area A. As an upper limit based on the assumption that there is strong modal coupling, the maximum responses that would occur for any [¢] are calculated. also. Three response determination schemes can then be compared, only the first of which depends on the exact fundamental modal set in the building.
Figure 24 shows that the estimated seismic response of the San Diego Gas and Electric building is much larger than would be expected if the mode shapes are assumed to be uncoupled. Indeed, if the resistance is uniformly distributed over the floor area, as is the case for this building, the 5% random eccentricity prescribed by the Uniform Building Code is <24.
Ayre, R.S., "Interconnection of Translational and Torsional Vibrations in Buildings," Bulletin of the Seismological Society .Qi America, (april, 1938). Ayre, R.S., "Experimental Response of an Asymmetric, One-Story Building Model to an Idealized Transient Ground Motion," Bulletin of the Seismological Society of America, (april, 1943) s. Medearis, K., "Coupled Bending and Torsional Oscillations of a Modern Skyscraper," Bulletin of the Seismological Society of America, (august, 1966), s.
Newmark, N.M., "Torsion in Symmetrical Buildings, 1'1 Proceedings of the Fourth World Conference on Earthquake Engineering, Vol. Housner, G.W., and Outinen, H., "The Effect of Torsional Oscillations on Earthquake Stresses, "The Effect of Torsional Oscillations on Earthquake Stresses, Vol. Oscillations on Earthquake Stresses," Bulletin of the Seismological Society of America, (July, 1958), p of Technology, Pasadena, CA, (1970).
Trifunac, M.D., "Ambient Vibration Test of a Thirty-Nine Story Steel Frame Building," Earthquake Engineering Research Laboratory, California Institute of Technology, Pasadena, Kalifornië, (Julie, 1970). Blume, J.A., "Period Determinations and Other Earthquake Studies of a Fifteen-Story Building," Proceedings of the World Conference on Earthquake Engineering, Berkeley, Kalifornië, (Junie, 1956), pp. Housner, G.W., "Behavior of Structures during Earthquakes" , Tydskrif van die Afdeling Ingenieursmeganika, ASCE, (Oktober, 1959), pp.
Hudson, D.E., "Synchronized Vibration Generators for Dynamic Tests on Full-Scale Structures," Earthquake Engineering Research Laboratory, California Institute of Technology, Pasadena, Californien (november, 1962).
APPENDIX I
APPENDIX II
If any of the equations (II-5) through (II-7) involve a division by zero for all z and z, the corresponding equation in. II-2) to (II-4) is identically satisfied, and the resulting restriction on [ F(z)] is of no further consequence.
APPENDIX III