Also, I would like to express my gratitude to every person with whom I had the good fortune to interact during my doctoral studies. At the risk of forgetting many names, I would like to particularly acknowledge the contribution of a few key individuals.
The Setup
The suboptimality of the point-to-point approach is also well established for general multi-user channels (see [7, 8]) and transmission over networks with more than one source-destination pair (see [9]). This further highlights the inadequacy of point-to-point approach when dealing with multi-terminal data compression scenarios.
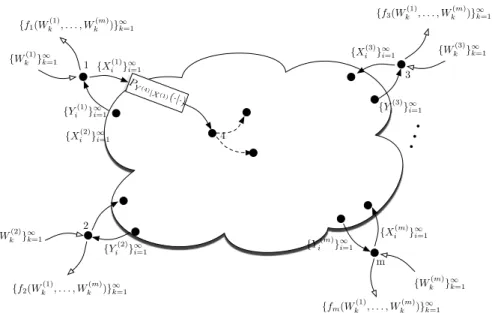
Our contribution
Network Reduction
Combined with the results of [10] and [11], these results allow us to focus our attention exclusively on networks of lossless connections when the networks consist of point-to-point channels. Following the results from this chapter, the remainder of the dissertation focuses exclusively on networks of error-free links.
Feedback in Network Source Coding
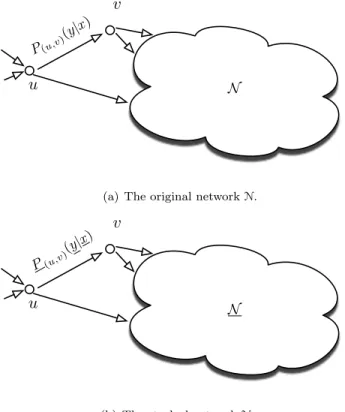
The approach discussed in Chapter 2 shows that finding the adversarial coding capacity of a network of point-to-point independent noisy channels is equivalent to finding the adversarial coding capacity of another network consisting exclusively of error-free links with known capacity. In Section 2, we formally express this notion and show that while this equivalence holds for some resource collections, it fails for general data compression problems.
Side Information in Networks
Thus, it is asymptotically optimal to allow the adversarial network code to operate independently of the channel code in this framework. In section 2.3 we show that the adversarial capacity of a network is the same as that of a stacked network consisting of many copies of the same network.
Preliminaries
Network model
In Section 2.4, we show that replacing one of the channels with a noiseless link of equal capacity does not change the adversarial network coding capacity of the stacked network. Consequently, the feasibility of a given collection of demands over a given network may depend critically on the joint distribution of the resources present.
Network code
We assume that each transmission on edge e involves a delay of unit time and that the noise on all channels is independent and memoryless. Without loss of generality, we assume that all messages are either binary vectors or binary matrices of appropriate dimensions.
Adversarial model
Stacked network
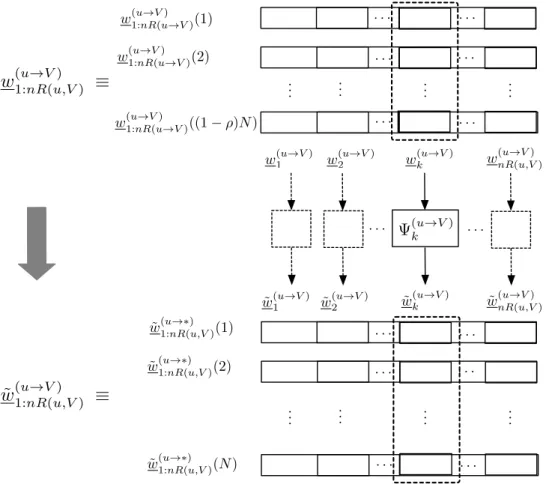
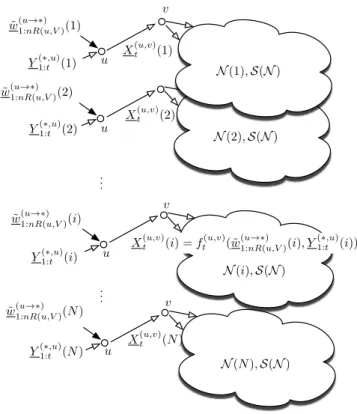
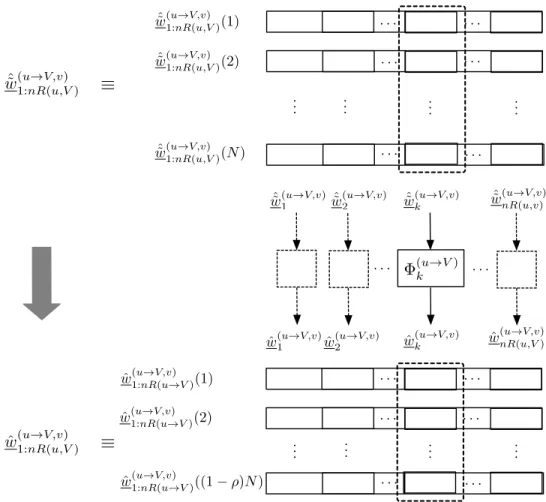
We then send each row of the resulting binary matrices( ˜w(u→V1:nR(u,V) ): (u, V)∈ M) on a different layer using the solutionS(N). Let wH(·) denote the number of 1's in a binary vector. a) The time-transmitted vector uin the ith layer to time step.
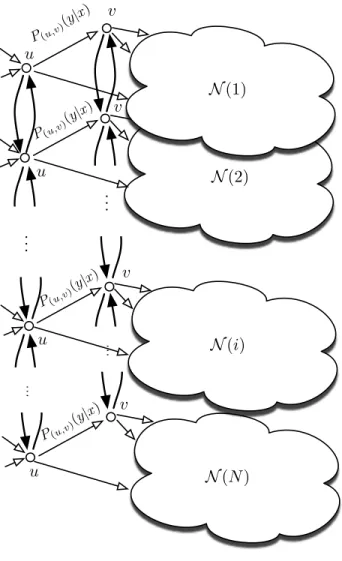
Network equivalence
To accommodate this possibility, we modify the proof of [10] to use a universal source code that first determines the type of the received sequence and then emulates the channel using a source code designed specifically for the observed type. Finally, we conclude that the error probability of the solution Sˆ(NR) vanishes as N grows without bound.
Equivalence for network source coding
Multicast Demands with Side Information at Sinks
The proof follows directly from the fact that those rate regions for both 1 and 2 are fully characterized in terms of their respective source entropies.
Networks with independent sources
An example where equivalence does not apply
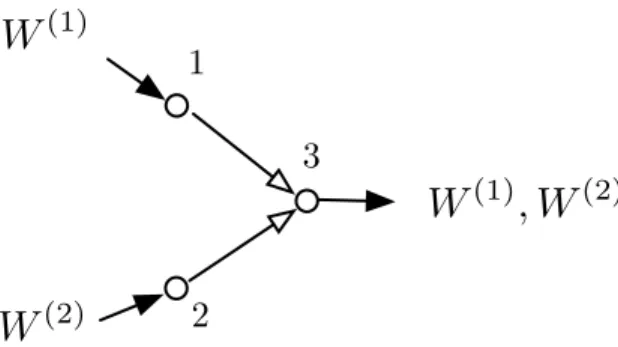
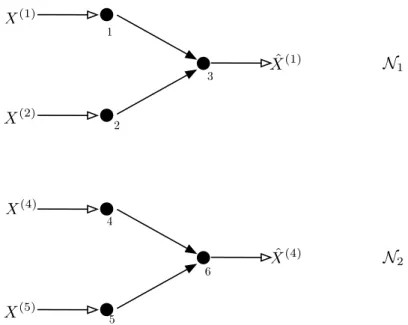
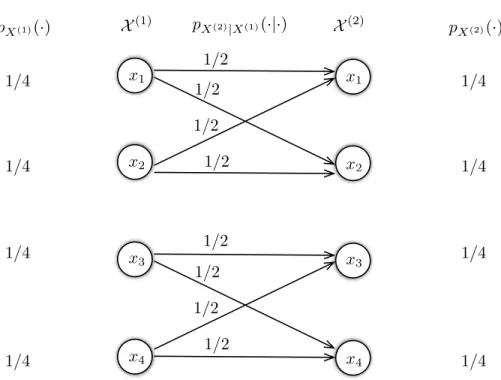
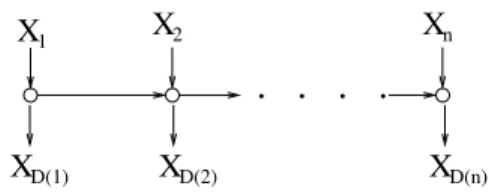
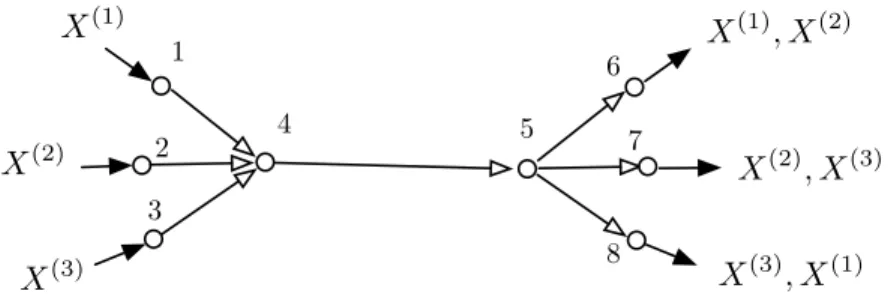
Consider network N1 consisting of the sources W(1) and W(2) observed at vertices 1 and 2, respectively, and lossless demand W(1) at vertex 3. Similarly, network N2 consists of the sources W(4) and W( 5) observed at vertices 4 and 5, respectively, and claim W(4) at vertex 6. Given an n-node line network N (shown in Figure 3.1) with memoryless sources X1, X2,. provided that one of the following conditions applies:. n}, receiver i demands a subset of the sources X1,.
Unfortunately, in some cases the given decomposition fails to capture all the information known at previous nodes, and so the feasibility result given by the additive construction is generally not tight.
Preliminaries
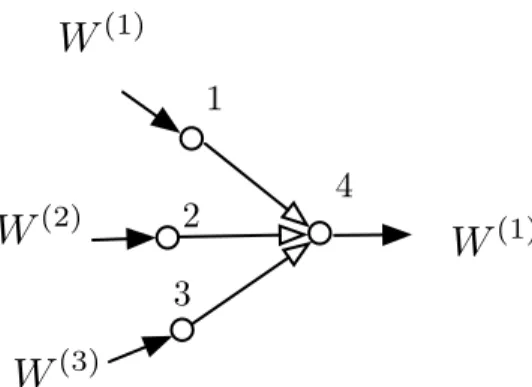
The failure of additivity in this case arises from the fact that, for a given functional source coding problem, the component decomposition of the network does not capture other information that intermediate nodes can learn beyond their explicit requirements. The same problem can also be replicated in a 4-node network where all resources (including the one previously described as a function) are available on the network.
Results
- Cutset bounds and line networks
- Independent sources, arbitrary demands
- Dependent sources, multicast
- A special class of dependent sources with dependent demands
- Networks where additivity does not hold
This shows that the rate assignment for N can also be obtained by summing the rate assignments for the component networks over links. In particular, for the system shown in Figure 4.2, Slepian and Wolf [6] showed that the minimum velocity required at the forward link is equal to the cutting limit. Since the addition of feedback does not change the cutting edge, it follows that the required rate cannot be reduced.
When setting zero error, the cutting limit is not achievable for the system shown in the figure.
Preliminaries
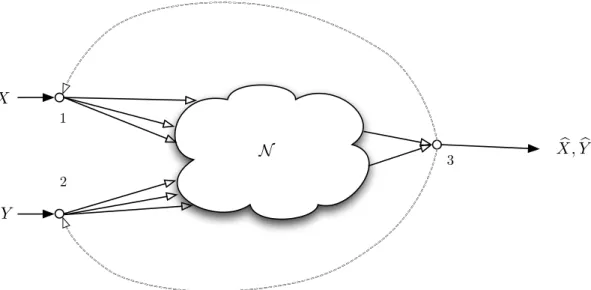
The achievable rate region indicates the set of rate vectors for which there exist sequences of codes that satisfy a desired decoding criterion. The sink t demands the pair (X,Y) with an error probability that vanishes asymptotically with the dimension of the code. For each of the above decoding criteria, the reachable rate range with feedback is defined as the set of rate vectors R ∈ RE that are reachable on N under the given decoding criterion and is usually denoted by R(N).
The achievable free-feedback velocity range RF(N) is defined as the set of velocity vectors R∈ RE\F that are achievable at NF under the given decoding criterion.
The role of feedback in source coding networks
Source coding with coded side information
- Networks with multicast demands
Furthermore, we also show that the ratio between the required rates on a given forward link with feedback and the required rate on the same link without feedback can be arbitrarily small when we fix the rates on the other link. Similarly, let C2⊆V be the cut containing vertex2 that achieves the minimum cut velocity M( ˆR,{2},{t}) for the velocity vectorR. The speed range for this network, both with and without feedback, is given by the set bounds, as shown in [18].
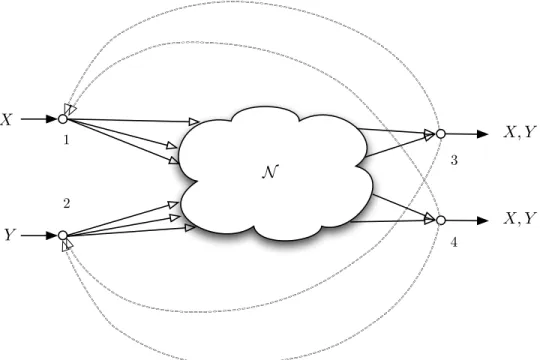
SourceX is observed at node1 and sourceY is present at node2 as side information. The decoder requires a lossy reconstruction of Xˆ X subject to the distortion criterion Ed(X,X)ˆ ≤ D.
Achievable rates for multi-terminal lossy source coding with feedback
Further, since dX and dY are finite distortion measures, to show that the expected distortion of this code can be made arbitrarily close to (DX, DY), it suffices to show that Pr(1ndX(X, f (ˆUn,Vˆn) )> DX+δ)and Pr(n1dY(Y, g(ˆUn,Vˆn))> DX+δ)can be made arbitrarily small for any δ >0. From the AEP, the probability of this event can be made arbitrarily small by choosing a sufficiently large size. Following a similar reasoning as above, as long as R013 > I(X, V;U), the probability of this event can be made arbitrarily small.
Also, the probability of this event can be made arbitrarily small by choosing n large enough, the number of elements in each bin is less than 2nI(U;V), with the probability approaching 1 growing without limit.
Finite feedback
Upper and lower bounds
- Upper bound
- Lower bound
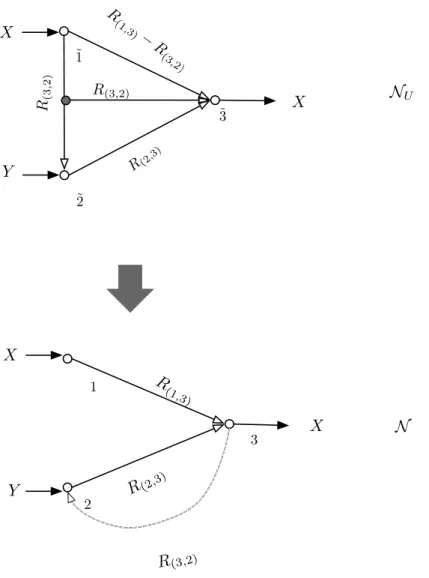
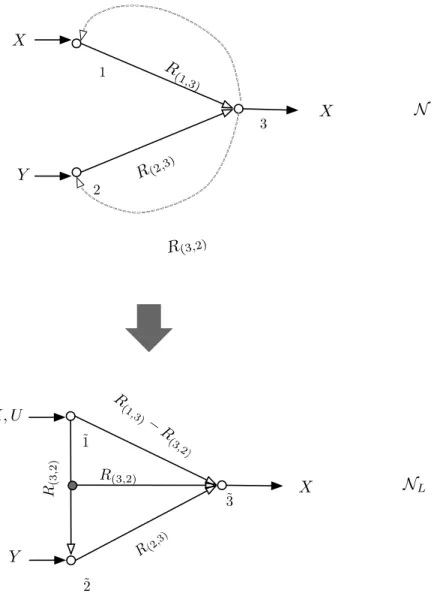
Similar to the result in previous section, we find a lower bound for the rates required for the network of Figure 4.4 by comparing it with the network shown in Figure 4.10.
Zero-error source coding
Since the mapping from x to the pair (B(x), IB(x)(x)) is one-to-one, the above protocol ends up decoding Eyx correctly for every x∈ Xn. Let Rn(1,2) and Rn(2,1) denote the expected rates in the forward link and the backward link. The converse follows immediately from the Slepian-Wolf problem since the rate required in the forward link for zero-error coding is not less than the rate required for the asymptotic lossless Slepian-Wolf code.
Finally, using the same argument as in Theorem 13, as long as R > H(X|Y), the expected forward link velocity for the above code approaches R as n grows indefinitely, while the reverse link velocity approaches 0.
Discussion
In this chapter, we investigate the range of network source coding rates for multisource networks with multicast requirements in the presence of side information. For the case where the side information is present only at the terminal nodes, we show that the rate range is precisely defined by the cut boundaries and that random linear coding is sufficient to achieve optimal performance. 18] proved that cut-set bounds are narrow for multicast codes on dependent sources and that linear codes are sufficient to achieve optimal performance.
We consider several generalizations of this simple model that include side information random variables that are jointly distributed with the source random variables.
Preliminaries
- Network model
- Sources and sinks
- Demand models
- Multicast with side information at the sinks
- Multicast with side information at a non-sink node
- General demands
- Network source codes
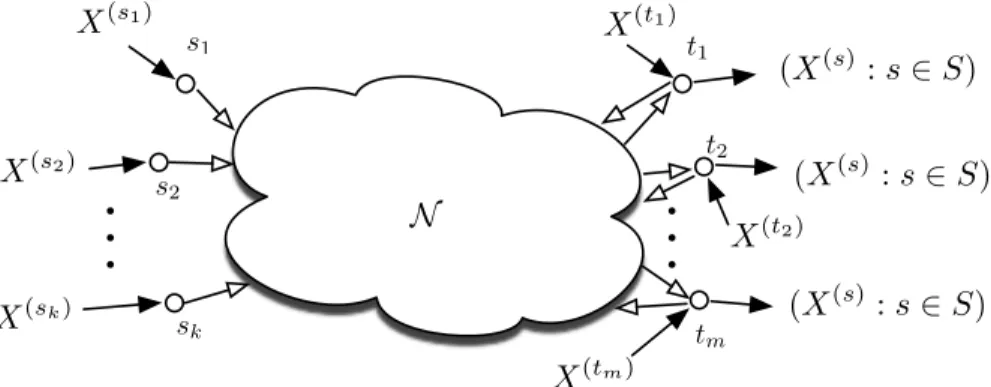
We say that the Nhasmulticast network requires side information at the sinks (Figure 5.2) ifSt=S for all t ∈T and X(v) = 0 for all v /∈ S∪T. So each sink requires all resources (X(s):s∈T); the side information may differ per sink. So each sink requires all resources(X(s):s∈T); the side information may differ per sink.
Here we put no restriction on the set of sources required at each sink (Figure 5.10).
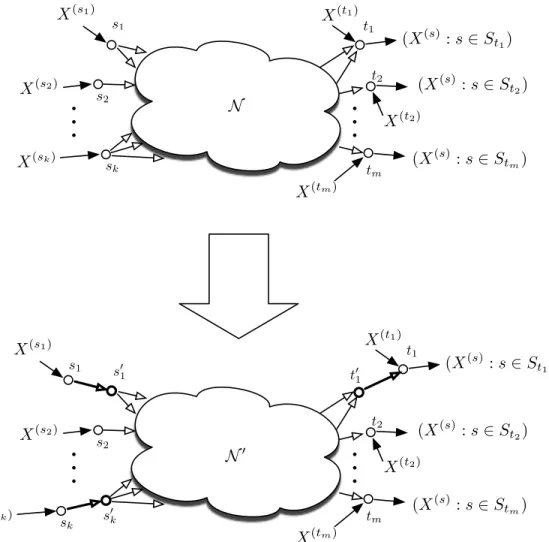
Multicast with side information at the sinks
Achievability via random binning
Thus, the above result does not imply reaching the norm region through random connection. Define the network Nrme has the same set of vertices and edges as N and sources(X(s):s∈S) replaced by(B(s)(X1:r(s)) :s∈S), where each B(s)( · )is a random concatenation operation with rateRs+. From the proof used in the reachability result in [9] for the case of multicast with independent sources, the error probability for random link codes in N˜ approaches zero asymptotically.
To determine the error probability for a code formed by random binning approximations0, consider any series of codes {(˜F(n),G˜(n))}that are valid for the networkN˜r.
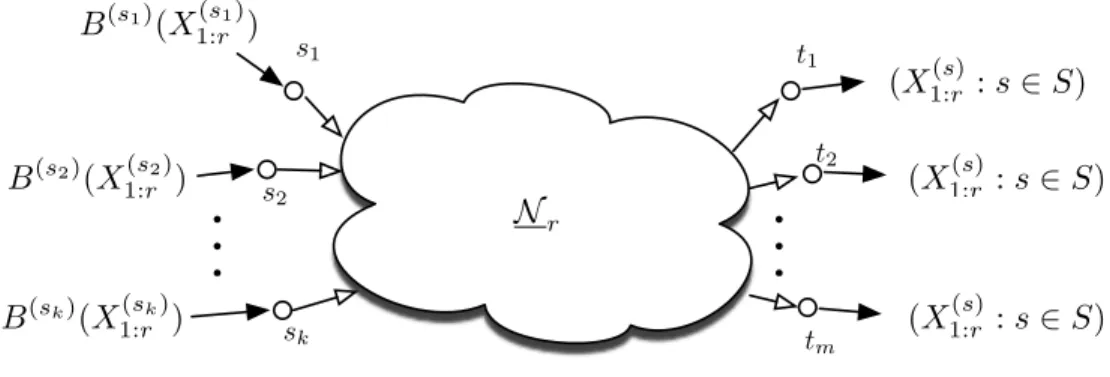
Multicast with side information at a non-sink node
We use an approach similar to that used in the coded side information problem of [29]. Now, using an argument similar to the one that allows us to obtain the region given by (5.3) from that given by (5.2) in Theorem 16, the upper region is equal to the set of rate assignments Rτ that satisfy. When there is exactly one sink node1 and one source node1, the region described in Theorem 19 reduces to the set of vectors R that satisfy.
In contrast to the Source Coding Theorem [29], it follows that the upper region is tight if no directed path from s1tot1 has a common edge with a directed path from odz to tot1.
An inner bound on the rate region with general demand structures
This shows that the conditions of Theorem 19 are not necessary for the degree vector to be attainable. According to Theorem 16, the rate vector R(σ,k) is sufficient to meet the requirements of the k-th multicast session if the following condition is satisfied:. 5.11) Adding the rates required for each multicast session gives the reachability of the region Rσ. While the closed-form expression for the upper velocity range may be difficult to analyze, it is algorithmically easy to calculate.
However, it should be noted that the above tariff region is generally not tight.
Discussion
Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. Universal multiterminal source coding algorithms with asymptotic zero feedback: Fixed database case.Information Theory, IEEE Transactions on dec. Wyner-ziv theory for a general function of correlated sources.IEEE Transactions on Information Theory, IT September 1982.