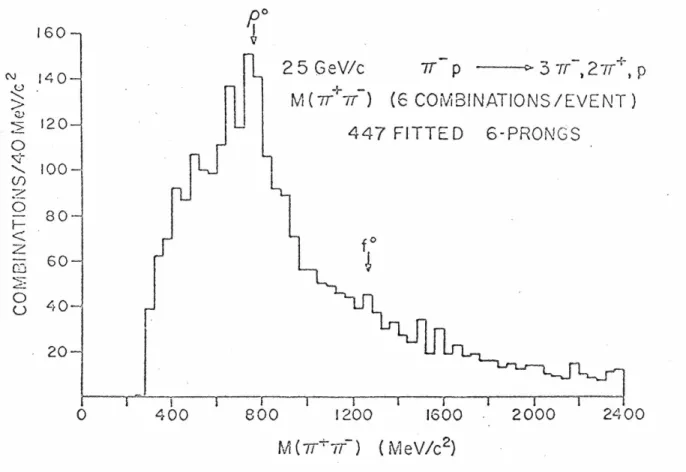
It is concluded that the effects of the many possible correlations may be difficult to resolve in the current analysis of existing data. The energy dependence of the cross section for the production of the I = 3/2 component in our example. The Pomeron is assigned the quantum numbers of the vacuum to ensure its exchange in elastic scattering and diffraction dissociation.
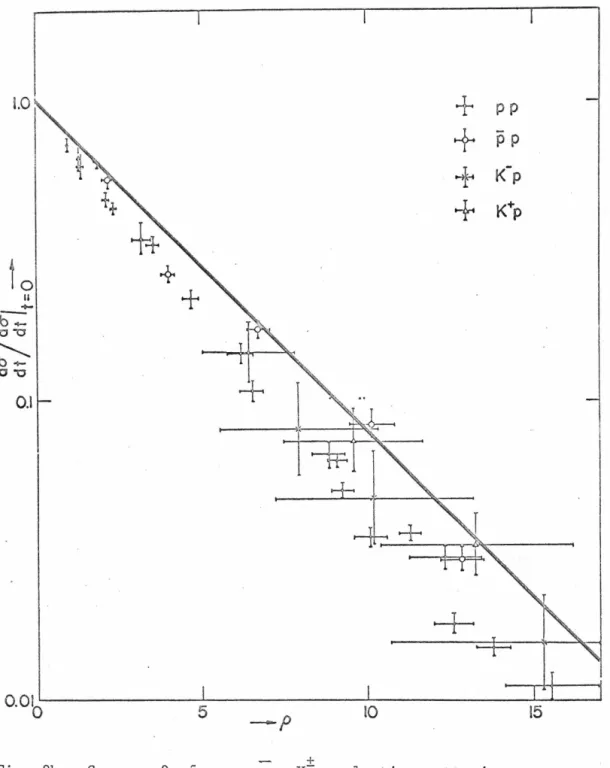
The value of the intercept implies that an amplitude dominated by pion exchange is predominantly real. Via the optical theorem, this cross section is proportional to the imaginary part of the forward scattering amplitude. Our aim in this section is to derive the general angular distributions for reactions of the type.
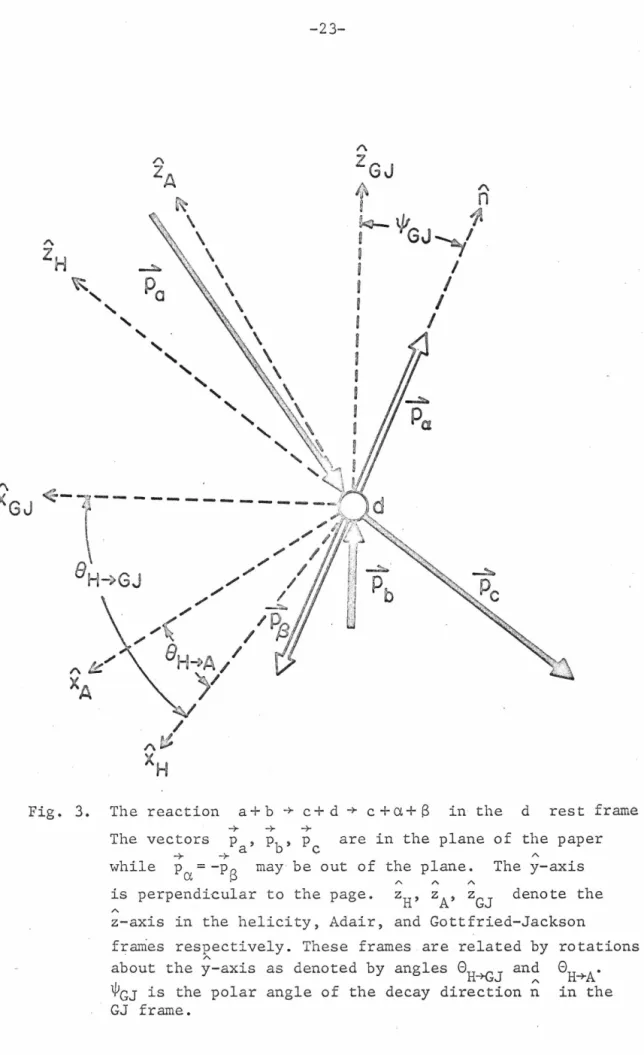
8 may be off the plane. is perpendicular to the page. zH, zA, zGJ indicate. z-axis in helicity, Adair and Gottfried-Jackson. We will show that the tests in the previous section will continue to be applicable. We unfortunately see that for the angular distribution of the nonnal to three-particle decay plane, helicity conservation predicts A~m=~O~_f_o_r~m~>_O_,.
We will show that this model can explain most of the properties of the broad low-mass enhancements observed in diffraction dissociation.

2.0 GeV
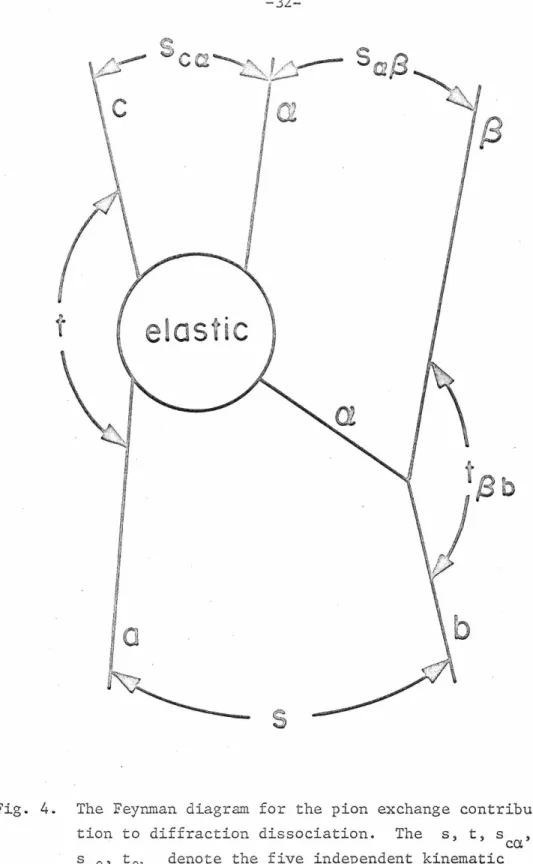
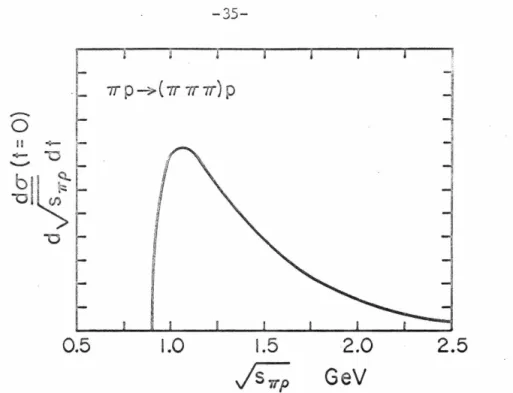
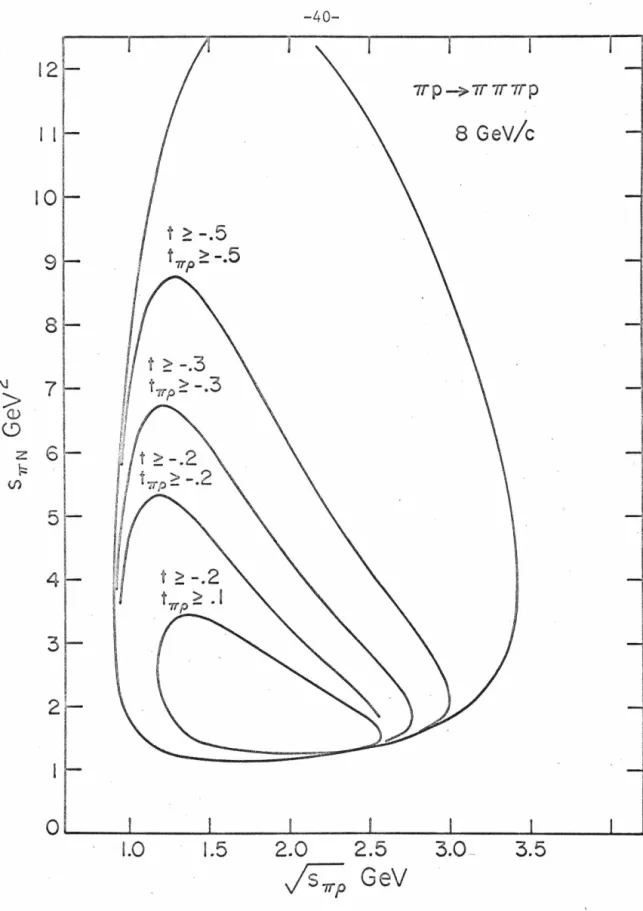
Variation of momentum transfer dependence with mass invariant Empirically it has been found that as a function of t[lS], the differential cross section for producing the above enhancements can be approximated by. To give a simple argument why the OPE model reproduces this behavior, we will consider two limits of saf3 • First, in the small-threshold limit near. However, an equally important contribution comes from elastic aa scattering so that in the extremely high limit of s.
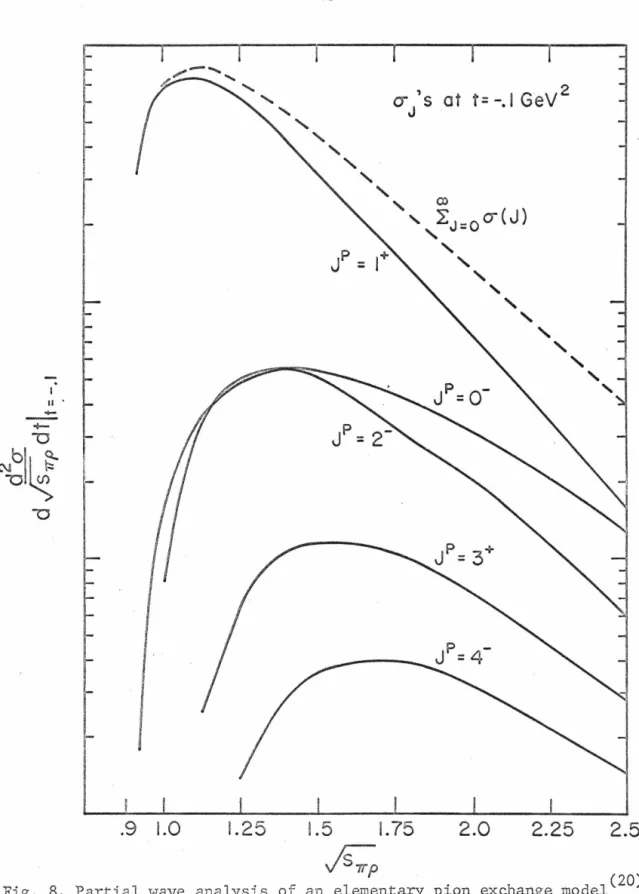
Therefore, in addition to the coupling factors of the spiral, the Deck effect is the most important in the lowest partial wave, i.e. A. We are left with the question of the role of one-pion exchange in diffraction dissociation and its connection with production resonance. The problem is therefore to determine whether the accepted resonances obey the selection rules in the presence of a background that may not.
In the case of resonance dominance, we had a series of "null tests" for helicity conservation and spin-parity selection rules because many of the A£m. The A£ms that were not predicted to be zero in the null tests would also have resonance-resonance terms. This means that, although the null tests are invalid in the presence of an OPE background, there remains a qualitative test for helicity conservation and spin-parity selection rules in resonance production.
Thus, if resonance production obeys selection r~les, the A should be predicted zero in the null tests. A simple pion exchange model appears to account for the properties of the 1 ow mass enhancements that serve in h b d. 1) the shape and position of the improvements (the Deck effect);. If resonance production continues to obey selection rules, the target predicted null in the null tests will now consist of OPE resonance interference terms as well as OPE-OPE terms.
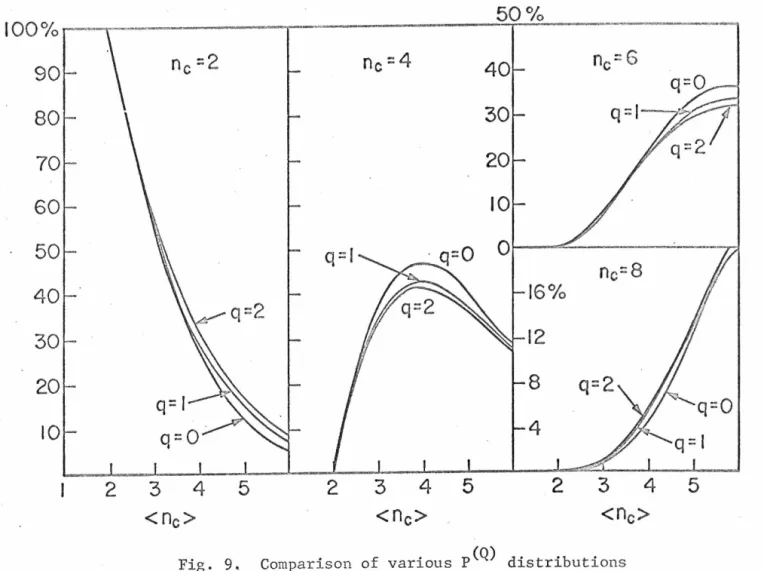
In the case of experiments with unpolarized targets where the final helicities are not measured, the overall angular distribution for two-particle decays is given by. As an example of the type of expressions that result, we give the angular distributions for TIN -r TI(TIN) in the case of helicity conservation. The general considerations we present in this paper are, we believe, independent of the controversial details of these models.
PART II
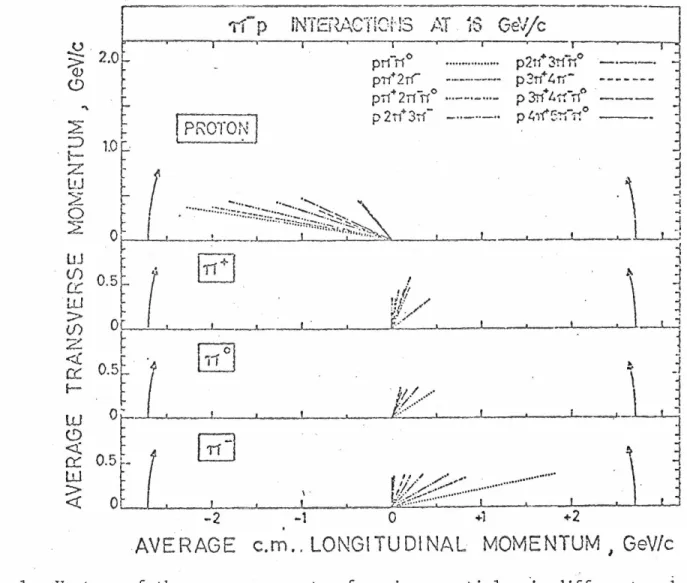
These pawns should be on. to the average, they naturally move in the direction of the N incursion. The pion from the leading p should have. L 7T and should move on average in the direction of incident 7T • Larger mass resonances would result in even smaller average longitudinal moments for their. A model in which the nonconducting pions are considered to be the debris left after the collision of two incident hadrons is called.
Inclusive reactions are reactions in which a few of the final particles are measured and the rest are ignored. reactions in which all final particles are measured. l ' ' n particle distribution, the quantity is important. which in the quantum theory of optics is called the nth order correlation function. TI p -+ TI pTI TI TI TI for different choices of the other's longitudinal impulse. Nevertheless, it is still true that the majority of events are concentrated around low longitudinal impulses at the center of mass.
It was also possible to relate the constancy of the average transverse moments to the asymptotic constancy of the total and elastic sections, as we did intuitively. A state of pions uncorrelated with all species emitting independently and in which the phase of the pion wave function (whose norm is fP(k)) is also fixed as a "coherent state". Since the method is used to describe pions emitted at low energy at the center of mass of the collision, it can be called "coherent pionization".
In the following sections, we will systematically discuss the effects of strong interaction symmetries on the independent emission and briefly examine the independent emission of two-pion resonances. Thus, the coherent state of the particles is a quantized description of the classical radiation of the corresponding field. Let us briefly discuss here the expected form for the i f f (k) characteristics of the distribution functions described in the introduction.
To the extent that the incoming particles are not mesons of the type appearing in the coherent cloud (or, if they are such mesons, have momenta outside the f (k) range), they are independent emission agents. Note that f (k) is an invariant function of k and thus depends on the four moments of the skeleton. Thus again we see that pn describes the distribution of the four momenta absorbed in the meson cloud.
NUMBER OF CHARGED TRACKS
Their distributions, suggested by equation (28), will be modified by taking into account the pion quantum numbers, which we will address in the following sections. In the model discussed in the previous sections, the coherent state must have a fixed electric charge that matches the charge of the skeleton. Since experimentally the emitted pions occupy a small fraction of the available phase space, we expect momentum conservation to be a weak constraint.
Because of the charge constraint, we ask for the conditional probability of emitting n positive and n negative pions simultaneously. In view of the success of the distribution (47), we mention at this point that when we plot all the experiments together, we are closer to the case of a statistical ensemble. It is interesting to note in this connection that the direction of the inequalities in cr.
As a necessary preparation for our discussion in the next section on the implications of isospin conservation, we develop here a formalism for the isospin analysis of pions with identical momentum distributions. The fact that the momentum distributions of the pions are identical is summarized in the assumption. B is a normalization constant equal to. these form 2Cn+l)(n+2) states, characteristic of the fully symmetric combination.
Simple calculation of the number of states shows that in this way we have constructed all possible isospin states of identical pions. The question of the severity of the isospin constraint concerns the extent to which a coherent state can approximately match the isospins of the skeleton. Again, we have limited ourselves to identical pawns and retain the freedom to play with the phases and sizes of the.
The absolute value of s is the asymptotic (i.e. too large ratio of the number of 1i 0 to the number of 'IT • + Therefore we do not consider values too far from unity. The percentages of the content of different isospins in the coherent state If ,Q = 0 > plotted vs. The percentages of the different isospins in the different n particle states included· in If ,Q = 0 > plotted vs.
Charge conservation as the most obvious quantum number constraint leads to changes in the distribution of charged pions that agree well with experiment. The fixed phase of the pion wavefunction is important to minimize the increase of