Introduction
Electronic structure methods and equivariant neural networks
An essential task in molecular simulation is the determination of the potential energy surface based on the laws of quantum mechanics. A host of methods such as Hartree-Fock (HF) and standard Kohn-Sham Density Functional Theory (KS-DFT) then adopt a mean-field variational approach in which the electronic wave function is approximated as a single Slater determinant: where each single-electron orbital𝑖excited by the fermionic creation operator ˆ𝑎†. 𝑖 is represented as the linear combination of an atomic orbital basis|Φ𝜇⟩ =𝑏ˆ†.
Stochastic thermodynamics and score-based generative modeling
In Chapter 4, we discuss that such score-based generative modeling techniques can enable the prediction of complex molecular structures important for both molecular biology research and drug discovery applications.
Structure of the thesis
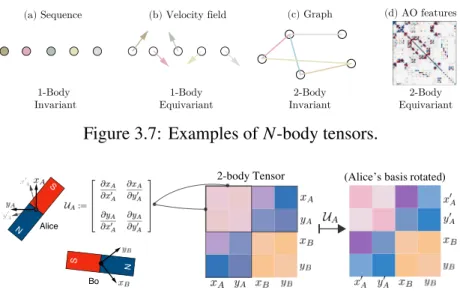
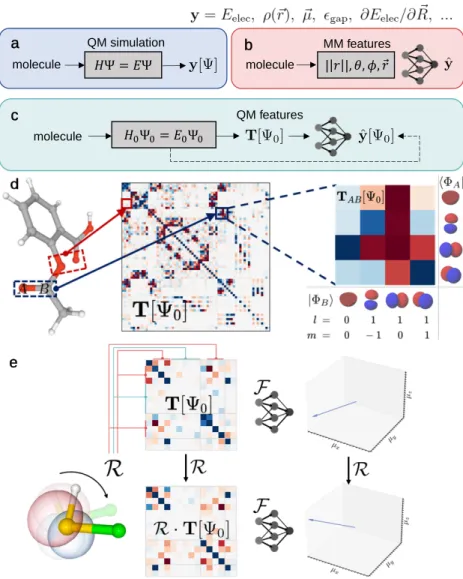
Although independent of the choice of local reference frame e𝑢, its coefficients T (i.e. the 𝑁-body tensor) vary when rotating or reflecting the basis𝑢 :={e𝑢;𝑣𝑢;𝑣𝑢}, i.e. the number of vectors of the order 𝐿 -1 tensor h𝑡𝑢 that transform under the 𝐿-th irreducible representation 𝐺𝑢 (i.e. the multiplicity of 𝐿 in h𝑡𝑢).
Orbital-Based Deep Learning for Molecular Electronic Structure . 6
Method
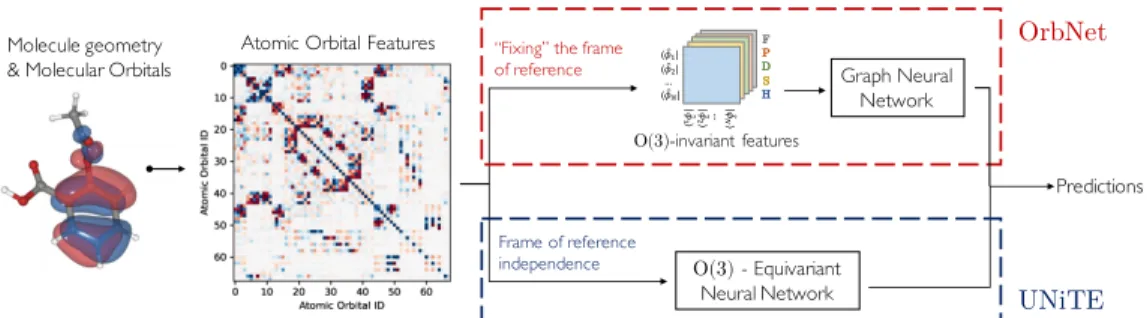
The one-electron density matrix of the molecular system in the AO basis is then 𝑃𝜇 𝜈 =2. Features include expectation values of Fock operators (F), density (P), basis Hamiltonian (H) and overlap (S) in the SAAO basis.
Numerical results
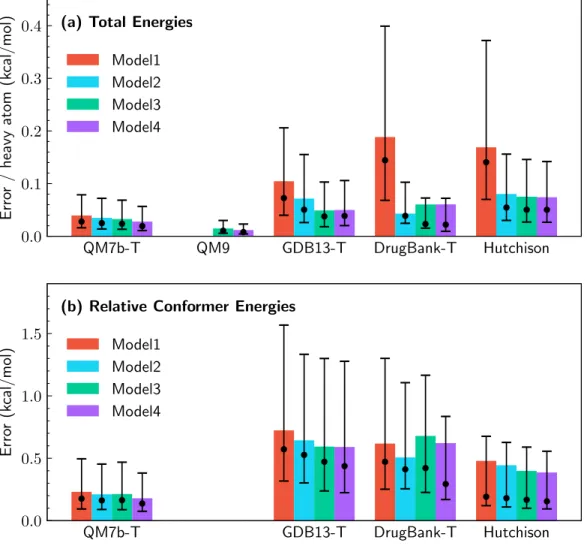
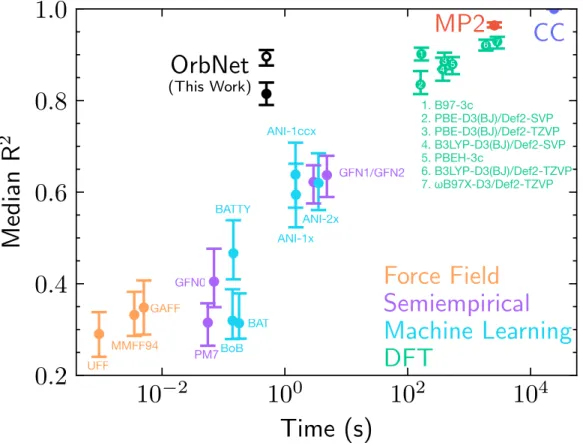
For the Hutchison conformer data set of drug-like molecules ranging from nine to 50 heavy atoms, the accuracy of the various methods was evaluated using the median R2 of the predicted conformer energies against the DLPNO-CCSD(T) reference data and the computational time evaluated at to a single CPU core.[64] The solid black circle indicates the median R2 value (0.81) of the OrbNet prediction against the DLPNO-CCSD(T) reference data, as with the other methods; this point provides the most direct comparison with the accuracy of other methods.
Analytical nuclear gradient theory
The solid black circle represents the average R2 value from the OrbNet predictions relative to the DLPNO-CCSD(T) reference data, as for the other methods. The gradient for the GFN-xTB model 𝐸𝑥TB has been previously reported [60], and the gradients of the neural network with respect to the input features 𝜕 𝐸𝜕NNf are obtained using automatic inverse mode differentiation [69].
Improved data efficiency via multi-task learning
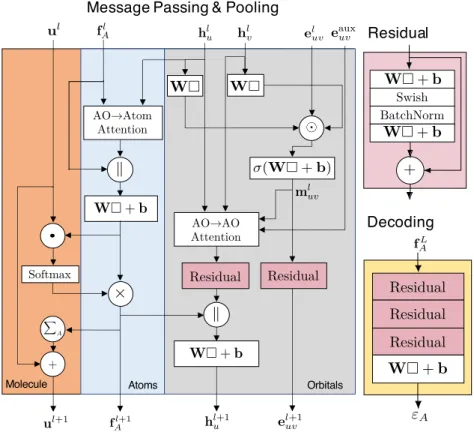
For the prediction of both the electronic energies and the auxiliary targets, only the last atom-specific attributes, f𝐿𝐴, are used, because they themselves consistently incorporate the effect of the whole molecule and node- and edge-specific attributes. The atom-specific targets we use are similar to those introduced in the DeePHF model [47], obtained by projecting the density matrix into a basis set that does not depend on the identity of the atomic element.
Conclusions
W
Appendix
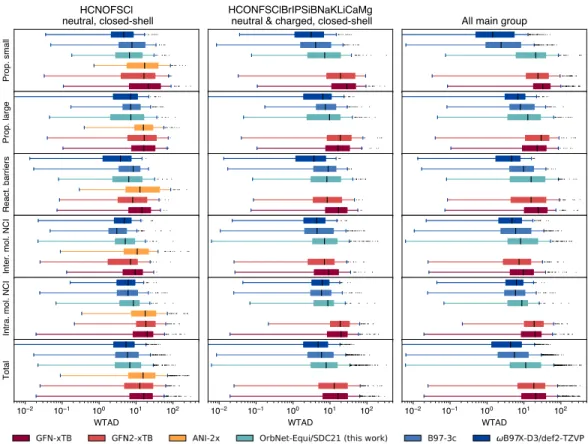
UNITE is trained to predict the quantum chemistry properties of interest based on the input T = (F, P, S, H) with possible extensions (e.g. the energy-weighted density matrices). Table 3.7: Subset averageWTMAD-2(WTMAD-2𝑖=1 𝑁𝑖 . Í 𝑗WTAD𝑖,𝑗,see methods3.8)on theGMTKN55 set of benchmarks, reported for all possible methods considered against the CSD, is against the CCSD Considered-in-Value. es. Standard error of the mean is reported in parentheses. For cases in which no response with a subset is supported by a method, the results are marked as "-". The OrbNet-Equi/SDC21(filtered) column corresponds to OrbNet-Equi/SDC21 evaluated on reactions consisting of chemical elements and electronic states appearing in the SDC21 training dataset, as shown in Figure 3.6b. LDSM site is defined analogously, but averaged for residues that are within 6.0 Å of. the ligand in the ground truth structure. 4.34).
Equivariant Neural Networks for Orbital-Based Deep Learning . 39
Method
The inputs to the neural network built on Ψ0 comprise a set of matrices T[Ψ0] defined as one-electron operators ˆO [Ψ0], which are represented in atomic orbitals (Figure 3.1d). Motivated by mean-field electronic energy expressions, the input atomic orbital features are chosen as T= (F,P,H,S) using the FockF, densityP, core HamiltonianH and overlapping S matrices of tight-binding QM models (see Methods 3.7), except unless otherwise specified. 3.4), which is fulfilled by our sensitive neural network design in OrbNet-Equi (Figure 3.2).
Performance on benchmark datasets
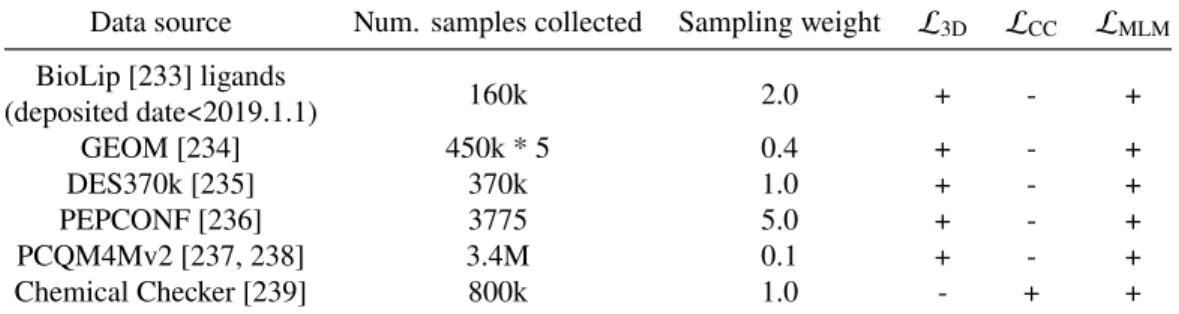
For𝑈0(Figure 3.3a), the direct-learning results of OrbNet-Equi match the state-of-the-art kernel-based ML method FCHL18/GPR [125]. Additionally, for dipole moments 𝜇® (Figure 3.3b), OrbNet-Equi exhibits steep learning curve slopes regardless of the training strategy, highlighting its ability to learn rotation-covariant quantities without sacrificing data efficiency. Results (Appendix Table 3.2-3.3) showed that OrbNet-Equi obtained energy and force prediction errors consistent with state-of-the-art machine learning potential methods on the MD17 dataset suggesting that our method also generalizes effectively over the conformational degrees of freedom apart from being transferable over the chemical space.
Accurate modeling for electron charge densities
Transferability on downstream tasks
Notably, on the G21IP dataset [148] of adiabatic ionization potentials, we find that the OrbNet-Equi/SDC21 model achieves significantly lower prediction errors than semi-empirical QM methods (Figure 3.5e, Table 3.7), although samples of open-shell There signatures are expected to be rare from the training set (Methods 3.8). OrbNet-Equi/SDC21 predictions are found to be highly accurate on this subset, as seen from the WTMAD with respect to CCSD(T) being on par with the DFT methods on all five reaction classes and significantly outperforming ANI -2x and the GFN family of semi-empirical QM methods [60, 62]. When evaluated on the collection of all GMTKN55 tasks (Figure 3.6, 'Total' . Panel), OrbNet-Equi/SDC21 maintains the lowest median WTMAD among methods considered here that can be performed at the computational cost of semi-empirical QM calculations .
Discussion
Furthermore, we note that failure modes can be identified on some highly extrapolative subsets to diagnose cases that are challenging for the QM model used for characterization (Table 3.7). At the population level, the distribution of predictive WTMADs by GMTKN55 tasks also differs from that of GFN2-xTB, which means that the further inclusion of physics-based approximations in the QM featurizer can complement the ML model and thus the accuracy limit of semi-empirical methods can be pushed into a regime where no known physical approximation is feasible. Since the framework presented here can be easily extended to alternative quantum chemistry models for molecular or material systems, we expect OrbNet-Equi to be of general benefit to studies in chemistry, materials science, and biotechnology.
The UNiTE neural network architecture
Within those modules, the matching layer assigns the channel indices of 𝑡 to the indices of the atomic orbital basis. Note that the auxiliary basis ˜Φ𝐴 is independent of the atomic numbers, and thus of the resulting h𝐴. C is the molecular orbital coefficient defining Ψ0, and𝝐 is a diagonal eigenvalue matrix of molecular orbital energies.
Dataset and computational details
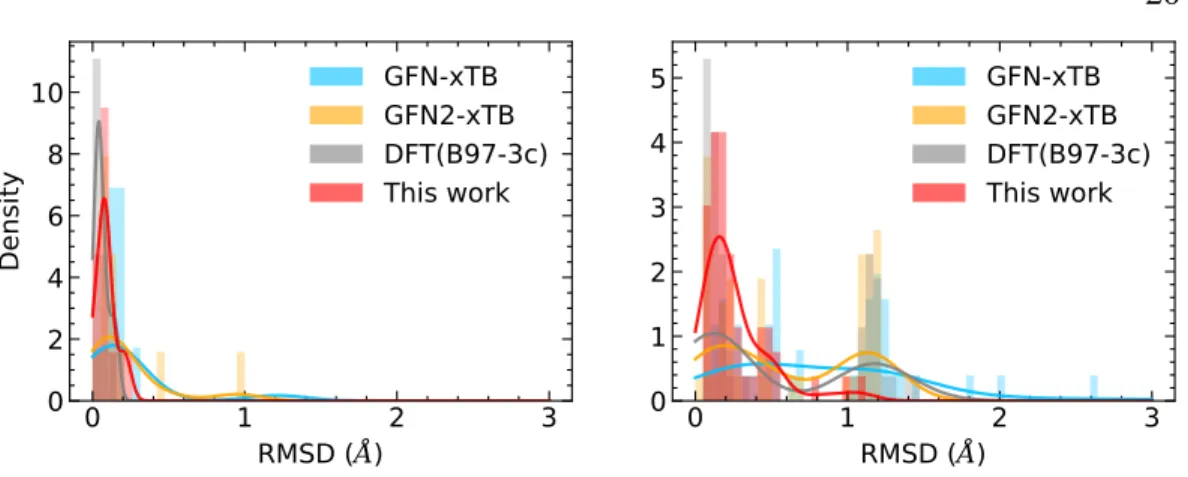
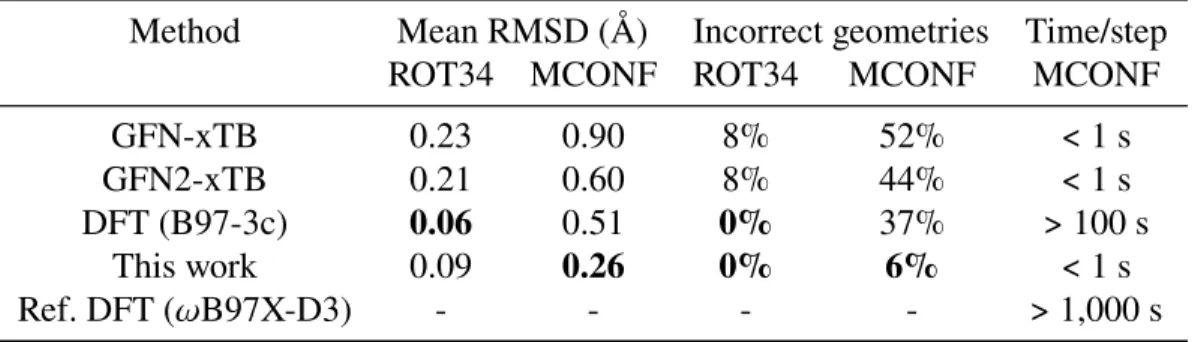
We note that two basic methods used slightly different normalization conventions when computing the errors of the mean density of the data set𝜀𝜌, (a) computing𝜀 on the test set [131]. We follow their individual definitions for the mean𝜀𝜌 for the quantitative comparisons described in the main text, namely. The geometry optimization accuracy in Figure 3.5d and Table 3.5 is reported as the symmetry-corrected root mean square deviation (RMSD) of the minimized geometry versus the reference level of theory (𝜔B97X-D3/def2-TZVP) calculated over molecules of placed. .
Additional theoretical results
The atomic orbital features discussed in the main text fall into this class, since the angular parts of atomic orbitals (i.e. spherical harmonics𝑌𝑙 𝑚) form the basis of the irreducible representations of group SO(3). For a tensorTˆ ∈ V⊗𝑁 we call the coefficientsTofTˆ in the 𝑁-th direct products of basis{𝝅𝐿 , 𝑀 ,𝑢;𝐿 , 𝑀 , 𝑢} an 𝑁-body tensor, ifTˆ =𝜎(T)ˆ for any permutation𝜎 ∈ Sym(𝑁) (i.e. permutation invariant). Note that the vector spaces 𝑉𝑢 do not have to be embedded in the same space R𝑛 as in the special case from Definition S1, but can come from general ones.
Appendix
UNITE is naturally extended to inputs that possess extra feature dimensions, as in the case of AO features described in Section 3.7, the extra dimension is equal to the cardinality of selected QM operators. To sample from the reverse-time SDE, we use the contact predictor to generate derivative contact maps ˆLand parameterizes the geometry for 𝑞𝑇∗(·|x˜,Lˆ) — the initial state of reverse-time SDE — by x (0) to replace. in 𝑞𝑇∗ with the backbone template ˜x and the ligand-C𝛼 relative drift coefficient c with the prediction dec(L). The input to the protein encoder is (i) the one-hot amino acid type (20 standard residues + 1 "unknown" character) encoding of the 1D sequence𝑠, (ii) the backbone (N,C𝛼,C) coordinates of a disordered protein structurex (𝑡) sampled from the forward SDEs described in Table 4.1, and (iii) a random Fourier encoding of the diffusion time step𝑡.
Multiscale Equivariant Score-based Generative Modeling for
Introduction
However, computational prediction of protein–ligand structures coupled to receptor conformational responses is still hampered by the prohibitive cost of physically simulating slow protein state transitions, as well as the static nature of existing protein fold prediction algorithms [5, 189]. A computational method that rapidly generates protein-ligand complex structures can therefore greatly aid the process of unconventional target identification and rational allosteric modulator design. NeuralPLexer can generalize to ligand-unbound or predicted protein structure inputs once trained only on experimental protein-ligand complex structures that are not coupled to alternative protein conformations.
Method
The architecture of ESDM (Figure 4.1e) is inspired by previous works on 3D graph and attentional neural networks for point clouds rigid-body simulations [218]. Explicit nonlinear transformation on vector features performed only on rigid-body nodes by a coordinate-frame inversion mechanism, such that the node update blocks are sufficiently expressive without sacrificing equivariance or computational efficiency. The non-trivial actions of a parity-inversion operation on rigid-body nodes ensure that ESDM can capture the correct chiral-symmetry-breaking behavior that satisfies the molecular stereochemistry constraints.
Results
On the contrary, 3D coordinates are updated only for atomic nodes, while the rigid body frames (t,R) are passively reconstructed according to the updated atomic coordinates, eliminating numerical problems related to adjusting quaterion or axis angle variables when manipulating objects can be circumvented with a rigid body. . The accuracy of the protein binding sites is measured by the lDDT-BS metric [226] with cutoff parameters consistent with CAMEO [227]. Input backbones are obtained using template-free AlphaFold2 (AF2) predictions of 154 selected chains whose TM score [228]>0.8 and lDDT-BS<0.9 from the aforementioned PDBBind test set, a subset representing cases where AF2 the global protein folding but unable to reproduce the exact binding site structure of the bound state.
Discussion and outlooks
Here we apply a diffusion-based inpainting strategy to jointly sample the ligand and protein structure for a cropped region within 6.0 Å of the ligand conditioning on the uncropped parts of the protein. As a preliminary investigation, we use the ligand-unbound (apo) crystal structure of PDB as the input backbone template and fix the ligand conformation to ground-truth coordinates during sampling. We anticipate integrating state-of-the-art techniques for learning protein representations, such as the use of evolutionary sequence signals, pre-trained language models or higher-level attention mechanisms, and training on large-scale structure datasets to further improve the methodology and facilitate applications in various downstream molecular design problems .
Appendix
The random Fourier encoding of the diffusion time step𝑡 is also coupled to the representations of the ligand atoms from the ligand graph encoder and transformed by a two-layer MLP. The neural network architecture of the proposed Equivariant Structure Diffusion Module (ESDM) is summarized in Figure 4.5. All receptor residues not within 6.0 Å of the ligand are set to ground-truth coordinates, with residue- and atom-wise time coding set to zeros.
TorchANI: A Free and Open Source PyTorch-Based Deep Learning Implementation of ANI's Neural Network Potentials”. In: Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining.
![Figure 3.3: Model performance on the QM9 dataset. (a-b) Test mean absolute error (MAE) of OrbNet-Equi is shown as functions of the number of training samples, along with previously reported results from task-specific ML methods (FCHL18[125], FCHL19[126], S](https://thumb-ap.123doks.com/thumbv2/123dok/10408482.0/63.918.222.700.122.642/figure-performance-absolute-functions-training-previously-reported-specific.webp)