Because cbits can be encoded into qubits and ebits can be fixed by sending qubits, the noiseless quantum channel (in this narrow sense) is the strongest of the three. If she gets only a copy of the quantum state and not a description, we describe the source as hidden and the encoding as unaware (or blind).
Introduction
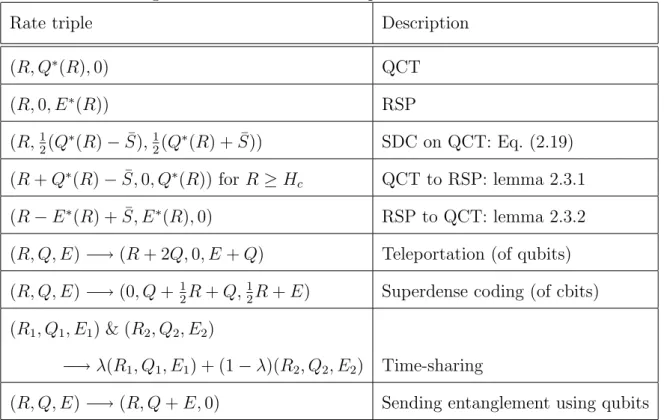
In the spirit of [11], this new protocol can be seen as the "father" of the noiseless visible mode communication protocols. The remainder of this chapter is structured as follows: We begin in Section 3.2 by presenting the universal protocol for super-dense coding of entangled states and then prove its optimality together with that for the associated remote state preparation protocol in Section 1.3.
The universal protocol
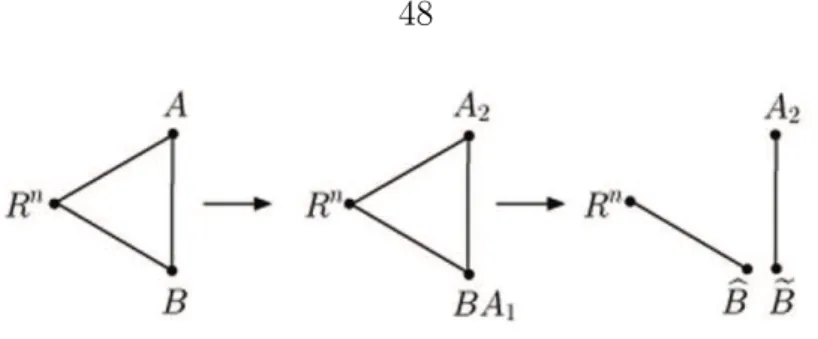
Alice and Bob share a maximum entangled state of logdB = 12(logdS−logλmax) + o(logdS) ebits on their joint system AB. By standard arguments, this will ensure that there exists a unitary UA2B such that S(TrA2UA2BϕSUA†2B) is close to logdB for all states on S that are maximally entangled with A01.
Optimality of the protocol
Since EF cannot increase below LOCC, the right-hand side is also a lower bound on the . The protocol including teleportation requires Q+E ebits, so the lower bound on Q+E also follows from Proposition 1.3.1.
Protocol for a memoryless source
The Gentle Measurement Lemma, called the tender operator inequality in [35], implies, together with a simple application of the triangle inequality, that kϕAin1S −σAin1Sk1. If in is typical, meaning it is in the set Tp,δn (which occurs with a probability of at least 1−m/δ2), then that is also true. 1.26) gives a bound on the effective dimension of the system S since σiSn ≤Πnρ,δ for all in.
Identification
The negligible communication costs are common in identification theory: the classic identification power of a piece of shared randomness supplemented with negligible communication is a bit. Nevertheless, by appealing to Theorem 1.2.3, we see that the asymmetry in the asymptotic limit disappears if negligible communication is allowed.
Discussion
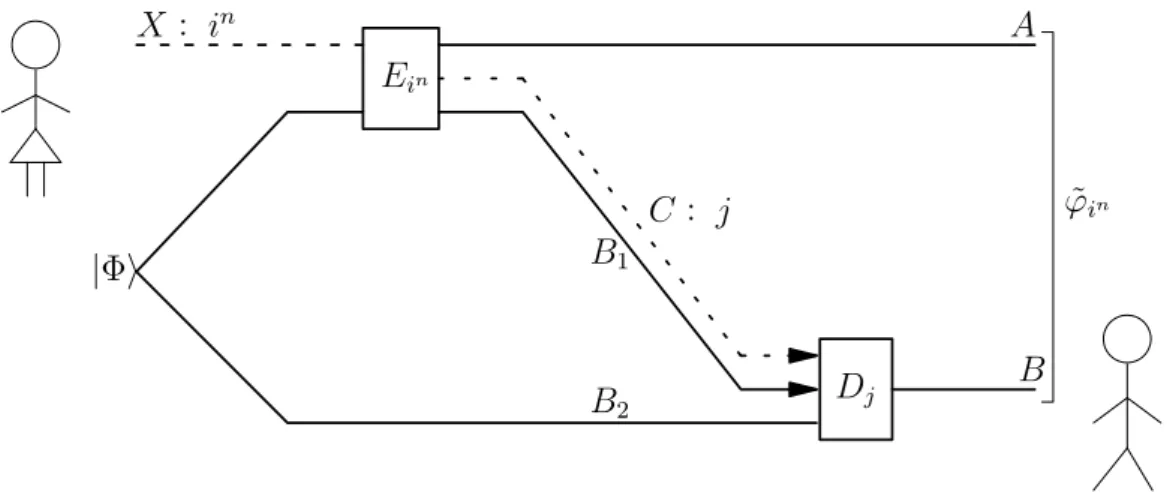
We specifically study the version of the problem in which the sender is given notice of the state to be communicated. In this environment, a trade-off arises between the three resources, some parts of which have been previously explored in the contexts of the quantum-classical trade-off in data compression, remote state preparation and superdense coding of quantum states, each of which amounts to only two of these three resources are allowed. This appears to be feasible through trade-off coding and suitable time sharing between optimal protocols for cases involving two resources out of the three mentioned above.
The functionS(ρ) is the von Neumann entropyS(ρ) = −TrρlogρandS(E) the von Neumann entropy of the average state of the ensemble E.
Definition of the problem and previous results
At the other extreme, the cbit rate is minimized (at least for irreducible resources) by a protocol that achieves rate (χ(EB),0, S(EB)). We have the following theorem from Ref. 2.6) with the classical channel sp(j|i) and the number of states in E.
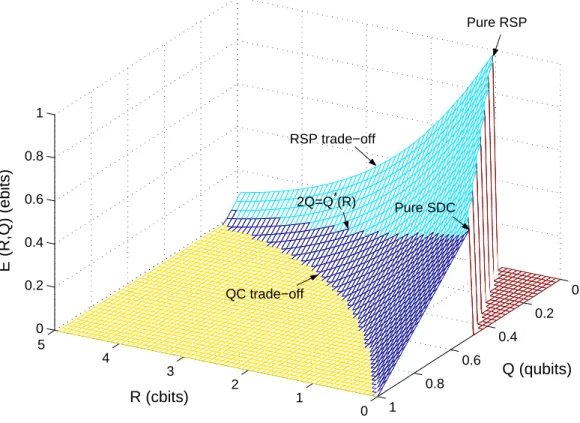
E = 0: Quantum-classical trade-off (QCT)
E∗ is convex, continuous and strictly decreasing in the interval in which it takes positive values. Likewise, the optimal point when Q= 0 is given by (H(pi),0,0), which means that Alice has no better strategy than to communicate the label to Bob. More generally, when the ensemble is allowed to contain entangled modes, the techniques of Refs. is easily adapted to give a formula for .
Q∗ is convex, continuous, and strictly decreasing in the interval in which it takes positive values.
Proof Since (0, S,0) and (0, χ/2, S −χ/2) (S and χ are defined in the introduction) are both feasible rate triples, any convex combination of both is a feasible rate triple corresponding to a time shared protocol. However, by using quantum communications to achieve entanglement, protocols that achieve this speed can be turned into protocols with triple the speed. Our evaluation of E∗(R, Q) will be achieved via operational reductions of the three extreme cases we have now completed, just like Theorem.
Later we will also have occasion to use the following analogue of the QCT and RSP constructions.
Relating optimal QCT and optimal RSP
50], however, shows the existence of just such an operational reduction, but only under the assumption that the mixed-state compression conjecture is true. Note that this inequality is true whether R is greater or less than Hc. Prove LetHc≤R1 and consider R=R1+Q∗(R1)−S.¯ Rise a strictly increasing function of R1 by the definition of Hc, taking all values χ ≤ R.
The triple trade-off
Armed with these observations, we can now proceed with the proof of Theorem 2.4.1 in the high-entanglement region. R1+Q∗(R1)−S,¯ 0, Q∗(R Note that teleportation is appropriate here instead of RSP because the encoding map corresponding to the first triple will generally produce complicated entangled states between Alice and Bob, conditioned on the classical bits being communicated.Teleportation will preserve this entanglement.).
In case of subadditivity of the von Neumann entropy, the first term is less than or equal to S(X), which again is not more than log dimX. Moreover, because ρ is separable across the X/AB cut, S(X|AB) ≥0. This follows immediately from the concavity of the entropy [60, 61].). The last ten years have seen great progress in the field, including, among many other discoveries, the determination of the classical capacity of a quantum channel [62, 63], the capacity of entanglement-assisted channels [64, 65], the quantum channel capacity of a quantum channel and the best ways to use noisy entanglement to extract clean entanglement [69] or send classical information [70].
In this article we provide direct proof of the mother protocol, or more precisely, of the existence of a protocol that performs the same task as the mother.
The family of quantum protocols
A source of the form hN :ρSi is a channel with input system S that is guaranteed to behave as channel N if the reduced input state density operator onS is ρS. Thus, on the left-hand side of the inequality, the state is shared between Alice and Bob, while on the right-hand side, this same state is allocated only to Bob. Transforming the first situation into the second means that Alice transfers her part of the state to Bob.
Since the mother's relationship to entanglement distillation and communication supplemented by noisy entanglement is explained in detail in the original family paper, we will not describe the connections here.
The fully quantum Slepian-Wolf protocol
Unlike the mother, where Alice and Bob share a mixed state (ϕAB)⊗n, for the father protocol they share a noisy channel NA0→B. 3.1), reveals the two to be strikingly similar: to go from one to the other, it suffices to replace channels with states and vice versa, as well as to replace the reference R with the environment E. Since no information leaks to the environment at any stage will Bob hold a cleanup of the A2Rn system after step 2, regardless of the choice of UA.
Bob's UB isometry will be the one that takes the clearance he holds by taking A2 to the one approximating |ΦiA2B˜(|ϕiRBˆ)⊗n.
Fully quantum Slepian-Wolf: one-shot version
Also, the upper bound on the right is expressed entirely in terms of the dimensions of the spaces involved and the purities Tr[(ψAR)2], Tr[(ψA)2] and Tr[(ψR)2]. In the tensor power source setting, both dimensions and purities can be replaced by functions of the corresponding entropies, but in the one-shot setting they must be distinguished. The third follows from F2 = I and the explicit inclusion of previously implicit identity operators to aid in the evaluation of the trace in line four.
The formula then follows after a bit of algebra, using FA2R=FA2 ⊗FR and Rank(Π±A) =dA(dA±1)/2. ut The next step is an exact evaluation of the Hilbert-Schmidt analogue of the one-time, fully quantum Slepian-Wolf inequality. where p and q are defined as in Eq.
Fully quantum Slepian-Wolf: i.i.d. version
The first line is Cauchy-Schwarz, the second is an integral that we have already performed in the proof of Lemma 3.3.3, and the last is an application of Eq. because R is the reference system and is therefore not allowed to take an active part in the protocol. From Theorem 3.3.1, we find that. 3.31) Therefore, if logdA1 ≥n[I(A;R)/2 +δ] for every δ >0,σA2Rtyp and Alice sends A1 to Bob, he will end up holding a close approximation to a clearing of ϕR⊗ n for enough n. In a good approximation, it will also do a cleanup of the residual state on Alice's system. 3.29) to prove how entangled we expect from the state. 3.32) Hence, Alice and Bob will share the maximum entanglement provided that Alice sends the cube to Bob at a positive rate.
As discussed after Theorem 3.3.1, Bob can apply a transformation, taking A1B to ˜BBˆ with the final condition|ξiA2B˜BRˆ satisfying°.
Father from FQSW
We will now call the type class variant FQSW result but now with the subsystems playing different roles: If the FQSW unitary U is applied to B3R, we see that the effect would be to disconnect the registers corresponding to the FQSW picture to A2 andR, meaningRandE, respectively. This is exactly what is desired, because there will exist a decoding protocol for Bob to complete the father, provided that, after applying the channel N, he keeps the entire purification of R. Of course, the application of U to B3R is not possible, because as always, the reference system cannot participate in the protocol.
Bob performs VB3B→B˜Bˆ and obtains a state where the ˜B system approximately clears the reference system, which plays the role of A2 in the FQSW image.
Correlated source coding: distributed compression
To begin, fix n > N(²) and let WA and WB be the environments for the Stinespring dilations of the encoding operations EA and EB. The first inequality is an application of the triangle inequality, while the first equality is because AnBnRn is a pure condition. Combining and using the subadditivity of the Von Neumann entropy (3.54) and the fact that the overall state is pure, we have.
The first similarity follows from the fact that the initial environment is a pure unentangled state and from the unitary invariance of the Von Neumann entropy.
On efficiency
The corresponding inner boundary of the achievable speed range SW(ϕ) would therefore be determined by the inequalities. Since the Schumacher compression part of the fully quantum Slepian-Wolf protocol can also be implemented in polynomial time [84], we conclude that the coding part of the mother can be implemented efficiently. Thus, the coding for the father can be found and implemented in polynomial time, as well as for its children, classical communication via entanglement and quantum communication via a noisy channel.
Cost of classical communication in distributed quantum information processing - a generalization of quantum communication complexity. Phys.