It was a pleasure to share this adventure with the people in the Department of Applied Mathematics. The operator that maps the velocity vector to vorticity, (−∂y, ∂x) ξ: The velocity spatial variable in the pressure direction, defined as ξ= p.
Introduction
In the fourth chapter we improve the hyperbolic equation of the two-phase flow equations. With this expression for the rate, the equation for the saturation of the wetting phase can be written as So the two solutions coincide and the uniqueness of the solution in the pressure line frame follows from.
In the next step of the method we will impose that the minimum distance is hmin. The resulting O(−1) equation implies that the two-scale limit of saturation does not depend on the fast variable ξ along the streamlines. This is another indication that the pressure streamline frame correctly represents the structure of the flow.
We will use the higher saturation and velocity moments to model macrodispersion. The basis functions satisfy the same equation as the pressure in the coarse blocks of the domain.

Resolved Scheme
The Porous Media Equations in the Cartesian Frame
Derivation of the Physical Model
- Pressure Equation
- Saturation Equation
- Model Problem
We included the effects of the compressibility of the phases and the porous medium and of the capillary pressure. We can solve for the velocities of each phase in terms of the average velocity and the capillary pressure.
Resolved Scheme
- Finite Volume Method for the Pressure equation
- Finite Volume Method for the Saturation Equation
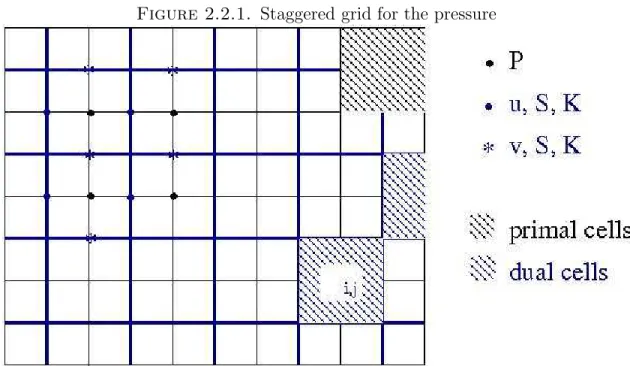
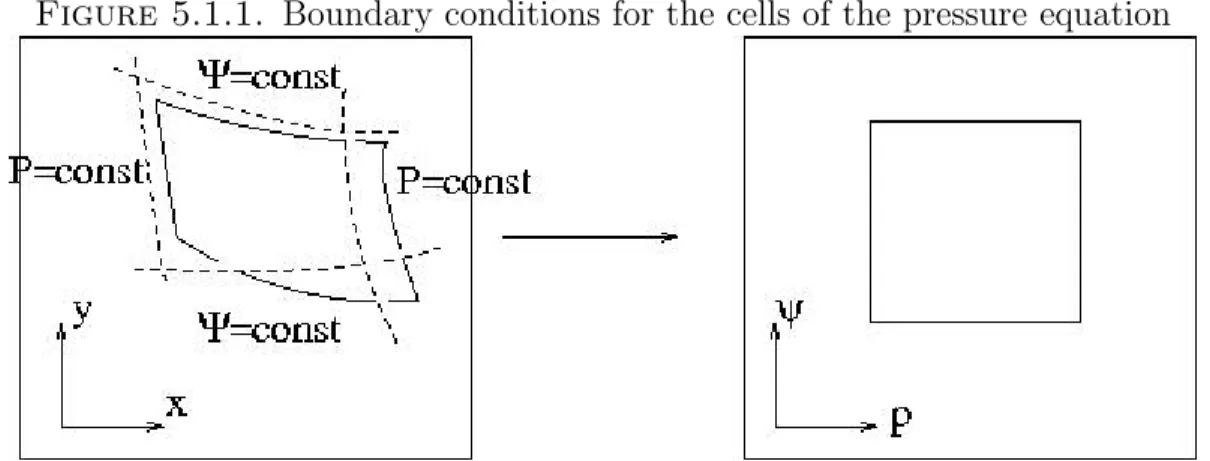
In a finite volume scheme for the pressure equation, the permeability and velocity are defined at the ends of the double cells and the pressure is defined at. For the spatial discretization of (2.2.2), the cells of the finite volume scheme are the dual grid cells.
Some Numerical Results
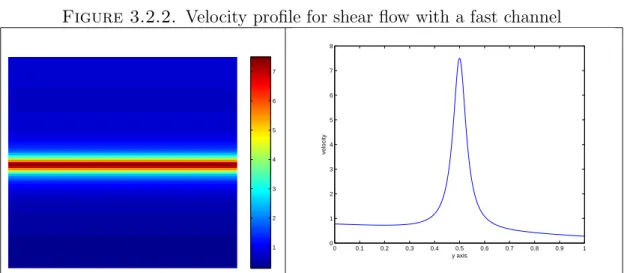
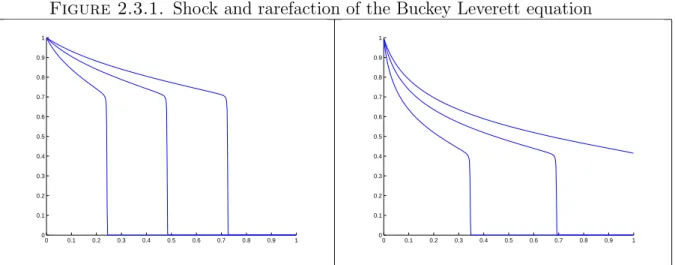
For a general nonconvex scalar conservation law, Osher [42] discovered a functional relation for its saturation and flux in terms of the similarity variable xt. In flows in two and three dimensions when the velocity changes rapidly across the streamlines, the saturation profile develops fingers along the fast flow channels.
An Adaptive Framework for Solving the Porous Media Equation 24
The Pressure-Streamline Frame
- Coordinate Transformation
- Entropy Solutions
- Invertibility
- Adaptivity
- Extension to Three Dimensions
In this section, we demonstrate that the entropy solutions of the two-phase flow equations coincide. To determine the correct entropy equation for our equations, we start from the weak form of the entropy equation in the Cartesian frame. Then that solution coincides with the solution of the two-phase flow equations in the pressure streamline framework (3.2.2) together with the entropy condition (3.2.7).
The first two terms are the Lagrangian time derivative, which is the time derivative of the saturation in the moving frame.
Numerical Implementation
- Computing Ψ,v 0
- Natural Neighbor Coordinates
- Finite Volume Scheme for the Saturation in p, ψ
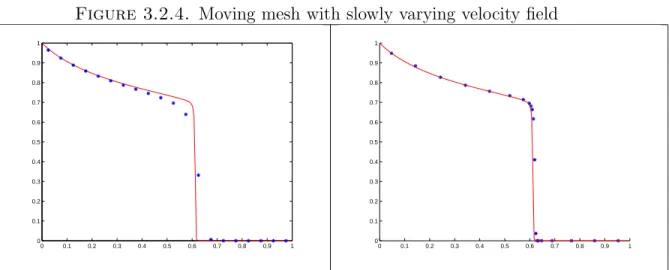
- Moving Mesh
The same conserved quantity can be reached by changing the coordinates in the weak formulation of the conservation law. We will choose the latter based on the fact that the second time derivative of saturation comes from (3.3.1). This is because when calculating the control function at time t+ ∆t we use the saturation at time t and not at time t+ ∆t.
For correct winding of the interpolation equation from (3.3.4), we rewrite the convection term as a conservative convection term and forcing.
Numerical Results
The idea to consider with a strict derivation of the two-scale limit for a linear flux. Average equations (4.1.10) with respect to ψ we find an equation for the average of the saturation. In deriving the equation of the two-scale limit, we homogenized the fine saturation equations.
Looking at the last equation, we can understand the influence of the macrodispersion in the scaled-up equation (4.2.2). Because the order of the highest derivative in the equation has increased, we need additional boundary conditions. A second disadvantage of the conformal MSFEM is the presence of resonance errors in the basis functions near the cell boundary.
Initially, the exact solution of the pressure equation in the pressure line frame is of course the identity P(t = 0, p0, ψ0) = p0. In this work we treated the homogenization of the saturation equation assuming that the velocity does not depend on the saturation.
Upscaled Scheme
Upscaling One-Phase Flow
Two-Scale Limit
- Context of the Present Work
- Derivation of the Two-Scale Limit for Linear Flux
- Derivation of the Two-Scale Limit for Nonlinear Flux
- Convergence Rate to the Two-Scale Limit
The limited sense of convergence has preserved all information about the full two-scale limit. Note 4.1.2. We can give an indication why the two-scale limit of the saturation will not depend on a fast time variable if the initial condition SIC(p, ψ, ζ) does not depend on p. To derive the two-scale limit, we divide both sides of equation (4.1.2) by Jacobian, multiply by a test function φ and integrate.
Since the two-scale limit ˜S exists, S will converge to it, with φp,φt, andv0 playing the role of the test functions of the theorem.
Comparison with the Cell Problem in the Cartesian Frame
Comparison with the cellular problem in the Cartesian framework. Equations (4.1.10) will be rewritten in the form of an equation for the average. We want to compare the homogenized equations derived above with the corresponding equations in Cartesian variables. Homogenized equations in Cartesian variables, as derived by Westhead [53], are defined in terms of saturation averaged over coarse blocks of S and S00 fluctuations.
Note that while the fluctuations S0 in the pressure streamline frame depend only on one fast variable, the fluctuations S00 in the Cartesian frame depend on two fast variables.
Weak Limit and Full Homogenization
In a sense, in the pressure line frame, the projection operation, which was performed by limiting the oscillatory test functions, cleanly removed a fast variable and reduced a fast dimension to arrive at the cell problem of (4.2.3 ). In the Cartesian framework, the projection operation remained in the equations in the form of P and Qand, the rapid change along the flow was not clearly removed. To invert the Laplace and Fourier transforms we use the fact that there is a second Young measure dµψ.
Efendiev and Popov [24] extended this method for the Riemann problem in the case of nonlinear flux.
Designing an Upscaled Model from the Two-Scale limit
- Physical Interpretation of the Subgrid Forcing
- Numerical Averaging across Streamlines for Linear Flux
- Numerical Averaging across Streamlines for Nonlinear Flux
The first term corresponds to diffusion whose magnitude depends on the two-point correlation of the velocity field, and the second corresponds to a convection. We note that also the definitions of the average saturation and its fluctuations (4.2.1) are easier to understand in the context of a numerical scheme. The term within the time integral is the covariance of the velocity field along each streamline.
Due to the dependence of the jump in saturation on the mobility, we expect this approximation to be better for lower mobilities.
Implementation
- Considerations for the Macrodispersion
This expression is very similar to the one obtained in the linear case; however, here the macrodispersion depends on the past saturation via the coarse feature equation. To calculate the macrodispersion term, we do not impose a flux on both domain boundaries.
Numerical Results
- Macrodispersion Modeling
- Saturation Snapshots
- Accuracy and Computational Cost
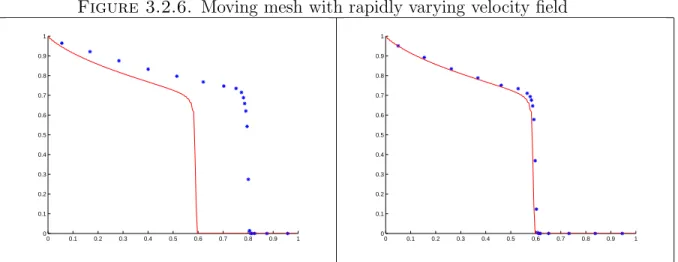
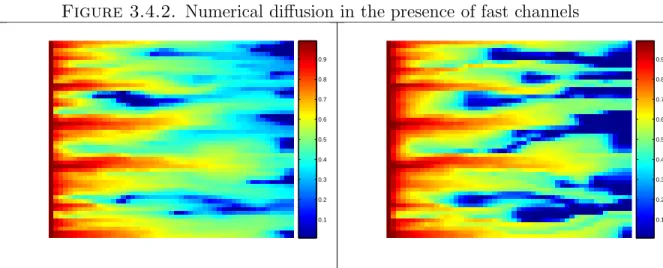
Making sure that the numerical diffusion is smaller than the macrodispersion can generally be achieved by using coarse cells elongated in the ψ direction. In the calculations of the next section, we see that the moving mesh implemented accurately solves the equation for S with macrodispersion even though the macrodispersion is calculated on the adaptive grid, which is fine close to the shock of S and coarse away from it. In the experiments with the fast channel, the SPE10 36 permeability field, we see an artifact along the fast channel in the saturation pictures.
We use the same parameters as in the previous section and report the results for the permeability with a fast channel (SPE10 36) in table 9.
Upscaling Two-Phase Flows
Pressure Equation
- The Multiscale Finite Element Method (MSFEM)
- The Modified MSFEM
- The Modified MSFEM in the Pressure-Streamline Frame
- Derivation of the Equations
This experimental validation shows that the basis functions really capture most of the fine-scale behavior and that the MSFEM method rests on a good idea. The motivation is that the connection of the fast channels will be reflected in the initial pressure and through the cell boundary condition also in the basis functions. For the basis functions in MSFEM, we choose a linear boundary condition on edges with p0 = ihc and no-flux boundary conditions on edges with ψ0 = jhc.
In our method, the long-range correlations of the basis functions are captured by the coordinate frame, while they are captured by the basis functions in the modified MSFEM.
Implementation
- Computing the Pressure with MSFEM
- Computing the Streamfunction
- Coarse Interpolation
Like the basis functions of the MSFVM method, this second set of basis functions only needs to be calculated in a preprocessing step. In general, the velocity will not be smooth and the curl calculation will be inaccurate. The only part of the algorithm that contains a calculation on the fine scale is the calculation of S(p, ψ) and ˜v0(p, ψ), which are used to solve the saturation equation.
This is possible for S(p, ψ) by first writing the transformation Jacobian in terms of multiscale basis functions χk of pressure.
Numerical Results
- The Transformation P 0 , Ψ 0 → P, Ψ
- Upscaling Only the Pressure
- Full Upscaling
We have recalculated the pressure four times and compare the improved and refined quantities at one pressure time step before the final time. The pressure and velocity errors should be compared to the velocity change between t = 0 and t= 3Tf inal4. In order not to waste computing resources, the pressure rise error should be similar in magnitude to the saturation rise error.
For example, we can scale up the saturation with S to 50×50 cells and the pressure to 20×20 cells.
Conclusion and Future Directions
- A porous rock
- Staggered grid for the pressure
- Shock and rarefaction of the Buckey Leverett equation
- Fingering in two phase flows
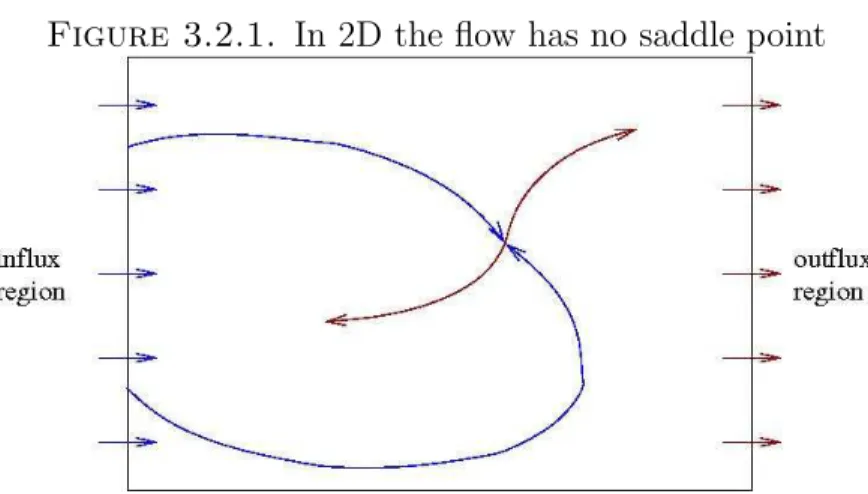
- In 2D the flow has no saddle point
- Velocity profile for shear flow with a fast channel
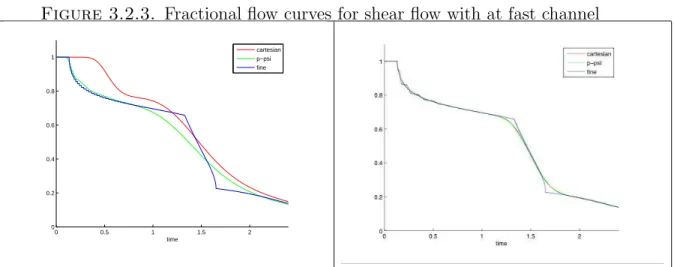
- Fractional flow curves for shear flow with at fast channel
- Moving mesh with slowly varying velocity field
- The mesh transformation
- Moving mesh with rapidly varying velocity field
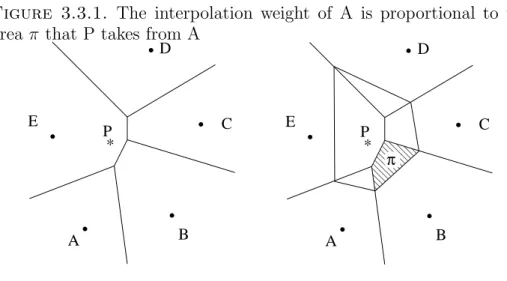
- Interpolation weights for natural neighbor coordinates
- Numerical diffusion in the presence of fast channels
- With a fine grid numerical diffusion is decreased
- Convergence rate of the fine Cartesian and pressure-streamline methods 50
- Fine and coarse characteristics intersect at the boundaries of the cells
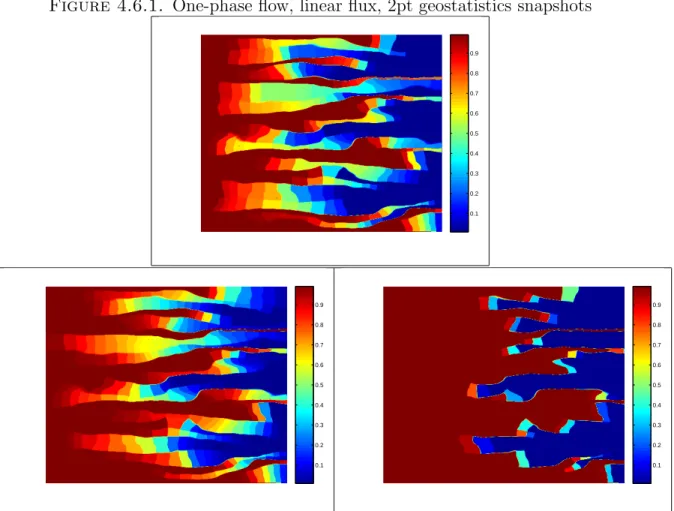
- One-phase flow, linear flux, 2pt geostatistics snapshots
- Saturation snapshots for a layered permeability field, linear flux
- Saturation snapshots for a fast channel (SPE10 36), linear flux
- Saturation snapshots for a layered permeability field, nonlinear flux
- Saturation snapshots for the percolation case (Stanford 44), nonlinear flux 88
- Saturation snapshots with decreasing coarse block size
- Fractional flow rates with decreasing coarse block size
- Boundary conditions for the cells of the pressure equation
- The Multiscale Streamline Method
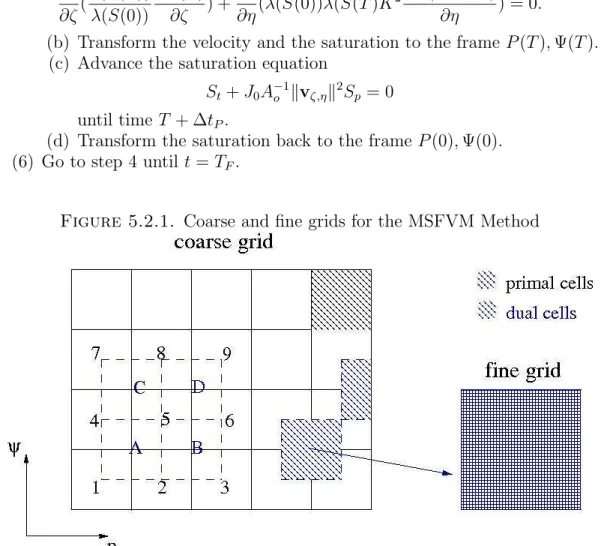
- Coarse and fine grids for the MSFVM Method
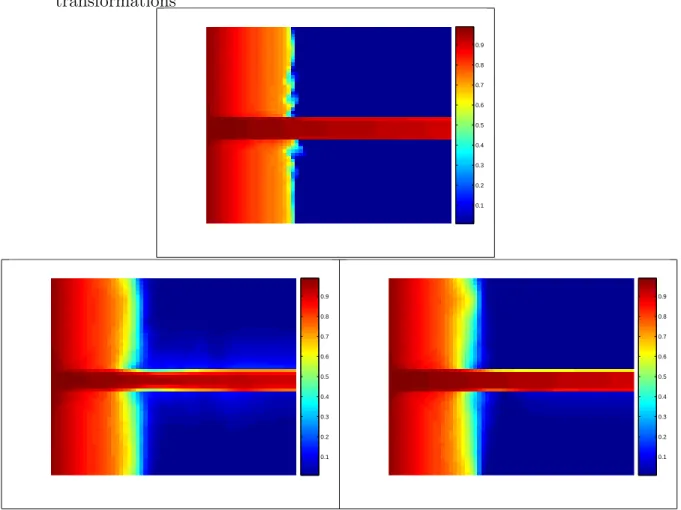
- Cartesian and P 0 , Ψ 0 coordinate transformations
22] Efendiev Y, Ginting V, Hou T, Ewing R, Accurate multiscale finite element methods for two-phase flow simulations, Journal of Computational Physics (submitted 2005). 23] Efendiev Y, Hou TY, Wu X, Convergence of a Nonconforming Multiscale Finite Element Method, SIAM Journal of Numerical Analysis, Vol. 28] Hou TY, Wu XH, A multiscale finite element method for elliptic problems in composite materials and porous media, Journal of Computational Physics, Vol.
33] Jenny P, Lee SH, Tchelepi HA, Multiscale finite volume method for elliptic problems in subsurface flow simulation, Journal of Computational Physics, Vol.