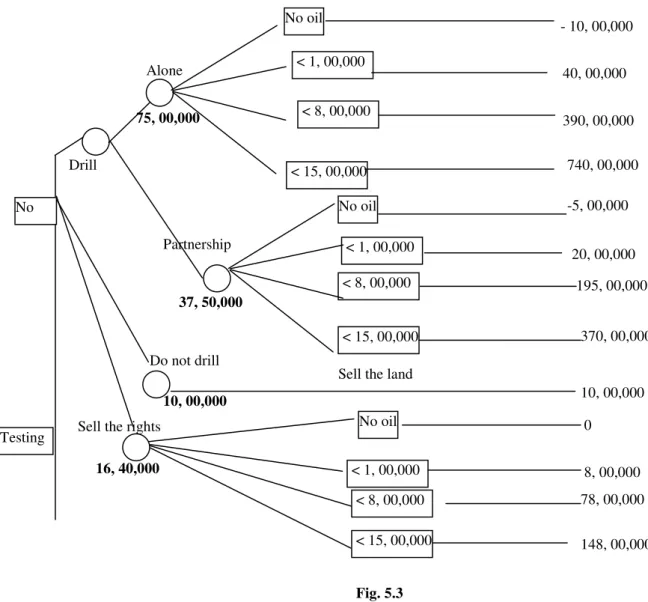
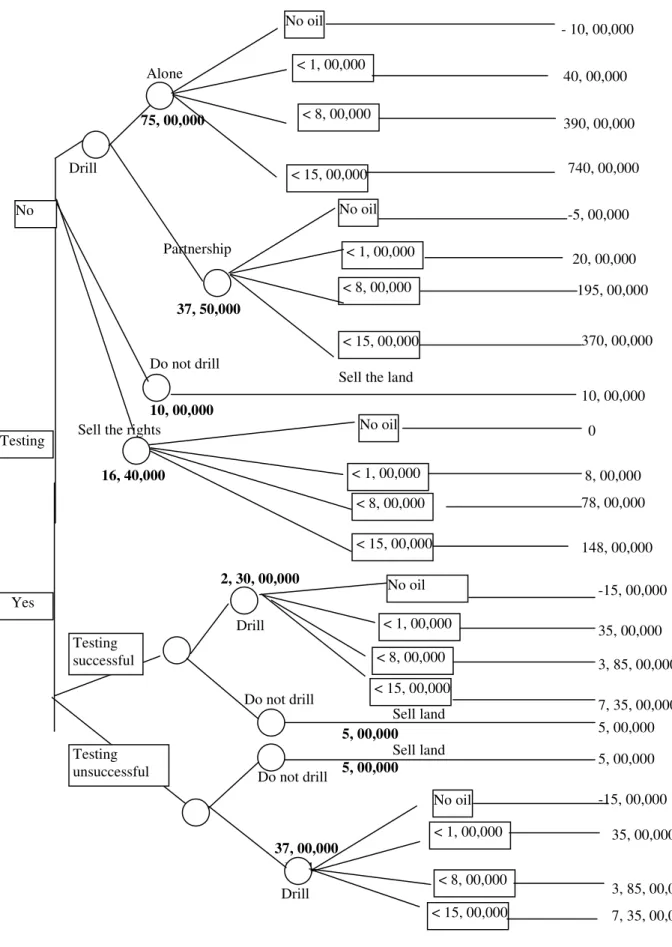
In fact, the company that owns the land has estimated the following states of nature with respective probabilities (without testing):. Since there is a lot of effort that there will be no oil, to reduce the risk, the company can choose a 50% partnership with another company, which will be applicable both in the case of oil and no oil. ii) Sell the drilling rights for 1/5 of the revenue, if any. If the company continues to drill, it must decide whether to do the drilling in partnership or alone.
If the company decides to test, how should it proceed if the tests are successful. If the company decides to drill alone, then it must calculate the yield for the four states of nature and then make a decision. If the company decides to drill in partnership, its profit/loss will be half of what these are if it decides to go it alone.
If the company decides to sell the rights, it will bear no loss, but the profit would be 1/5 of what these were if it had decided to drill. But if the firm decides to sell the land, it will earn a profit of Rs. Similarly, if the company decides to go for testing, the tree can be cut at points if the test is successful or unsuccessful, and decisions can be made.
If the firm decides not to go for testing, it should undertake the drilling alone as this will maximize the expected return. ii).
Some more examples
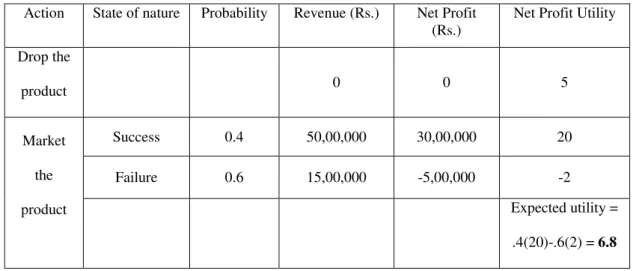
Example 2: Consider the case of a software company that has developed new software to help mathematical researchers develop the theoretical aspects of their research. Most of the software developed so far is useful for analytical purposes, but the proposed software will also be helpful in experiment design and data generation. The company believes that there is a 0.6 probability that the software will be successful in the market.
But since the software development is a time-consuming and expensive task, in case of a failure, the company will have cumulative losses of Rs. It can engage three experts who would use the software on a trial basis and give their opinion on the success of the software in the market. If the software is successful in the market, then the probability that the experts will rate it positively is 0.5.
Sol: The two alternatives for the company are:. ii) Engage experts and follow their opinions; In this case, the expected return depends on the probabilities of success and failure if experts are not involved. However, when the experts are involved, their opinion is a function of the probabilities already estimated by the company, i.e. this is a case of Bayesian estimation.
Thus, if the firm engages experts and they approve the software, it is worth launching it. The optimal policy is that the firm does not need to seek experts and should launch the software on the market. Based on past experience, the company knows that if the drug is successful, it would have an expected gross return to the tune of Rs.50,00,000.
He may introduce the drug on a limited basis in the market to get feedback before launching the drug. If the test market results are successful, the success rate of the drug in the commercial market is revised to 0.75. Since the expected utility of direct product launch is more than the expected utility of test marketing the product, the firm should go for direct product marketing.
Sensitivity analysis
The graph shows that the decision is very sensitive to p, since p = 0 gives a huge loss, but p = 1 gives a huge profit.
An integrated example
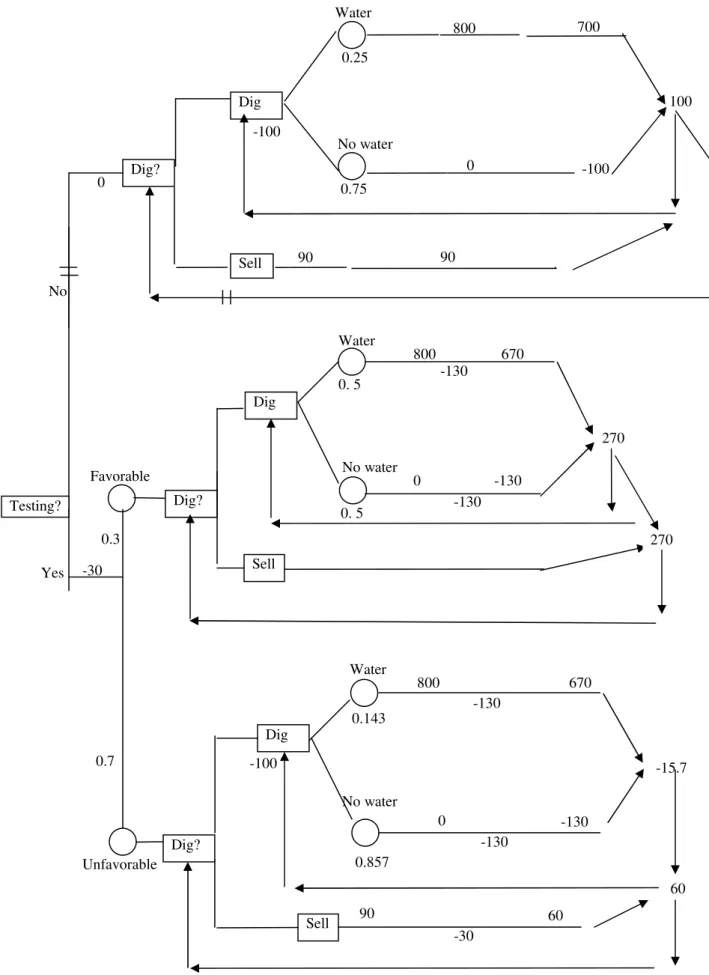
This high cost is due to the fact that the water, if anything, will be several hundred feet below grade, and that several places may have to be dug. Obviously, the expected return from digging is more than the expected return from selling. But Hira is well aware that a statement like "25% chance of finding the water" is very rigid.
If p is the probability of finding water, the expected return from digging is given as. The intersection is the point at which the expected return from digging is the same as the expected return from selling, i.e. according to Hira, the optimal policy should be: i) Keep the land if the results are favorable; and (ii) sell the land if the results are unfavorable.
Technically this means whether the expected value of the sample information is more than the cost of obtaining it or not. Expected reward of testing = (expected payoff | favorable outcome) P(favorable outcome) + (expected reward | unfavorable outcome) P(unfavorable outcome). The policy, then, should be (i) Do the testing. ii) If the results are favorable, dig up the land (iii) If the results are unfavorable, sell the land.
The centre's management has assessed that the annual need for executive hours is as follows. Find the optimal number of copies to order to maximize profit in the store. The company's target rate of return is 10%, above which its utility increases very rapidly.
If the amount the company wants to invest is Rs. a) An indifference between a certain sum of Rs. B). In this investment with probability 0.5 he can lose his money, with probability 0.3 the profit will be 30%, and with probability 0.2 the profit will be 75% of the investment. If the results of limited production are promising, full-fledged production can be undertaken.
There is a 40% chance that market acceptance will be high if full-scale production is carried out. If the limited production results in low market acceptance, the full-scale production will succeed with probability 0.20.