The work in this thesis titled "Soliton Steering and Switching Dynamics in P T-Symetrical Nonlinear Directional Couplings" was performed by me under the supervision of Prof. dr. The works presented in the thesis are entirely my own, unless otherwise stated in the thesis. It is certified that the work in the thesis entitled "Soliton Steering and Switching Dynamics in P T-Symmetric Nonlinear Directional Couplers" by Dipti Kanika Mahato, a student of the Department of Physics, IIT Guwahati, was performed under my supervision and has not been elsewhere submitted for the award of a diploma.
A CKNOWLEDGMENTS
I would like to thank my current batch members, Sampreet, Roson, Puja, Alolika and Urmimala for their wonderful friendship and fun discussions we had about academic and non-academic things. I would like to thank all my classmates of 2016, all seniors and juniors for the camaraderie and positive interactions. I am also indebted to my school friends Saswati, Sriparna, Sucharita and Subhrajit, for their years of trust and friendship.
A BSTRACT
L IST OF P UBLICATIONS
Publications included in the thesis
Other Publications
L IST OF A CRONYMS
L IST OF F IGURES
64 5.5 Effect of TOD on control dynamics of dark soliton inP T-symmetric couplers. a) and (b) represent transmission characteristics in type-1 and type-2 coupling, respectively. 67 5.7 Dark soliton transmissions T1 (green solid curve) and T2 (red solid curve) in the rod and cross channels of π/2 couplers as a function of relative phase of the weak control pulse with power ratio=1. a) Conventional coupling, (b) type-1P T-symmetric coupling and (c) type-2P T-symmetric coupling. 68 5.8 Dark soliton transmissionsT1 (green solid line) and T2 (red solid line) in. bar and cross channels of 3π/2 couplers as a function of relative phase of the weak control pulse with power ratio = 1. a) Conventional coupler, (b ) type-1 P T-symmetric coupling and (c) type-2P T-symmetric coupling.
L IST OF T ABLES
I NTRODUCTION
The topics and aim of research
Therefore, in search of an all-optical switching device with lower critical power, we have played with configurations and system parameters under the effect of P T symmetry, keeping the basic structure as a nonlinear directional coupler. In this thesis, we report our studies on the driving and switching dynamics of solitons within directional nonlinear P-T-symmetric pairs that are briefly discussed below. a) Ultrashort. In this context, a two-core nonlinear directional coupler exhibiting power-dependent switching has been extensively studied [31,32,33].
Outline of the Thesis
It has been previously reported that in the context of conventional intrapulse pairs Raman scattering stabilizes symmetric solitons at sufficiently large energies. However, in the case of the aP T symmetric coupler, we show that a partially radiative soliton induced by high values of gain/loss (although the pulse is the fundamental low-energy soliton) is stabilized in the presence of higher-order perturbations. Bistable solitons in the context of P T -symmetric coupling with saturable nonlinearity are studied.
T HEORETICAL B ACKGROUND
- P T Symmetry
- Understanding P T -Optics via a directional coupler
- Kerr effect
- Nonlinear directional fiber coupler
- Dispersive and Nonlinear Phenomena
- Group Velocity Dispersion and Third-Order Dispersion
- Self-Phase Modulation
- Self-steepening
- Stimulated Raman Scattering
- Nonlinear Schrödinger Equation
- Optical Solitons
- Bright solitons
- Dark solitons
- Bistable solitons
The transition from the continuous to the broken PT regime occurs at the critical value of the coupling parameter, gth=κ (remember εth!). The third-order sensitivity χ(3) represents the cubic response of the medium to the incident light. Since the nonlinear phase shift is proportional to the instantaneous intensity, different parts of the pulse experience different phase shifts.
Changing the maximum input soliton power is not the only way to achieve soliton switching. This dispersive pulse chirp plays the main role in the formation of an optical soliton in the fiber. It leads to asymmetric broadening of the pulse and generates oscillatory structures at the trailing and leading edges of the pulse.
Due to the dependence of the refractive index on the intensity, the mode expansion constant can now be written as The phase shift experienced by an optical beam in propagating through a length L of optical fiber is given by One of the most useful consequences of SSP is the existence of optical solitons in the presence of irregular GVD.
This occurs due to the variations in the relative strength of dispersive and non-linear effects, which depend on the propagation distance.
![Figure 2.2: Optical wave propagation when the system is excited at either waveguide 1 [left panel: (a) and (c)] or waveguide 2 [right panel: (b) and (d)]](https://thumb-ap.123doks.com/thumbv2/azpdfnet/10343301.0/41.892.174.750.169.588/figure-optical-propagation-excited-waveguide-panel-waveguide-right.webp)
U LTRAFAST FEMTOSECOND SOLITON STEERING IN
K ERR P T COUPLERS
- Introduction
- Model: P T -symmetric fiber coupler
- Impact of higher-order nonlinear effects
- Impact of higher-order dispersions
- Combined effect of higher-order perturbations
- Summary
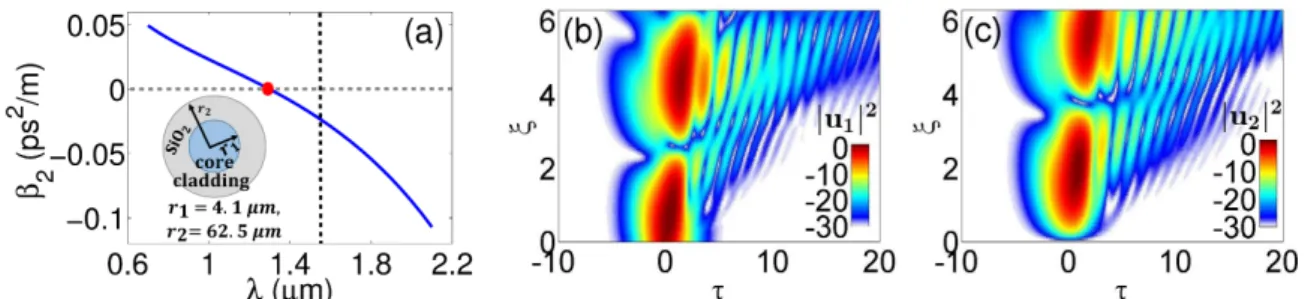
However, in the case of the aPT-symmetric coupler, we show that a partially radiating soliton caused by high gain/loss values (even though the pulse used is a low-energy fundamental soliton) is stabilized in the presence of higher-order perturbations. The system described by Eq. 3.1) is P T-symmetric due to the presence of the equal gain and loss in the two waveguides, which is written in terms of ∓Γ. 3.1) contains all higher-order terms that act as perturbations associated with ultrashort (fs) pulse dynamics [35].
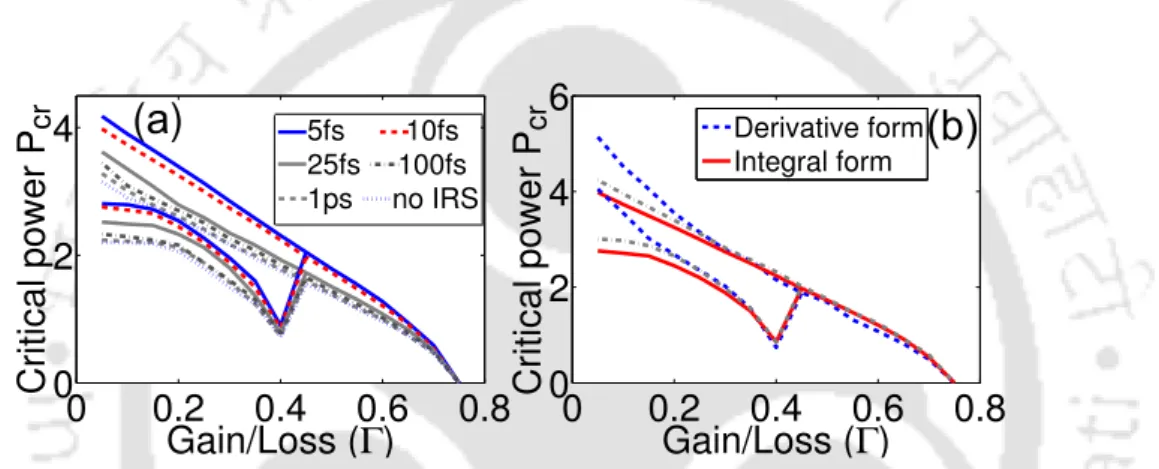
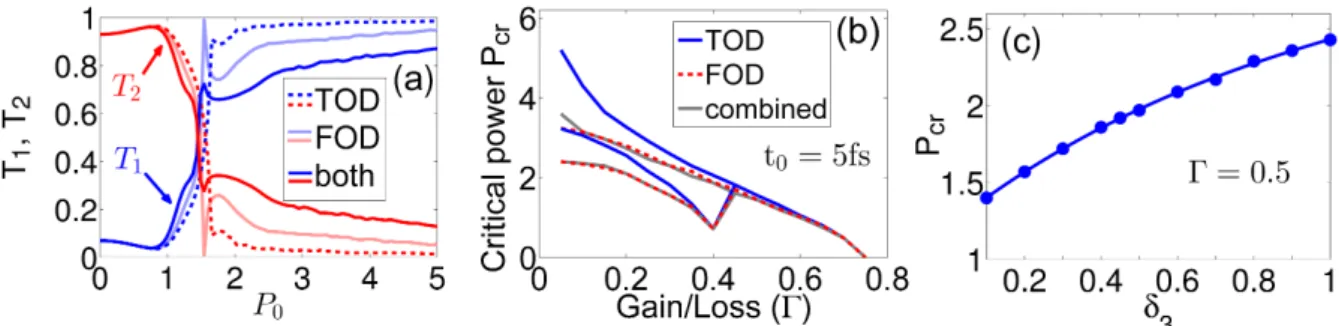
Then we solve the equation numerically. 3.1) taking into account all disturbances present in the system. To investigate the effect of IRS and SS on the soliton steering dynamics in a 2π P T-symmetric fiber coupler, we first numerically solve Eq. (3.1) for a 10 fs input sech pulse in the presence of IRS only. With the increase of the pulse width from t0=5fs to 0=1 ps, the value of the critical switching power decreases significantly, as shown in Figure 3.4(a).
Specifically, the soliton emits energy in the form of dispersive waves (DWs) that produce isolated spectral peaks [35,70,71]. Moving to switching dynamics such as IRS disorder, the critical switching power also changes in the presence of HOD terms. In Figures 3.4 (a) and 3.6 (b) we can also see that considering the t0=5 fs pulse, the critical switching power increases significantly for lower gain/loss values in the presence of HODas compared to higher order nonlinearities.
It shows a similar trend as observed in the cases of individual disturbances [Figures 3.4 (a) and 3.6 (b)].
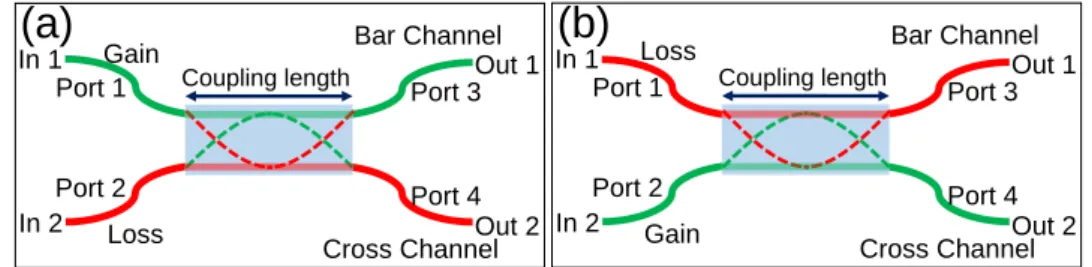
B ISTABLE SOLITON SWITCHING IN SATURABLE NONLINEAR P T COUPLER
- Introduction
- Model and Theory
- Soliton evolution and switching dynamics
- Bistable Soliton dynamics in P T -symmetric saturable coupler
- Power-controlled switching dynamics
- Spatiotemporal Soliton Dynamics
- Switching dynamics by controlling the relative phase
- Summary
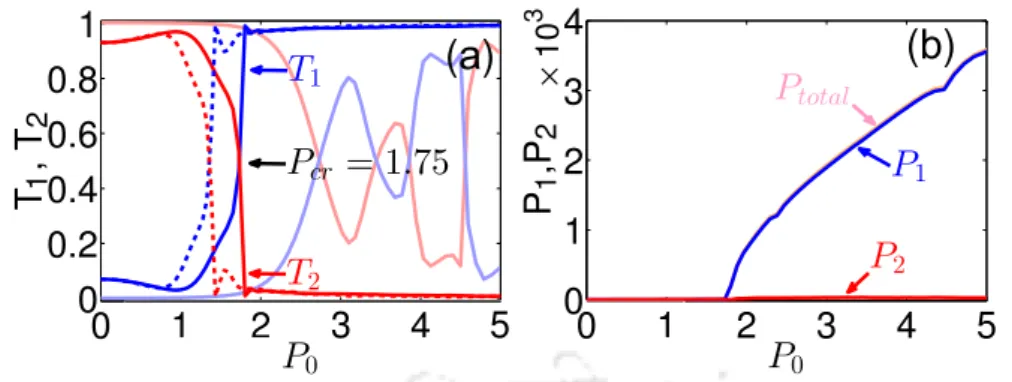
In addition to the input power, the relative phase of the input solitons and the saturation coefficient are additional control parameters that effectively tune the switching dynamics. In our work, we considered =1, which means that the input pulse was triggered at the saturation power at which the nonlinear response of the medium saturates. This plot shows that as Γ approaches singularity (ie Γ = κ = 0.1 in this particular case), no switching occurs, meaning that regardless of the input power, all the power remains in the launch channel.
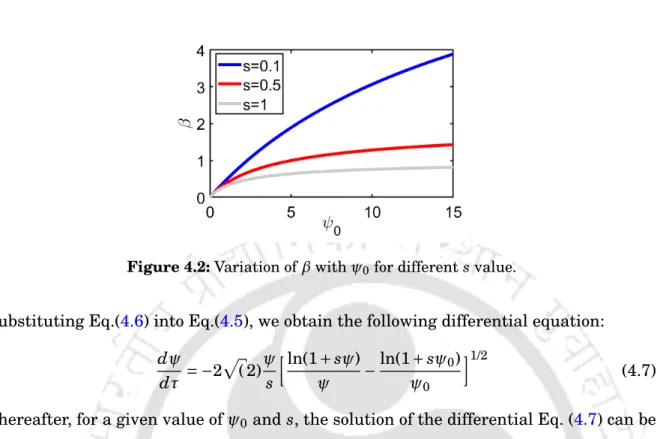
Next, the switching dynamics of the individual bistable solitons obtained in Fig.4.5(d) are investigated in Fig.4.6(a) and 4.6(b). The critical force of switching corresponding to the pulse with ψ0=2.87 is lower than that of the pulse with ψ0=0.47. Next, we study the role of the strength of SN, s for the same two couplers in the weaker coupling regime by setting κ=0.1, shown in Fig.4.7(c) and4.7(d).
In this section, we illustrate the dynamics of the spatiotemporal evolution of a soliton inside two cores of two SNCs. However, for the aP T-symmetric SNC case, we observe that the soliton power comes from the second channel, as shown in Figures 4.9 (c) and 4.9 (d)]. In addition to power-controlled switching, for the completeness of the study, in this section, we investigate phase-sensitive switching dynamics as another type of all-optical switching device.
We also plot the effect of the strength of SN on the phased switching dynamics considering the previous set of values as in the case of power control.
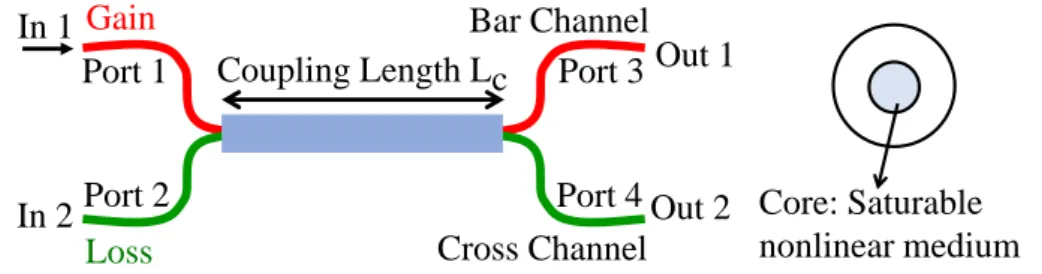
D ARK SOLITON STEERING IN K ERR P T COUPLER WITH DISPERSIVE PERTURBATION
- Introduction
- Theoretical Model
- Results and Discussions
- Effect of TOD
- Effect of IMD
- Phase-controlled switching
- Summary
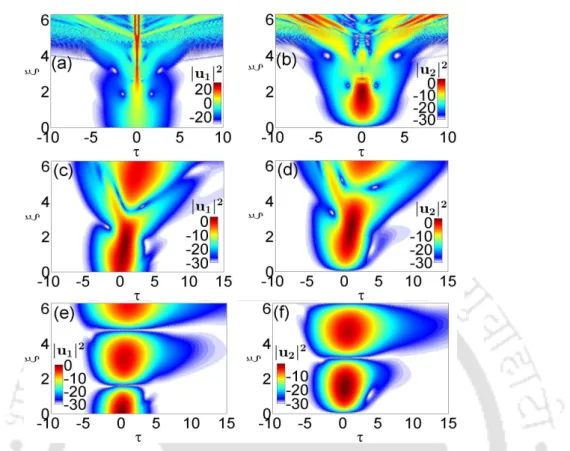
In coupled state theory, this group delay between the states is analogous to the coupling coefficient dispersion. Ψ2(Lc,τ)|2dτ are the output powers of the transmitted pulse in ports 3 and 4 of the coupler. From Fig.5.3(c) it can be clearly seen that the critical power is reduced to Pcr=1.25 with an excellent transmission efficiency for a type-1P T-symmetric coupler compared to the unwanted oscillation in the conventional [see fig. 5.3(a)].
Also, for the type-1P T-balanced coupling, the gain of the output pulse intensity above the critical power is more than a factor of 5 times the output pulse in the type-2 coupling [Figures 5.3(d) and 5.3(F)]. However, for a type-2 coupling we observe a different dynamic, where the critical power decreases linearly with an increase of the gain/loss parameter to the value Γ=0.4. Here, for the type-2P T-symmetric coupling, a significant difference in the transmission characteristics is observed for Lc=π/2 and 2π.
However, for a 2P-type T-symmetric coupler with first waveguide loss, it was shown in Fig. 5.6(b) that IMD has no effect on the critical power for dark soliton switching, although it shows a smaller effect in the nonlinear regime above the critical power. Here we note that increasing the coupling length results in an extremely sharp switch to the rod state for a wide range of φ. For a 1P-type T-symmetric coupler as shown in Figure 5.10(b), an increase in the intensity ratio r results in a decrease in the transmission efficiency at output port 3 when φ=360◦.
For a type-2P T-symmetric coupler as illustrated in the right two panels, Fig.5.12(a), the input soliton is launched at port 1.
C ONCLUSION
The corresponding theoretical model together with a discussion on the numerical finding of soliton solution that can propagate in a saturable nonlinear medium has been demonstrated. The spatiotemporal characteristics of solitons are illustrated and the phase-controlled soliton switching behavior is demonstrated. Furthermore, we studied the switching dynamics of the dark soliton by controlling the phase of a weaker signal in P T couplers with two different coupling lengths and illustrating its advantage over the power-controlled one.
As a potential future work, one can look for the development of some analytical methods, especially the so-called variational methods in the context of P T-symmetric coupled systems. This will enable more insights into the operation of various soliton parameters in the system. In the present thesis, we have restricted ourselves to second-order exceptional points (EP2s). EPs are widely referred to as the branch point singularities at which both the eigenspectra and the associated eigenvectors corresponding to a nonconservative physical system merge.
Since the system undergoes a phase transition manifested by the sudden change in its behavioral dynamics around the critical points, systems exhibiting P T symmetry have attracted great interest in recent years. The first experimental investigation of EP3 in a ternary P T-symmetric resonators was demonstrated by observing the cubic root dependence of the frequency distribution on the applied external disturbance in the refractive index of the system [107]. The idea of introducing a neutral resonator between the gain and the loss resonators paved the way to use such a coupled system in other optical systems such as atomic physics, optomechanics and photonic crystals.
One of the extremely fruitful research efforts would be to perform an investigation of the soliton dynamics in a three-core T-symmetric NLDC.
B IBLIOGRAPHY
Malomed, "Stability limit and collisions of two-dimensional solitons in P T couplers with the cubic-quintic nonlinearity," Phys. Kumar, “A comparative numerical study of soliton switching in a nonlinear directional coupler with saturating nonlinearity,” Opt. Li, “Gap solitons supported by parity-time-symmetric optical gratings with defocus saturable nonlinearity,” Opt.
Li, “Multihump solitons in two-dimensional parity-time-symmetric optical gratings with focusing saturable nonlinearity,” The European Physical Journal D. Dark soliton switching in a NLDC in the presence of higher-order perturbative effects,” Opt. Porsezian, “ Modulational instability in a twin-core fiber with the effect of saturated nonlinear response and coupling coefficient dispersion,” Phys.
Sarma, “Dark soliton switching in NLDCs in the presence of higher-order perturbative effects,” Opt.
V ITA