LANGUAGES, STRUCTURES, AND MODELS OF

One of the postulates (the Projection Postulate) states that “[i]f we perform the measurement of [A] and that . The elements we consider in the structure, outside the domain(s) are primitive elements of the structure, and here we will assume that the structures contain only relations (across the domain).

Figure 3.1: A general simplified schema for physical theories showing di ff erent senses of the word ‘model’

Informal semantics of L ∈

To begin with, let's reproduce here some examples of possible interpretations for L∈.5. The first interpretation takes D as the set Z of the integers, and ξ as the relation < on the integers. Franco de Oliveira gives us yet another example, concerning the axiom of the disordered pair. Important to remember that there are two notions of consistency, one syntactic and the other 'semantic'; the syntactic definition says that a theory T, whose language contains a negation symbol ¬, is consistent if there is no formula α such that both α and ¬α are propositions of T.

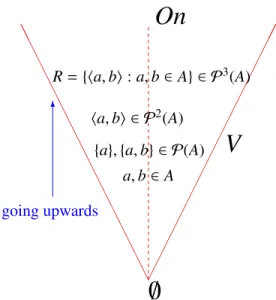
7By recursive enumeration, we intuitively mean that there is an algorithm (a computer program) that can in principle enumerate all the axioms of the theory, but not the sentences that are not axioms. that is, 2ℵα = ℵα+1 for any ordinal α).8 The technique of constructing internal models became one of the important tools of mathematical logic, but we are not concerned with them here, although we shall see later what it means to say that the axioms of ZF are true in an inner model M; it suffices to emphasize that ZF has 'models' (if consistent) and that these models are not ZF sets. 10 Let M be a class (it can be a set) and an Fa formula for L∈. The formula FM is called derelativization of FtoMif it is obtained by substituting ∃x∈ Mfor∃x and∀x∈ Mfor∀x. This can be intuitively understood because the set of two objects is at a higher level than the levels of the objects. iii).

Figure 5.1: The well-founded ‘model’ of ZFC without ur-elements.

The di ff erent ‘models’ of ZF

But in such a countable 'model', the set that (in the 'model') corresponds to the set of real numbers must be countable. The above structures for fields and vector spaces are order-1 structures, because their relations only have elements of the domains as relata. Thus, order-1 structures (such as those treated by model theory) consider only order-1 relations, that is, those that have only the elements of the domain, but not its subsets, as relations.

More sophisticated structures needed to deal with empirical sciences (and mathematics) are not order-1 in this sense. In particular (let us emphasize this), the above definitions show that we can consider order-n (n > 1) structures within the framework of first-order languages. As noted by da Costa and Rodrigues [op.cit.], the usual mathematical structures can be reduced to structures embedded in this scheme, but sometimes this can be very difficult.

Figure 6.1: The well-founded ‘model’ V = h V, ∈i of ZF, a structure built within ZF, and the scale based on the domain D

Languages

Remember that the expression 'universal algebra' comes from Whitehead's book (from 1898) Universal Algebra, which means, roughly, the study of algebraic structures (or algebras - see below) from a general ('universal'). ) point of view, which departs from the study or particular algebraic systems.

Algebras

AsubalgebraofA is an algebraB = hB, fλ0i such that B ⊆ A and the fλ0 are the restrictions of the corresponding fλ to B. But this does not happen if we describe a group by mentioning all the basic operations, namely asG = hG,∗ ,¯,ei, where ¯ is a unary operation on G which for every a ∈ G has its inverse ¯a ∈ G associate and e is the identity element of the group. Any algebra has a type agreement, or signature (please do not confuse with the concept of type given previously).

By considering the rank of the operations involved, we can say that this structure has a type of equality (2,2,0,0). Similarly, the structure N = hω, s,0,+,×i for elementary arithmetic has a similarity that only the order of the operations is mentioned. If h is bijective, it is called an isomorphism, and in this case we write A ≡ B.

Languages as free algebras

This second set plays the role of the algebra operations we will define. In our example, atomic formulas are propositional variables and expressions of both forms ¬pi and → pipj.

Languages for speaking of structures

The language of a structure

Definability and expressive elements

If we aim to define the subset relation ⊆, we can do so in the extended language L∈∪{⊆. If we consider a suitable infinitive language, e.g. Lω1ω (where we can allow countless infinite conjunctions and disjunctions), we can within the parentheses the formula we abbreviate with. We know that within ZFC (supposedly consistent), the set R of reals is not countable.

But if we use a suitable infinitive language Lµκ (for suitable ordinals µ and κ), we can find a name for each rule, so that we can define all of them according to the condition given in definition (6.6.2). Using the axiom of choice, we can show that every set is well ordered (by the way, let us insist, this sentence is equivalent to the axiom of choice). According to the axiom of choice, we can assume that this order does exist, since its existence is consistent with ZFC (assumed consistent).

On the new symbols

In other words, no new theorem can be derived that has not been previously proved and is expressed only in terms of primitive symbols and already defined symbols. The new symbol ⊆ is not part of the language L∈−, but belongs to its metalanguage, and the expression A ⊆ B simply abbreviates the sentence L∈−, namely ∀x(x ∈ A → x ∈ B). But there are real numbers that cannot be named even in this way, as we saw above when we discussed the proper order of the real numbers.

For now, what matters is that this function cannot be factorized, giving a particular description of the electrons. This shows that in set theories such as the ones we assume here (and which are assumed in the standard literature), there are no relations without relata, that is, 'pure' relations as THV proponents desire. . A slogan for FSR would read as saying that everything we know in science is through structures, that is, in order to understand, we elaborate conceptual networks around our descriptions of the world by means of (in principle) mathematical structures. that save appearances or, as we prefer to say, which are almost true (da Costa & French 2003).

Figure 7.1: In ZF, the relations on a set A are con- con-structed from the elements of A going upwards in the hierarchy.

Leaving the classical frameworks

These non-Cantorian set theories (Cohen's words) are today quite common in discussions involving set theory proper, but they are still far from the interest of the general philosopher of science. In the Hilbert space L2(R) of the equivalence classes of quadratic integrable functions are the unbounded operators. One of the fundamental theorems of quantum mechanics is Gleason's theorem (it doesn't matter for us to formulate it here).

But before that, let's make a few comments about the nature of the 'models' of ZFC. Leibniz's Principle of the Identity of Indiscernibles (henceforth, PII) plays an important role in the contemporary philosophy of physics. The fact that quantum entities can be indistinguishable is against the thesis that there are no indistinguishable objects, which is the essence of the principle.

Quasi-set theory

Language and basic definitions

The Q theory is based on ZFU-like axioms, but includes two kinds of ur elements and not just one, as in standard ZFU. So, unlike what happens in ZF, in defining such structures we would be able to discuss quantum theories that consider invisible objects that are indistinguishable even outside the structures considered. The concept of quasi-cardinal is considered primitive since it cannot be defined in the usual way (that is, as definite ordinal numbers).

This fits the idea that quantum particles cannot be ordered or counted, but only aggregate in specific quantities. Nevertheless, given the notion of quasi-cardinal, it makes sense to say that there may exist a certain amount of m-atoms that obey certain conditions, even if they cannot be named or labeled. Onis the class of ordinals, defined in the 'classical' part of the theory (back), and there are two kinds of ur-elements.

Figure 8.2: The Quasi-Set Universe. On is the class of ordinals, defined in the ‘classical’ part of the theory (in back), and there are two kinds of ur-elements.

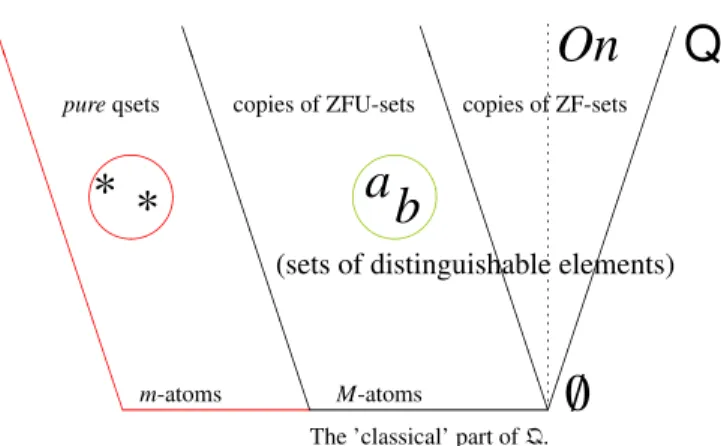
Specific postulates

That is, sets in Q are those entities obtained in the "classical" part of the theory (see again Figure 8-2). 6) ∀x∀y∃Qz(x ∈ z ∧ y ∈ z) Usually (that is, in ZF) we formulate the axiom in an equivalent way, saying that given two individuals a and b, there exists a set containing them are both elements and nothing else. But from the division scheme, using the formula α(w) ↔ w ≡ x ∨ w ≡ y, we get a subqset of z that we denote [x,y]z, which is the qset of the indistinguishable values of x or y belonging to z. Anyway, we can reason informally as if the element of the strong singleton is [[x]]z x, although this should be taken as a figure of speech.

Perhaps a better way to refer to this situation is (informally) to say that the element [[x]]z is an object of type x. As mentioned above, we use only one type of variable, as we believe we can avoid some of the problems that can arise from this option. Of course, this definition could. generalize, taking x and y from observable qsets, but this most restricted axiom seems to suffice for all applications of the theory.).

Quasi-relations and quasi-functions . 126

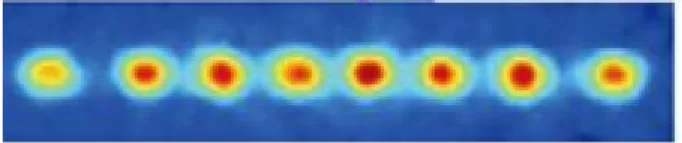
This means that the domain of a q-function does not have two indistinguishable subsets that are mapped into the same qset of the opposite domain. In terms of quantum objects, physicists have used certain 'queues' of calcium ions to transmit information (see Figure 8.3 below), and the information is, of course, independent of the position of particular calcium ions. For whatever reasons, the order of the ions does not matter, and any "permuted" arrangement works the same way.

8In the presence of the axiom of choice, the cardinal of a set A is the smallest ordinal number α such that there is a bijection between A and α. Hence, in quasi-set theory, the concept of quasi-cardinal is taken as primitive, subject to adequate postulates that confer the operational character of the concept. 9This has a clear meaning, since 'numerical diversity' or 'countability' can be regarded as indicators of individuality; yet quasi-sets of non-individual objects can also be considered 'countable' in this sense.

Figure 8.3: Eight Calcium ions in a ‘W state’. (From Scientific American, Mach 2006).

Weak extensionality

A chemical substance such as C2H6O can have the origin of various chemical compounds, which are described by presenting their structural formulas; depending on the arrangement of atoms (their structure or shape), the same accumulation of carbons, hydrogens and. So there is a 'relation' which can be said to be independent of the individual relations it links (except in what respect their 'nature' - see below). Indeed, each oxygen atom of the ozone molecule plays the same role in the reaction.

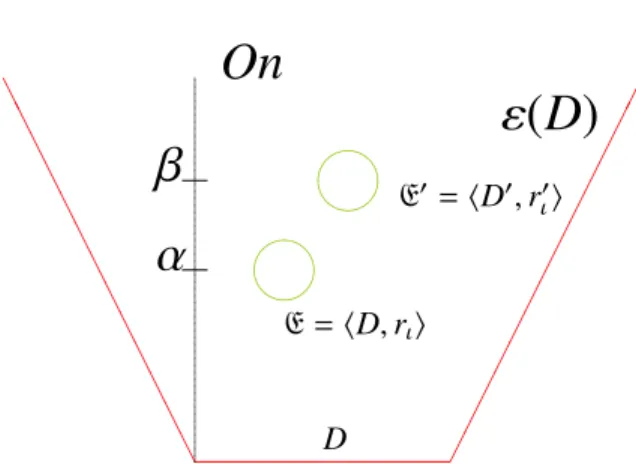
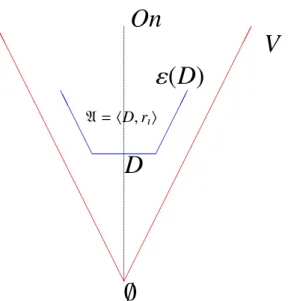
Let's look again at the structure A = hD,rıi built in the 'pure' part of the quasi-set theory (see again the figure 8.5). Jacquette (ed.) Philosophy of Logic, Vol.5 of D.M.Gabbay, P.Thagard and J.Woods (eds.), Handbook of the Philosophy of Science, pp. 1987, A Formalization of Set Theory without Variables, American Mathematical Society. 1981, The Investigation of the Physical World, Cambridge: Cambridge Un. 1980, The Scientific Image, Oxford, Clarendon Press.