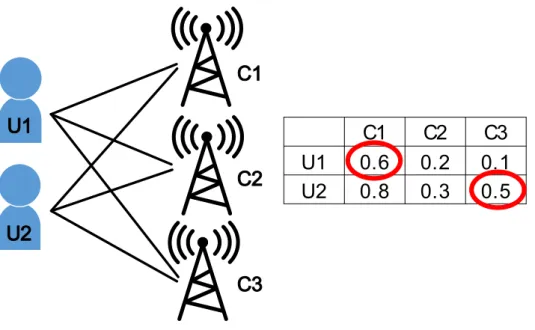
In this paper, we address the user channel allocation problem in multi-user multi-channel CRNs without prior knowledge of channel statistics. Each user either explores a channel to learn the channel statistics or exploits the channel with the highest expected reward based on information collected so far. We consider multi-user multi-channel CRNs where channels are orthogonal and independent of each other.
We assume a time-slotted system where each user can access at most one channel at a time. In multi-user scenarios where multiple users access channels at the same time, a channel should be accessed by only one user at a time due to a collision. This multi-user scenario can be formulated as combinatorial MAB problems [8-16], where the total reward received from playing multiple arms is either the sum of rewards from arms played (linear rewards) or a function of reward vector (non-linear) rewards ).
In this paper, we study the multi-user MAB problem where reward statistics are different for each user-channel pair. We develop low-complexity learning algorithms for opportunistic spectrum access in multi-user multi-channel cognitive radio networks. We assume a time slotted system where each user can access at most one channel in a time slot.
Uniform sampling algorithm
Let a∗ denote an optimal matching (i.e. a maximally weighted matching inG) with expected rewards µi,k as weights on edges such that. We consider regret as the difference between the total reward of an optimal matching and that of the non-optimal matching. It is known that the logarithmic growth of expected regret over time is asymptotically optimal [8].
In this section, we develop the low-complexity learning algorithm which can be applied to more general graph combinatorial MAB as well as bipartite graph. We first describe our low-complexity scheme and then evaluate the performance of our proposed scheme and show that it is asymptotically optimal. It is known that, in a single user scenario (N = 1), if the user plays the channel with the highest UCB index value in each time slot, the regret increases logarithmically with respect to time [5].
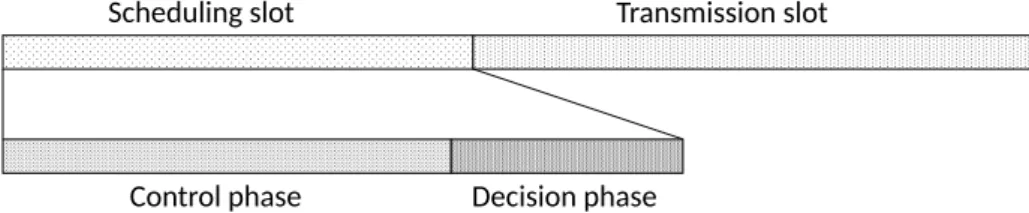
Under multi-user scenarios, finding the maximum weighted match with UCB indices in each time slot achieves asymptotic optimality, which, however, has high-order computational complexity [14]. We address the problem by developing a linear complexity algorithm that guarantees logarithmically increasing regret. A time slot is divided into a scheduling slot and a transmission slot, and the scheduling slot is further divided into a control phase and a decision phase as shown in Fig.
In the checking phase (lines 1 of Algorithm 1), we randomly select a matchm(t)∈ uniformly, which is called a candidate match. In the decision phase (line 2-3 of Algorithm 1), we calculate the sum of the selected UCB indices from the candidate matching m(t) and that of the previous plan x(t−1), and select the one with higher as schedule of rix(t). While the procedure appears to be similar to that of Q-CSMA [17], we aim to minimize accumulated regret rather than queue stability and develop new techniques to evaluate its performance.
In the decision phase, each user calculates the UCB indices for at most two channels: one in candidate matching and/or one in the previous schedule, which can run in parallel and take O(1) time. The idea of reducing complexity in uniform sampling can be applied to other MAB problems, such as a combinatorial MAB with a more general graph instead of a bipartite graph.
Performance evaluation
Let ∆∗min := mina6=a∗∆∗aand∆∗max:= maxa6=a∗∆∗a denote the minimum and maximum non-optimality gap, respectively. Proposition 1 Under uniform sampling, the expected number of explorations to non-optimal matches is upper bounded than . Hoeffding bound [20], the probability that each case of 1) and 2) occurs at time slot can be bounded by N t−2.
We show that, as non-optimal matchinga is planned more often (i.e. a is sufficiently explored), the matching a satisfies V(a;I(t))< V(a∗;I(t)) with high probability, and the probability thatx(t) =a∗ approaches 1. We first show that the probability of underestimating optimal matchinga∗ or overestimating non-optimal matchinga decreases. Non-optimal matching a is scheduled for τˆa(t) ≥l, which implies that each edge (i, ai) satisfies τˆi,ai(t)≥l for all i.
Again, we note that the probability of each event Ai and Bi can be bounded by the Chernoff-Hoeffding limit [20]. We now show that the number of explorations with suboptimal matching is bounded and we have the proposition. We divide the set of all Minto matches into the set of nonoptimal matches denoted by Mo and the set of optimal matches denoted by M∗, i.e., M=Mo∪ M∗.
For an, let ln,m denote the number of time windows that an is scheduled in (Tm−1, Tm], as shown in Fig. 7) In the last equality, the first term denotes the total number of schedules for non-optimal matching up to l, which can be obtained by summing ln,m of black arrows in fig. The second term denotes the total number of time slots that each non-optimal matching is scheduled after it is sufficiently scheduled, indicated by blue arrows in Fig. The second term can be delimited by the maximum number of time slots that matchinga∈S(Tn) can be played during (Tn, Tn+1).
Let {a1,a2, ..,a|S|} denote the set of non-optimal matches that are sufficiently scheduled with τˆan(T) ≥ l, and let Tn denote the time at which matching is a sufficiently scheduled, τˆan(Tn) ) = l.
![Figure 3: Matching a n is scheduled l n,m times during (T m−1 , T m ].](https://thumb-ap.123doks.com/thumbv2/123dokinfo/10522699.0/19.892.137.761.138.409/figure-3-matching-n-scheduled-times-t-t.webp)
Greedy algorithm
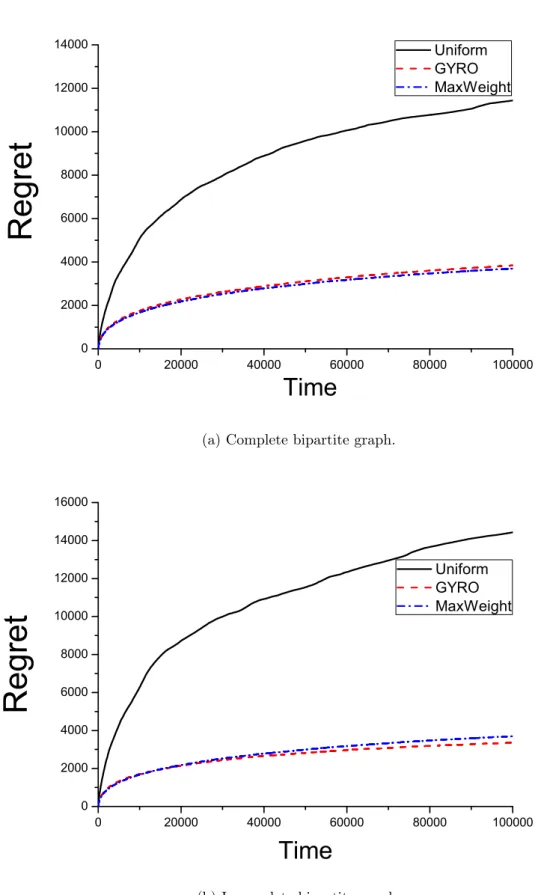
We evaluate the performance of our proposed scheme, and show that it also achieves asymptotic optimality with respect to time. Proof: We assume without loss of generality that the graph is symmetric complete bipartite graph with N =K. For non-symmetric or incomplete bipartite graphs, we can construct such a graph by adding additional users and by setting zero weight on originally non-existent edges.
Suppose S1 is empty, ie. no user broadcasts his best channel in the optimal match G. Since no user broadcasts his best channel, each user has exactly two edges (one with a non-negative weight and one with a non-positive weight) . A cycle must have a negative weight sum because the sum of each user's incoming and outgoing edges is always less than or equal to zero.
Proof of Lemma 3: We prove the lemma by constructing an order o∗ given an optimal matching a∗. According to Lemma 4, S1 is not empty and we let the users in S1 get the earliest order. Note that the order within S1 is not important under our greedy algorithm, as each user will choose a different channel in a∗.
Let G denote the (bipartite) subgraph obtained by excluding all users in S1 and all assigned channels and corresponding edges. Note that the induced matching a∗|Gs is also an optimal matching in subgraph Gs (otherwise we can easily show that a∗ is not optimal inG), and from Lemma 4 we can establish that S10 is not empty either. We let the users in S10 be in the group with the next earliest order.
Using Lemma 3, we can find the optimal match by exhaustive ordering search. If we find the order∗ with the maximum value functiono∗∈arg maxo∈OV(greedyµ(o);µ), we can get the optimal match a∗ =greedyµ(o∗).
Greedy algorithm in randomized orders
Then graph G0 has the same number of vertices and edges of 2N and there exists at least one alternating cycle C [21]. In the control phase, each user calculates UCB indices for all channels in parallel, which takes O(K) time. A central agent collects the indices, which takes O(N) times, and uniformly randomly selects an order.
Performance evaluation
In ao = greedy µ(o), at least one of the actual resources is underestimated, where a o wins in the greedy equation, 2) ina, at least one of the actual resources is overestimated, and 3) requires a non-greedy matching are examined (i.e. a given index increases excessively). Based on the Chernoff-Hoeffding bound [20], the probability that each case of 1) and 2) occurs at time slot t can be bounded by N t−2. We omit its proof because it can be shown in the same way as the proof of Lemma 5. We omit its proof because it can be shown in the same way as the proof of Lemma 3.
Note that the probability of events Ai and Bi can be bounded by the Chernoff-Hoeffding limit [20] as,. Proof of Proposition 2: The procedure to show the proposition is the same as the proof of Proposition 1, except for obtaining the limit of (10). This difference comes from the way of selecting a candidate match under uniform sampling and GYRO.
The inequality can be expanded recursively as in the proof of Proposition 1 except lettingA:= 1 + N!1. We have shown that under our uniform sampling and GYRO algorithms, the expected regret increases logarithmically with respect to time. MaxWeight can be implemented using brute-force search or the Hungarian algorithm [22], whose computational complexity is O(KN) and O((N +K)3), respectively.
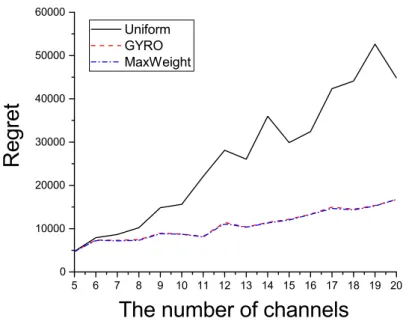
Now we show that the performance differences between uniform sampling and GYRO become larger with respect to the size of the network. The idea of reducing complexity can be applied to other learning problems and remains a future work. Shroff, “Pricing for Past Channel State Information in Multi-Channel Cognitive Radio Networks,” IEEE Transactions on Mobile Computing (TMC), forthcoming.
Walrand, "Asymptotically efficient allocation rules for the multi-armed multi-play bandit problem - Part I: IID rewards," IEEE Transactions on Automatic Control, vol. Swami, "Distributed algorithms for learning and cognitive media access with logarithmic regret," IEEE Journal on Selected Areas in Communications, vol. Srikant, "Q-csma: Queue length-based csma/ca algorithms for achieving maximum throughput and low delay in wireless networks," IEEE/ACM Transactions on Networking (ToN), vol.
Choi, et al., “Dss: Distributed sinr-based scheduling algorithm for multihop wireless networks,” IEEE Transactions on Mobile Computing (TMC), vol.