The monocular cameras can be used in the vehicle platoon systems to determine the distance to a vehicle in front. It locates the number plate of the leading vehicle in the moving object area after removing the background.
Introduction
- Research Background and Objectives
- Related Works
- Moving Objects Detection
- Vehicle Distance Measurement
- Consensus Control
- Containment Control
- Thesis Contributions
- Main Contents and Organization
The consensus control is one of the basic problems of cooperative control of multi-agent systems. In [23], the texture feature of the license plate area is used for license plate detection.
Moving Object Detection
- Motion Compensation
- Background Modeling
- Background Subtraction
- Experiment Results
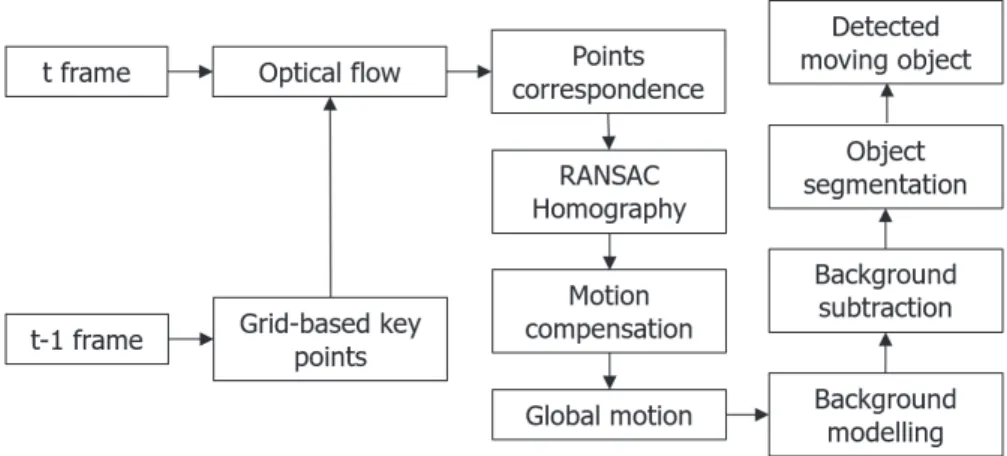
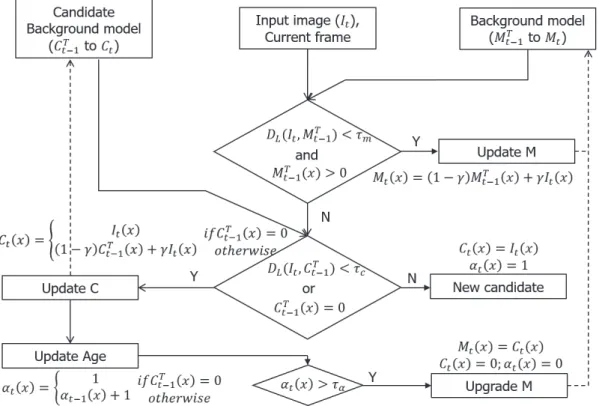
The number of key points is based on the accuracy of the homography matrix and the speed of calculation. After the frames are aligned, part of the moving object in the scene can be shown by the frame difference between the two frames. The background pixels in the candidate background model and the background model are set to uninitialized.
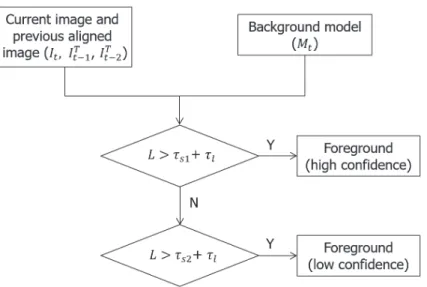
The homography matrix Ht1 can be calculated by pyramidal Lucas-Kanade optical flow based on the keypoint of the current frame and the previous frame. Then, the background model and candidate background model are transferred from the previous frame to the current frame and updated by the background modeling strategy. The example of the comparison for no adaptive threshold and using adaptive threshold is shown in Figure 2.6 and Figure 2.7.
Using the two previous homography matrices (Ht1 and Ht2), the previous two frames are aligned with the current frame. The shadow region has no illumination, its pixel change values between the current frame and the background model are generally locally consistent. The result shows that the right area of the background model is black, this area is not available due to the moving camera.

Vehicle Distance Measurement
License Plate Detection
The Sobel operator is used to calculate the vertical texture of the vehicle grayscale image. So a grayscale image is obtained that only preserves the texture in the vertical direction of the vehicle. Due to the influence of the lighting, the brightness between the number plates is very different.
This method can ignore the shadows on the license plate and ultimately preserve the texture in the vertical direction of the vehicle. In order to find the contour of the license plate, all textures must be connected to each other in the license plate area. After the closing operation, the white license plate area textures are connected to each other to form a white license plate area.
Some filter conditions are set to find the outline of the white area and locate the license plate. In the vehicle image, the license plate must be in the center position area of the image. a) Closure (b). This method locates the license plate according to the texture of the license plate area.

Vehicle Distance Estimator
It can make the texture contour in the image smoother and eliminate the independent and thin texture. This method would not be effective under different conditions, such as resizing the license plate, removing the license plate, or placing the license plate in an atypical orientation. The height and width of the plate in pixels in addition to the pixel position of the license plate can be used to estimate the distance from the vehicle in front.
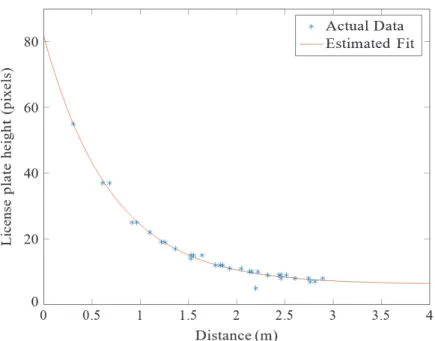
The license plate is expected to be visible and within camera range. As the distance to the object increases, the observed size of the object decreases exponentially. In this method, the observed height of the license plate H in the image decreases exponentially with the distance L between the vehicles.
The perceived number plate height is used because the perceived number plate width can vary depending on the heading of the front vehicle, but the perceived height remains relatively constant with variations in the front vehicle heading. H aebLc (3.7) Therefore, the leading vehicle distance is estimated from the observed license plate height using the logarithmic equation with three fixed parameters. The license plate was tracked and the distances were recorded at various angles (0 rad, π/2 rad) and distances (0.3 m, 3 m) from the camera.
Vehicle Platoon Modeling
Node dynamic
Considering the complexity and accuracy of the modeling, the longitudinal dynamics of the vehicle is simplified and the following models can be obtained. Considering the vehicle as a mass point, the dual integrator model is used to describe the nodal dynamics. 4.1) If the vehicle group is considered as a mass-spring-damping system [84][85], a linear second-order model description is obtained.
For theoretical analysis, a single integrator model is used to approximate the dynamics of a vehicle node [86][87]. In this model, the control input is equivalently converted to motor torque or braking torque. A single-input single-output model is often used in the study of queuing stability in the frequency domain.
Information Flow Topology
Graph theory plays an important role in describing information communication between multi-agent vehicle platoon systems. A graph consists of a set of vertices and a set of edges representing each agent and each directed flow of information. The adjacency matrix 𝒜 𝑎 ∈ 𝑅 is defined as 𝑎 1 if there is a directed path from agent 𝑖 to agent 𝑗; otherwise 𝑎 0.
Indicates a group of vehicles which information can be detected from node 𝑖 to the following vehicle. In this paper, it is assumed that the graph contains a directed spanning tree and the root agent can obtain the leader information. The adjacency matrix associated with the leader is defined by 𝒜 the diagnostics 𝑎 , ⋯ , 𝑎 , where 𝑎 1 if and only if the follower 𝑖 can obtain the leader's information;.
Vehicle Platoon Geometry Modeling
The expected distance between two adjacent vehicles is independent of the vehicle speed, which means that a higher traffic density can be achieved. For a constant headway time in the vehicle platoon, di1,i is a linear function of the vehicle speed. For non-linear distance in the vehicle platoon, di1,i is a non-linear function of the vehicle speed.
The expected distance between two adjacent vehicles is a nonlinear function of vehicle speed. Finally, the local controller at the node uses its neighbor information to control the node to achieve the desired vehicle platoon objective.
Adaptive Consensus Control
- Problem Statement
- Consensus Control Design
- Stability Analysis
- Simulation Results
The control objective of this summary is to construct an adaptive consensus control law 𝑢 such that all followers can track that of the leader without violating the output constraints. By providing the Lyapunov barrier candidate bound in closed-loop multi-agent systems, we can guarantee that production constraints are not exceeded. The first term is to minimize the error between the optimal signal 𝑣 and the virtual control law 𝑣.
The efficiency of the consensus control of the second-order nonlinear systems consisting of (5.1) and (5.2) is summarized by the following theorem. From the above analysis, we can conclude that the output signals remain in a compact set whose boundary is related to the design parameter 𝜆 and the communication graph 𝒢. Therefore, the proposed adaptive fuzzy consensus control method can achieve uniformly finite bounded control, the tracking error converges to a bounded compact set, and the output constraints are not violated. As for the quadratic Lyapunov function, the consensus control can be realized without violating the output constraints if the initial condition satisfies ||𝑒 0.
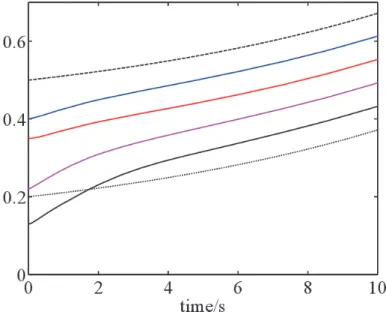
The simulation results of the proposed method of adaptive fuzzy consensus control through neurodynamic optimization (Scheme I) are shown in Figures 5.2-5.4. We can see that the positions of all the followers can be synchronized with the positions of the leader. From the above simulation, we can conclude that the proposed adaptive fuzzy consensus control approach can realize consensus control of output-constrained second-order nonlinear systems with unknown dynamics.
Adaptive Containment Control
- Problem Statement
- Distributed State Feedback Containment Control
- State Feedback Containment Controller Design
- Stability Analysis
- Distributed Output Feedback Containment Control
- Output Feedback Containment Controller Design
- Stability Analysis
- Simulation Results
The defuzzifier maps the fuzzy set in R to a crisp point in R. Since the strategy of single-element defuzzification, center-average defuzzification, and product inference is used, the output of the fuzzy system can be formulated as . 6.3), where 𝜃 is the point at which the fuzzy membership function 𝜇 𝜃 reaches its maximum value. Then all the signals in the closed-loop ti-agent systems are UUB and the hold-down control errors are satisfied. The containment control designed in Section 6.2 is based on the assumption that the states of the systems are measured directly.
Then all signals in closed-loop systems are UUB and the hold-down control errors are satisfied. In [97], a consensus scheme for nonlinear multi-agent systems (6.1) was developed, which means that the proposed method can ensure that all follower states are synchronized with the state of a single leader. In this paper, a containment control approach is designed to ensure that all follower states remain within a dynamic convex hull formed by multiple leaders.
A simulation example is given to show the effectiveness of the proposed distributed generation feedback inhibition controllers. It can be observed that the proposed braking scheme can realize that the states of the followers converge on the convex hull formed by those of the leaders, i.e. it can be observed that the designed retention controllers guarantee stability and good retention performance of the closed block. looped multi-agent systems with unknown dynamics.
Conclusion and Future Works
Conclusion
Yang Yu and Kang-Hyun Jo, "Output feedback fault-tolerant control for a class of discrete-time fuzzy bilinear systems." International Journal of Control, Automation and Systems, Vol.14, No.2, pp Yang Yu, Wei Wang and Kang-Hyun Jo, "Adaptive Consensus Control of Output-Constrained Second-order Nonlinear Systems via Neurodynamic Optimization." Neurocomputing, volume 295, pp. IF. Chen, “Distributed consensus of second-order multiagent systems with heterogeneous unknown inertia and control gains under a directed graph,” IEEE Transactions on Automatic Control , vol.
Boulkroune, "Adaptive fuzzy feedforward control for input-delay tight-feedback systems," IEEE Transactions on Fuzzy Systems, vol. Zhang, “Neural network-based adaptive leader tracking control for multiagent systems with uncertainty,” IEEE Transactions on Neural Networks and Learning Systems, vol. Jovanovic, “Optimal control of vehicle formations with nearest neighbor interactions,” IEEE Transactions on Automatic Control, vol.
Jovanovic, "Algorithms for leader selection in stochastically forced consensus networks," IEEE Transactions on Automatic Control, vol. Li, “Fuzzy adaptive decentralized output feedback control for large-scale nonlinear systems with dynamic uncertainties,” IEEE Transactions on Fuzzy Systems , vol. Li, “Adaptive fuzzy output feedback tracking feedback control of tight-feedback nonlinear systems with unknown dead zones,” IEEE Transactions on Fuzzy Systems , vol.