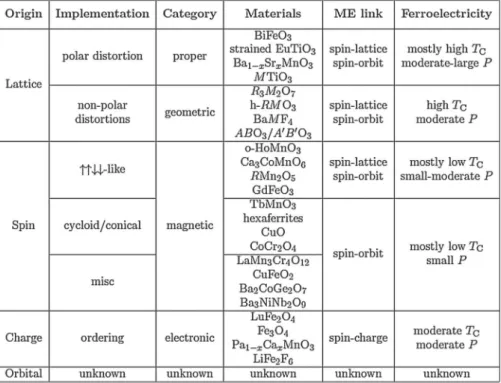
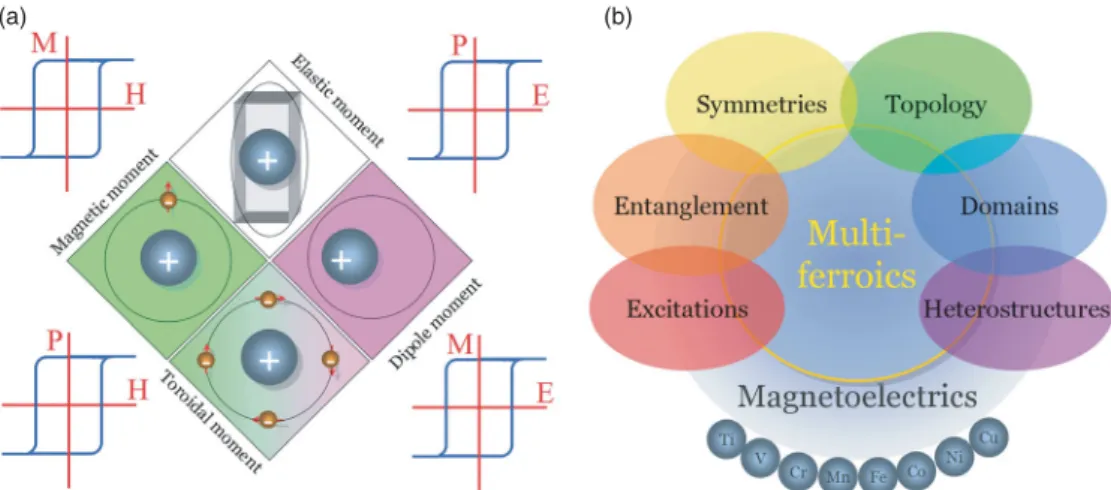
Schematic landscape of multiferric and magnetoelectric materials. a) The version proposed by Eerenstein et al. 16], where only ferromagnetic + ferroelectric materials are called multiferroics. The bulk crystal structure of BiFeO3 at room temperature is a rhombohedral perovskite in which the oxygen octahedra rotate alternately along the pseudocubic [111] axis (i.e., a−a−a− type distortion in the Glazer notation [17]), as shown in Figure 3(d ). The red shade indicates the pseudocubic (111) plane. f) Geometric (orthogonal) relationship between three vectors: polarization (P) along the pseudo-cubic [111]-axis, antiferromagnetic order parameter (L) and oblique magnetization (M). g).
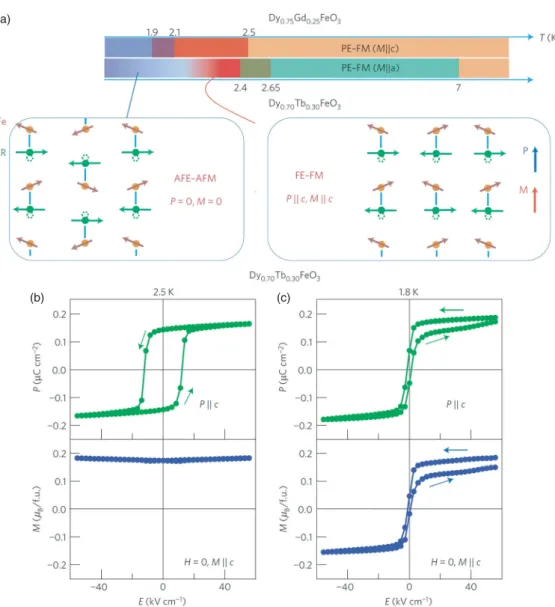
Khomskii emphasized the physical importance of type II multiferroics and hailed the discovery of type II multiferroics as "the greatest excitement today."
Phenomenological approach: symmetry and coupling
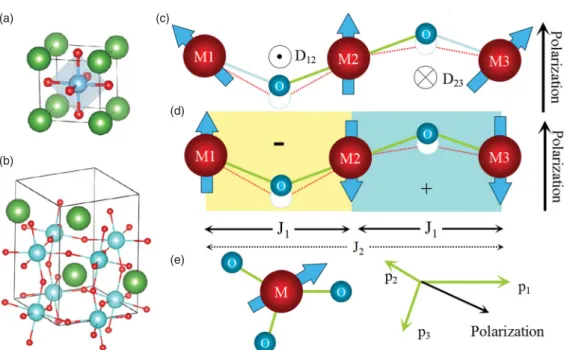
In contrast, the magnetic moment M, or namely spinS, breaks the time-reversal symmetry, but retains the space-inversion symmetry, because a magnetic moment can be expressed as ∼(dQr/dt)×r(t: time), by analogy to a current loop. For example, α can be written as ∂J/∂x, where J is the exchange interaction between the nearest neighbor sites and x is the bond length. For example, a term for magnetoelectric coupling yielding a time-dependent ferroelectric polarization can be written as.
The helicity (chirality) and parity related magnetoelectric coupling mechanisms can be self-consistently covered by this unified model.

Magnetoelectric coupling in single phases: from physics to materials
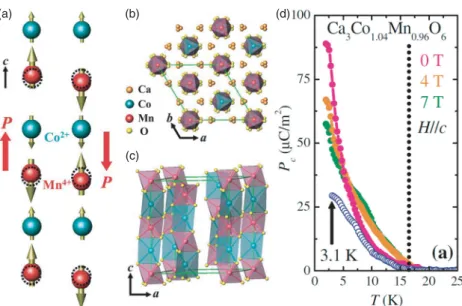
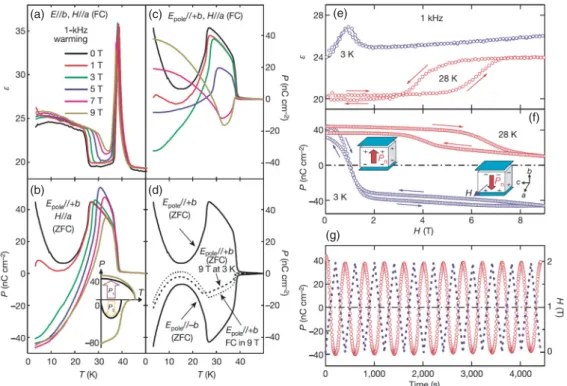
The original ionic positions are shown as dashed circles, while the coherent displacements lead to a P polarization. b) and (c) Projected views of the crystal structure. d) Pyroelectric polarization along the thec axis of Ca3Co1.04Mn0.96O6, which is suppressed by a magnetic field along the thec axis. Inset: a ferroelectric loop measured at 35 K. d) Capacitance-temperature cycle measured along the axis direction. e) and (f) Pyroelectric polarizations measured in different electric pole fields (Ep). Inset: pyroelectric polarization at 4 K as a function of polishing field. f) Pyro-electric polarizations under different magnetic fields.
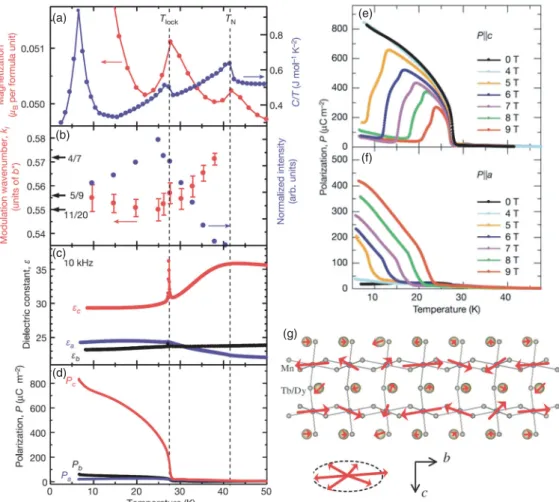
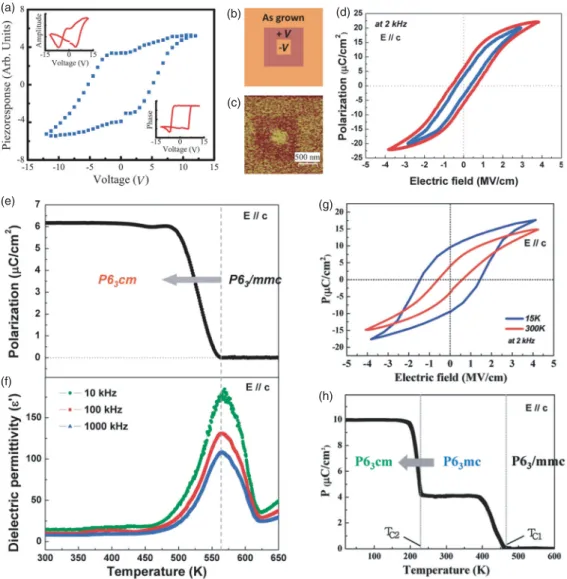
Pyroelectric polarization showing the Curie temperature at 563 K. f) Dielectric permittivity data measured at different frequencies show the corresponding peaks. d)–(f). Polarization reversal induced by a moving magnetic field: (e) dielectric constant as a function of magnetic field at 3 K and 28 K; (f) total polarization as a function of magnetic field at 3 K and 28 K, calculated from the magnetoelectric current measured after cooling to zero magnetic field, inset cartoon: polarization rotation;. g) polarization reversal sequence at 3 K, induced by linear cycles of the variable magnetic field from 0 to 2 T, clearly showing the highly reproducible polarization transition by the magnetic field. The B sites are occupied by Mn¯ 3.25+ cations at high temperature, but replaced by the 3 Mn3+ + Mn4+ lattice with charge below 250 K. c) and (d) Noncollinear magnetic structure between 48 K and 90 K in rhombohedral (c) abandon (d) planes. f) Pyroelectric polarizations measured along different axes. g).
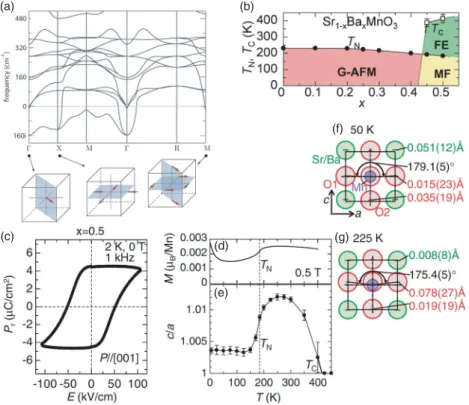
CuO among various cuprates has a moderateJ. The original J–f plot for cuprates was presented in Ref. The measured phase diagram of RMnO3 compared to the predicted diagram in (d). f) The zero-temperature polarization as a function of Jb (in relation to decreasing R3+ size). PS: contribution of the symmetric exchange striction (S·S); PAS: contribution of the asymmetric DM interaction (S×S) .P( Exp.): experimental data on Eu1−xYxMnO3and Y1−yLuyMnO3, in good agreement with PS+PAS. a)–(d). Figure reprinted with permission from Mochizuki et al. g) The ground state phase diagram of RMnO3 as a function of the nearest-neighbor superexchanger (JAF) and the next-nearest-neighbor superexchanger (J2) along the b axis, calculated using the two-orbital double-exchange model .
As expected, the electromagnon is negligible in the thex=0.2 case. d) Energies depending on phonon, magnon and electromagnon substitution in Eu1−xYxMnO3. e). A scheme of two electromagnon modes in the cycloidal spin state of the ab-eu0.55Y0.45MnO3.q plane: magnon wavenumbers. a) Coupling electromagnon: AC electric field along the thec axis causes a rotational vibration of the plane of spiral rotation about the theb axis. The peak at 2.7 meV in (c) is due to the conventional antiferromagnetic resonance driven by the component Hω|| of light (not discussed here). e) Experimental setup for measuring directional dichroism.
In the +kω case (Eω, Hω) can drive the vibration of both Pan and M (upper panel), while in the −kω case, light suppresses the vibrations of both P and M (lower panel). f) The time domain waveform of the transmitted terahertz pulses in different configurations (black and blue) and their difference (red). G).
Magnetoelectric coupling in thin films and heterostructures: from science to devices In parallel to extensive research on synthesizing single-phase multiferroics and exploring rele-
Inset, isothermal magnetization hysteresis loops at 1.8 and 3.8 K. f) Temperature-dependent second harmonic generation (SHG) intensity, showing that only EuTiO3 in DyScO3 (red) is polar below 250 K and others are non-polar. g). In addition to manganites, the charge-order transition (i.e. Verwey transition) of Fe3O4 can be tuned by the piezostrain of the PMN-PT substrate [325]. An electric field-induced shift of the ferromagnetic resonance in Fe3O4/Pb(Zr1−xTix)O3 and Fe3O4/PMN-PT heterostructures was also reported, bringing about a giant tuning of microwave magnetism [326].
A comparison of the two phase diagrams (inset) clearly illustrates the magnetic switching (different colors) by ferroelectric polarization: an FM/AF switchable white area. The resistance (g) and the magnetic moment (h) as a function of the magnetic field. i) The current-voltage characteristics of the node measured at 4 K after the upward and downward electrical poleing of the ferroelectric BaTiO3 barrier. A control of the exchange bias using magnetoelectric coupling would provide a new path to control magnetism.
The first demonstration of electric field-controlled exchange bias was reported in [Co/Pt]/Cr2O3(111) heterostructures [400,401]. A close coupling of the exchange bias with distinct ferroelectric domain walls in BiFeO3 was suggested [20]. More exciting is an observation of two distinct exchange bias states which can be reversibly operated by switching the ferroelectric polarization of BiFeO3, as shown in Figure 35(b).
Figure reprinted with permission from Rondinelli et al. f) Calculated polarization (P) as a function of the number of perovskite unit cells (N) in (LaFeO3)N/(RFeO3)N. Along the stacking direction, the B site ions form the pattern B−B−B−B, analogous to the antiferromagnetic order of type ↑↑↓↓. i) Case with positive polarization; (j) the case with a negative polarization. k) Schematic Y–O-icosahedron (left), Fe–O-octahedron (middle) and Ti–O-octahedron (right) in the (YFeO3)2/(YTiO3) 2 superlattice. l) and (m) The point-charge model evaluated the individual contributions to the total polarization, taking into account the different Ueff values in the density functional calculations, where the Fe2+–Ti4+ couple is adopted. l) Insulating box; (m) the metallic case, where the total polarization can be surprisingly increased since the proper (negative) ferroelectric distortions of the Ti-O-octahedrons are suppressed by the metal, while the improper ferroelectric distortions from the Y-O-icosahedron persist strongly independent of metallicity. h)–(m) Figure reprinted with permission from Zhang et al.
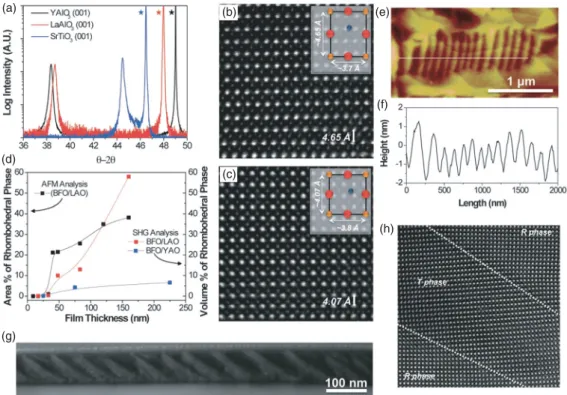
Magnetoelectric topology: monopole and vortex
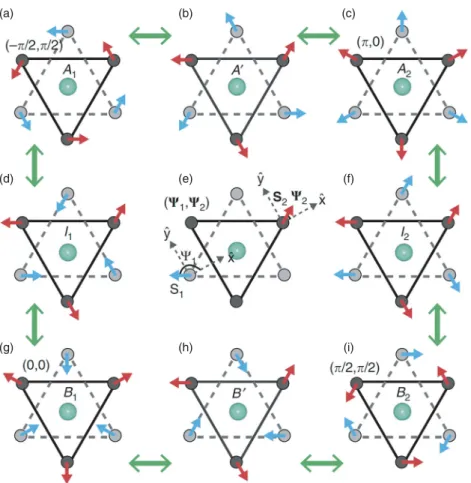
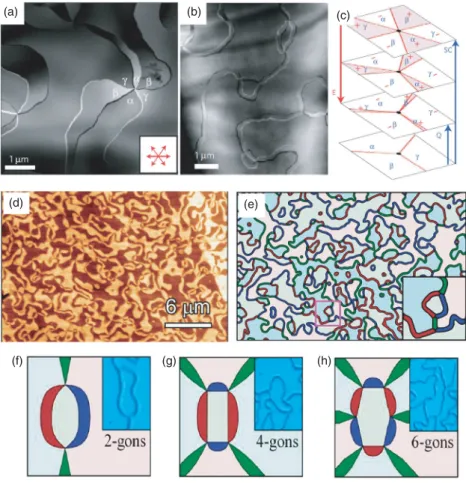
Ferroelectric domain vortex in hexagonal RMnO 3
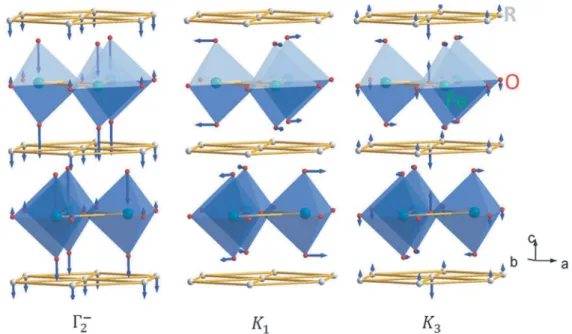
The ferroelectric polarization, which is also a result of trimerization, comes from the ↑ − ↑ − ↓ shifts of the Rspin trimers and is aligned along the c-axis (+ or . Conversely, if the sample is above the ferroelectric Curie temperature is grown, the vortex patterns due to the structural trimerization appear above the ferroelectric Curie temperature. Theoretically, the complex topological ferroelectric domain structures can be understood in the framework of the Landau theory using density functional calculations [475].
The three domains of negative ferroelectric polarizations seriously shrink into narrow ribbons, but cannot be completely melted due to the robustness of the domain walls, proving that the vortex core is topologically shielded. Contour plot of free energy for uniformly trimerized states as a function of trimerization (amplitude Q and phase). Because of the Mexican hat-shaped potential well, any domain wall beyond ±π/3 has a much higher energy and is therefore unstable against spontaneous decomposition into multidomain walls.
Of course, these domain walls can terminate at the surface or an antivortex, resulting in the vortex-antivortex pairs connected by domain wall strands [123] . In addition, the annihilation between a vortex and an anti-vortex is possible [474], analogous to the annihilation between an elementary particle/antiparticle. A cartoon showing the effective magnetoelectric coupling through structural trimerization. f) Cartoons showing a variation of the buckling of MnO5polyhedra (trimer modeQK3) induced by electric fields via polarization component Pz, leading to a variation of the tilted momentMzof Mn spin.
Copyright c(2014). domains, but defined by the magnetoelectric coefficient) can be visualized, as shown in ErMnO3, where the magnetoelectric domains are clamped to the structural-antiphase domains mentioned above (see figure 44 for more details) [476]. Nevertheless, an electric field will shift the Dirac surface state to a momentum direction by a small amount, resulting in a change of the Fermi surface.
Summary and perspective
This coupling is stuck by the spin-orbit coupling and no net magnetic moment is available by integrating the entire surface state. However, no material in the two families was found to be multiferroic until recently when Dong et al. The crystal structure of BaFe2Se3 is shown in Figure 46(a)–(c), which has two iron ladders (marked as A and B) in each unit.
As shown in Figure 46(b), the Se(5) and Se(7) heights no longer need to be anti-symmetric with respect to the Fe scale plane. As confirmed by density functional calculations, both Block-EX and Block-MF are multiferroic. The PMF is large and along the a axis (~2–3µC/cm2). The net polarization of Block-EX is along the thec axis and its magnitude is about 0.19µC/cm2.
Taking advantage of density functional calculations which are becoming powerful, new materials to be synthesized with promising properties can be "designed" by computers. Near-room-temperature ferromagnetism due to strong Ni–Mn exchanges was predicted, and a ferroelectric hybrid mispolarization induced by the geometrical mechanism as previously reviewed is believed. The d0 state is likely to be ferroelectric while the thed1 state may be ferromagnetic or antiferromagnetic.
However, the magnetic origin of ferroelectricity in these multiferroics appears to be outside of currently known mechanisms. While the multiferroicity of these materials can be covered with the phenomenological theoretical framework, the proper microscopic mechanisms should remain accessible. Moreover, our understanding of the domain wall vortex in hexagonal RMnO3 and magnetoelectricity at domain walls is far from complete.
Of course, one of the ultimate goals of multiferroic and magnetoelectricity research is the use of multiferroic materials.