The proposed 20 chapters have been created in response to the very high demand for Mechanics of Materials courses. The presented short course is intended as a small supplement to the imposing classic books on the mechanics of materials.
1 BASIC INFORMATION ON MECHANICS
- Mechanics is the science on the equilibrium of mechanical motion of material bodies as a change over time in the space of the mutual position of
- The material body (material substance, physical substance, substance) is defined as a collection of discrete formations (atoms, molecules, and more complex
- The material point is the body having a mass and size of which is neglected in comparison with the distance to which it is displaced
- The rigid body is the body that does not change its dimensions with the given shape (does not deform)
- A lever is called a long rod, which is based on a distance from one end to the fixed support and to which vertically forces are applied on both ends
- The statics of fluid was studied even in ancient times. The mentioned above Archimedes law “the main vector of the pressure of the fluid on the surface of
- The vortex is called the form of motion of the fluid, which is described by an antisymmetric part of the velocity gradient; accordingly, the motion
- The phenomenological law is thought in mechanics as the well substantiated empirical law with the restricted and also well substantiated area of
- In essence, every theory is phenomenological, since otherwise we would have reached an absolute penetration into the nature of things, which is impossible
- The term empirical comes from the Greek word for experience - ἐμπειρία
- The empirical evidence is an information received by means of the senses, particularly by observation and experimentation, in the form of recorded data,
- In science, the de Groot’s empirical closed cycle is well-known: 1.Observation
Newton's Law of Universal Gravitation "The bodies are mutually attracted by a force proportional to their masses and inversely proportional to the square of the distance between them" is the basis of celestial mechanics. The above-mentioned Archimedes' law "the main vector of the pressure of the liquid on the surface of above Archimedes' law" the main vector of the pressure of the liquid on the surface of.
2 BASIC INFORMATION ON
MECHANICS OF MATERIALS
THEORY OF ELASTICITY. SHORT DESCRIPTION OF LINEAR
THEORY OF ELASTICITY
- SOLID MECHANICS (MECHANICS OF MATERIALS) is the part of mechanics that studies the deformation of materials
- ELASTICITY: the body instantaneously takes on the initial configuration after eliminating the causes of deformation (deformations are reversible)
- The creep of deformations consists in increasing the deformations under conditions of stress constancy
- The relaxation of stresses consists of decreasing stresses under con- ditions of deformation constancy
- VISCOPLASTICITY: the phenomenon of creep is presented and at the same time the body is deformed plastic
- DIFFUSIONAL ELASTICITY: diffusion is the cause of elastic deformation and vice versa
- ELECTROELASTICITY: the electric field is the cause of deformation and vice versa
- MAGNETOELASTICITY: the magnetic field is the cause of deformation and vice versa
- There are different criteria for distinguishing the shown above parts of the theory of elasticity. One of the frequently used criteria is that Part I uses the
- An analysis of balance equations (conservation laws) has proceeded from the well-known statement: ”the great laws of classic physics can be considered as
- The material is called the isotropic one, when its mechanical properties are identical in any direction
- Three conditions of equality of values of the internal stresses on the body surface V ik k Sn and the external surface force
- Different kinds of mixed conditions can be formed by the procedure, when at the point of surface are given one or two components from Type 1 and
- Just this approach was implemented by Kolmogorov in the axiomatization of probability theory and further by Noll and Truesdell in the axiomatization of
- The ergodicity theorem is physically meaningless if the characteristic time of the system is commensurate (longer) with the time it takes to determine
Let's start from the brief information on the above four parts with the Part II – the linear theory of elasticity. But then the equations (2.9) introduced six new unknown functions – the components of the strain tensor.
3 SOME ADDITIONAL
FUNDAMENTAL FACTS FROM THE LINEAR THEORY OF ELASTICITY
Write the body's internal energy (work of deformation) for the deformation state (3.8). It is believed that the proof is complete and the solution of the fundamental problem of the linear theory of elasticity is unique.
Three-dimensional (spatial) problems
Thus, the initial assumption that two solutions of identical equations of equilibrium and boundary conditions can be different becomes false.
Two-dimensional problems (including the plane problems)
One-dimensional problems
In the case where the external force FG is absent, the equations (3.19) have the solutions in the form of harmonic functions and the representation (3.18) has become very fruitful. In the case of absence of the external force, the function Mx x x1, ,2 3 is a harmonic one, and this representation gives the very simple formula.
In the proof of relations (3.25)-(3.29), the starting point is using Helmholtz’s representation
This implies a certain simplification of the equilibrium equations (3.12) and needs its representation through stresses and in cylindrical coordinates ^r, ,M z`. Nowadays, any problem on the statics of a three-dimensional linear elastic body of complex shape can be analyzed and solved with a certain level of accuracy.
The plane displacement condition arises in the analysis of deformation of the long in direction. The plane stress condition arises in the analysis of the deformation of the plate with small thickness loaded by the forces in the plate plane.
The body is in the plane stress state, if
Now some words about the tools used in the analysis of the plane problems in the linear elasticity theory. In the case of the singly connected field, the function F can be represented by two holomorphic (regular) functions, which is expressed by Goursat's formula.
The Levi’s theorem is very useful in the analysis of the multi-connected areas: If the resultant vector of forces applied to each contour separately is zero, then
It shows the relationship between the maximum and the voltage value at a given point. The progress in solving planar problems of linear elasticity theory is impressive from another point of view.
The conformal mapping of the certain simple-connected area of the plane
Let's stop in one direction - the development of new methods to solve the problem. The substitution of the last expression for dilation in the first equation (3.66) gives relations 3 2 2 xx 3 2 xx.
The universal deformations will be also discussed in the following chapters
A specimen has the shape of a cube on which the uniform surface load (hydrostatic compression) is applied to the sides. This type of universal deformation is defined by the following components of displacement gradients. 3.69) The Cauchy-Green strain tensor is as follows. 3.70) and the algebraic invariants are written in the form
Usually, the term “rod” refers to bodies of elongated shape, which resist only the forces of tension-compression and torsion
Usually, the term “beam” refers to bodies of elongated shape, which resist only the forces of bending
The next after rods and beams objects of analysis of the linear theory of elasticity are PLATES and SHEETS. Most of the textbooks on the linear theory of elasticity do not include the theories of plates and shells.
The plate is defined as the body of finite or infinite sizes bounded by two planes symmetric relative to some plane (middle plane; usually, the coordinate
IN FACT, SUMS AND THREES CAN BE ANALYZED IN THE LINEAR THEORY OF ELASTICITY AS SPATIAL BODIES WITHIN A THREE-DIMENSIONAL MIRROR FRAME. Note here once again that most textbooks on linear elasticity theory do not include plate and shell theories.
The SHELL is defined as the body of finite or infinite sizes bounded by two surfaces symmetric relative to some surface (middle surface of the shell) a
The deflections of the plate should be so small that the membrane forces in the middle plane can be neglected. A THICK PLATE is limited by smaller side to thickness ratio values of 10.
The stresses arising in the middle surface (it is characterized by coordinates
A segment of the normal to the midplane rests under load from the straight and normal to the midplane and does not change in length. The stresses perpendicular to the center surface are neglected compared to the stresses acting in the surface, such as parallel to the center surface.
The SHALLOW SHELL is defined as the shell that has a small clearance over the plane on which it rested
This allows the description of the change of the deformation state with time and the study of very important stationary and non-stationary mechanical phenomena, including vibrations and waves. The oscillation of an elastic body is understood as a change in the deformation parameters of the body (displacement, deformation, stress) that occur.
The vibrations of the elastic body are understood as a change of parameters of deformation of the body (displacement, strain, stress) which occur
As a result, the basic equations of statics (which is the elliptic type). 3.74) is transformed in the case of dynamics to the hyperbolic type. 3.75).
The vibrations of the elastic body are understood as the repeated limited motion relative to some mean value of the body state, which can be often
A motion is assumed as oscillatory, when it takes place in the neighbourhood of some fixed state, is restricted in its variation from this state, and
The theory of oscillations of linearly elastic bodies is a well-developed and structured part of the linear theory of elasticity. It is also part of the general theory of vibrations, which currently includes practically the entire spectrum of science from physics to politics.
The body, in which the wave propagates, is dispersive and the wave themselves is dispersive, if the wave is mathematically represented in the form of
The body in which the wave propagates is dispersive and the wave itself is dispersive if the wave is mathematically represented in the form of
The criteria of hyperbolic and dispersive waves are not mutually exclusive;
Solitary waves or pulses – the sufficiently short in time and irregular locally given in a body disturbances
Periodic (most often, harmonic) waves, which are characterized by the disturbances in all the body
Wave pockets – the regular locally given in a body disturbances
Trains of waves – the harmonic wave pockets
Finite element (FEM) and boundary element (BEM) methods should be related to this group. Two basic variational methods are used here - Lagrange's principle based on displacement variations and Castigliano's principle based on
Two basic variational methods are used here – the Lagrange’s principle based on variations of displacements and the Castigliano’s principle based on
Eslami, MR, Hetnarski, RB, Ignaczak, J, Noda, N, Sumi, N & Tanigawa, Y 2013, Theory of elasticity and thermal stress. Starovoitov, E & Naghiyev, FBO 2012, Foundations of the theory of elasticity, plasticity and viscoelasticity, Apple Academic Press, Palo Alto.
4 SHORT DESCRIPTION OF NONLINEAR THEORY OF
- The motion is the mapping of a set
- The configuration of a body at time
- The configuration of a body at any arbitrarily chosen initial moment is called THE REFERENCE CONFIGURATION
- The description of body motion by the reference configuration is called THE REFERENCE DESCRIPTION
- THE DEFORMATION OF BODY is meant as a change of the shape or dimensions of the body
- THE GRADIENT OF DEFORMATION is defined as the vector
- The expression (3.3) is called THE FUNDAMENTAL QUADRATIC FORM
- THE FUNDAMENTAL METRIC TENSOR is defined as the tensor with
- The contravariant and mixed components are defined analogously. When being passed from the curvilinear coordinate system to the Cartesian one, then all
- It is appropriate to mention here that the strains characterize the change of the body form or dimensions in whole and the relative displacements of the
- The relations (4.6),(4.7) are quadratically nonlinear relative to gradients of displacements
- It is accepted that the displacement vector (4.2) and strain tensor (4.8) or other pair – the displacement vector (4.2) and strain tensor (4.9) – describe
- Both tensors are nonlinear, symmetric, positively defined and their main values are positive
- Three first algebraic invariants of these tensors are as follows
- The formulas (4.10) use the standard operators tr and det, which are also shown in representations by components of the strain tensor
- Three only of a countable set of all the invariants are independent;
- The Lagrange-Cauchy stress tensor
- In the nonlinear theory of elasticity, two different operations of the differentiation of tensors are used. The first characterizes the rate of changing the
- Recall once again that the reversibility of deformations after removing the causes of these deformations is assumed as the basic property of elastic deformations
- For different ways of the deformation description, it is convenient to use different strain tensors (and respectively, different strain rate tensors) and
- THE GENERALLY ELASTIC MATERIAL is called the material which can be in the natural (free of stresses) state and in a neighborhood of this
- A presence in definition (4.16) the asymmetric rotations strain velocity tensor with components W kn v [ , ]k n v [ , ]k n
- The hypoelastic material is the material the constitutive equations of which are given in the form
- THE HYPERELASTIC MATERIAL is the elastic material for which the specific internal energy (the potential)
- The representation of potential depends on which kind of strain tensor is used. For example,
- M can be called the model of the real object O , if it is constructed for the imitation of the behavior of O by characteristics Ch (or some part of them)
- Because the model is constructed relative to the set of characteristics and has the goal to study these characteristics, it is always simpler than the real
Just for this purpose, the above configurations – the reference configuration (at the initial moment) and the actual (at the current moment) one – are fixed. But further in the construction of the theory of deformation, the new concept – the gradient of displacement – is used, which is only the linear approximation of the change of displacement.
5 SHORT DESCRIPTION OF NONLINEAR THEORY OF
- The experiments play a crucial role in judgment on the area of applicability of the mechanical models. The theory of elasticity worked out the special tool for
- It is in place to note that the simpler variant of representing the potential through invariants (the potential for a linear elastic body with elastic Lame modulus
- Elastic materials are divided on compressible and incompressible by the criterion of changing the volume of the elastic body. The compressible material
- The Wikipedia notes that, in anatomy, the soft tissue includes the tissues that connect,support, or surround other structures and organs of the body, not being hard
- The Signorini potential (5.5) corresponds to the particular case of function
- When the experimental data are obtained for the wide spectrum of strains (from very small to the large) and some nonlinear model describes well the interval
- Let us recall here the formulas for the used above invariants
- The Mooney-Rivlin potential (4.13) corresponds to the case
- The terms “second order” and “third order” corresponds to presence in (5.35) the Lame elastic constants in the second order summands and the Murnaghan
John proposed to take into account in equation (5.4) the invariants of the nonlinear Green tensor. He used the nonlinear elastic deformation model which is now called the "Mooney-Rivlin model".
6 SHORT DESCRIPTION
OF LINEARIZED THEORY OF ELASTICITY
- The motion is the mapping of a set
- The configuration of a body at time
- The configuration of a body at any arbitrarily chosen initial moment
- The theory of elasticity uses a series of characteristics of the process of deformation of body (state of body)
- It should be born in mind that in this case the quantities y and x are the tensors of the 2 nd rank and the function F is the function of many variables
- The formula (6.18) can be reduced to the formula (6.15) for the linear theory of elasticity if only the reference (non-perturbed) state is natural (non-
- When the linearized constitutive equations and expressions for the strain tensor are substituted into the basic equations (5.32), then these last remain the
- st variant of the theory of small initial (non-perturbed) strains
- The smallness of the components of the Cauchy-Green strain tensor
- nd variant of the theory of small initial (non-perturbed) strains
- rd variant of the theory of small initial (non-perturbed) strains
The partial case was often studied in linearized elasticity theory - the case where the initial (base) state is uniform. Together with the constitutive equations, they form the basic system of equations of linearized elasticity theory.
7 SHORT DESCRIPTION OF STRENGTH OF MATERIALS
The strength of materials
The linear theory of elasticity
The linearized theory of elasticity
The nonlinear theory of elasticity
Strength is the ability of the material to perceive the external load without failure
Stiffness is the ability of the material to keep its geometric parameters within acceptable limits under external actions
Reliability is the ability of the structure or the structural members to function without failure. Reliability includes some restriction – it is considered
Stability is the ability of the material to maintain its shape and position in external influences
The strength of structures or structural parts is an important part of the strength of materials. THE STRENGTH OF STRUCTURES OR STRUCTURAL MEMBERS is determined by FAILURE THEORY - the science of predicting the conditions under which materials fail from external loads.
Theory of maximum normal stress. According to this theory, a failure occurs if the maximum normal stress
The problem is also to ensure the correct interpretation of the resulting information about future displacements, stresses and strains when evaluating the work and practical suitability of the structure or structural part. The theories of failure of structures or structural members can be divided into classical and modern.
This theory and the next theory of maximum strains deal with the brittle materials. The rest theories deal with ductile materials
Therefore, strength of materials, by its practical orientation, pursues goals that are broader than the theory of elasticity. The most important fact in the failure criterion is the surface of failure, expressed through stresses or strains.
Theory of maximum strains. According to this theory, a failure occurs if the maximum strains in some part of the structure exceeds the strains of the material as determined from
For a "damaged" condition, it is difficult to give an accurate physical definition, a concept that should be considered a working definition used in the engineering community. According to this theory, failure occurs if the maximum shear stress in some part of the structure exceeds the shear stress of the material as determined from the uniaxial stress-compression test.
Theory of maximum distortion energy. According to this theory, a failure occurs if the distortion energy per unit volume in some part of structure equals or exceeds the distortion
According to this theory, failure occurs if the strain energy per unit volume in some part of the structure is equal to or greater than the strain.
The strains generate total elastic energy which can be divided into two parts: one part causes a change in volume, and the other part causes a change in
Theory of maximum strain energy. According to this theory, a failure occurs if the strain energy per unit volume in some part of structure equals or exceeds the strain energy per unit
The classic failure theories have significant limitations for their application and are used today very limited.
Drucker–Prager’s yield criterion is written as follows
This criterion was proposed for the soil which is undergone to the plastic deformation and now is used in the analysis of rock, concrete, polymers, foams,
Tsai-Wu’s failure criterion is written in the form
The Willam-Warnke yield criterion is proposed for the analysis of concrete and is first written in the form. This explains the special place of strength of materials in materials science.
The rod is an elongated body, the two dimensions of which (height and width) are small compared to the third size (length).In the same sense, the
The failure theories and criteria are thus the inherent part of the "strength of materials" science. Now return to the first definition of strength of materials and describe the term.
Usually, the term “rod” refers to bodies of elongated shape, which resist only the forces of tension-compression and torsion
The Willam-Warnke yield criterion can be considered as a combination of the Mohr-Coulomb and Drucker-Prager failure criteria. In most cases, the structural elements are thought of as BARS, BEAMS, COLUMNS, PLATES, SHELLS and the structures that consist of the bars, beams, columns, plates and shells.
Often, the rod working on compression and placed vertically is called
This criterion is used in the analysis of concrete and other cohesive friction materials such as stone, soil and ceramics. The rod is an elongated body whose two dimensions (height and width) are small compared to the third dimension (length). In the same sense, it is.
Usually, the term “beam” refers to bodies of elongated shape, which resist only the forces of bending
The plate is defined as the body of finite or infinite sizes bounded by two planes symmetric relative to some plane (middle plane; usually, the coordinate
A shell is defined as a body of finite or infinite size bounded by two symmetrical surfaces with respect to some surface (the middle surface of the shell) a.
The shell is defined as the body of finite or infinite sizes bounded by two surfaces symmetric relative to some surface (middle surface of the shell) a
Because the waves are taken into account, the additional assumption of elementary theory must be made: the wavelength must be essentially the.
Because the waves are considered, then the additional assumption of elementary theory should be done: the wavelength has to exceed essentially the
In elementary theory, as the longitudinal wave propagates, it is assumed that the motion of particles in each cross-section is the same.
It is assumed in the elementary theory that, while the longitudinal wave being propagated, the motion of particles is the same in each cross-section
It is worthy to say that the exact theory of the torsional wave is essentially more complicated
But it has the solution in the form of the harmonic wave, which is called the bending wave. The exact approach to study the waves in the rod has the old history.
The limiting cases are considered relative to the ratio of the wavelength to the radius of cylinder
Limiting cases are discussed in terms of the relationship between the wavelength and the cylinder radius. This value of the phase velocity corresponds to the basic theory with Rayleigh refinement.
This value of the phase velocity corresponds to the elementary theory with the Rayleigh’s improvement
If the first root is denoted by Ktors(1), then the corresponding phase velocity is determined by the formula. For small wavelengths, the phase velocity is close to the transverse wave velocity.
It is assumed that a motion of the element of the rod occurs in the way that each cross-section rotates as a single item around the axis of the rod. To take
The shown example of the elementary and exact theory of propagation of waves in the circular rod (cylinder) demonstrates a deep difference between approximations of the strength of materials (elementary theory) and the linear theory of elasticity (exact theory). Should they be considered as the structural members or as the separate object of the strength of materials.
8 FOCUS ON COMPOSITE
MATERIALS. DIFFERENT MODELS OF ELASTIC DEFORMATION
The homogeneous materials are understood as materials with the internal structure of atomic-molecular character (with the characteristic size of the
The heterogeneous materials are understood as materials with internal structure essentially more than molecular-kinetic sizes (sizes of molecules, crystal
The intermediate place between the homogeneous and heterogeneous objects is occupied by the colloid mixtures and micellar solutions. But they can
The composite materials (composites) are conventionally defined as consisting of a few components (phases) with differing physical properties. As a
The rigid component is considered the reinforcing or reinforcing component and is usually referred to as the filler, while the soft component is conditionally referred to as the matrix (the binder). Thus, the most famous and widely used granular composite materials consist of the grain-reinforced matrix, the fibrous composites consist of the fiber-reinforced matrix, the layered composites mainly consist of two alternating layers, and the stiffer layer is believed to be the to be matrix.
In the case when some areas of free space (voids) between components exist, these areas are treated as pores representing one more component, and such
As a rule, the internal structure of composite materials assumes the leaping (stepwise) change of properties of components (phases) at interfaces and the presence of the soft and rigid components. The internal structure of composite is shown here in the same way as it is done for engineering and construction materials (steel, iron, wood or plastic).
In most cases when the matter concerns the averaging properties, it is understood as working within the framework of the classical continuum model of
The macro-description of materials predominated in the mechanics of materials until the 20th century, when meso-description and micro-description were proposed and developed in the second half of the 20th century (the first was mainly due to the deep analysis of metals; (. the second due to the extensive fabrication and application of composite materials.) Virtually all models of the mechanics of materials are based on the introduction of a continuum.
The continualization principle is applied to the substance (material) that is meant as some discrete structure, whereas the homogenization principle is applied
The principle of homogenization is widely used in the mechanics of composite materials and, more abstractly, in the structural mechanics of materials when it seems expedient to use homogeneous material models. For a substance (material) that is thought of as some discrete structure, the principle of continuousization is used, while the principle of homogenization is used.
The parameter
Limitation of the number of inhomogeneities (molecules, formations of different scales – micro, nano) – the representative volume must contain a sufficiently large number of inhomogeneities (eg grains).
Usually, most of the authors are assuming that exceeding the first value over the second value on one or more orders gives grounds for the next modeling
There exist some additional restrictions that provide the averaging procedure. For example, the variability of mechanical fields in the body must be
In the classical theory of elasticity, the constitutive equations describe only the elastic deformation properties. In the linear theory of elasticity, energy is postulated as a quadratic function of stress.
The crystalline materials permit many types of symmetry. Ten of them are the most widespread
This brief explanation of the foundations of the theory of constitutive equation in the linear theory of elasticity seems to be sufficient for the following analysis. The characteristics of the internal structure are simply taken in this model - in the average elastic constants of a homogeneous anisotropic medium using the principle of homogenization.
For materials internal structure of which can not be changed significantly under manufacturing and obtain some essential changes in their properties, the
It seems useful to first show THE CLASSICAL MODEL which reduced an analysis to the theory of elasticity with average elastic constants. Therefore, the most well-known theoretical formulas for the evaluation of average elastic constants can be useful and meaningful.
It is considered that the constitutive equations and determination of physical constants for some set of composite materials are related to the fundamental
We can comment on this situation by saying that it is not necessary to evaluate the elastic constants for materials whose internal structure cannot be significantly changed in order to achieve some significant changes in their properties. Thus, this theory proposes formulas for estimating the elastic constants of heterogeneous materials (usually two-phase).
The formulas (8.8),(8.9) express the rule of mixture
L (longitudinal) is used to denote properties along this axis, T (transverse) index is used to denote properties in the plane. But in the case of using the isotropic material model these formulas are quite simple.
Let us cite the classical Broutman&Krock’s book “It should be understood, of course, that the mechanical behaviour of the components is not always known
Second, because of the difference between the mechanical properties of granules, fibers, foils, etc., and the properties inherent in standard samples of the same material. L MD are linear differential operators of the 2nd and 4th order respectively (the last operator introduces in the 3rd equation the concept of effective stiffness); displacements.
It turned out afterward that other structural models possess this property too. But the Bolotin model was the pioneer one
The averaged global displacements are then equated with the displacements at the center of the fiber in the initial discrete cell system. The density of the strain energy in the new continuum depends on the effective moduli, but includes additional constants depending on parameters of the microstructure and has a sense of effective stiffness.
Some disadvantage of models of effective stiffness (like to the most of structural models of composite materials is that they describe only the first, lowest,
Overall, continuum theories of different orders have been obtained as a function of the number of terms retained in the representations of the energy densities. Theories based on discrete models of lattices form the isolated direction in the microstructural analysis of composites.
One should remark that the authors of the non-continuum lattice models have participated in the construction of many other structural continuum models
The fact of asymptotic expansion is assumed here as the main one and, in this regard, such a model is related to models, which are based on asymptotic expansions. In general, such continuum approaches give better accuracy in describing dispersion curves than many other models.
It is widely assumed that the continuum theories of composite materials have some advantages over discrete ones. First of all, for the reason that they are
It is widely believed that the continuum theories for composite materials have some advantages over discrete ones. The classical model of elastic deformation is essentially simpler and is based only on the macro-strain tensor Hij 1 2 uj i, ui j,.
This was done in the context of micromorphism theory by Eringen, Maugin, and others and later continued for mixture theory. Where the subject of interest is wave propagation in granular powders so that the wavelengths are sufficiently close to the characteristic size of the microstructure.
Where the subject of interest is wave propagation in granular powders such that the wavelengths are sufficiently close to the characteristic size of the microstructure
Together they form only a basis for understanding the theory of composite materials that develops in the structural mechanics of materials. Expand the list of natural composite materials used in private life.
9 FOCUS ON COMPOSITE MATERIALS. STRUCTURAL
MODEL OF ELASTIC MIXTURES
The composite materials are the typical representative of the heterogeneous materials. The simplest case of the real composite materials is when they consist of
For denoting the real mixture and the mixture as the theoretical model the same term “mixture” is used
The construction of a mixture theory suitable for composite materials was initiated by Lempriere, Bedford, Stern publications in which the shear model of the interaction of forces between phases. In terms of the phenomenological model of the mixture, this means that the interaction of forces between the phases is directly proportional to the difference of the phase shifts.
Following traditions of mechanics of heterogeneous media, the parameter is named partial if it characterizes one phase only
In the case "separately" the theory used the physical constants of each phase, while in the case "as a whole" the phase constants are not used. The motion of each mixing phase will be described with respect to fixed orthogonal Cartesian coordinates.
It is considered that the constitutive equations and determination of physical constants for some set of composite materials are related to the fundamental
Let's start with the simplest formulas for the evaluation of physical constants, based on the simplest considerations and the deterministic concept. The constitutive equations are assumed in the form (9.9) taking into account the transverse isotropy of the mixture.
The above formulas for effective constants are very simple. But this simplicity is caused by the very simple theoretical schemes used and by strong
But this simplicity is caused by the very simple theoretical schemes used and by strong. More complicated and closed to the above stochastic approach was realized for granular compositions with an ellipsoidal shape of grains.
Some more complicated and closed to the described above stochastic approach was realized for granular composites with an ellipsoidal form of granules
In assuming
These formulas are obtained in the approach valid only for large time wave propagation
When lCDM is close (one or less orders) to the wavelength and this wave is a so-called short wave, then corresponding to this wavelength frequency can be treated as very large. Here and later the redundancy of the number of equations appears relative to constants since the fourth equation of (9.21) for different types of.
Here and later the redundancy of the number of equations relative to constants is seeming since the fourth equation from (9.21) for different types of
The latter depends only on the symmetry of the mechanical properties of the mixture and does not depend on the type of wave.
In the 2nd phase of a mixture, the 1st mode is similar to the wave (9.36), but with the same property that it additionally has a special amplitude coefficient that depends on properties of the mixture, frequency and wave numbers. Therefore, the wave propagation has been one of the most studied phenomena in the composite materials.
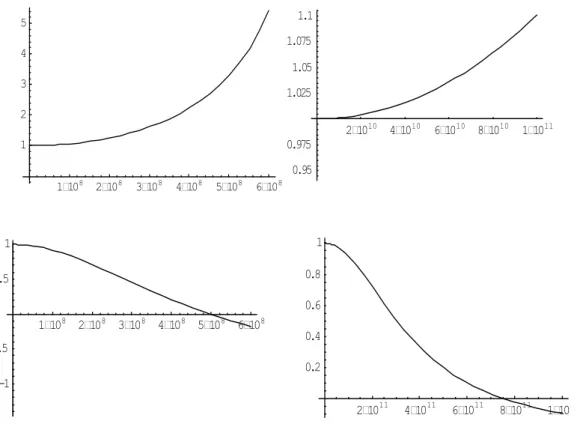
The geometrical dispersion in materials is called the dispersion which arises owing to the presence in materials both of the internal structure and the
The last issue we will discuss here is related to experiments with plane waves in materials. Geometric dispersion in materials is called dispersion that arises due to the presence in materials of both internal structure and.
The viscoelastic dispersion in composite materials is usually the effect of the viscoelastic properties of the matrix of composites
The prevailing view is that any observation must be concentrated on a number of selected phenomena and that the description or explanation of this observation is based on some theoretical scheme. In experiments with plane and volume waves, the dispersion of different nature - geometric, viscoelastic and constructive - seems too difficult to separate.
The constructional dispersion arises when waves interact with the boundary surfaces of the constructions
Why mixture theory is related to second-order structural theories. Find experiments that demonstrate the presence of two modes of plane elastic waves in composite materials.
10 FOCUS ON NEW MATERIALS NANOMECHANICS
OF MATERIALS
- The most part of facts presented in this chapter corresponds to the book Guz&Rushchitsky on nanomechanics which is shown in the Further reading
- The prefix nano- means one milliard part (nano in Greek means dwarf)
- The word “nanotechnology” was coined by Taniguchi in 1983 to describe the lower limit in ultra-precision engineering
- Because nanoparticles can be the basis both for nanomaterials and for nanopowders, then it is necessary to note that in mechanics the powders are considered
- Let us note that the atom level (distance between atom planes in the crystal lattice) has the order one or more angstrom (
- The Fig.10.5 shows two features of nanofilms: a thickness of nanofilm has always the nanosize and also the forming of film nanorods have the nanosize;
The most important tools in working with nanomaterials – the electron microscopes – were produced relatively recently. When the graphite sheets roll up to the ring and the ends meet, they form nanotubes – the molecules with a multitude of atoms.
