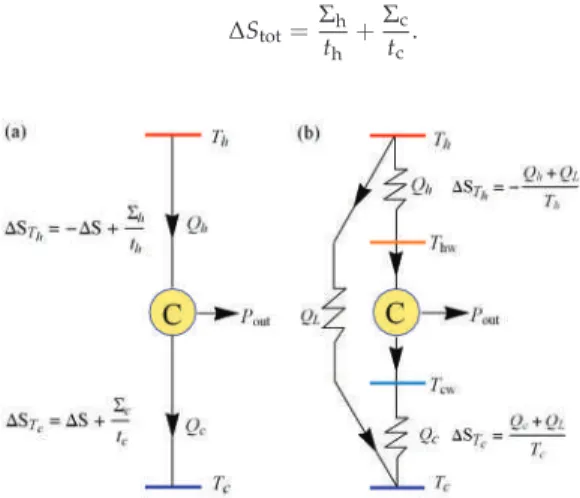
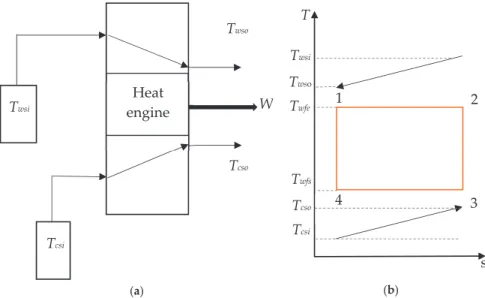
A detailed analysis for different heat transfer laws in the Carnot-like model in terms of maximum power efficiency given by the low-dissipation model is also presented. In irreversible Carnot-like HE, the entropy generation of the internal reversible loop is zero and the total entropy output is that generated in the external heat reservoirs (see Figure 1b).
Physical Space of the HE Variables
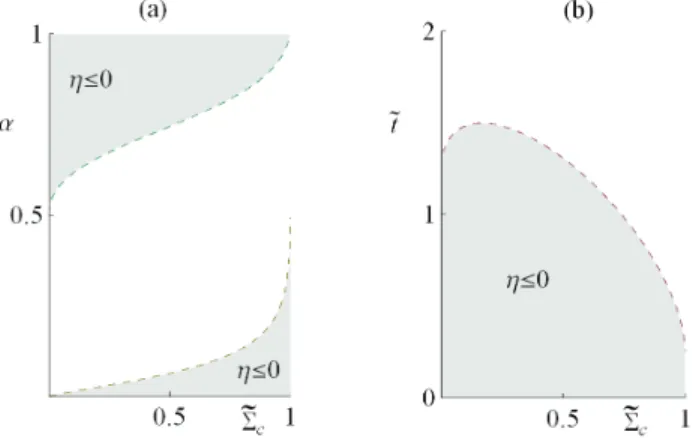
In [41], the region of physical interest in the LD model under maximum power conditions was analyzed. Then, as long as there is a heat leak in the device, the internal hot reservoir cannot reach equilibrium with the external hot reservoir, and the reversible configuration is not achievable.
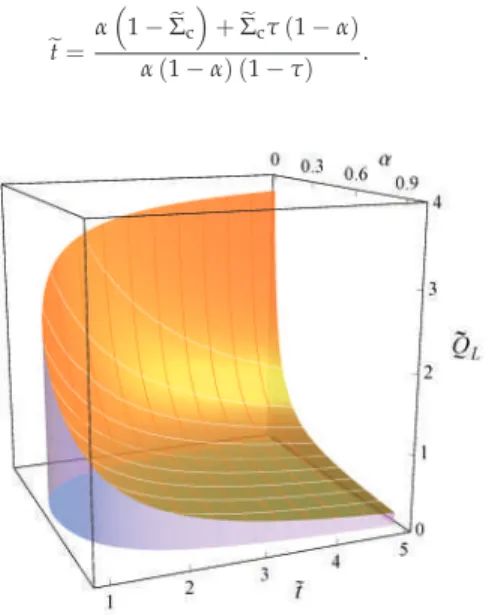
Maximum-Power Regime
It is well known that, for the Newtonian heat transfer law (k=1),ηPmax =ηCA is independent of theσhc value. Another incompatibility of the two approaches occurs in the Newtonian heat exchange (k =1): meanwhile, the Carnot-like scheme ηCA is independent of any value of σhc, and, in terms of the LD model, ηCA is strictly attached to a symmetric dissipationΣc=1/2(=Σh).

Conclusions
Irreversibilities and efficiencies at maximum power of heat engines: The illustrative case of a thermoelectric generator. Phys. Constitutive relation for nonlinear response and universality of efficiency at maximum power for tight-coupled heat engines. Phys.
The History and Perspectives of Efficiency at Maximum Power of the Carnot Engine
- Introduction
- Finite Time Thermodynamics
- Steady-State Modelling 1. Heat Transfer Conductance Model
- Transient Modelling
- Conclusions and Perspectives
This proves that the Carnot efficiency is the upper bound on the efficiency of the adiabatic and reversible system (two thermostats and the converter). All the previous results are related to the linear form of the heat transfer law (equation (10)).
![Figure 1. Extract from Moutier’s book [6] (p. 62).](https://thumb-ap.123doks.com/thumbv2/1libvncom/9201594.0/23.723.196.529.526.767/figure-extract-from-moutier-s-book-p.webp)
Global Efficiency of Heat Engines and Heat Pumps with Non-Linear Boundary Conditions
Method
This approach is proposed in Öhman [6] for comparing the global energy efficiency of different real heat engines. For the correlation of global energy efficiency of a real heat engine, it is possible to define a "Fraction of Carnot" (FoC) from Equation (6).
Results
Evaluation of heat pump systems can be made in a similar way to the above by defining Equation (9) as a fraction of Carnot for real heat pumps. The approach of the maximum power cycle, Integrated Local Carnot efficiency and Fraction of Carnot are useful in such studies.
Discussion
QCA Curzon–Ahlborn rate of heat transferred from the hot flow W αH, αL Inverse apparent heat capacity of hot and cold flow K/W. CpH,CpL Constant, linear specific heat capacity of hot and cold flow J/kg·K C(T) Non-constant, complex specific heat capacity J/kg·K.
What Is the Real Clausius Statement of the Second Law of Thermodynamics?
Misunderstanding of the Clausius Statement 1. Carnot’s Theorem
Clausius pointed out that the second law of thermodynamics in his mechanical theory of heat is called the theorem of equivalence of transformations. Therefore, the true Clausius statement of the second law should be the equivalence theorem of transformations. The theorem on equivalence of transformations is a basic theory of classical thermodynamics and it is necessary to be fully aware of it.
In the next section, we will see that Clausius' equality/inequality and the concept of entropy were derived from the equivalence theorem of transformations [24].
Alternative Mathematic Expression of the Second Law 1. Clausius Equality / Inequality and Entropy
So the sum of the equivalence values of all transformations in a reversible cycle must be zero. Fortunately, Clausius identified the Carnot function and further obtained the thermal efficiency of a Carnot cycle in terms of the equivalence of transformations theorem. For a Carnot cycle with two different heat source temperatures, the thermal efficiency can also be derived directly from the equivalence of the transformations theorem.
Therefore, it can perhaps be perceived as an alternative mathematical expression of the second law of thermodynamics.

Conclusions
Fenn, J.B. Engines, Energy and Entropy: An Introduction to Thermodynamics (Global View); Freeman: New York, NY, USA, 1982; pp. The efficiency of compressor heat pumps and refrigerators comes from the second law of thermodynamics. Int.
Performance of a Simple Energetic-Converting Reaction Model Using Linear Irreversible
The Model
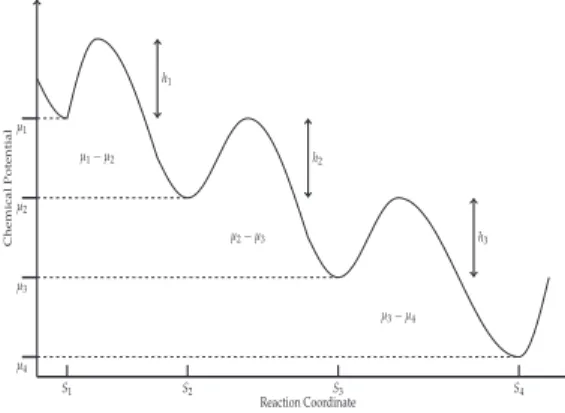
In the classical equations of chemical kinetics, which are known to describe a chemical process quite accurately, reaction rates are proportional to concentrations. Thus, this energy may be different for the different stages of the enzymatic reaction, causing the phenomenological coefficients to be different, and the degree of coupling qi to be different in each stage as well, which affects the thermodynamic properties of the system (e.g. power output or entropy production). Furthermore, Figure 2 shows the efficiency plotted as a function of the stoichiometric coefficient for different values of q.
Optimal operating regimes in the context of linear irreversible thermodynamics. A very interesting problem in many biological systems is the transfer of energy, which is essential.
Optimal Operation Regimes in the Context of the Linear Irreversible Thermodynamics A very interesting problem in many biological systems is the transfer of energy which is of decisive
In the context of linear irreversible thermodynamics, the efficient power function takes the form, . In the context of linear irreversible thermodynamics, the latter is interesting in the sense that we can compare not only the power output but also the cycle efficiency. Characteristic functions (P Maximum Power Output (MPO), Maximum Ecological Function (MEF) and PeMaximum Efficient Power Function (MEPF)) as a function of efficiency.
Later shows how important the parameter q is as it reflects the behavior of the irreversibilities in the system (see Figure 5-7).

Concluding Remarks
We can observe how the Power Efficient Function produces loop-like curves as seen in real heat engines. Now, from equations and (35), it is clear that the efficiency that maximizes some of the characteristic functions is related only to q, so in the end, the thermodynamic properties are related to the degree of coupling providing the basis for comparing different types of coupling in a two-flow system. Efficiency at peak power: A solvable analytical model for stochastic heat engines. EPL (Europhys. Lett.
Timed rate controller: optimal efficiency for maximum power output in physical and biological systems. Am.
Progress in Carnot and Chambadal Modeling of Thermomechanical Engine by Considering Entropy
The Chambadal Engine
The temperature difference of the source and sink levels, ΔTS, compared to the cyclic liquid level, ΔTCF, which remains the same, is also relevant for the heat input in the two cases. When the source has a finite heat capacity, there is a temperature variation of the primary fluid in the associated heat exchanger. By following several assumptions one can consider:. i) the presence of Novikov's degree of irreversibility [9], which is expressed by:.
Influence of the working fluid properties on optimized power of an irreversible finite dimensions Carnot engine.Energy Convers.
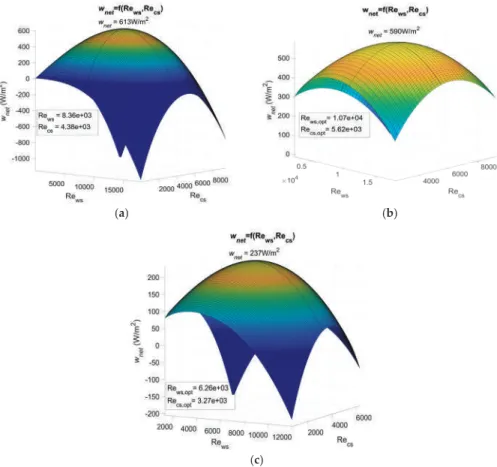
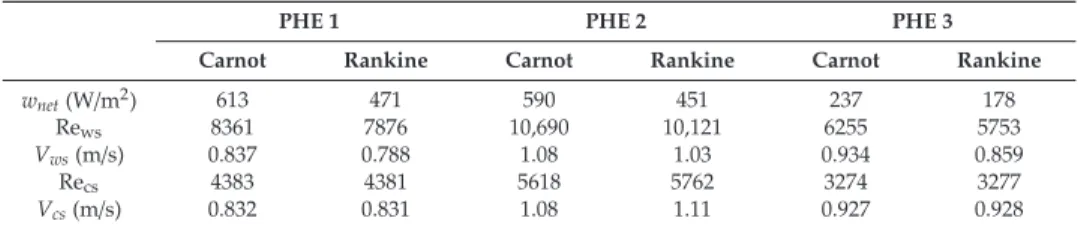
OTEC Maximum Net Power Output Using Carnot Cycle and Application to Simplify Heat
Exchanger Selection
Description and Analysis
In this study, the comparison of the heat exchangers is based on the net power supplied by the plant per unit of heat exchanger surface. Part of the gross power generated by the power plant is used for water pipes. The heat transfer coefficient of the working fluid is much greater than that of seawater, as the working fluid undergoes a phase change [24].
It was assumed that the working fluid at the exit from the heat exchangers is in a saturated state.
Optimization Process
In addition, Uehara and Ikegami showed a 44% reduction in the net power output of an OTEC plant for the same temperature change [23]. As for the Carnot cycle, the results for the Rankine cycle show that the temperature change will significantly affect the maximum net power output of the OTEC plant. An objective function of the net power output per unit area of the heat exchanger was defined for the Carnot and Rankine cycles.
The evolution of the output power as a function of the temperature difference was found to follow the same trends as found in other studies.

Energy and Exergy Evaluation of a Two-Stage Axial Vapour Compressor on the LNG Carrier
- Description and Characteristics of the Analyzed Two-Stage Compressor
- Measuring Equipment and Measuring Results
- Thermodynamic Efficiency Analysis
- Energy and Exergy Analysis Results and Discussion
- Variation and Optimization of Temperature at the Compressor’s Second Stage Inlet
- Conclusions
The schematic overview of the two-stage compressor is shown in Figure 1, where p1,t1 is the LNG vapor pressure and temperature at the compressor inlet to the first stage. The energy efficiency of the first stage compressor is higher than that of the second stage and averages around 52%. The exergy efficiency is smoothly increased throughout the range for the second stage of the compressor.
The energy efficiency of the two-phase compressor in the observed range, in the beginning, is 50.7%.

Second Law Analysis for the Experimental
Performances of a Cold Heat Exchanger of a Stirling Refrigeration Machine
Experimental Setup
The displacement piston function is to displace the gas between the hot and cold parts of the machine. The function of the regenerator is to store the heat from the liquid during one of the isochoric transformations of the cycle and to restore it in the other. The lower part of the machine, called the bounce space, contains the connecting rods and the crankshaft.
The main design parameters of the machine are: medium pressure between 15 and 20 bar, nitrogen as the working gas, stainless steel for the cold head and aluminum for the radiator on the hot sink (Table 1).
Mathematical Model
The other fluid is the working gas (Nitrogen) of the Stirling refrigerator and it flows alternately (corresponding to the rotation frequency of the machine) at constant temperatureTC in the inner tube corresponding to the cylinder of the machine (Labels 8 and 10). In this work, the heat capacity rate is the product of the mass flow rate and the specific heat capacity rate of the incompressible fluid. The complex flow field created by the internal geometry of the heat exchanger affects the pressure gradient required to drive the flow.
The two constants sa and b depend on the properties of the fluid, the flow regime and the geometric constraints of the heat exchanger.
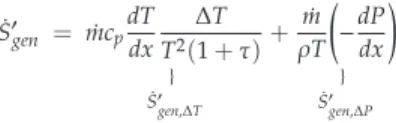
Results and Discussion
The entropy generation number (NS) increases with the length L of the heat exchanger due to the increase in fluid friction and pressure drop. For each mass flow rate ˙m of the refrigerant liquid, we measured the temperature TC of the cold gas in the expansion chamber of the refrigerator. The heat transfer affects the rate of entropy generation NS, which logically decreases with temperature TC, and the hydraulic diameter Dh, which corresponds to the dominance of the heat transfer irreversibilities over fluid losses (Figure 12).
The cold heat exchanger transfers heat from a gas to a coolant in the temperature range (240–300 K), and the efficiency of this operation is a result of the competition between heat transfer and irreversibilities in the fluid flow.

MDPI