111 5.14 Concentration profiles for different values of the Casson parameter and mag-. of the thermal and soluble slip factors. 197 8.11 Plot of the skin friction coefficient against transverse coordinate for different . values of the Casson parameter.
Numerical methods for differential equations in fluid flow
- Discretization methods
- The Runge-Kutta methods
- The bvp4c algorithm
- The quasi-linearization method (QLM)
- The successive linearization method (SLM)
- The Keller-box method
- The shooting Method
- Spectral methods
- The Adomian decomposition method (ADM)
- The variational iteration method (VIM)
- The differential transform method (DTM)
- Overview of numerical methods for fluid flow
The collocation points are the zeros of the polynomial chosen for approximation (Moulla et al., 2012). The advantage of the method is that it converges to exact solutions (Pue-On and Viriyapong, 2012) and requires fewer calculations than traditional discretization methods (Ali and Al-Saif, 2008).
Background on physical properties in fluid flow
- Fluid flow on exponential stretching/shrinking sheet
- Radiation effects in fluid flow
- Magnetohydrodynamics
- Viscous dissipation
- Free or Natural convection
- Fluid flow geometry
- Porous media
- Chemical reaction effects
- Partial slip effects
- Cross diffusion effects
- Double dispersion effects
In fluid flow, it is sometimes important to consider the effect of viscous dissipation (Jambal et al., 2005). The effect of natural convection in fluid flow is considered in this thesis because of its.
Objectives
The effects of double dispersion in fluid flow were studied by, among others, Loh and Vesudevan (2013) who investigated dispersion behavior in non-porous silica monolith. 2012) considered enhanced dispersion in supercritical fluids. 2010) investigated gas distribution in a multi-fan bioreactor. The effect of double distribution will be considered in Chapter 8. (See Appendix F). e) the local linearization method (LLM) applied with collocation to PDEs and (SQLM) applied with collocation to ODEs.
Thesis outline
In Chapter 6 we use the local linearization method (LLM) and Matlab bvp4c to solve a problem on radiation effects in MHD-free convection of a Casson fluid from a horizontal circular cylinder with partial slip in porous non-Darcy medium with viscous dissipation. In Chapter 8 we use the local linearization method (LLM) to solve a problem on double dispersion effects in Casson fluid flow with viscous dissipation and convective boundary conditions.
Review of the Matlab bvp4c solver
Strengths and weaknesses of the bvp4c solver
The quality of the initial guess can be critical to the performance of the solver, reducing or increasing runtime. The accuracy and convergence of the Matlab bvp4c algorithm depends on a good initial guess and works better for comparisons involving a few comparisons (Sibanda et al.,2012).
Successive linearization method (SLM)
We seek an approximate solution by solving the linear part of the equation under the assumption that ui and its derivatives are small. If ui(x) is a solution of Eq. 2.11), we let ui(x) denote the solution of the linearized version of Eq. 2.11) using the Taylor series and neglecting the higher order terms it gives. 2.12) can be solved by any numerical method.
Strengths and weaknesses of the successive linearization method (SLM)(SLM)
Spectral relaxation method (SRM)
To implement the spectral collocation method, we define the differentiation matrix. is the vector function of the collocation points and higher order derivatives are obtained in powers of D given by. We then apply the Chebyshev pseudo-spectral method to the iteration scheme shown in Eqs. 2.32) and the boundary conditions, we obtain the iteration scheme of the spectral Gauss-Seidel relaxation method, given by.
Review of the quasi-linearization method (QLM)
Following Motsa and Sibanda (2013), we assume that the true solution of Eq. 2.36) isyα(x) and thatyγ(x) is an initial approximation sufficiently close to toyα(x). In this thesis, we demonstrate the power of the spectral method and use the Chebyshev spectral collocation method (Makanda et al., 2013; Makanda et al., 2014b; Motsa and Sibanda, 2013).
Strengths and weaknesses of the quasi-linearization method (QLM)(QLM)
At this stage, the iterative scheme can be used with any method such as finite differences, finite elements and spline collocation method.
Bivariate quasi-linearization method (BQLM)
Assuming that the difference vr+1−vr and all its derivatives are small, we first approximate the non-linear operatorG by linear terms of the Taylor series or linearization by the QLM due to Bellman and Kalaba (1965), use. The values of the time derivatives at the Chebyshev-Gauss-Lobatto points (xi, tj) are calculated as
Strengths and weaknesses of the BSQLM
Introduction
Review of literature on fluid flow on exponentially stretching sheet
Bidin and Nazar (2009) studied the boundary layer flow over an exponentially stretching sheet with thermal radiation. Reddy and Reddy (2011) investigated the effect of thermal radiation on magnetohydrodynamic flow due to an exponentially stretching plate.
Mathematical formulation of fluid flow on an exponentially stretching sheetstretching sheet
In this chapter we investigate the effects of magnetic, radiative, and viscous dissipation parameters on the fluid flow and heat transfer characteristics of an exponentially stretching plate. Here the subscripts w, ∞ refer to the stretching surface and free flow conditions respectively, T0 and C0 are positive constants, U0 is the characteristic fluid velocity and L is the characteristic length of the stretching surface.
Skin friction, heat and mass transfer coefficients
We have calculated the important technical parameters, namely skin friction, heat transfer and mass transfer coefficients.
Analytical solutions for the momentum, heat and mass transfer equationsequations
To find the analytical solution for the heat transfer Eq. 3.12) we use the zeroth-order approximations of f and fη given by equation equation. The complementary solution of Eq. 3.35) is obtained in terms of confluent hypergeometric function in the following form.
Numerical solution procedure
In this chapter we used the shooting technique with the Runge-Kutta-Fehlberg scheme to determine two more unknowns and thus convert the boundary value problem into an initial value problem. After all six initial conditions were determined, the resulting differential equations were integrated using an initial value solver.
Results and discussion
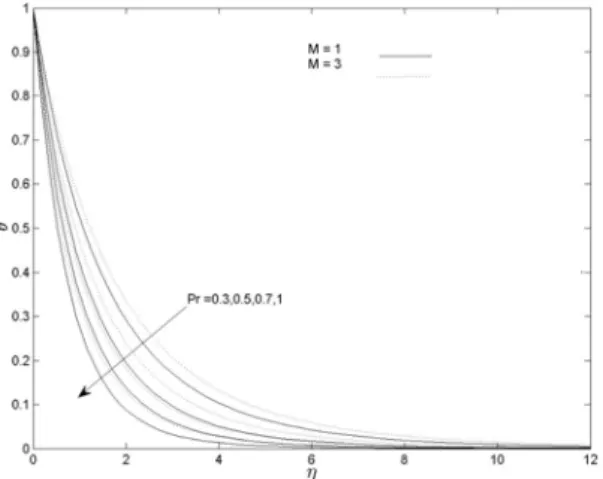
It can be seen that the increase of the magnetic parameter M results in the decrease of the mass transfer coefficient while. It is observed that increasing the values of M results in the thickening of the boundary layer of the species.
Summary
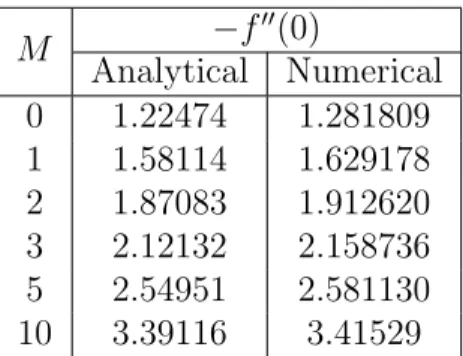
More accurate numerical solutions were observed in the energy equation of the problem than in the momentum equation. The numerical solution of the problem was compared with the solutions available in the literature and found to be in excellent agreement.
Introduction
Review of literature on fluid flow from a cone in viscoelastic fluid
Chen (2010) studied fluid flow in viscoelastic fluid with energy dissipation; Hsiao (2012) investigated viscoelastic fluid flow with viscous dissipation. These aspects will be considered in the formulation of the problem of fluid flow by natural convection from a cone in viscoelastic fluid.
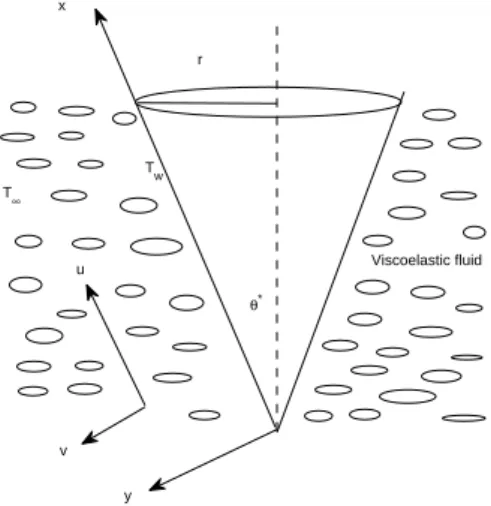
Mathematical formulation of fluid flow from a cone in viscoelastic fluidfluid
These boundary conditions take into account the linear surface temperature and no-slip conditions on the surface of the cone. The free stream conditions are considered to be at a lower temperature than at the surface of the cone.
Skin friction and heat transfer coefficients
Therefore we now derive the important fluid parameters which are skin friction and heat transfer coefficients. We have derived the important parameters, skin friction and heat transfer coefficients, so now we solve the governing equations numerically.
Numerical solution procedure
To overcome this problem, the system is decomposed into zero, first and second order systems by the viscoelastic parameter. For this purpose, we apply the successive linearization method to the systems of the resulting differential equations, which does not require small parameters as discussed in section 1.1.5.
Results and discussion
In Figure 4.13, the increase of viscoelastic parameter decreases the heat transfer coefficient and the increase of the Eckert number decreases the heat transfer coefficient. In Figure 4.15, increasing the viscoelastic parameter decreases the heat transfer coefficient and increasing the Prandtl number increases the heat transfer coefficient.
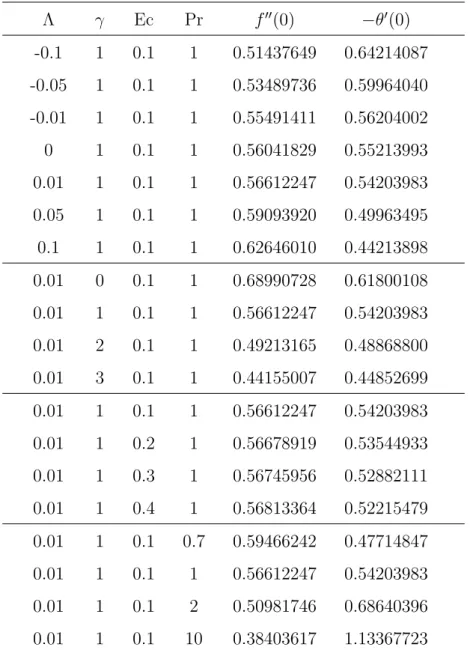
Summary
The graphs in Figures and 4.15 all show that increasing the viscoelastic parameter reduces the heat transfer coefficient. We also note that the heat transfer coefficient decreases with increased values of the permeability parameter (Figure 4.11) and the Eckert number (Figure 4.13), but that increasing the Prandtl number increases the heat transfer coefficient (Figure 4.15).
Introduction
Review of literature on Casson fluid flow over a stretching sheet
Dispersion of chemically reactive species in Casson fluid flow over an unstable stretching surface in porous medium. One of the most important applications of Casson fluid flow is the study of blood flow.
Mathematical formulation of Casson fluid flow over a stretching sheetsheet
Skin friction, heat transfer and mass transfer coefficients
Results and discussion
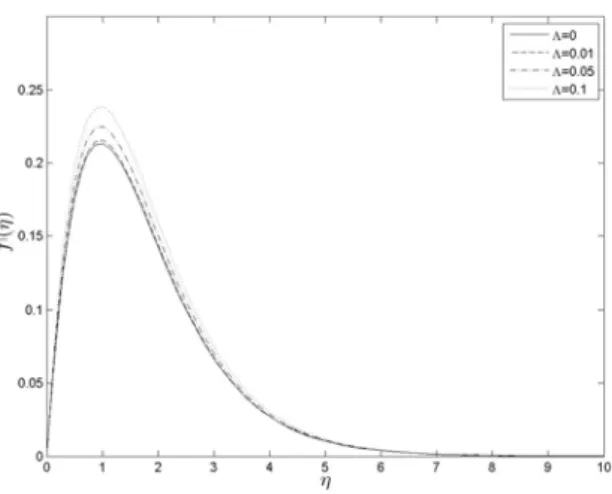
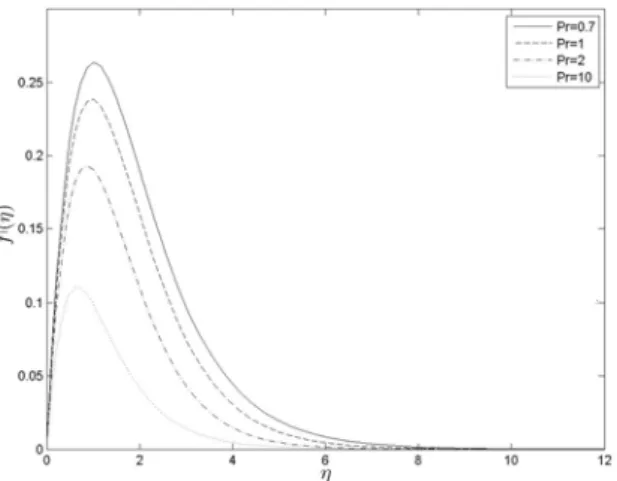
It can be seen from Figure 5.2 that increasing the Casson parameter (the fluid behaves Newtonian as the Casson parameter becomes large) results in decreasing velocity profiles. It can be seen from Figure 5.8 that increasing the Prandtl number P r results in decreasing temperature profiles.
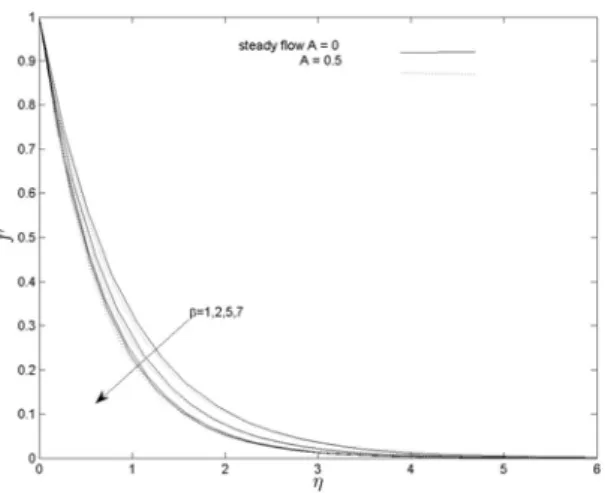
Summary
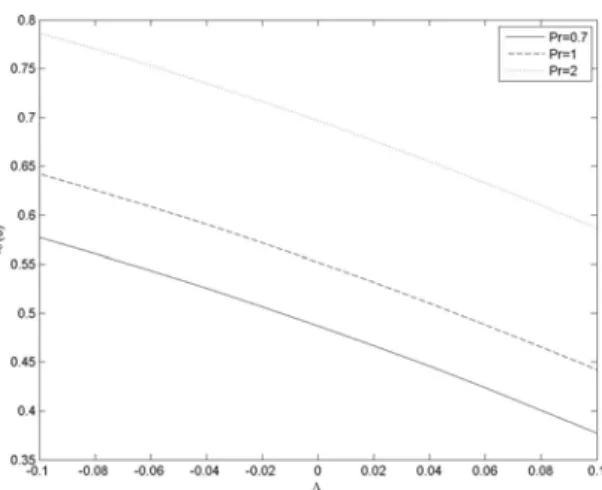
The variation of mass transfer coefficient related to −φ0(0) versus the instability parameter A for different values of the Casson parameter β and permeability parameter γ is shown in Figures 5.24 and 5.25. It can be seen from Figure 5.24 that increasing the Casson parameter decreases the mass transfer coefficient.
Introduction
Review of literature on Casson fluid flow from a horizontal cylinder
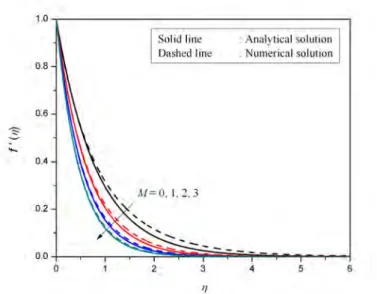
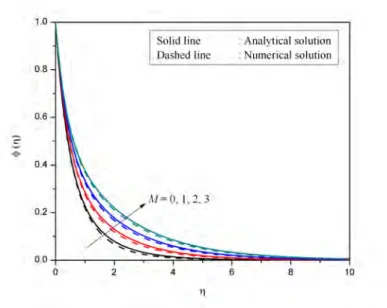
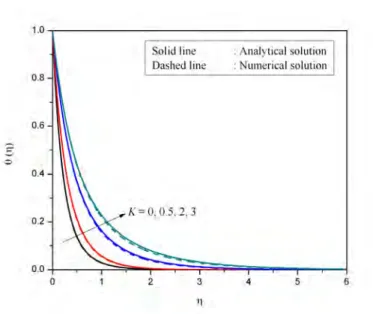
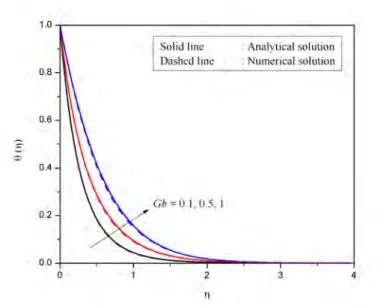
Effects of radiation on MHD free convection of Casson fluid from a horizontal circular cylinder with partial. It is therefore important to study the fluid flow in Casson fluid with partial slip conditions.
Mathematical formulation of Casson fluid from a horizontal cylindercylinder
Newtonian model, μB is the dynamic plastic viscosity of the non-Newtonian fluid, Py is the fluid yield stress. The Rosseland approximation for radiation can be written as follows; where σ∗ is the Stefan-Boltzman constant and k∗ is the absorption coefficient.
Skin friction and heat transfer coefficients
We then derive expressions for important technical parameters, which are skin friction and heat transfer coefficients. The heat transfer from the surface of the circle to the liquid is given by
Numerical solution procedure
In this section, we describe the implementation of the local linearization variant of the quasi-linearization. The derivatives with respect to η are defined in terms of the Chebyshev differentiation matrix as.
Results and discussion
The variation of the radiation parameter K on velocity profiles for different values of the velocity slip factor Sf as shown in Figure 6.4. The variation of the radiation parameter K on temperature profiles for different values of the thermal slip factor as shown in Figure 6.7.

Summary
It can be seen from the figure that an increase in the thermal slip factor ST results in an increase in the heat transfer coefficient. Increasing the radiation parameter K decreases the heat transfer coefficient; this is expected because increasing the radiation parameter would have the effect of increasing the liquid temperature.
Introduction
Review of literature on Casson fluid from a spinning cone
The thermophoretic force due to temperature gradients causes the movement of the solute in the fluid flow regime. In this chapter, we discuss the effects of radiation, viscous dissipation, porous media, and Casson fluid flow, which were discussed in Chapters 4, 5, and 6.
Mathematical formulation of Casson fluid flow from a spinning conecone
Velocity, rotational, thermal and solution slip factors are taken into account on the surface of the cone. 2πc/Py is the non-Newtonian Casson parameter, α =k/ρCp is the thermal diffusivity, k is the thermal conductivity of the liquid, qr is the radiant heat flux.
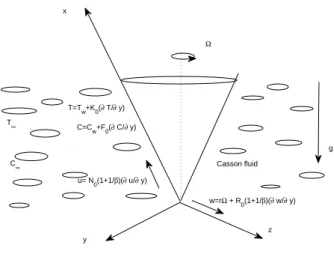
Skin friction, heat transfer and mass transfer coefficients
We are now ready to describe the numerical solution procedure for the problem of numerical analysis of free convection Casson fluid flow from a rotating cone in non-Darcy porous medium with radiation, partial slip and cross-diffusion, and viscous dissipation effects.
Numerical solution procedure
Improving the convergence of the spectral relaxation method (SRM)(SRM)
In Figure 7.2, the spectral relaxation method (SRM) error decreases with the increasing number of iterations, which shows the accuracy of the spectral relaxation method (SRM).
Results and discussion
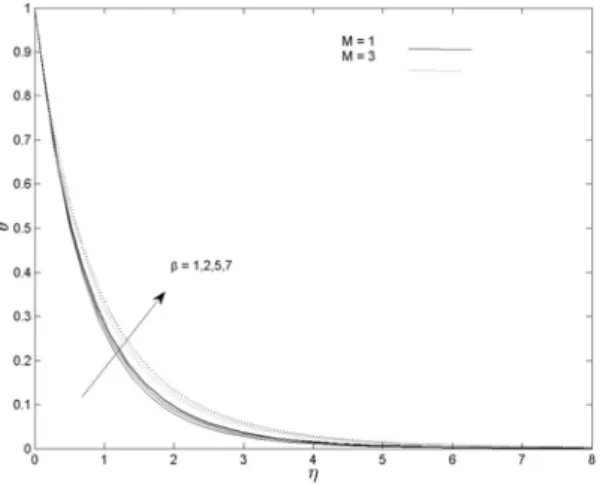
Increasing the concentration slip factor Sco results in increasing the heat transfer coefficient. From the figure it can be seen that increasing the Dufour number results in decreasing the mass transfer coefficient.

Summary
We therefore interpret an increase in the Dufour number as having the effect of increasing the energy flux that increases the solute concentration in the fluid regime, thereby reducing mass transfer to the fluid. In this chapter, we point out the new results on the effects of increasing rotation and solution slip factors that have not been previously reported in the literature.
Introduction
Review of literature on double dispersion on Casson fluid flow