getdoc6559. 262KB Jun 04 2011 12:04:27 AM
Teks penuh
Gambar
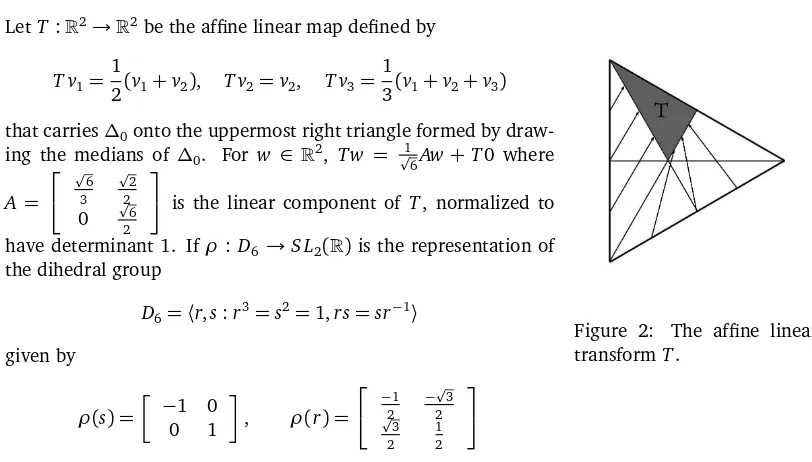
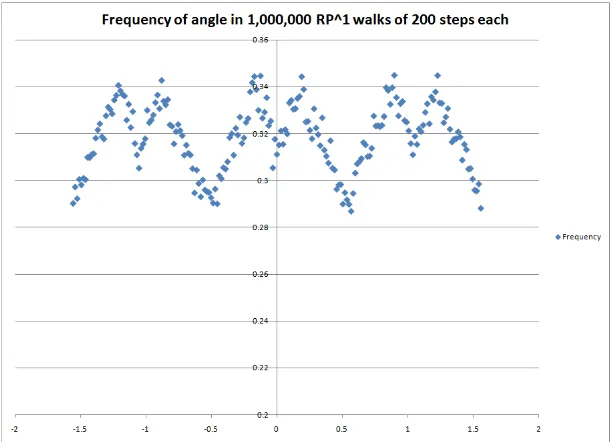
Garis besar
Dokumen terkait
Connections are made with an existing condition number for π T , and the results are applied to the class of Markov chains arising from a random walk on a tree..
, Laws of the iterated logarithm for the local times of recurrent ran- dom walks on Z 2 and of Levy processes and recurrent random walks in the domain of attraction of Cauchy
Recently much work has been done on the (simple or not) random walk on the unique infinite cluster for the supercritical (bond or site) percolation in Z d (see e.g.. Another
Dobrushin proved in his thesis [2] an important central limit theorem (CLT) for Markov chains in discrete time that are not necessarily homogeneous in time. Previously,
Keywords: Random Matrices, Block-Matrices, Limiting Spectral Measure, Circulant Block- Matrix, Semicircular Noncommutative Random
Keywords: General state space Markov chains; f -regularity; Markov chain central limit theo- rem; Drazin inverse; fundamental matrix; asymptotic
A question of increasing importance in the Markov chain Monte Carlo literature (Gelfand and Smith, 1990; Smith and Roberts, 1993) is the issue of geometric ergodicity of Markov
Central limit theorems for functionals of general state space Markov chains are of crucial importance in sensible implementation of Markov chain Monte Carlo algorithms as well as