vol18_pp126-145. 202KB Jun 04 2011 12:06:02 AM
Teks penuh
Gambar

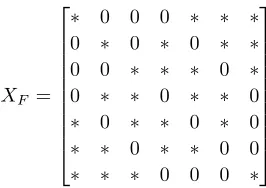
Garis besar
Dokumen terkait
The problem of finding the minimum rank (maximum nullity) of edge subdivisions of a given graph G is investigated.. Is is shown that if an edge is adjacent to a vertex of degree 1 or
Moreover, the minimum (resp. maximum) number of edges for all (connected) graphs with pendent vertices and nullity η are determined, and the extremal graphs are characterized..
The number of zero eigenvalues in the spectrum of the graph G is called its nullity and is denoted by η ( G ).. This question is of great interest in chemistry, because, as has
The minimum rank problem is the problem of finding the smallest rank of a matrix in the set of symmetric matrices having the zero-nonzero pattern of off-diagonal entries described by
Moreover, in any minimum rank problem whatsoever, we need not concern ourselves with any graphs in which two degree two vertices are adjacent, or a degree two vertex is adjacent to
In in- stances that the clique cover number broke down, we found a combination of cliques and clique-stars that yielded the minimum rank as well as the entire inertia set by
Minimum rank, Symmetric matrix, Finite field, Projective geometry, Polarity.. graph, Bilinear
Our second con- struction produces a ( −J )-type tournament matrix from two minimum rank tourna- ment matrices of even orders..