Mathematics authors titles recent submissions
Teks penuh
Gambar
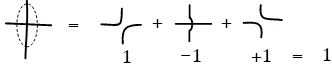
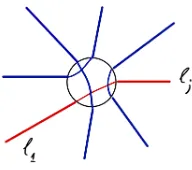
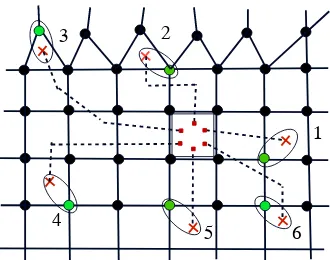
Garis besar
Dokumen terkait
To show that Jac(X) does not have complex multiplication, it suffices to exhibit an abelian subvariety without complex multiplication. A natural candidate for this is the jacobian
A bilinear form in the spirit of Kato’s proof for the Navier-Stokes equations is used, coupled with suitable estimates in Chemin-Lerner spaces.. In the one dimensional case, we
In the second part of the work, we derive some results valid for slice regular functions over finite- dimensional division algebras, which had not been proven with the original
The proofs of Lemma 15, Lemma 16 and the corresponding greedy-type heuristic suggest that weighted rep- resentations where all minimal winning coalitions have the same weight,
In this paper we describe a characterization for the Maaß space associated with the paramodular group of degree 2 and squarefree level N.. As an appli- cation we show that the
Meunier [25], by using his colorful theorem, generalized the Simonyi- Tardos lower bound [30] for the local chromatic number of Kneser graphs to the local chromatic number of
In Section 2 we provide the necessary preliminaries like a detailed definition of lifted maximum rank distance codes, acting symmetry groups, and upper bounds for code sizes based
This however does not give new metric spaces because, by the next lemma, a pseudometric space and its metric quotient have the same tight span..