Second, potential market power in the downstream market may be of concern to a benevolent government, which also happens to be the auctioneer. They investigate the effects of the second-price sealed bid auction (with a reserve price and an entry fee) on the downstream market. In this case, the government can act as a regulator and aim to maximize a combination of total surplus in the downstream market as well as auction revenue.
The first equation in (6a) is the company's profit in the downstream market, while the company's profit after subtracting the cost of the new spectrum is given in equation (6b). The right-hand side in equation (6a) is the sum of the profits from the high and low products, while the last term in equation (6b) is the cost of the new spectrum, which depends on the auction price Pa. In the rest of the article, we assume that the demand for both high and low products is linear, which makes the equilibrium for the capacity constraint Cournot model in the downstream market unique; see Laye and Laye (2008).
Therefore, unless it wins new spectrum at the auction, a company cannot produce in the market for new products. For example, suppose one company wins all the units at the auction, driving the other companies out of the market for new products. In this case, the company can operate in the market as a monopolist with the entire spectrum.
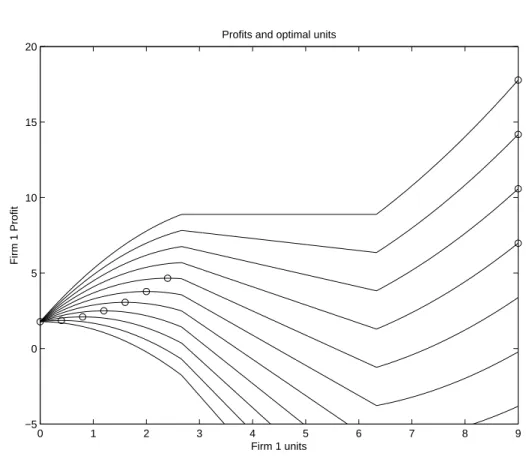
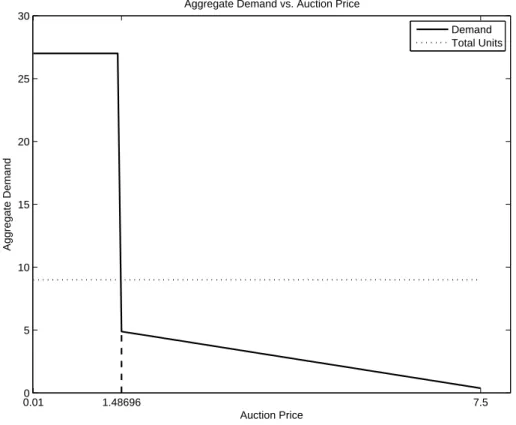
As expected, when the auction price is low, the firm wants to acquire all the units and become a monopolist in the market.
Solving the Auction: Rival Bidding
However, when the auction price reaches a certain threshold, it is no longer profitable. If companies' bids lead to excess demand, the auction will continue for at least one more round, during which the auction price will go up. Because the companies submit their bids at the same time, each auction bidding decision is essentially a Cournot game, with companies evaluating their own profits in both markets and deciding whether to bid more aggressively to limit production of the other companies' new product . market, or to provide what they need to produce optimally.
As a result, they can engage in mixed strategies, where they can assign a positive probability to go to a new round and close the auction at the current price, depending on the auction price. Offers that do not increase. In an hourly auction, bidders are often not allowed to raise their bids during the auction. This introduces a history dependency so that the last bids of firms from the last round are included in the set of state variables of the dynamic problem.
Successive declines in demand become important because in the event that demand falls below supply, firms that have reduced demand may be required to buy units of the good, if the terms of the auction state that there can be no excess supply. . A firm that initially fails to lower its demand can try again before the auction price rises. Given our solution for the downstream market and profit structure given in equations (6), we can calculate the payoffs that any firm receives at the end of the auction.
Suppose the vector Ba is the profit of the companies at the end of the auction. In addition, if we believe that the auction does not allow excess supply, we set an additional boundary condition at each time step that will immediately approve the auction as PM. The second is the expected payout for a company as a function of the company's current range of bids, the probability of falling demand, and the.
To calculate Viandπi, we proceed by backward induction, returning from the terminal (high) price of the auction. In equation (9), the continuation value is equal to the final value, unless there is excess demand at the current price, in which case the auction ends. Note that any reduction in demand results in the auction moving to a new level of demand and that the price remains at the same level, which allows for further reductions in demand.
Non-Rival Bidding
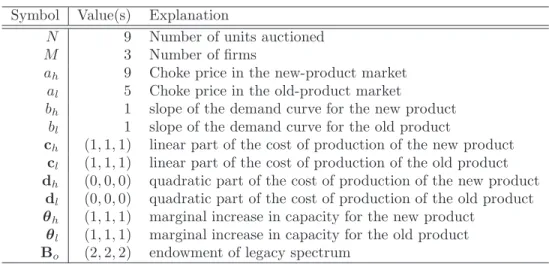
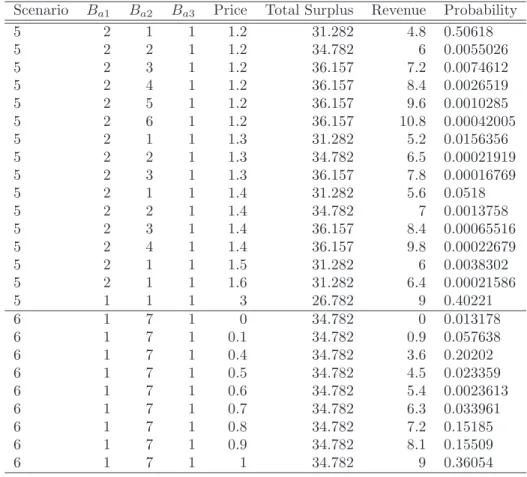
Each scenario is a slight variation of the benchmark model, which assumes parameter values from Table 1. When the auction price is low, the companies aim to win all the units to become a monopoly. Since the companies initially bid to be a monopolist, the auction ends at the price of $1.4227, after which each company can no longer afford to be a monopolist.
We perform comparative statistics on the marginal cost of production and the initial donation of the old spectrum. Since there is still an oversupply at the end of the auction in scenario 0, company 3 can simply claim more spectrum. The auction price rises in this scenario because Company 3 prefers to be a monopolist until the auction price reaches 1.4870.
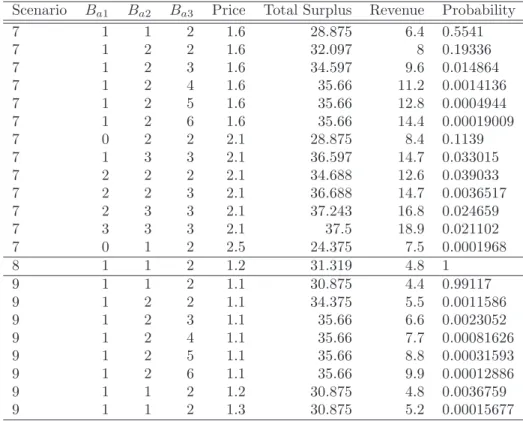
In scenario 4, where firm 3 has the lowest marginal cost across all scenarios (ch3 =cl3 = 0.1), the spectrum units acquired by firm 3 increase by almost 40 percent to 2.27 units compared to the standard model, and the auction price goes to almost $1.62. The auction price also drops to $1.4227, which is the same price as in scenario 0, due to the discretization of the auction price. In scenarios 7–9, we focus on the allocation of legacy spectrum, denoted Bl, and investigate how auction firms react if they have to use some of the new spectrum in the low-product market.
Higher demand for the new spectrum increases the auction price, leading to an increase in revenue compared to scenario 0. In scenarios 8 and 9, some of the firms (firms 1 and 2 in scenario 8 and firm 3 in scenario 9) have enough of the legacy spectrum to produce in the low product market. Nevertheless, we find that the firms do not use any of the new spectrum to produce the low product.
We interpret this result in the following way: if some firms have enough of the legacy spectrum, the inferior product market turns into a Stackelberg game rather than a Cournot game, since firms with enough spectrum can constrain others to produced at the same time. level as before. We calculate the auction price at which equilibrium offers change: either total demand decreases or the supply structure changes. As mentioned above, when the auction price is low, all firms aspire to be monopolists.
Rival Bidding
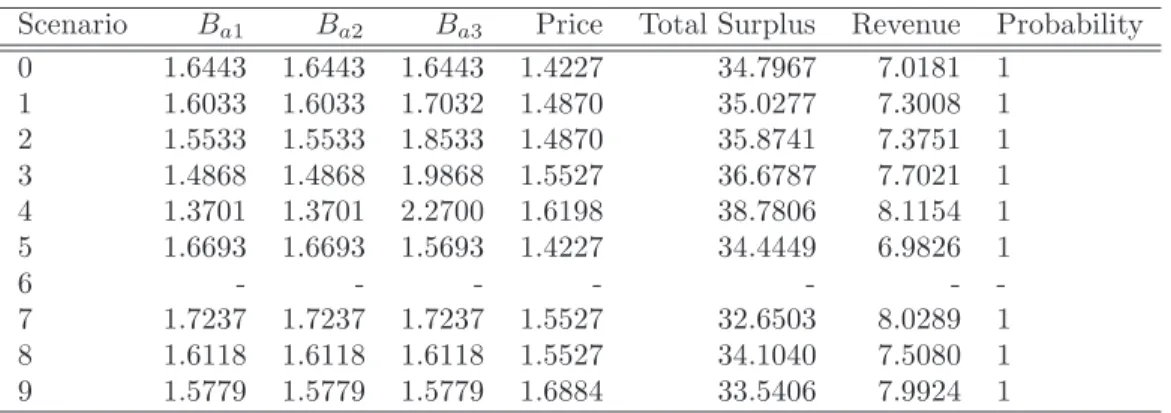
Given Company 3's lower marginal costs, it would make heavy use of the third unit of spectrum, resulting in significantly lower profits for Companies 1 and 2. An alternative scenario plays out if the first company to drop demand is followed by a of the other companies. falling demand, which each does with a 34.76 percent probability. Subsequent prices represent the companies' continued attempts to clear the market as the auction price becomes very high, culminating in some very costly outcomes where companies randomizing to see who remains as a monopolist in the market can own excess units of spectrum when the auction is released. .
Instead, one of the efficient firms gains the most units, and the other two become weaker competitors. Compared to scenario 0, all units are much more likely to be sold about 2 percent of the time. Also, just like in scenario 1, the established companies (with a lower value) have an incentive to raise the price, because they risk losing. of firm 3 expanding its activities in the low-use market.
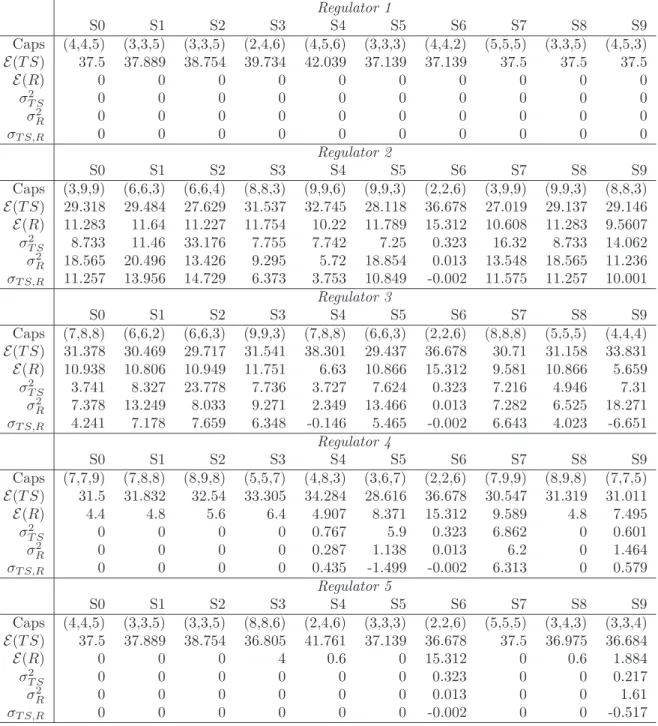
When two incumbents face a single entrant, the contender is able to buy a larger share of the new spectrum. In particular, the regulator may have a trade-off between auction revenue and total surplus. As a result, the regulator may decide to intervene in the auction by setting limits to regulate the maximum number of units that each firm can win in the auction.
The first two terms in equation (14) are the weighted average of the expected total surplus and income, and the last term is the variance of these. 5 A more libertarian view of the auction may note that the government's use of earned income may lead to a lower total surplus than would be achieved by using this income as profit for the private sector. For all our scenarios considered here, since the optimal strategy when maximizing total surplus leads to a collapse of the auction (see Table 8), a regulator with this view will choose the same cap structure as a regulator that purely with total surplus is concerned.
In contrast, as firm 3 becomes more efficient (in scenarios 3 and 4), regulator 5 is willing to let the auction run by giving a more generous cap to the efficient firm and one of the less efficient firms. Winning large volumes in the auction will allow a participant to exercise significant power in the downstream market. We show that market participants who make less efficient use of spectrum (either because of higher marginal costs or have large existing positions) have strong incentives to hold up the market and drive up prices with the aim of reducing other firms' positions in the market.
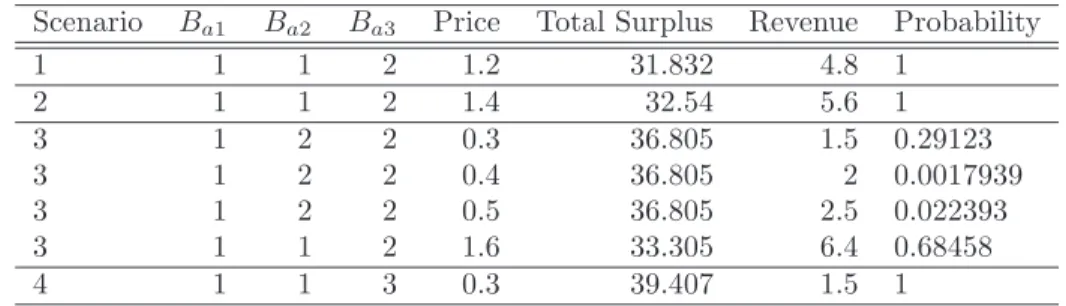
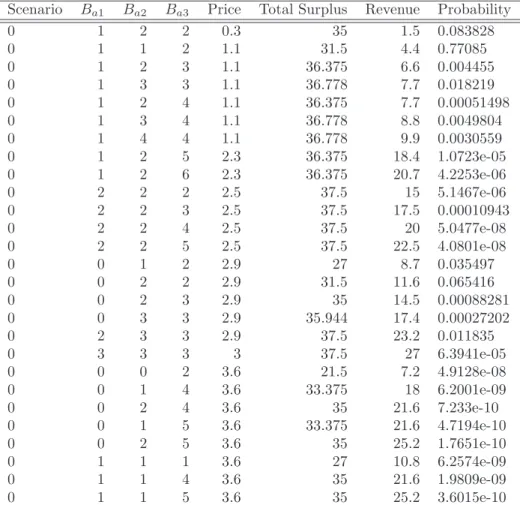
Mechanism Choice and Strategic Bidding in Divisible Good Auctions: An Empirical Analysis of the Turkish Treasury Auction Market. Columns represent (in order) allocations to the three firms, price for the equilibrium in question, social welfare, revenue, and finally the probability of the equilibrium occurring. As a result, this case exhibits many equilibria, ranging from an early clearing of the market in which a competitor receives a small share to a high-earnings scenario in which all spectrum is purchased.
For each regulator, we show the coverage structure (Caps), expected total profit (TS), expected revenue (RA) and the covariances of the variables.