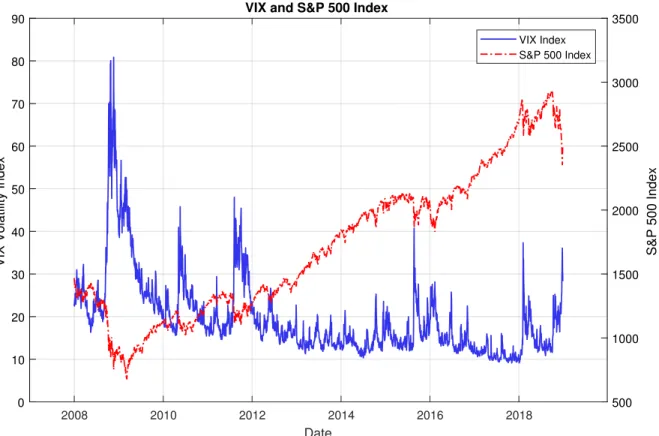
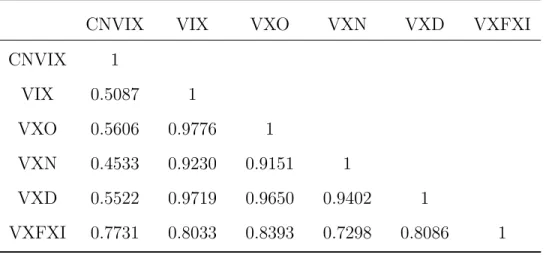
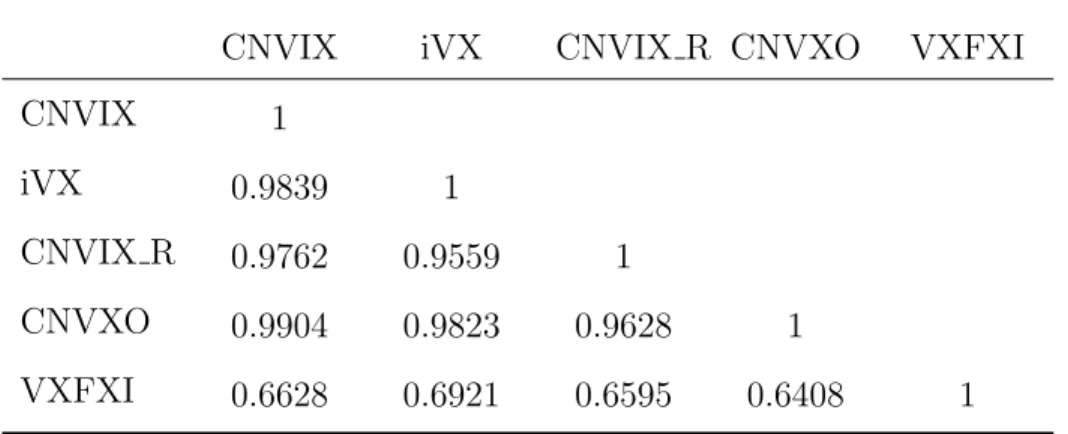
In CNVIX, we find a strong negative effect of asymmetric leverage and a positive mean volatility risk premium (VRP) that can predict the underlying return of the SSE 50 ETF over a monthly period. In 2003, the CBOE updated the VIX methodology in the CBOE (2003) VIX White Paper, which describes a new model-free VIX based on S&P 500 option portfolios following the pioneering work of Breedn and Litzenberger (1978), Demeterfi et al. Most of the blue chip stocks in the FXI ETF are cross-listed on the HKEX and SSE, Table 1 reports the top 10 stocks in both the FXI ETF and the SSE 50 ETF, 6 of the top 10 weighted stocks are cross-listed on both exchanges. 3 The asymmetry of information, media coverage and trading rules between investors in Mainland China and Hong Kong has often resulted in a discount/premium for listed stocks (Chakravarty et al., 1998; Ding et al., 2018 and Yuan et al., 2018 . etc.).
We use the standard SHIBOR term structure to interpolate the risk-free rate corresponding to each option's maturity each day.4 The implied future price is derived from the put-call parity using the At-The-Money option pair ( ATM). where ATM is defined as the strike price where the bid and call prices are closest. For each option term in the SSE 50 ETF, the average number of strikes is only about 10%/30% of the average number of SPX/FXI option strikes, which the CBOE uses in calculating the VIX/VXFXI index.
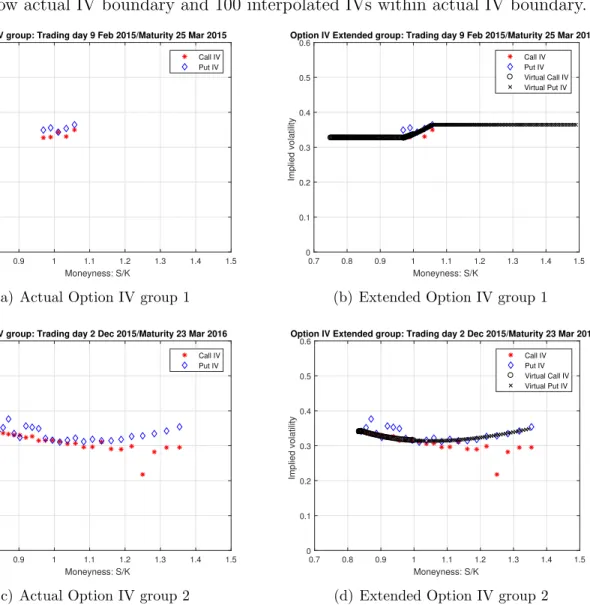
Smooth interpolation-extrapolation in the SSE 50 ETF op- tion market
Direct implementation of the CBOE (2003) methodology for calculating CNVIX with SSE 50 ETF options could result in large truncation and discretization errors since the number of strikes is so limited.9. lt; Please. 2013a) we create virtual possibilities within the actual stroke range (interpolation) and beyond the actual stroke range (extrapolation). For virtual option strikes within the range, we use the IV function proposed by Zhang and Xiang (2008) in Equation (8) to calculate the IV of virtual options, while for virtual option strikes exceeding the actual strike, we use the IV of actual options at the limit as these virtual options' IV.10 We create an additional 100 option clauses within the actual range of clauses and delete those virtual options which have the same clauses as the existing options.
We then use the monthly standard deviation of the SSE 50 ETF to determine the range for the additional 100 virtual shocks so that they cover eight standard deviations of the underlying asset returns. Whaley's (1993) methodology requires only 8 near-the-money options to calculate the volatility index, on some extreme volatile days, no near-the-money put or call options are available in the options chain, the index cannot be calculated on these day.
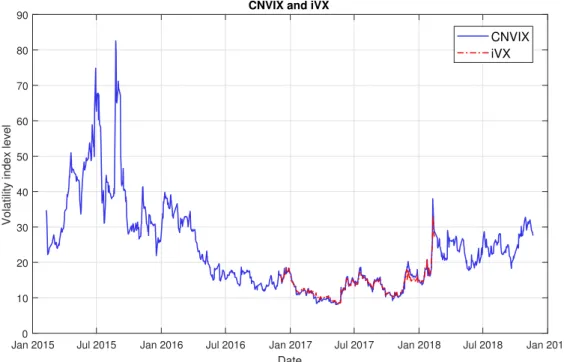
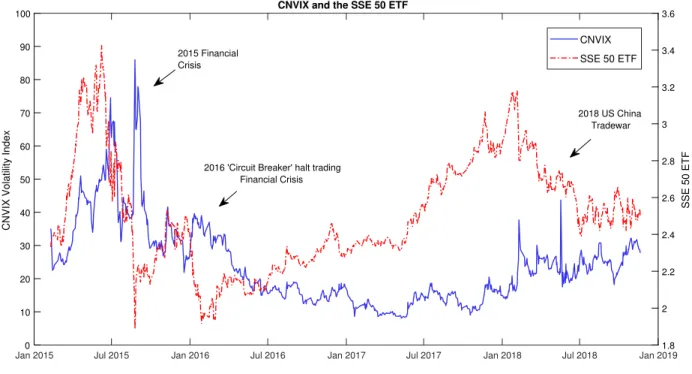
Relationship of the CNVIX with the underlying market
As investors expect the stock to become more volatile as leverage increases, they close their position in the stock, which leads to asymmetric relationship between volatility and return. However, Schwert (1989) shows that leverage alone is not sufficient for the negative association with volatility. It has been documented in the previous literature that the volatility estimated by options exhibiting more pronounced asymmetry leverage effect (eg Bates, 2000, Whaley, 2000, Eraker, 2004 and Whaley, 2009).
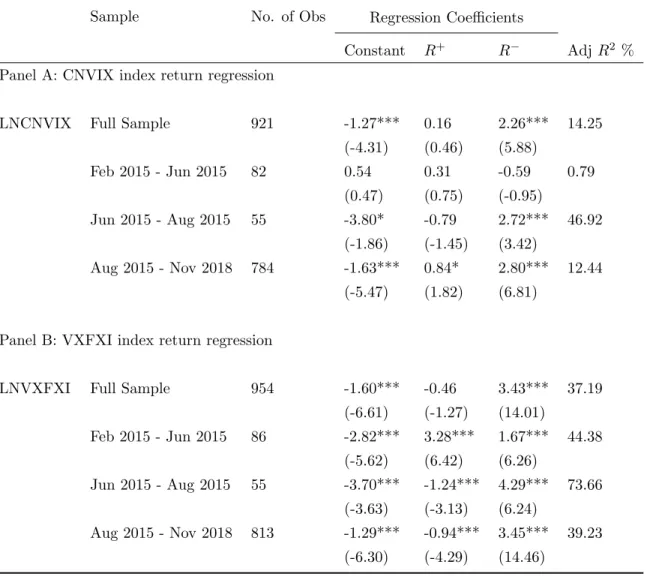
To document the time-series behavior of the leverage effect in the CN-VIX/VXFXI model-free volatility indices, we examine the volatility indices and their underlying return by splitting the positive and negative returns of their underlying asset. If the leverage effect existed in the model-free volatility indices, we should observe a negative/positive value of β1/β2, and in terms of an asymmetric relationship, β2 should be higher than β1. We would expect a volatility index to show a mean-reverting pattern that is stationary, but our sample is too short to capture a long volatility cycle.
1995) find that negative returns on the underlying asset are associated with greater changes in the index compared to positive returns. Although the positive β1 is insignificant in the full sample and is smaller than β2, it indicates that the underlying asset's negative return has a greater impact on volatility. We find that the index regression results show a similar leverage effect as the index return regression. They are available on request.
We have similar findings in panel B, when we model the volatility index with VXFXI. The return of the VXFXI index is negatively correlated with the underlying return, and the larger β2 coefficient of the negative return indicates the asymmetric leverage that also existed in VXFXI. The asymmetric effect of leverage is most pronounced for the fundamental return during the financial crisis in 2015.
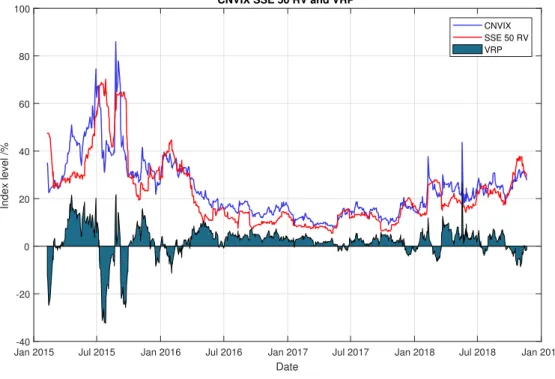
CNVIX-based VRP
We find that the average VRP of the SSE 50 is positive, which is consistent with the previous studies on the US options markets (e.g. Carr and Wu, 2008 and Bollerslev et al., 2009). To ensure that the prediction results are not affected by the model, we construct three control variables following Bali and Hovakimian (2009). First, the default spread (DFSP), which is defined by the difference in the return between the 1-year BBB China Bond Index rated corporate bond and the 1-year AAA China Bond Index rated corporate bond.
Second, the term spread (TERM), which is defined as the difference between the 10-year Chinese Treasury bond and one-month Treasury bill. Finally, the stochastically subtracted risk-free rate (RREL), which is defined as the yield of one-month China treasury bill minus its one-year backward moving average. Before the regression analysis, we test whether the time series of regressors are stationary or not.
VRP and return predictability
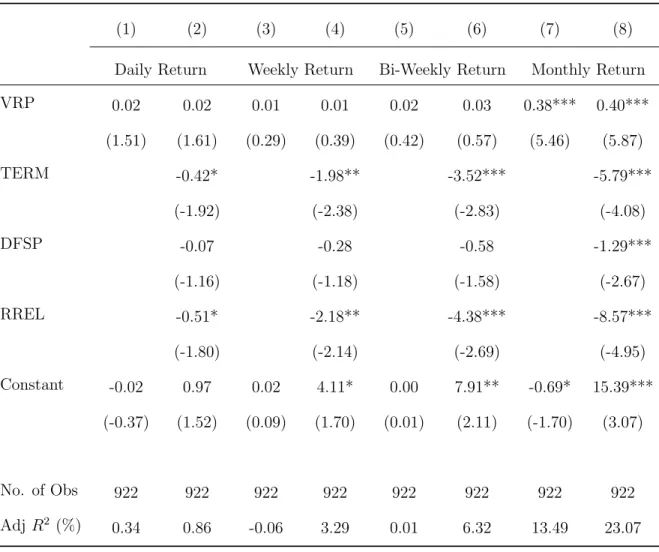
We present the results of the regression in equation (13) of the overlapping/non-overlapping future market return at different horizons in Table 8 and 9. We find that the VRP can significantly predict the future monthly returns on the SSE 50 ETF, while used either overlapping or non-overlapping estimation windows. Column (8) in Table 8 and column (6) in Table 9 report the results after adding the control variables.
We also run BS model volatility index CNVXO-based VRP regression in Table 10 (overlapping) and Table 11 (non-overlapping). Although the BS model-based VRP has fewer observations due to availability of near-the-money options, the predictive power of VRP to future returns is similar to the model-free VRP, which is inconsistent with Bollerslev et al. 2009) finding that the BS model-based VRP has less predictability about the yield. From column (3)-(6) in Table 12, we find that VXFXI-based VRP has significant forecasting power over the weekly and biweekly forecasting horizon, but the coefficient is quite small.
VXFXI based VRP has no predictive power for overlapping future daily and monthly horizons. From columns (1) and (5) in Table 12, we see that on the non-overlapping future horizon VXFXI-based VRP has significant predictive power and results are consistent when we add control variables. In this article, we introduce the model-free volatility index in China, the CNVIX, based on the newly established SSE 50 ETF options market and analyze its characteristics from February 9, 2015 to November 20, 2018.
We interpolate/extrapolate the option data set with the IV function, which reduces truncation and discretization errors in the construction of the volatility index. Finally, we analyze the model-free and VRP based on the BS model in China. The results are consistent with previous literature on developed options markets, which confirmed that the model-free methodology is also applicable to emerging and less liquid options markets.
Interpolation/Extrapolation of option dataset
Bakshi, Gurdip and Nikunj Kapadia, 2003a, Delta hedges and the negative market volatility risk premium, Review of Financial Studies. Bekaert, Geert and Guojun Wu, 2000, Asymmetric Volatility and Risk in Stock Markets, Review of Financial Studies 13, 1–42. Black, Fischer and Myron Scholes, 1973, The pricing of options and corporate liabilities, Journal of Political Economy.
Bollerslev, Tim, George Tauchen and Hao Zhou, 2009, Expected Stock Returns and Variance Risk Premia, Review of Financial Studies. Bugge, Sebastian A, Haakon J Guttormsen, Peter Moln´ar and Martin Ringdal, 2016, Implied volatility index for the Norwegian stock market, International Review of Financial Analysis. Campbell, John Y, and Ludger Hentschel, 1992, No news is good news: An asymmetric model of changing volatility in stock returns, Journal of Financial Economics 31, 281–.
Chang, Bo Young, Peter Christoffersen, and Kris Jacobs, 2013a, Market Distortion Risk and the Cross Section of Stock Returns, Journal of Financial Economics 107, 46–68. Choi, Jaewon and Matthew Richardson, 2016, Volatility of a firm's assets and the leverage effect, Journal of Financial Economics. Christie, Andrew A, 1982, The stochastic behavior of common stock variances: Value, leverage, and interest rate effects, Journal of Financial Economics.
DeMiguel, Victor, Yuliya Plyakha, Raman Uppal, and Grigory Vilkov, 2013, Improving portfolio selection using option-implied volatility and bias, Journal of Financial and Quantitative Analysis. Ding, Rong, Wenxuan Hou, Yue Lucy Liu and John Ziyang Zhang, 2018, Media Censorship and Stock Price: Evidence from the Foreign Stock Discount in China, Journal of International Financial Markets, Institutions and Money. Fleming, Jeff, Barbara Ostdiek and Robert E Whaley, 1995, Predicting stock market volatility: A new measure, Journal of Futures Markets.
French, Kenneth R, G William Schwert, and Robert F Stambaugh, 1987, Expected Stock Returns and Volatility, Journal of Financial Economics 19, 3–29. Li, Jupeng, Xiaoli Yu, and Xingguo Luo, 2019b, Volatility Index and Return Volatility Link: Intraday Evidence from the Chinese Options Market, Journal of Futures Markets (forthcoming). Sensoy, Ahmet and John Omole, 2018, Implied volatility indices: A review and extension to the Turkish case, International Review of Financial Analysis.
Yuan, Di, Xiafei Zhou and Shan Li, 2018, Dynamics of financial market integration between Chinese A- and H-shares, Emerging Markets Finance and Trade.